鲸鱼优化算法在水库优化调度中的应用

崔东文

(云南省文山州水务局,云南 文山 663000)



鲸鱼优化算法在水库优化调度中的应用

崔东文

(云南省文山州水务局,云南 文山 663000)

为验证鲸鱼优化算法在水库优化调度求解中的可行性和有效性,采用4个典型测试函数对鲸鱼优化算法进行仿真验证,并与布谷鸟搜索算法、差分进化算法、混合蛙跳算法、 粒子群优化算法、萤火虫算法和SCE-UA算法共6种算法的仿真结果进行对比分析; 将鲸鱼优化算法与6种对比算法应用于某单一水库和某梯级水库中长期优化调度求解。结果表明:鲸鱼优化算法寻优精度高于其他6种算法8个数量级以上,具有收敛速度快、收敛精度高和极值寻优能力强等特点;鲸鱼优化算法单一水库和梯级水库优化调度结果均优于其他6种算法;鲸鱼优化算法应用于水库优化调度求解是可行和有效的。

水库优化调度;鲸鱼优化算法;智能优化算法;仿真验证

水库优化调度属多约束、非线性、多阶段组合优化问题。传统求解方法[1-5]随着水库数量或决策变量维数的增加,面临计算量大、“维数灾”等难题。智能优化算法由于具有概念简单、易于实现、无需梯度信息、避免局部最优解等特点在水库优化调度中得到广泛应用,如粒子群优化(particle swarm optimization,PSO)算法[6-8]、布谷鸟搜索(cuckoo search,CS)算法[9]、差分进化(differential evolution,DE)算法[10-11]、混合蛙跳算法(shuffled frog leaping algorithm,SFLA)[12-13]、狼群算法(wolf pack search,WPS)[14]、鸟群算法(bird swarm algorithm,BSA)[15]等,在水库优化调度中取得了一定的优化效果。然而,传统智能优化算法在实际应用中普遍存在早熟收敛、易陷入局部极值等不足，近年来,正弦余弦算法(sine cosine algorithm, SCA)[16]、风力驱动优化(wind driven optimization,WDO)算法[17]、足球联赛竞争(soccer league competition,SLC)算法[18]等新型仿生智能算法被陆续提出,并用于解决复杂优化问题,有效克服了传统智能算法的不足,已在函数优化及水资源评价等方面获得了较好的应用效果。鉴于此,本文将一种新型群智能仿生算法——鲸鱼优化算法(whale optimization algorithm,WOA)应用于水库优化调度问题中,旨在为水库优化调度问题的求解提供新的途径和方法。

1 水库优化调度模型

1.1 目标函数

以年发电量E最大为优化调度目标的数学模型可表示为[15]

(1)

式中:Ai为第i个电站出力系数;Qij为第i个电站第j时段的平均发电流量,m3/s;Hij为第i个电站第j时段的平均发电水头,m;R为水电站总数;T为总时段数(本文计算时段为月,T=12);Δt为时段长度,h。

1.2 约束条件

梯级水库之间存在复杂的水力联系和电力联系,考虑到水电站的经济运行要求,中长期调度时需要考虑水库水量平衡约束、水位约束、流量约束、出力约束和梯级水库间的水力联系约束[15]:

Vij+1=Vij+(qij-Qij-Sij)ΔT

(2)

Zij,min≤Zij≤Zij,max

(3)

Qij,min≤Qij+Sij≤Qij,max

(4)

Ni,min≤Ni≤Ni,max

(5)

qij=Qi-1,j+Si-1,j+Bij

(6)

式中:Vij+1、Vij分别为第i个电站第j时段初水库蓄水量;qij为第i个电站第j时段的平均入库流量;Sij为第i个电站第j时段的弃水流量;Qij为第i个电站第j时段的平均发电流量;Zij,min、Zij,max分别为第i个电站第j时段最低和最高限制水位;Zij为第i个电站第j时段的平均库水位;Qij,min、Qij,max分别为第i个电站第j时段最小与最大发电流量;Ni,min、Ni,max分别为第i个电站最小与最大限制出力;Bij为第i个电站第j时段的区间流入。

目前对该模型中的约束条件处理普遍采用搜索空间限定法和罚函数法两种方法[19],本文采用搜索空间限定法处理模型中的约束条件。

2 WOA及求解步骤

2.1WOA数学描述

鲸是世界上最大的哺乳动物,成年蓝鲸可达30 m长,质量180 t。研究表明,鲸在其大脑的特定区域有着类似于人类的梭形细胞，这些细胞负责情感、判断、社会等人类行为,换句话说,梭形细胞使鲸与其他生物不同。2016年, Mirjalili等[20]受座头鲸捕食行为的启发,提出一种基于自然灵感的新型启发式算法——WOA,该算法模仿座头鲸利用“螺旋气泡网”策略,并通过收缩包围、螺旋式位置更新及随机捕猎机制进行觅食,具有结构简单、调节参数少、收敛速度快及全局寻优能力强等特点。WOA数学模型包括环绕式捕食、发泡网攻击和搜索捕食3个阶段。

2.1.1 环绕式捕食

座头鲸能够识别猎物的位置并包围他们。假设当前的最佳鲸群个体位置(候选解)为目标猎物位置(目标猎物或接近最佳的目标猎物),其位置更新数学表达式为

Xj+1=Xj-A×D

(7)

式中:A和C为系数向量;X*为当前鲸群个体最佳空间位置;X为当前鲸群个体空间位置；j为当前迭代次数。

系数向量A和C计算方法如下:

A=2a×r-a

(8)

C=2r

(9)

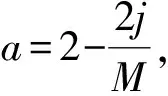
2.1.2 发泡网攻击

依据座头鲸气泡网觅食行为建立数学模型如下:

a. 收缩包围:该行为是通过减小式(8)中的a值来实现的;需要注意的是A的变动范围也随着a的减小而缩小。即设置的随机数A在[-1,1]之间,新鲸群个体搜索位置可以定义在当前鲸群个体位置和最佳鲸群个体位置之间的任意位置。

b. 螺旋式位置更新:该机制首先计算位于鲸群个体和猎物之间的距离,然后在鲸群个体和猎物的位置之间创建一个螺旋数学模型以模拟座头鲸的螺旋游动行为:

(10)

座头鲸在捕食收缩圆圈内沿着螺旋形路径来回游动,为了模拟这种同步行为,假设在更新鲸群个体位置过程中以50%的概率作为选择阈值,即要么选择收缩包围机制,要么选择螺旋式位置更新策略。数学模型为

(11)

式中p为[0,1]上的随机数。

2.1.3 搜索捕食

除了气泡网法搜索策略,座头鲸也随机搜索猎物。即基于向量A的变化方法同样可以用于搜索捕食。事实上,鲸群个体可依据彼此的位置随机搜索猎物。因此,在大于1或小于-1时A取随机值,并迫使鲸偏离猎物,借此搜索其他更合适的猎物,以增强算法的搜索捕食能力，使WOA能够进行全局搜索。数学模型为

X=Xrand-A×D

(12)

式中Xrand为从当前鲸群中随机选择的位置(随机鲸群个体)。

表1 典型测试函数

2.2 优化调度求解步骤

当今社会进入了网络时代，越来越多的企业员工上网学习、聊天、欣赏音乐，或者在公司的网页上通过论坛、QQ群、公共邮箱展开多渠道的交流沟通。应该看到，互联网在员工的精神生活中起着重要的作用。强化企业的精神激励机制，应该关注网络资源，增强员工精神生活的自控能力，有效抵御诸如诚信迷失、义利失衡、金钱崇拜、潜规则盛行等丑恶行径给人的思想侵蚀。要面对实际，端正利用网络资源的态度，使每一个员工获得取之不尽用之不竭的精神源泉。

用WOA求解水库优化调度的基本思想是:根据水库优化调度问题确定待优化参数,即决策变量,鲸群中每个个体所处空间位置均包含一组决策变量。通过适应度函数来衡量个体所处空间位置的优劣,利用鲸觅食策略不断更新鲸个体位置直至获取最佳鲸空间位置,即获得待优化问题的最佳决策变量。其求解步骤可归纳如下:

步骤1 划分水电站水库调度期时段,确定决策变量(本文以月末水位作为决策变量)及其取值范围。

步骤2 定义适应度函数。由于WOA是求解极小值,因此将式(1)的倒数作为适应度函数,即目标函数(约束条件同式(2)～(5)):

(13)

步骤3 WOA参数初始化。将各时段末水库水位Z1、Z2、…、ZRT看成R×T维决策空间鲸个体的位置X1、X2、…、XRT,在水位取值解空间范围内随机初始化鲸位置,并设置WOA参数,包括群体数目N、最大迭代次数M、对数螺旋形状常数b、当前迭代次数j及算法终止条件。

步骤4 利用式(13)适应度函数计算每个鲸群个体适应度值,找到并保存当前群体中最佳鲸群个体X*。

步骤5 若j≤M时,更新a、A、C、l和p。

步骤6 当p<0.5时,若A<1,利用式(7)更新当前鲸群个体的空间位置;若A≥1,则从当前群体中随机选择鲸群个体位置Xrand,并利用式(12)更新当前鲸群个体的空间位置。

步骤7 当p≥0.5时,利用式(10)更新当前鲸群个体的空间位置。

步骤8 利用式(13)适应度函数计算每个鲸群个体的适应度值,找到并保存当前群体中最佳鲸群个体X*。判断算法是否满足终止条件,若满足,则转到步骤9;否则,令j=j+1,重复执行步骤5～8。

步骤9 输出最优鲸群个体适应度值及所处空间位置X*,X*即为最佳决策变量月末水位。

3 仿真验证

利用4个典型测试函数(表1)对WOA的寻优能力进行仿真验证,并与CS、DE、SFLA、PSO、萤火虫算法(firefly algorithm,FA)和SCE-UA算法的仿真结果进行比较,见表2。表1中,Sphere为单峰函数,用于测试算法的收敛速度和寻优精度;Griewank、Rastrigin和Ackley为多峰函数,用于测试算法跳出局部极值及全局搜索的能力。实验参数设置如下:各算法最大迭代次数均取200;WOA群体数目为50,对数螺旋形状常数为2;CS算法鸟窝位置数为25,发现概率为0.25;DE算法种群规模为50,上下限的尺度因子分别为0.8、0.2,交叉率为0.2;SLFA青蛙群体规模为50,子群数为5,子群内青蛙个数为10,子群数局部进化次数为10;PSO算法种群规模为50,惯性因子为0.729,衰减系数为0.99,局部学习因子和全局学习因子均为2.0,个体速度限制为[-0.5,0.5];FA群体规模为30,最大吸引度为1，光强吸收系数为0.5、步长因子为0.2;SCE-UA复合形个数为50,每个复合形所包含的顶点数为5。

7种算法基于Matlab 2010a用M语言实现,对表1中4个测试函数重复进行20次寻优计算,并采用平均值、标准差2个参数进行评估,见表2。其中,寻优平均值反映的是算法在运行至最大迭代次数时可以达到的求解精度,标准差反映算法的收敛稳定性。

a. 从表2来看,对于单峰函数Sphere,WOA寻优精度高于CS、DE、SFLA、PSO、FA和SCE-UA算法26个数量级以上,表现出较好的寻优精度和收敛速度;对于多峰函数Griewank、Rastrigin和Ackley,WOA同样获得较好的寻优效果,其寻优精度优于CS、DE、SFLA、PSO、FA和SCE-UA算法8个数量级以上,具有较好的搜索平衡、极值寻优和跳出局部极值的能力。

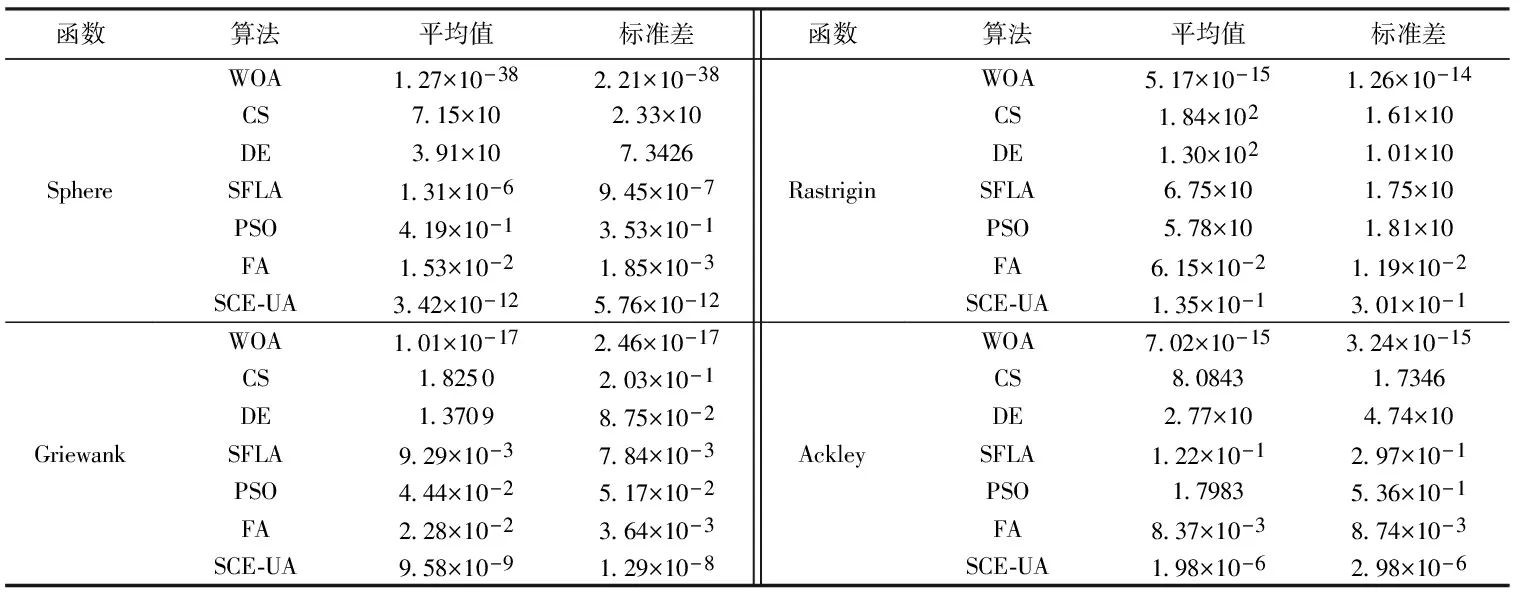
表2 函数优化对比结果

b. WOA对于4个测试函数的寻优标准差均在1.26×10-14以上,高于其他6种对比算法8个数量级以上,表现出较好的算法收敛稳定性。

c. 从表2仿真验证结果来看,各算法寻优效果从优至劣依次是:WOA、SCE-UA、FA、SFLA、PSO、DE、CS。

可见,在迭代200次条件下,无论是单峰还是多峰函数,WOA均获得了较好的寻优效果,算法具有调节参数少、收敛速度快、寻优精度高、全局寻优能力强以及收敛稳定性好等优点。

4 实例求解

4.1 单一水库优化调度

水库A以发电、防洪为主, 水库总库容8.96亿m3,有效库容4.45亿m3,正常蓄水位977 m,死水位952 m,保证出力185 MW,装机容量1 080 MW,出力系数8.0。已知该水库的水位-库容曲线、下游水位-下泻流量关系曲线,水库某水文年月预报来水以及该水库某年各时段水位的上下限，不考虑航运和灌溉任务,调度周期为1 a,计算各月月末水位,使整个调度期水库发电量最大。

依据上述优化求解步骤,以年发电量最大为准则,利用7种算法对调度模型进行求解,最终求解结果见表3,7种算法寻优过程线见图1(a)。

4.2 梯级水库优化调度

在水库A的基础上增加水库B进行梯级调度计算。水库B距离水库A 25.6 km,水库总库容1.96亿m3,调节库容0.71亿m3,正常蓄水位898 m,死水位888 m,装机容量420 MW,出力系数7.0(水库A出力系数8.5),两库区间来水忽略不计。同样已知该水库的水位-库容曲线、下游水位-下泻流量关系曲线,水库某水文年月预报来水以及该水库某年各时段水位上下限。调度周期为1 a,计算水库A和水库B各月月末水位,使该梯级水库调度期发电量最大。依据优化求解步骤,以年发电量最大为准则,利用7种算法对调度模型进行求解,最终求解结果见表4,7种算法寻优过程线见图1(b)。

表3 7种算法单一水库优化调度计算结果(20次平均)

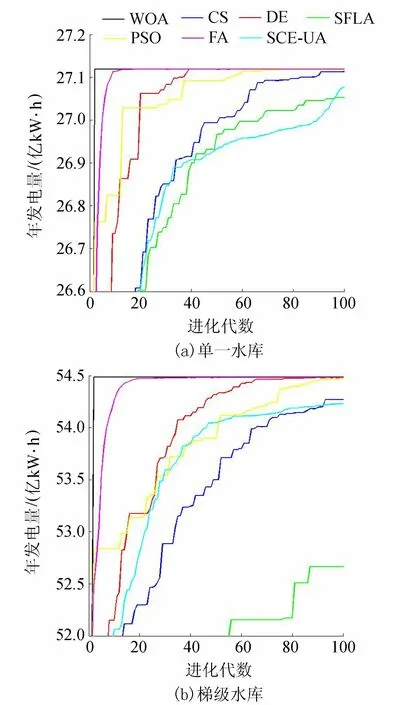
图1 7种算法模型求解进化过程

表4 7种算法梯级水库优化调度计算结果(20次平均)

4.3 调度结果及分析

a. 从表3及图1(a)可知,WOA、FA、DE算法的优化调度结果最大发电量均为27.118 3亿kW·h,优于其他4种算法优化调度结果。相比而言,WOA的平均计算时间(1.186 2 s)、收敛速度(10次迭代便逼近全局最优解)均优于其他6种算法。

b. 从表4及图1(b)来看,WOA的优化调度结果最大发电量为54.482 7亿kW·h,平均计算时间(2.882 4 s)、收敛速度(10次迭代便逼近全局最优解)均优于其他6种算法,再次验证了WOA具有较好的收敛速度、收敛精度和全局极值寻优能力。

c. 从实际工程验证结果来看,随着待优化问题的维数从单一水库的12维增至梯级水库的24维,求解难度随之增大,CS、DE、SFLA、PSO、FA和SCE-UA算法均无法获得全局最优解,而WOA由于有着良好的开发和勘探能力,获得了更好的寻优效果、平均计算时间和收敛速度。

5 结 论

a. 4个典型测试函数仿真结果表明,WOA有着良好的开发和勘探能力,其寻优效果远优于CA、DE、SFLA、CS、PSO和ABC等算法,具有收敛速度快、寻优精度高、全局极值寻优能力好等特点。

b. 工程实例优化调度验证结果表明,对于单一水库,WOA、FA、DE算法均具有较好的优化调度结果,但WOA的平均计算时间和收敛速度更佳;对于梯级水库,WOA的优化调度结果明显优于其他6种算法。

c. 通过典型测试函数及实际工程验证了WOA的可行性和高效性,可用于求解复杂、高维的梯级水库群优化调度模型。

[1] SHAWWASH Z K, SIU T K, RUSSELL S O D. The BC hydro short term hydro scheduling optimization model[J]. IEEE Transactions on Power Systems, 2000, 15(3): 1125-1131.

[2] GUAN X, LUH P B, ZHANG L. Nonlinear approximation method in Lagrangian relaxation-based algorithms for hydrothermal scheduling[J]. IEEE Transactions on Power Systems, 1995, 10(2): 772-778.

[3] 梅亚东.梯级水库优化调度的有后效性动态规划模型及应用[J].水科学进展,2000,11(2):195-198. (MEI Yadong.Dynamic programming model without markov in property of cascade reservoirs operation and its application[J].Advances in Water Science,2000,11(2):195-198. (in Chinese))

[4] 汪明,孙斌,林成,等.POA改进算法在乌江流域优化调度中的应用[J].水利水电科技进展,2010,30(增刊1):10-12. (WANG Qingming, SUN Bin, LIN Cheng,et al. POA improved algorithm in Wujiang optimal application[J]. Advances in Science and Technology of Water Resources,2010,30(Sup1):10-12. (in Chinese))

[5] 刘烨,钟平安,郭乐,等.基于多重迭代算法的梯级水库群调度图优化方法[J].水利水电科技进展,2015,35(1):85-88. (LIU Ye,ZHONG Pingan,GUO Le,et al. Operation chart optimization method of cascade reservoirs based on multiple iteration algorithm [J]. Advances in Science and Technology of Water Resources, 2015,35(1):85-88. (in Chinese))

[6] 杨道辉,马光文,过夏明,等.粒子群算法在水电站优化调度中的应用[J].水力发电学报,2006,25(5):5-7. (YANG Daohui,MA Guangwen,GUO Xiaming, et al. Particle swarm optimization in reservoir optimal operation using application[J].Journal of Hydroelectric Engineering, 2006,25(5):5-7. (in Chinese))

[7] 向波,纪昌明,罗庆松.免疫粒子群算法及其在水库优化调度中的应用[J].河海大学学报(自然科学版),2008,36(2):198-202. (XIANG Bo,JI Changming,LUO Qingsong. Immune particle swarm algorithm and its application in of reservoir optimization dispatch [J]. Journal of Hohai University(Natural Sciences), 2008,36(2):198-202. (in Chinese))

[8] 吴月秋,纪昌明,王丽萍,等.基于混沌粒子群算法的水电站水库优化调度[J].人民黄河,2008,30(11):96-98.(WU Yueqiu,JI Changming,WANG Liping, et al.Hydropower reservoir scheduling based on chaos particle swarm optimization[J].Yellow River, 2008,30(11):96-98. (in Chinese))[9] 明波,黄强,王义民,等.基于改进布谷鸟算法的梯级水库优化调度研究[J].水利学报,2015,46(3):341-349. (MING Bo,HUANG Qiang,WANG Yimin,et al.Cascade reservoir operation optimization based-on improved cuckoo search [J]. Journal of Hydraulic Engineering, 2015,46(3):341-349. (in Chinese))

[10] 郑慧涛,梅亚东,胡挺,等.改进差分进化算法在梯级水库优化调度中的应用[J].武汉大学学报(工学版),2013,46(1):57-61. (ZHENG Huitao,MEI Yadong,HU Ting,et al.Improved differential evolution algorithm in the cascade reservoirs application[J]. Engineering Journal of Wuhan University,2013,46(1):57-61. (in Chinese))

[11] 钟平安,张卫国,张玉兰,等.水电站发电优化调度的综合改进差分进化算法[J].水利学报,2014,45(10):1147-1155. (ZHONG Pingan,ZHANG Weiguo,ZHANG Yulan,et al.Comprehensive modified differential evolution algorithm for optimal operation of the hydropower station [J]. Journal of Hydraulic Engineering, 2014,45(10):1147-1155. (in Chinese))

[12] 纪昌明,李继伟,张新明.梯级水电站短期发电优化调度的免疫蛙跳算法应用研究[J].水力发电学报,2015,34(1):29-36.(JI Changming,Li Jiwei,ZHANG Xinming.Application of immune-shuffled frog-leaping algorithm to optimized operation of cascade hydropower stations for short-term power generation[J]. Journal of Hydroelectric Engineering, 2015, 34(1): 29-36. (in Chinese))

[13] 纪昌明,李继伟,张新明,等.基于免疫蛙跳算法的梯级水库群优化调度[J].系统工程理论实践, 2013, 33(8): 2125-2132. (JI Changming, LI Jiwei, ZHANG Xinming,et al.Optimal operation of cascade reservoirs based on immune-shuffled frog leaping algorithm[J].Systems Engineering-Theory & Practice,2013,33(8): 2125-2132. (in Chinese))

[14] 王建群,贾洋洋,肖庆元.狼群算法在水电站水库优化调度中的应用[J].水利水电科技进展,2015,35(3):1-4. (WANG Jianqun,JIA Yangyang,XIAO Qingyuan. Application of wolf pack search algorithm to optimal operation of hydropower station [J].Advances in Science and Technology of Water Resources,2015,35(3):1-4. (in Chinese))

[15] 崔东文,金波.改进鸟群算法及其在梯级水库优化调度中的应用[J].三峡大学学报(自然科学版),2016,38(6):4-14.(CUI Dongwen, JIN Bo.Improve bird swarm algorithm and its application in reservoir optimal operation[J].Journal of China Three Gorges University(Natural Sciences),2016,38(6):4-14. (in Chinese))

[16] 崔东文.正弦余弦算法-投影寻踪水污染物总量分配模型[J].水资源保护,2016,32(6):75-81.(CUI Dongwen.Sine cosine algorithm-projection pursuit model for water pollutant load allocation[J].Water Resources Protection,2016,32(6):75-81. (in Chinese))

[17] 崔东文,金波.基于WDO-PP模型的文山州近10年水资源承载力评价[J].水利经济,2016,34(6):43-49.(CUI Dongwen,JIN Bo. Evaluation of carrying capacity of water resources of Wenshan Prefecture in latest 10 years based on WDO-PP model [J].Journal of Economics of Water Resources,2016,34(6):43-49. (in Chinese))

[18] 崔东文.文山州近10年水资源利用效率评价SLC-PP模型及应用[J].河海大学学报(自然科学版),2017,45(2):129-136.(CUI Dongwen. Projection pursuit model for evaluation of water use efficiency based on soccer league competition algorithm[J]. Journal of Hohai University(Natural Sciences), 2017,45(2):129-136. (in Chinese))

[19] 吴学文.考虑生态的多目标水电站水库混沌优化调度研究[M].北京:中国水利水电出版社,2011.

[20] MIRJALILI S, LEWIS A. The whale optimization algorithm[J].Advances in Engineering Software, 2016，95：51-67.

Application of whale optimization algorithm in reservoir optimal operation//

CUI Dongwen

(WenshanWaterConservancyBureauofYunnanProvince,Wenshan663000,China)

In order to verify the feasibility and effectiveness of the whale optimization algorithm for reservoir optimal operation, four test functions were used in the whale optimization algorithm, and the simulated results were compared with those obtained from six algorithms, including the cuckoo search algorithm, differential evolution algorithm, shuffled frog leaping algorithm, particle swarm optimization algorithm, firefly algorithm, and SCE-UA algorithm. The whale optimization algorithm and the six comparison algorithms were used to solve the long-term optimal operation of a single reservoir and cascade reservoirs. The results show that the accuracy of the whale optimization algorithm is higher than that of the other six algorithms by eight or more orders of magnitude, and it has the fast convergence speed, high convergence precision, and excellent ability of optimization. The results of the whale optimization algorithm for the optimal operation of a single reservoir and cascade reservoirs are superior to those of the other six algorithms. The whale optimization algorithm is feasible and effective for reservoir optimal operation.

reservoir optimal operation; whale optimization algorithm; intelligent optimization algorithm; simulation verification

崔东文(1978—),男,教授级高级工程师,主要从事水资源管理与保护研究。E-mail:cdwgr@163.com

10.3880/j.issn.1006-7647.2017.03.012

TV697.1

A

1006-7647(2017)03-0072-05

2016-05-20 编辑：熊水斌)