Z比分数法在石油管材力学性能比对试验中的应用

梁明华，李东风，蔺卫平，李 娜，王 蕊

(中国石油集团石油管工程技术研究院，国家石油管材质量监督检验中心 陕西 西安 710077)

·试验研究·

Z比分数法在石油管材力学性能比对试验中的应用

梁明华，李东风，蔺卫平，李 娜，王 蕊

(中国石油集团石油管工程技术研究院，国家石油管材质量监督检验中心 陕西 西安 710077)

对Z比分数法进行了介绍，将该方法应用于国家石油管材质量监督检验中心组织进行的石油管材拉伸比对试验,利用该方法对测试数据进行了分析，对各实验室的测试结果作出判定；通过尤登图对测试数据进一步分析，结果表明离群数据所在实验室测试系统含有明显的系统误差。

Z比分数；比对试验；力学性能；尤登图

0 引 言

实验室间的比对试验可客观评价参与实验室数据的准确性和可靠性，也可从中找出问题并采取相关的补救措施，对实验室的质量控制和保证起到补充和完善的作用[1]。比对试验数据统计方法普遍采用的Z比分数法，该方法将参加实验室的检测结果转换为一个能力统计量，通过与能力标准比较来测评偏离指定值的程度[2]。CNAS-GL02《能力验证结果的统计处理和能力评价指南》[3]对该方法进行了描述。

本文对Z比分数法进行了介绍，并结合由国家石油管材质量监督检验中心组织进行的石油管材拉伸比对试验，用Z比分的方法对各实验室的测试结果作出判定，并通过尤登图对测试数据进行了分析，为相关机构和人员开展此项工作提供参考。

1 Z比分数法简介

1.1 Z比分数

Z比分数法是国际上普遍采用的能力统计量，Z比分数也叫标准分数。利用四分位数稳健统计方法处理结果时，Z比分数是一个数与平均数(中位值)的差再除以标准差( 标准IQR) 的过程。Z比分法是一种可以看出某分数在分布中相对位置的方法。Z比分数能够真实地反映1个分数距离平均数的相对标准距离。如果把每个分数都转换成Z比分数，那么每个Z比分数会以标准差为单位表示1个具体分数到平均数的距离或离差。

其公式如下：

式中，Z为稳健Z比分值；X为参与实验室的测定值；Q2为所有测得数据的中位值；IQR为各参加实验室所有测得数据的四分位距。

|Z|≤2 为满意值，说明检测机构的检测能力状况良好；2<|Z|<3为可疑值或有问题值，说明检测机构的检测能力状况存在一定问题；|Z|≥3为不满意值或离群值，说明检测机构检测能力状况不理想，存在较大问题。

1.2 标准IQR

参数IQR是四分位间距(interquartile range，IQR) ，又称四分位差，它是上四分位数与下四分位数的差。四分位数是将一组数据由小到大(或由大到小)排序后，用3个点将全部数据分为4等份，与这3个点位置上相对应的数值称为四分位数，分别记为Q1(第一四分位数，或低四分位数)、Q2(第二四分位数，即中位数)、Q3(第三四分位数，或高四分位数)。

四分位数的位置这样确定：Q1的位置 (N+1)/4；Q2的位置 2 (N+1) /4；Q3的位置 3(N+1)/4，式中N表示数据的个数，四分位数的位置可能是整数也可能是小数。

四分位距计算采用

IQR=Q3-Q1

( 1)

计算IQR的基本步骤如下。

将数据列从小到大排列X{ 1} ，X{ 2} ，…，X{N} 。若数据数目为奇数，则中位数Q2为X{ (N+ 1) /2}; 如果数据数目为偶数，则中位数为(X{N/2}+X{(N/2)+1}) /2。如果N是奇数，那么Q2是一个单一的中心值；如果N是偶数，那么Q2是两个中心值的平均。在大多数情况下Q1 和Q3 是通过数值之间的内插法获得的，其是与该小数位置相邻的两个整数位置上的标志值的加权平均数，权数的大小取决于两个整数位置距离的远近，距离越近，权数越大，距离越远，权数越小，权数之和等于1。

如：某系列数据为13、13.5、13.8、13.9、14、14.6、14.8、15、15.2、15.4，则三个四分位数的位置分别为：

Q1的位置 (N+1)/4 =(10+1)/4=2.75

Q2的位置(N+1) /2=(10+1)/2=5.5

Q3的位置3(N+1)/4=3(10+1)/4=8.25

则，Q1为第二项与第三项的加权平均，Q2为第五项与第六项的加权平均，Q3为第八项与第九项的加权平均。

Q1=0.25×第二项+0.75×第三项=0.25×13.5+0.75×13.8=13.73

Q2=0.5×第五项+0.5×第六项=0.5×14+0.5×14.6=14.3

Q3=0.75×第八项+0.25×第九项=0.75×15+0.25×15.2=15.05

IQR=Q3-Q1=1.32

四分位距与方差、标准差一样，表示统计资料中各变量的分散情形，四分位差反映了中间50%数据的离散程度，其数值越小，说明中间的数据越集中；其数值越大，说明中间的数据越分散，四分位间距更多为一种稳健统计。而标准IRQ=k×IRQ，k=0.741 3。四分位间距越大，说明数据分散程度越大，因此，采用标准IQR计算Z比分数更能说明问题。可以比对试验特定项目

数据的分散程度可以用健变异系数来衡量，用稳健CV表示。

稳健CV=标准化IQR/中位值 ×100%

2 应用

2.1 比对试验情况

此次比对试验由国家石油管材质量监督检验中心组织进行，共14家单位参与，包含石油天然气工业用输送管、管件、油井管及井下工具的制造和检验单位。比对试验用试样取自国内某厂生产的高钢级管线钢钢板。采用直径为12.5 mm的棒状拉伸试样，试样平行段长度65 mm，样品由国家石油管材质量监督检验中心统一制备，分发各实验室。要求参与实验室采用GB /T 228.1—2010《金属材料拉伸试验第1部分: 室温试验方法》进行试验[4]，测定项目包括抗拉强度Rm、屈服强度Rt0.5和断后伸长率A50mm。

2.2 比对试验检测数据统计

14个参与比对试验实验室检测数据见表1。为更加清晰直观表示每个实验室数据，将检测数据绘制成条形图，结果如图1～图3所示。从图中可以看出编号5和6两个实验室的强度数据偏差较大，其他数据均在统一范围内；编号为8的实验室断后伸长率数据偏小，其它实验室数据分布较集中，未见较大偏离者。

2.3 比对试验结果分析

根据表1，计算得出各实验室检测数据的Q1、Q2、Q3 值和计算标准IQR值，计算结果见表2。根据表2结果计算各试验室对应数据的Z比分数，得出比对试验结果，见表3。在全部14个试验室中，共有12个实验室的规定总延伸强度(Rt0.5)和抗拉强度(Rm)项目结果为满意，占所有参加本次比对实验室的85 .7 %, 结果为不满意的实验室有2个,占参加实验室总数的14.3 %；共有13个实验室的断后伸长率(A50mm)项目均为满意结果，占所有参加本次比对实验室的92.9 %, 结果为不满意的实验室有1个, 占参加实验室总数的7.1%。

从Z比分数结果得到的稳健变异系数可以衡量比对试验特定项目的分散程度。其中Rm指标为0.90%,Rt0.5为1.05%，A50mm为5.59 %，说明Rm与Rt0.5值具有较高的总体测量精密度, 而A50 mm指标的分散性较大。

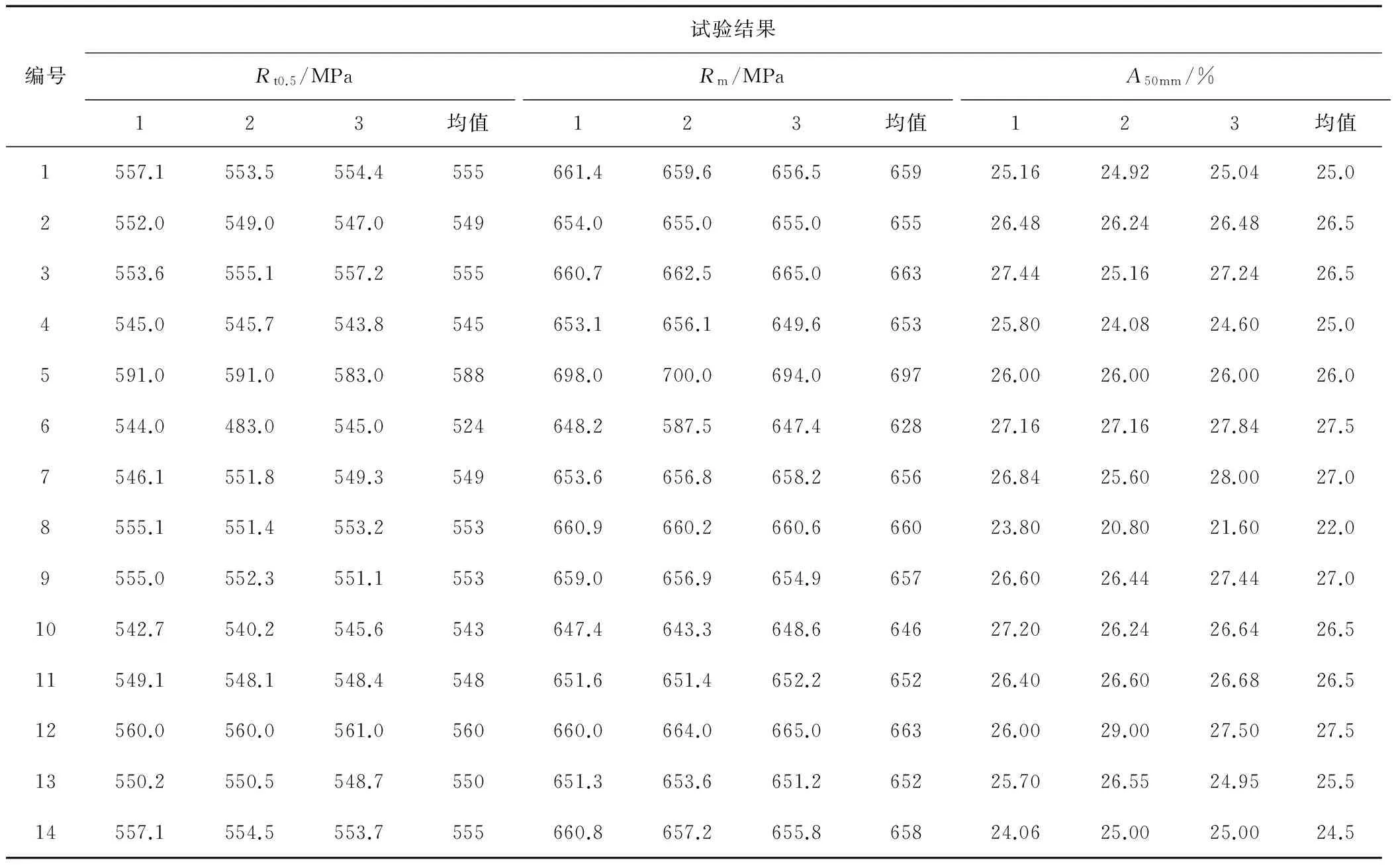
表1 比对试验检测结果统计表

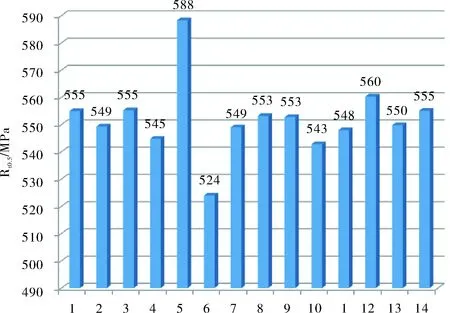
图1 屈服强度检测结果对比图

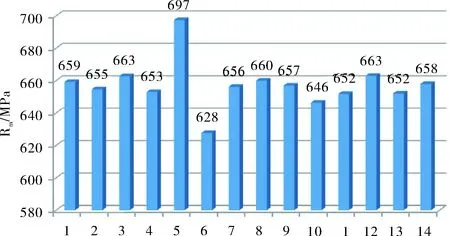
图2 抗拉强度检测结果对比图

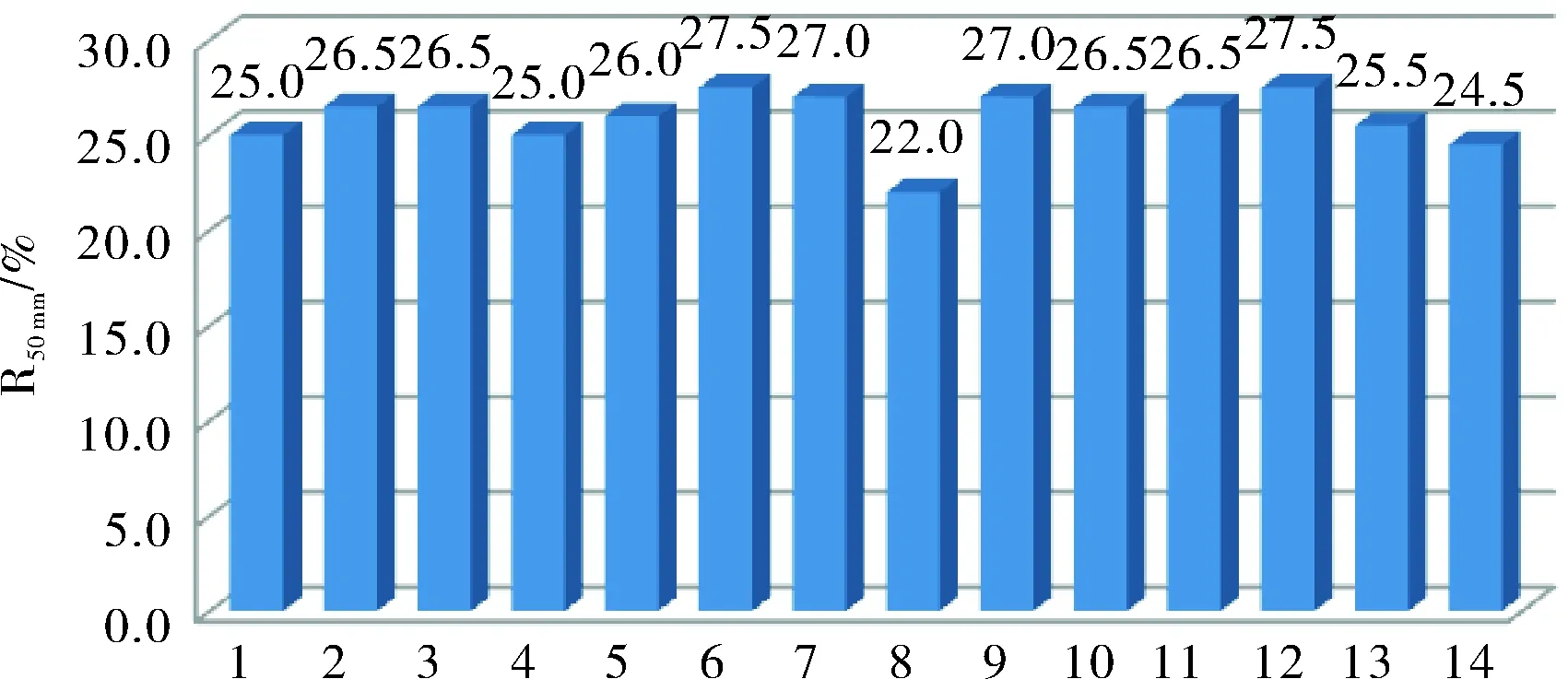
图3 断后伸长率检测结果对比图

3 影响因素分析

影响拉伸性能测定结果不确定度的因素很多，试验机载荷传感器的准确度级别、引伸计的准确度级别、试样尺寸, 包括试样原始横截面尺寸、试样原始标距和断后标距等都影响到测定结果的不确定度，其中断后标距测量时的位置选择受试验者主观因素与操作经验影响较大。此外，材料性能的均匀性、试样形状及其形状偏差、试验机拉伸速率、速度控制模式、试样夹持系统的夹具类型、试样垂直度、人为因素等均会对拉伸试验结果造成影响。

表2 检测结果Q1、Q2、Q3值及标准IQR计算结果

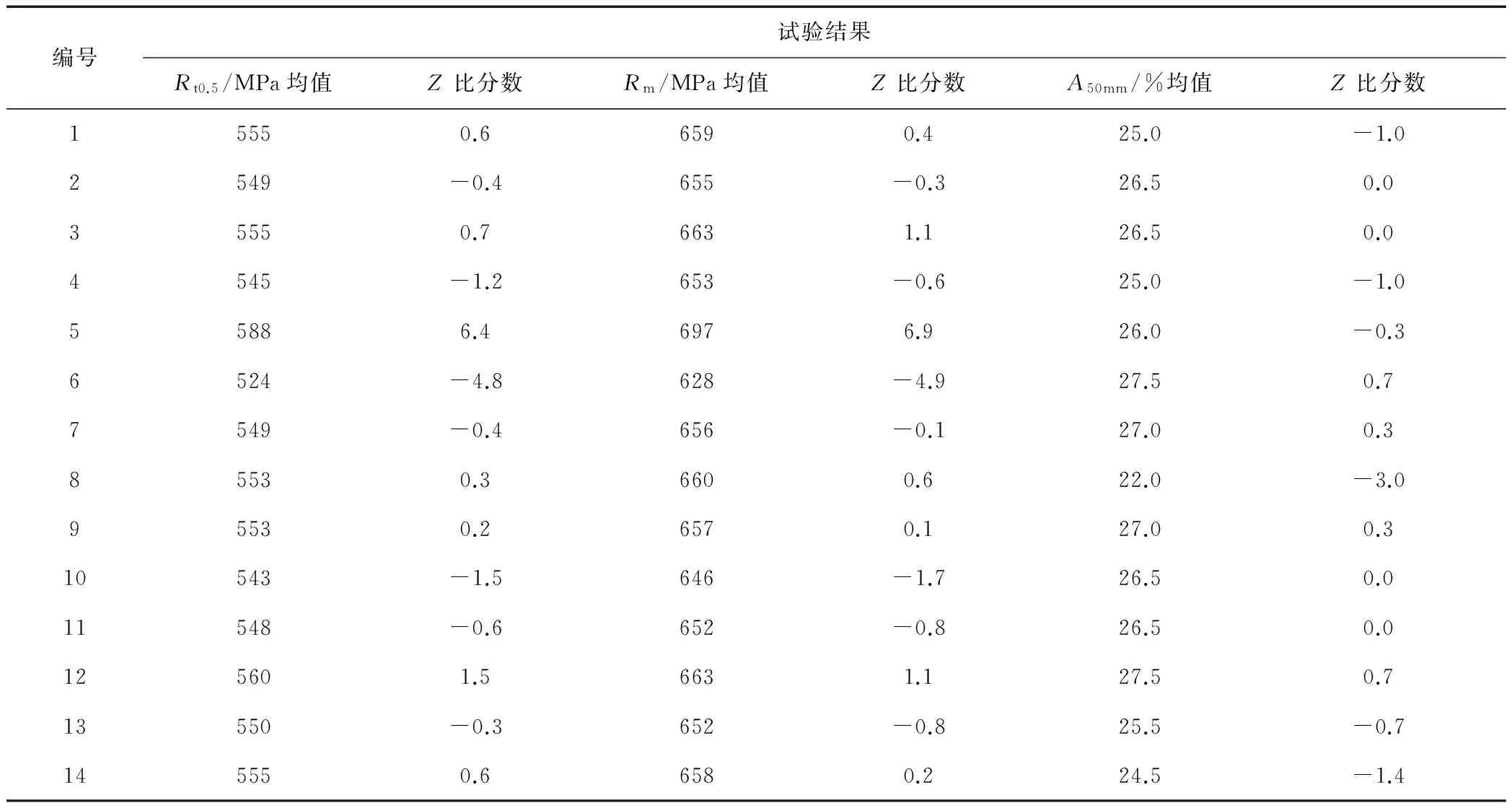
表3 比对试验结果

Youden图能直观、显著地表示出实验室的系统偏差。由于在同一台拉伸试验机上同时获得项目Rm与Rt0.5，因此以这两项结果做二维正态分布联合置信概率分析, 并同时引入稳健化处理, 消除离群数据对概率密度函数中心与长短轴的影响, 绘制Youden图，即可对试验机测力系统的能力水平给出直观的分析结果, 并反映力值传感器系统误差或随机误差对强度指标变异的影响[5]。尤登图中椭圆外的点，大体相当于那些Z比分数大于2 或小于-2 的值。尤登图的优点在于它们是真实数据的图示。在椭圆外的实验室能够看到它们的结果是怎样不同于其他的实验室。从尤登图可以说明：1) 含有明显系统误差的实验室(即实验室间变异)将在椭圆的右上象限或者在左下象限，即两个样品的结果异常地高或低；2) 随机误差(即实验室内变异)明显高于其他参加者的实验室将处于椭圆外的左上或右下象限，即一个样品的结果过高，而另一个则过低。

以每个实验室的结果Rt0.5为横坐标，Rm为纵坐标，就形成一系列数据点，用黑点·表示，如图4所示。图4中的椭圆表示约为95%概率的置信区域，椭圆边界已剔除了5号与6号实验室离群或可疑数据的干扰，椭圆的中心为二个样品中位值的交点。处于椭圆外的所有的点都标有相应的实验室编号。从图4中可以看出，厂家5和6分别分布于图的右上象限(第一象限)和左下象限(第三象限)。这就反映出实验室测试系统含有明显的系统误差(即实验室间变异), 因此拉伸试验机的传感器准确度、试样的初始尺寸测量以及拉伸试验的速度控制都应成为实验室技术核查与开展不确定度评定[ 6]时应注意的主要内容。

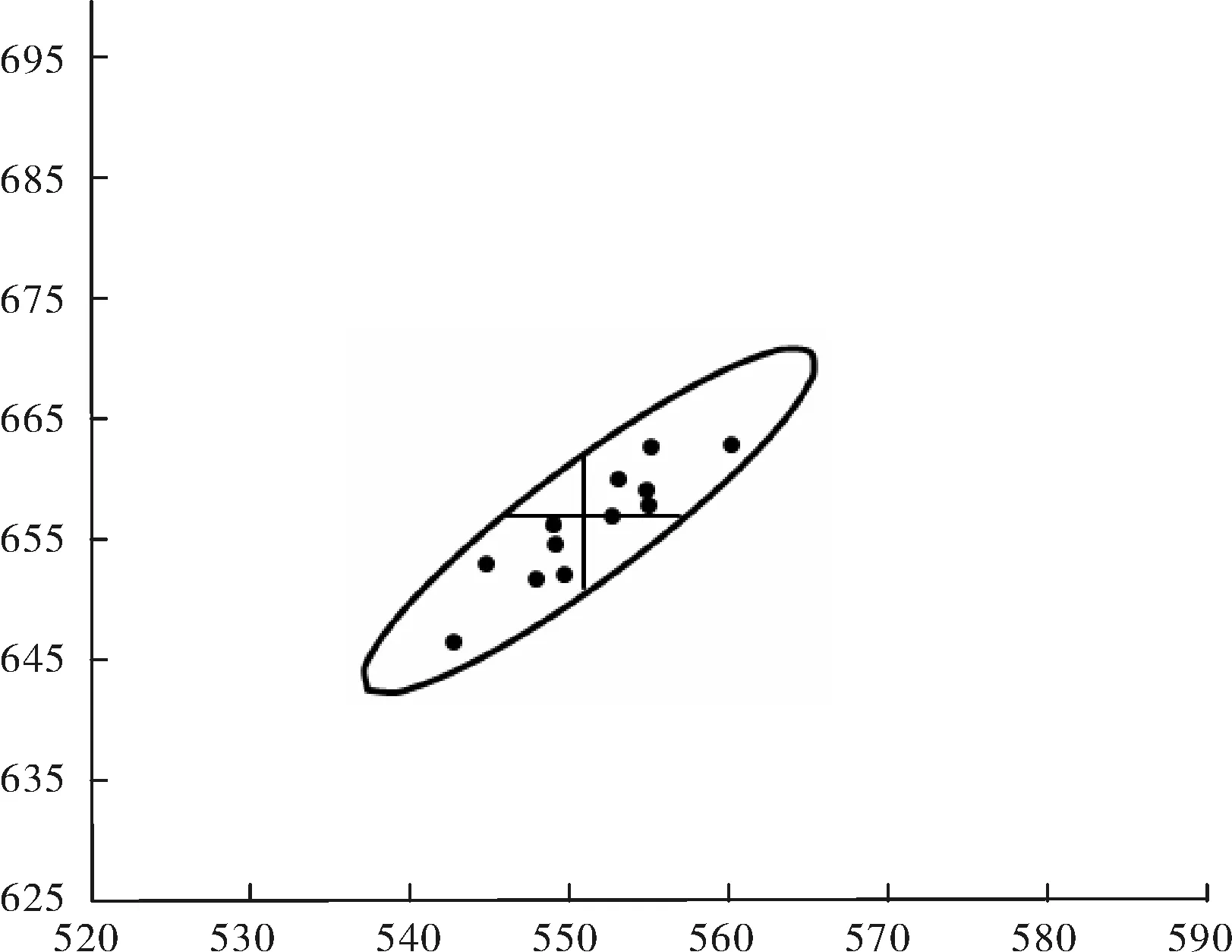
图4 强度指标二维联合置信概率分析尤登图

4 Z比分数法应用总结

1)介绍了Z比分数法，并利用该方法对参与国家石油管材质量监督检验中心组织进行的石油管材拉伸比对试结果进行了分析，对各实验室的测试结果做出判定。

2)通过对14家实验室结果数据实施稳健统计分析, 获得了表征验证试样强塑性能的公议结果(即中位值)。以总体分散性角度对比，Rm、Rt0.5与A50 mm依次增大。

3)通过强度指标二维联合置信概率尤登图对数据进行了分析，结果表明离群数据分布于尤登图的第一和第三象限，这就反映出实验室测试系统含有明显的系统误差。

[1] 中国合格评定国家认可委员会秘书处. 实验室认可与管理基础知识[M]. 北京:中国合格评定国家认可委员会，2007:94-112.

[2] 邢小茹，马小爽，田 文. 实验室间比对能力验证中的两种稳健统计技术探讨[J]. 中国环境监测,2011,27(4):4-8.

[3] 中国合格评定国家认可委员会. 能力验证结果的统计处理和能力评价指南:CNAS-GL02[S]. 北京: 中国标准出版社，2006．

[4] 中国国家标准化管理委员会．金属材料室温拉伸试验方法:GB/T 228.1-2010[S].北京: 中国标准出版社，2010．

[5] 方 健,魏毅静,范朝晖.拉伸试验的验证比对与延塑性指标能力分析[J] . 塑性工程学报,2007,14(2):1-6.

[6] 袁玉静, 钱绍圣.扩展不确定度分析与评定[J] .中国计量学院学报, 2004, 15(3):181-185.

Application of Z-score Method in the Tension Comparison Tests of Tubular Goods

LIANG Minghua, LI Dongfeng, LIN Weiping, LI Na, WANG Rui

(CNPCTubularGoodsResearchInstitute,NationalOilTubularGoodsQualitySupervisionandInspectionCenter,Xi′an,Shaanxi710077,China)

The Z-score method is introduced and used to analyze the data of tubular goods tension comparative tests which were organized by National Oil Tubular Goods Quality Supervision and Inspection Center. The test results of participating laboratories are judged by Z-score method. The Youden plot is used to further analyze the test data; The result shows that the test systems of outliers have obvious system error.

Z-score method； comparative tests； tensile property； Youden plot

梁明华，男，1979年生，高级工程师 ，2006年毕业于西安石油大学油气储运专业，获硕士学位，现主要从事石油管材的质量监督、检验与评价工作。E-mail：liangmh@cnpc.com.cn

TG115.5

A

2096-0077(2017)02-0023-05

10.19459/j.cnki.61-1500/te.2017.02.006

2016-09-06 编辑：葛明君)