Preparation of Macroscopic Entangled Coherent States in Nitrogen-Vacancy Centers Ensembles Coupled to a Superconducting Flux Qubit∗

Liang-Wei Wang(王亮伟)and Zhang-Cai Long(龙长才)

1State Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics,Wuhan Institute of Physics and Mathematics,Chinese Academy of Sciences,Wuhan 430071,China

2School of Physics,Huazhong University of Science and Technology,Wuhan 430074,China

1 Introduction

Entanglement severs as a basic resource for quantum information processing(QIP),and it plays a more and more significant role in the quantum mechanics.In recent years,many efforts have been devoted to the preparation of macroscopic quantum entanglement between the individual macroscopic systems[1−4]based on their unique quantum characteristics,[5−6]such as robustness to single-particle decoherence.Among various macroscopic quantum entangled states,the entangled coherent state(ECS)[7−12]has been paid particular attention in quantum computation science and QIP[13]due to their various applications in different aspects ranging from quantum communication,[14−16]quantum metrology,[17−18]and the quantum information theory.[19−20]Generation of these ESCs has attracted much interest in various kinds of systems,i.e.,micromechanical systems,[21]quantum dots,[22]cavity quantum electrodynamics(QED),[23]trapped ions,[24]and linear optical elements.[25−26]

On the other hand,as one of the most promising candidates for spin-based QIP,[27−32]the nitrogen-vacancy center(NVC)in diamond crystal,which is a point defect in the diamond,formed by the connecting of a nitrogen atom substituting for a carbon atom and an adjacent vacancy,and an additional electron usually trapped there.The NVC is of particular interest due to the following reasons:Firstly,the NVCs localized in the diamond need no extra cooling and trapping devices,which makes them more compatible with the superconducting circuit at room temperature than the atoms or ions.Secondly,the electron spins characterized by long coherence times in a millisecond level,and what is more,the nitrogen nuclear spins occupy longer life time in the scale of second,which are both helpful for reliable storage.[33]Thirdly,for the NVC,both the optical and microwave coherently manipulation are available,[33]which can be used as quantum interface for the state transfer of the photons in a microwave cavity to the ones trapped in an optical cavity.Finally,bene fiting from the collective magne-ticdipole coupling with the enhancement by a factorthrough the collective excitation of the nitrogen-vacancy center ensemble(NVE)in superconducting circuit QED or superconducting flux qubit(FQ),[34−39]whereNis the number of NVC in the spin ensemble.From both the theoretical and the experimental aspects,series of potential applications based on this collective-excitation mechanism have been investigated,i.e.,continuous variable quantum computation,[40]many-body system quantum simulation,[41]and high- fidelity quantum memory.[42−45]

Alternatively,through greatly simplifying the complicated trapping procedures,the quantum interface between superconducting gap-tunable FQ and NVE has also been obtained with the collective magnetic-coupling strength stronger by about three orders of magnitude than the coupling rate between the superconducting resonator and NVE.[46−56]As a result,much smaller number of NVCs in spin ensemble with longer coherence time is sufficient to achieve the desired coupling rate in this type of hybrid system,[53]which can potentially combine the best elements of each individual system:the long storage times available in NVEs for future large-scale quantum compu-tation,and the excellent tunability and scalability of the superconducting circuits QED.[49]

Therefore this hybrid quantum circuits consisting of a superconducting FB and NVE have attracted particular attention,and this physical model has the good potential to couple two or more separated spin ensembles in a scalable way.In this work we propose a hybrid device for generating arbitrary ECSs of two separate NVEs,using the collective magnetic coupling process,as well as the in situ tunability of the FQ.In the low-excitation limit,these collective excitations of the spin ensembles behave as the quantum harmonic oscillators,or the standard bosonic modes.We show that a macroscopic ECS of these two NVEs can be achieved with high-degree success possibilities,under the influence from the dissipation of the FQ and the dissipative/dephasing effects of NVEs.Furthermore,the ECS of spin ensembles with high-degree entanglement characterized by concurrence could also be generated through accurately controlling the FQ.Therefore,the present hybrid system not only becomes one of critical building blocks towards scalable solid-state quantum processor,but also provides another alternative path for accessing the many-body continuous variable quantum computation.

2 The System and Model

The system under consideration is shown in Fig.1,two ensembles of NVEs in diamond are glued,respectively,above and below the surface of superconducting gap-tunable FQ.Among the different types of superconducting qubits,the FQ has the advantage of high-level anharmonicity,and of strong coupling to the electromagnetic if elds.In our model,the superconducting gap-tunable FQ consists of a superconducting loop interrupted by four Josephson junctions(JJs)in which two junctions have the same JJ coupling energyEJ,and the other two JJs have the smaller JJ energiesζEJwith 0＜ζ＜1.The two spin ensembles are glued on the surface of the FQ and the distance between them is less than a micrometer.In the present model,the gap-tunable FQ could be treated as an effective two-level system with the Hamiltonian(in units of ħ =1)[49]Hf=[ε(Φext)σz+Δ()σx]/2 if we bias the main loop close to one-half of a flux quantum Φ0=h/2e.Throughout the paper,we denote the flux eigenstates|l〉and|r〉as the clockwise persistent current and counterclockwise persistent current,respectively.[57−59]Hereσz(σx)are the Pauli operators in the basis of flux eigenstates|l(r)〉.The energy splitting of the FQ can be characterized by ħε(Φext)=Ip(2Φext− Φ0)withIpthe FQ’s persistent current,and the flip of states of FQ could be controlled by the tunnel splitting energy ħΔ().Besides,the collective coupling between the FQ and spin ensembles could be obtained at the optimal point through independently adjusting these key parameters into the regime where the FQ has the longest coherence time.Note that the two internal magnetic fluxand Φextcan be tuned by the two additional microwave lines which are related to the key parameters Δ andεrespectively.It is essential to introduce an external magnetic fieldBwith two componentsBzandBx,where the former is parallel to the crystalline axis and the latter is perpendicular to the qubit loop.

Fig.1 (Color online)Schematic of the hybrid system,where two NVEs are attached on the surface of a fluxqubit.The inset shows the level structure of a single NVC,where we encode logical states|g〉and|e〉in the states|3A,ms=0〉,and|3A,ms= −1〉,respectively.

In the absence of external magnetic field,each NVC has a spin-triplet ground state and a zero- field splitting2.87 GHz betweenmS=0 and the sublevels|mS= ±1〉,which are nearly degenerate.[47,60]Furthermore,the FQ interacts with the spin ensembles through the magnetic fieldBfinduced by the persistent current in FQ,andBfcreates the superposition state of the|l〉and|r〉.Assumed that the strain-induced splitting is negligible,in contrast to the Zeeman splitting,[50]and the total Hamiltonian for the coupled system is

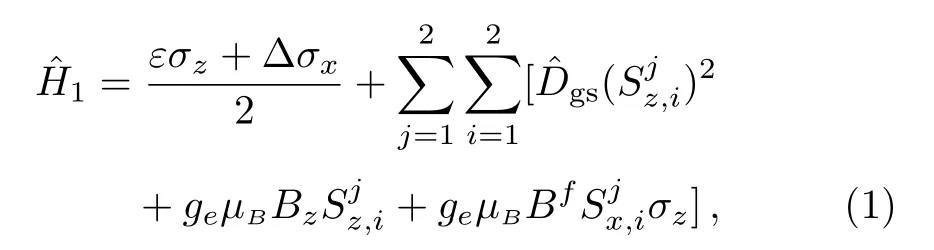
wherewithk=x,y,zare spin-1 Pauli operators with respect to thei-th NVC inside thej-th spin ensemble.µBis the Bohr magneton andgeis the ground-state Lander factor.The energy termgeµBBzrepresents the Zeeman splitting resulted from the part of the external magnetic field paralleled to thez-axis,namely,Bz.

To make the two-level approximation for each NVC well met,the crystalline axis of the NVCs are set to be parallel to the FQ’s surface,i.e.,thez-axis,and these degenerate sublevels|mS= ±1〉could be split by introducing an external magnetic field,which results in a two-level system denoted as|g〉=|3A,ms=0〉and|e〉=|3A,ms= −1〉,respectively.[46−47]In the subspace spanned by the|g〉and|e〉,we can change the Hamiltonianinto the following form

3 Preparation of ECS

In what follows,we describe how to obtain the ECS of NVEs in a deterministic way,through the following four key steps:

(i) Assuming that the system is initially prepared in the|ψ(0)〉=|0〉f|0〉1|0〉2,where|0〉fis the clockwise persistent-current state|l〉of the FQ,and|0〉j(j=1,2)is the ground state of the NVE,we apply a pulse nonadiabatically to modulate one of the control microwave lines to ensure that the values of Φextremains almost unchanged but that ofchanges dramatically,which keep the parametersεandGjalmost constant and satisfy the condition{Δ ≫ε}.As a result,this pulse drives the FQ into the degeneracy point with the evolution operatorU(t)=e−iΔσxt/2,and the states of the system|ψ(0)〉evolve into|ψ(t1)〉=(|0〉f− i|1〉f)|0〉1|0〉2without much disturbing the state of spin ensembles within the durationt1=π/2.Therefore,this first stepexpressed as|0〉f|0〉1|0〉2→ (|0〉f− i|1〉f)|0〉1|0〉2

We can find that the entanglement among the FQ and the two NVEs exists at this step.

(iv)To generate the ECS of NVEs,we need to measure the state of the FQ.This task can be performed by applying a pulse sequence to adc SQUID attached to the FQ(not shown in Fig.1),where the voltage state of the SQUID is very sensitive to the faint change of the flux,and depends on the switching probability of the energy eigenstates of the FQ.[47]So the two spin ensembles will be projected into the ECS|ψ−〉=|α〉1|β〉2− eitε|−α〉1|−β〉2or|ψ+〉=|α〉1|β〉2+eitε|−α〉1|−β〉2,corresponding to the readout from the state|0〉for|1〉fwith respect to the FQ,respectively.This implies that each ECS could be obtained with the success possibility of 50%.

All the above steps can be summarized as

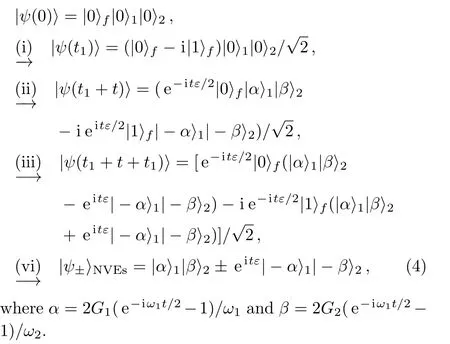
Next we will study the influence from dissipative effect of the FQ and the dissipative/dephasing effect of NVEs.Note that the evolution time of the steps(i)and(iii)is much shorter than that of the step(ii)due to Δ ≫ {ϵ,Gj}.So below we may focus the dissipation/dephasing effect only during the step(ii)using the master equation

where Γ andκare the decay rate and dephasing rate of the NVE,andγis the decay rate of FQ.For simplicity,we have assumed that Γ1= Γ2= Γ,κ1=κ2=κ.The differential equations about the density matrix of the FQ could be obtained by using the superoperator technique[63]and Hausdorffsimilarity transformation[64]with the form

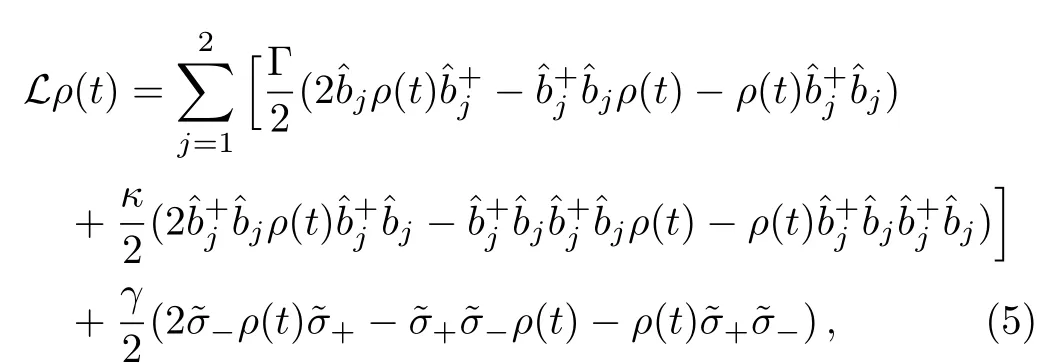
Then we can solve the above differentialwith the initial state|ψ(t1)〉=(|+〉f+|−〉f)|0〉1|0〉2/and obtain the time-dependent density matrix

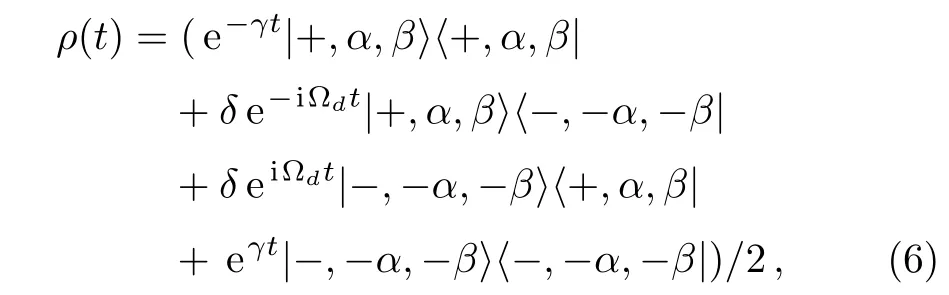
whereδ=exp[−γt/2−3)/Γ2−κt]is a factor with respect to the competition between the dissipation/dephasing effect and the spin-boson coupling process.

After the step(iii),the final state of the NVEs,with the readout of the FQ being|0〉f,turns to be

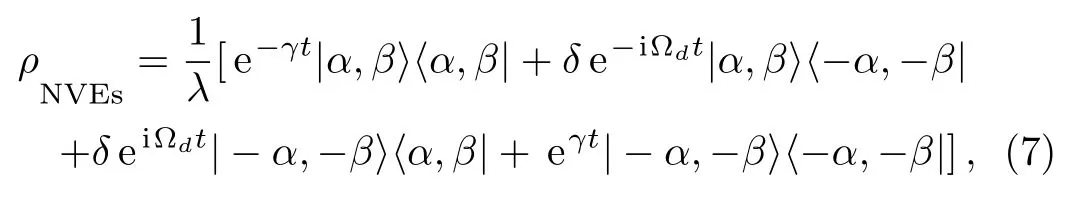
where the normalization constant is

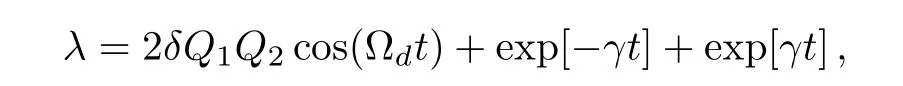
whereQ1= 〈α|−α〉andQ2= 〈β|−β〉.Similarly,we can obtain the other results if the measurement of state of the FQ is|1〉f.

Before using the concept of concurrence for bipartite entangled nonorthogonal states[65]to measure entanglement between the NVEs,we make a suitable transformation on Eq.(7)from the nonorthogonal form of Eq.(7)into an orthogonal form by rebuilding two orthogonal and normalized states as basis of the twodimensional Hilbert space,i.e.,we define|0〉1=|α〉1,

Therefore the concurrence for the ECS of spin ensembles has the following form

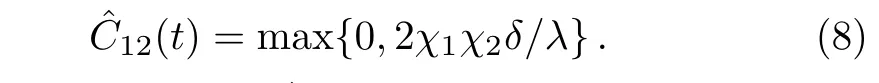
The time-dependentˆC12(t)is plotted in Fig.2,which shows the decoherence effect on the evolution of entanglement between spin ensembles.It is clear that,the concurrence of two NVEs increases firstly and then decreases gradually to disappear,which could be explained by the presence of the factorδin the expression ofˆC12(t).One can find that the entanglement is destroyed because the parameterδbecomes smaller and smaller when time passes.So to carry out our scheme more efficiently,we have to suppress these imperfect factors as much as we can.

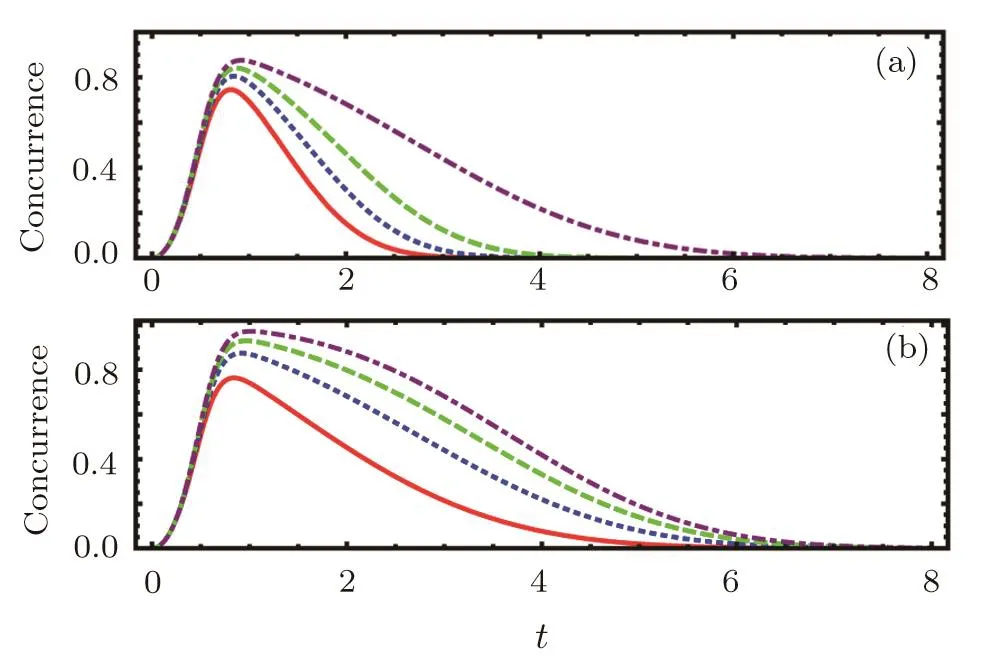
Fig.2 (Color online)The time evolution of the concurrence of the ECS,where the time parameter is dimensionless and we set ε=2.5,and G1=G2=1.(a)The four curves from bottom to top correspond to the case of Γ=0.2,0.1,0.05,and 0.01,respectively,where γ=0.1.(b)The four curves from bottom to top correspond to the case of γ=0.2,0.1,0.05,and 0.01,respectively,where Γ=0.01,and κ=0.01.

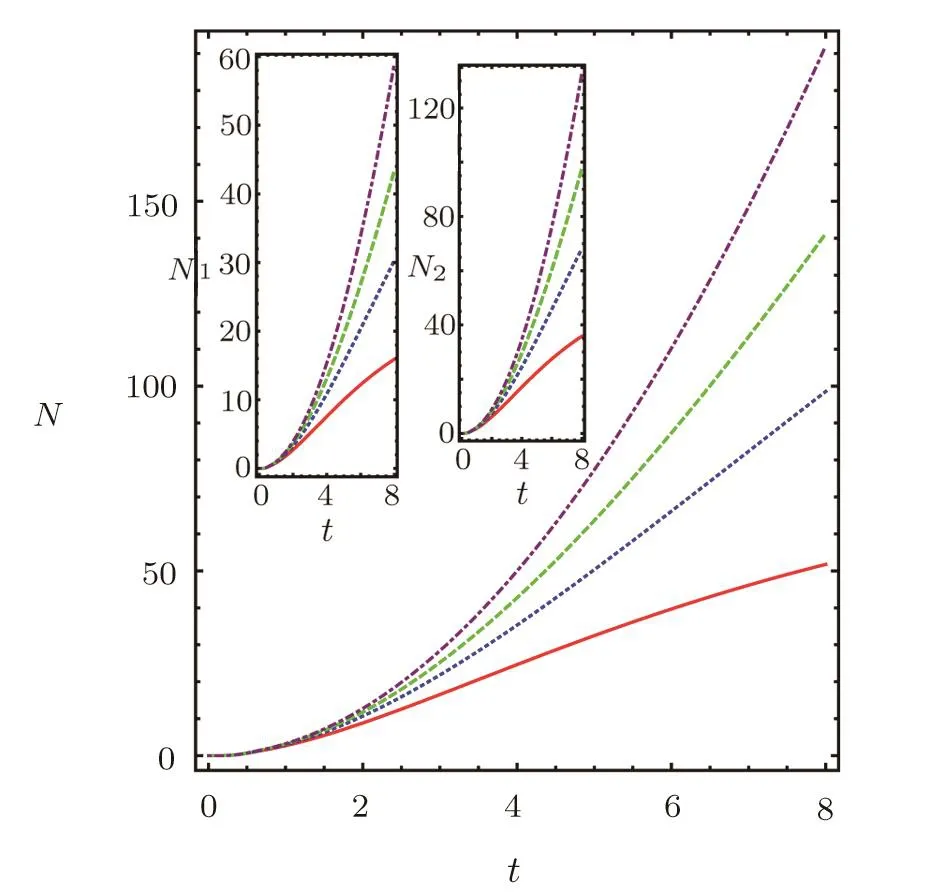
Fig.3 (Color online)The time evolution of the total photon number N in two NVEs,and the inset shows the photon number N1and N2.The four curves from bottom to top correspond to the case of Γ=0.2,0.1,0.05,and 0.01,respectively.The time parameter is dimensionless and we set γ =0.1,κ =0.01,ε =2.5,G1=1,and G2=1.5.

The HP transformation used on the NVEs requires that the total number of excitations in two NVEs are much smaller than the number of NVCs in each spin ensemble. Through calculation on Eq.(8),the average photon number in the two NVEs has the following relationN1=2|α|2ξ/λ,andN2=2|β|2ξ/λwithξ= −2δQ1Q2cos(εt)+exp[−2γt]+exp[2γt].In order to get some insight,we show the time evolution of the average photon numberN1(N2)andN=N1+N2in the present system.As shown in Fig.3,the value ofNis smaller than 200.So the small value of excitation number ensures that the HP transformation in our scheme is reasonable.

4 Discussion and Conclusion

We now survey the relevant experimental parameters.First,to ensure that the collective magnetic coupling could obtain the maximal values,the spin ensembles should be located symmetrically in the position where the magnetic field of resonator is maximal.Second,the feasibility of our scheme could be confirmed by series of experimental demonstration of in excellent quantum control in the quantum hybrid system consisting of a superconducting FQ and NVE,with the strong magnetic coupling strength–dozens of MHz.Based on a recent experimental work,[47]the coupling rate can be close to 70 MHz.Therefore,the operation time for obtaining the ECS of NVEs with high values of concurrence is about 0.2µs in our proposal,if the parameters are set asG1=G2=50 MHz,which is much shorter than the coherence times of NVCs and FQ.Finally,the electronic relaxation time of NVCs could reachT1−6 ms in the case of room-temperature,[66]even reach about two hundred seconds if the NVC is operated at lower temperature.[67]Additionally,the dephasing time of NVC can be greatly enhanced by decoupling the electron spin from its local environment using the method of spin echo.Based this technique,the dephasing timeT2for NVE reaches 3.7µs even at room-temperature,[19]and the dephasing timeT2for NVE with natural abundance of13C has been reported that it could reach 0.6 ms,[68]which has been prolonged to beT2=1.8 ms for the isotopically pure diamond sample.[69]

We emphasize that the present method provides us the potential feasibility of generating multi-NVE entanglement,which is a crucial element in the NVE-based scalable quantum network.We emphasize that the multi-NVE dynamics itself is more complicated and could show richer dynamical behavior than the previous two-qubit case.[70−72]Therefore,it is desirable to investigate the quantum dynamics of spin ensembles in a scalable way,and to develop efficient methods for tuning the entanglement among many NVEs in a common resonator.However,this issue goes beyond the scope of the present paper.Noticeably,the multi-NVE dynamics in different model have been studied for large-scale arrays.[73]

Note that the preparation of ECS of spin ensembles depends on the state of FQ,therefore we can realize this goal by probing microwave transmission through a resonator coupled to this FQ in the dispersive regime of circuit QED,or by using the bifurcation phenomenon of a non-linear resonator with the Josephson bifurcation amplifier,[74]where the expectation value of the observable to be measured is preserved during the measurement.In general,the above mentioned quantum measurement methods project the qubit states into an eigenstate of the measured observable in a discrete(stochastic)way when the unitary evolution is continuous(deterministic).Therefore,it is necessary to utilize quantum non-demolition measurements,[75−77]where,the interaction Hamiltonian between the system and the measurement apparatus commutes with the system Hamiltonian,and this novel feature guarantees both minimum disturbance to the relevant system and an accurate measurement result.In our case,we can distinguish the qubit state through detecting the small magnetic field from the supercurrent.

Next we check the operation time for the step(i)–(iv)for the preparation of ECS.Note that the evolution time of the steps(ii)is much longer than that of the other steps,we obtain the operation time is aboutt1=π/2Δ,which is about 0.02µs in the case of Δ =500 MHz,and is much shorter the decoherence time of NVE.Another problem is the detection of the ECS,and it can be realized by transferring the state from the NVEs to the states of two additional smaller flux qubits.Therfore the direct measurement on the states of flux qubits could complete the entanglement dectection.We emphasize that the coupling strength between the larger qubit and each NV center should be proportional to that between the smaller qubit and NV centers.

In conclusion,we have proposed a potentially practical scheme for creating arbitrary macroscopic ECSs between two separate spin ensembles through the collective magnetic coupling to the FQ.We have shown that the ECS of NVEs can be achieved with high success possibilities even under the influence from the decoherence of FQ and NVEs.More importantly,our idea is close to being reachable with currently available technology.Since the macroscopic ECSs are of crucial importance for continuousvariable quantum computation and quantum communication,we argue our work to be potentially practical for realizing large-scale one-way quantum computation[78−79]in solid-state quantum system.

References

[1]L.M.Duan,Phys.Rev.Lett.88(2002)170402.

[2]L.Li,Y.O.Dudin,and A.Kuzmich,Nature(London)498(2013)466.

[3]B.Julsgaard,A.Kozhekin,and E.S.Polzik,Nature(London)413(2001)400.

[4]A.Sorensen,L.M.Duan,J.I.Cirac,and P.Zoller,Nature(London)409(2001)63.

[5]M.D.Lukin,S.F.Yelin,and M.Fleischhauer,Phys.Rev.Lett.84(2000)4232.

[6]S.L.Braunstein and H.J.Kimble,Phys.Rev.Lett.80(1998)869.

[7]B.C.Sanders,Phys.Rev.A 45(1992)6811.

[8]W.M.Zhang,D.H.Feng,and R.Gilmore,Rev.Mod.Phys.62(1990)867.

[9]M.Y.Chen,M.W.Y.Tu,and W.M.Zhang,Phys.Rev.B 80(2009)214538.

[10]W.L.Song,Z.Q.Yin,W.L.Yang,X.B.Zhu,F.Zhou,and M.Feng,Sci.Rep.5(2015)7755.

[11]L.Zhou and H.Xiong,J.Phys.B 41(2008)025501.

[12]Q.Chen,W.L.Yang,and M.Feng,Phys.Rev.A 86(2012)045801.

[13]M.A.Nielsen,and I.L.Chuang,Quantum Computation and Quantum Information,Cambridge University Press,Cambridge,UK(2000).

[14]V.J.S.Enk and O.Hirota,Phys.Rev.A 64(2001)022313.

[15]K.Park and H.Jeong,Phys.Rev.A 82(2010)062325.

[16]K.Azuma and G.Kato,Phys.Rev.A 85(2012)060303(R).

[17]J.Joo,W.J.Munro,and T.P.Spiller,Phys.Rev.Lett.107(2011)083601.

[18]J.Joo,K.Park,H.Jeong,W.J.Munro,K.Nemoto,and T.P.Spiller,Phys.Rev.A 86(2012)043828.

[19]H.Jeong,M.Paternostro,and T.C.Ralph,Phys.Rev.Lett.102(2009)060403.

[20]M.Paternostro and H.Jeong,Phys.Rev.A 81(2010)032115.

[21]A.D.Armour,M.P.Blencowe,and K.C.Schwab,Phys.Rev.Lett.88(2002)148301.

[22]X.G.Wang,M.Feng,and B.C.Sanders,Phys.Rev.A 67(2003)022302.

[23]E.Solano,G.S.Agarwal,and H.Walther,Phys.Rev.Lett.90(2003)027903.

[24]W.J.Munro,G.J.Milburn,and B.C.Sanders,Phys.Rev.A 62(2000)052108.

[25]N.B.An,Phys.Rev.A 69(2004)022315.

[26]N.B.An and J.Kim,Phys.Rev.A 80(2009)042316.

[27]L.Jiang,et al.,Science 326(2009)267.

[28]P.Neumman,et al.,Nat.Phys.6(2010)249.

[29]E.Togan,et al.,Nature(London)466(2010)730.

[30]W.L.Yang,J.H.An,C.Zhang,M.Feng,and C.H.Oh,Phys.Rev.A 87(2013)022312.

[31]J.B.You,W.L.Yang,Z.Y.Xu,A.H.Chan,and C.H.Oh,Phys.Rev.B 90(2014)195112.

[32]Q.Z.Hou,W.L.Yang,Z.Q.Yin,and C.Y.Chen,Sci.Rep.6(2016)37542.

[33]A.M.Stoneham,Physics 2(2009)34.

[34]Y.Kubo,et al.,Phys.Rev.Lett.105(2010)140502.

[35]D.I.Schuster,et al.,Phys.Rev.Lett.105(2010)140501.

[36]R.Amsüss,et al.,Phys.Rev.Lett.107(2011)060502.

[37]V.Ranjan,et al.,Phys.Rev.Lett.110(2013)067004.

[38]C.Grezes,et al.,Phys.Rev.X 4(2014)021049.

[39]H.Huebl,et al.,Phys.Rev.Lett.111(2013)127003.

[40]W.L.Yang,Z.Q.Yin,Q.Chen,C.Y.Chen,and M.Feng,Phys.Rev.A 85(2012)022324.

[41]W.L.Yang,et al.,Phys.Rev.A 86(2012)012307.

[42]Y.Kubo,C.Grezes,A.Dewes,and T.Umeda,Phys.Rev.Lett.107(2011)220501.

[43]W.L.Yang,Z.Q.Yin,Y.Hu,M.Feng,and J.F.Du,Phys.Rev.A 84(2011)010301(R).

[44]Y.Kubo,et al.,Phys.Rev.A 85(2012)012333.

[45]B.Julsgaard,C.Grezes,P.Bertet,and K.Mølmer,Phys.Rev.Lett.110(2013)250503.

[46]D.Marcos,M.Wubs,J.M.Taylor,R.Aguado,M.D.Lukin,and A.S.Søensen,Phys.Rev.Lett.105(2010)210501.

[47]X.Zhu,et al.,Nature(London)478(2011)221.

[48]X.Zhu,et al.,Nat.Commun.5(2014)3424.

[49]S.Saito,et al.,Phys.Rev.Lett.111(2013)107008.

[50]Z.L.Xiang,S.Ashhab,J.Q.You,and F.Nori,Rev.Mod.Phys.85(2013)623.

[51]Z.L.Xiang,X.Y.Lü,T.F.Li,J.Q.You and F.Nori,Phys.Rev.B 87(2013)144516.

[52]X.Y.Lü,Z.E.Xiang,W.Cui,J.Q.You,and F.Nori,Phys.Rev.A 88(2013)012329.

[53]Q.Chen,W.L.Yang,and M.Feng,Phys.Rev.A 86(2012)022327.

[54]S.L.Ma,P.B.Li,A.P.Fang,S.Y.Gao,and F.L.Li,Phys.Rev.A 88(2013)013837.

[55]J.Cai,F.Jelezko,N.Katz,A.Retzker,and M.B.Plenio,New.J.Phys.14(2012)093030.

[56]T.Hümmer,G.M.Reuther,P.Hänggi,and D.Zueco,Phys.Rev.A 85(2012)052320.

[57]X.Zhu,A.Kemp,S.Saito,and K.Semba,Appl.Phys.Lett.97(2010)102503.

[58]F.G.Paauw,A.Fedorov,C.J.P.M.Harmans,and J.E.Mooij,Phys.Rev.Lett.102(2009)090501.

[59]A.Fedorov,et al.,Phys.Rev.Lett.105(2010)060503.

[60]N.B.Manson,J.P.Harrison,and M.J.Sellars,Phys.Rev.B 74(2006)104303.

[61]K.Hammerer,A.S.Sørensen,and E.S.Polzik,Rev.Mod.Phys.82(2010)1041.

[62]G.Chen,H.Zhang,Y.G.Yang,R.Wang,L.Xiao,and S.Jia,Phys.Rev.A 82(2010)013601.

[63]J.G.P.de Faria and M.C.Nemes,Phys.Rev.A 59(1999)3918.

[64]W.Witschel,Int.J.Quant.Chem.20(1981)1233.

[65]X.G.Wang,J.Phys.A 35(2002)165.

[66]P.Neumann,et al.,Science 320(2008)1326.

[67]J.Harrison,M.J.Sellars,and N.B.Manson,Diam.Relat.Mater.15(2006)586.

[68]P.L.Stanwix,et al.,Phys.Rev.B 82(2010)201201.

[69]G.Balasubramanian,et al.,Nat.Materials 8(2009)383.

[70]J.I.de Vicente,T.Carle,C.Streitberger,and B.Kraus,Phys.Rev.Lett.108(2012)060501.

[71]S.Armstrong,et al.,Nat.Phys.11(2015)167.

[72]W.L.Song,W.L.Yang,Q.Chen,Q.Z.Hou,and M.Feng,Opt.Express 23(2015)13734.

[73]F.Badshah,S.Qamar,and M.Paternostro,Phys.Rev.A 90(2014)033813.

[74]K.Kakuyanagi,T.Baba,Y.Matsuzaki,H.Nakano,S.Saito,and K.Semba,New.J.Phys.17(2015)063035.

[75]P.Grangier,J.A.Levenson,and J.P.Poizat,Nature(London)396(1998)537.

[76]A.Lupa¸scu,et al.,Nat.Phys.3(2007)119.

[77]T.Picot,A.Lupa¸scu,S.Saito,C.J.P.M.Harmans,and J.E.Mooij,Phys.Rev.B 78(2008)132508.

[78]H.J.Briegel and R.Raussendorf,Phys.Rev.Lett.86(2001)910.

[79]R.Raussendorf and H.J.Briegel,Phys.Rev.Lett.86(2001)5188.