畸形波作用下双层水平板防波堤压力分布特性研究

顾倩，张宁川*

(1.大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024)

畸形波作用下双层水平板防波堤压力分布特性研究

顾倩1，张宁川1*

(1.大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024)

基于物理模型试验，考虑畸形波参数、相对板宽、相对波高等影响因素，就畸形波对平顶双层水平板防波堤作用进行研究。首先对畸形波作用下双层水平板的波浪力分布特征进行了讨论，然后就最大波动压强、结构最大总垂向力与不规则波作用进行了对比分析。结果表明，畸形波作用下，双层水平板最大波动压力出现在前端迎浪区域附近，向尾端逐渐递减。双层水平板4个受力面的压力分布不同且有相位差，4个受力面的最大波动压力时间差约在0.1Tp～0.4Tp范围内变化。与不规则波作用比较，畸形波作用没有显著改变波压包络分布特征，但增大了波压包络强度值。试验范围内，就最大总力而言，两者最大总浮托力比值在1.06～2.45间变化；向下的最大总垂向力比值在1.22～2.07之间变化；就波动压力而言，其增大的幅度与畸形波参数α1相关性最强，随α1的增大而增大，在α1=2.04～3.1试验范围内，畸形波作用时的最大压强比不规则波作用时可约增大20%～80%。就最大波吸力而言，两者的比值与畸形波参数α4相关性最强，随α4的增大而减小。在α4=0.62～0.75试验范围内，最大波吸力强度的比值在1.61～0.87范围内变化。当α4≤0.72时，畸形波作用时的最大波吸力大于不规则波作用时的最大波吸力；当α4>0.72时则刚好相反。

畸形波；双层水平板式防波堤；波浪荷载；物理模型试验

1 引言

目前已经公认畸形波广泛存在于包括近岸水域在内的海洋中的各个区域，如Sand等[1]、Chien和Kao[2]、Melville[3]、Mori等[4]分别报道的丹麦大陆架海域、中国台湾海域、墨西哥湾附近海域及日本海附近海域的畸形波。Nikolkina和Didenkulova[5]对发生在世界各地发生的畸形波进行了综合分析认为，畸形波发生具有广泛性和非低概率性，特别指出近岸海域发生畸形波的概率可能大于、至少不小于外海。

鉴于畸形波发生区域的广泛性和发生概率可能超过诸多港口、海洋结构物设计波浪标准的重现期(对应的概率)，同时畸形波对海上结构的破坏作用巨大(如北海的“新年波”[6]彻底摧毁了Draupner石油平台)，开展畸形波对近岸结构物作用研究的意义就显而易见。双层水平板结构被认为是对深水适应能力更强、投资量随水深增加不敏感、同时具有防浪、透流双重功能的一种待开发的、有可预见应用潜力的一种新型防波堤结构。开展畸形波对双层水平板防波堤作用的研究，具有推广应用该结构的现实意义，同时也具有开展畸形波对近岸结构作用研究的示范意义。

国内外学者对于常规波浪作用下双层水平板已有大量的研究[7—14]，综合研究结果表明，双层水平板型防波堤的消浪效果至少不低于同等堤宽的浮体防波堤，其主要波浪荷载为垂向荷载。相关研究者还总结了双层水平板型防波堤的消浪系数及波浪垂向荷载计算的经验方法。

畸形波对于板式防波堤的作用研究，仅见Suchithra和Koola[15]关于畸形波对单层水平板冲击作用的报道。他们对固定在自由水面的单层水平板，采用含有畸形波的不规则波浪序列与其作用，测试了波浪对结构的冲击压力并给出了压力冲击系数。Suchithra和Koola的试验中得到的畸形波波峰高度与畸形波高之比为0.54，并未完全满足Klinting和Sand[16]给出畸形波定义，因此可以认为该工作仅是畸形波对板式防波堤作用研究的初步尝试。迄今为止尚未见畸形波对双层水平板作用的研究报道。

本文采用物理模型试验方法，系统改变畸形波参数，同步测试双层水平板结构4个受力面的多点波浪压力历时过程，旨在阐释畸形波作用下双层水平板式的压力分布特性，分析畸形波参数对波浪荷载的影响。同时与常规不规则波浪进行比较，解明畸形波与不规则波对双层水平板式防波堤作用之异同。

2 物理模型试验

2.1 试验组别

Klinting和Sand[16]最早提出了畸形波的定义如下：(1)畸形波波高大于有效波高的2倍，即α1=Hj/Hs≥2；(2)畸形波波高大于其前面和后面波浪波高的2倍，即α2=Hj/Hj-1≥2和α3=Hj/Hj+1≥2；(3)畸形波波峰大于波高的0.65倍，即α4=ηj/Hj≥0.65。其中，Hs是波列的有效波高，Hj是畸形波的波高，Hj-1、Hj+1是畸形波前后相邻波浪的波高，ηj是畸形波波高对应的波峰高度。

基于试验目的，将试验组别设计为两大组：(1)畸形波荷载及其特征参数的影响试验；(2)不规则波和畸形波比较试验。试验时，水深固定为0.5m。对畸形波，本质上是一个不规则波序列中出现的异常大波，采用Pei等[17]改进的“三波列叠加模型”方法模拟之(详见试验方法)。模拟时选用JONSWAP谱为输入谱。调整变化α1、α2、α3和α4，指定两种有效波高和5种谱峰周期，得到(1)组的试验参数，见表1。

表1 畸形波荷载试验相关参数汇总

对于(2)组，为了便于畸形波和常规不规则波试验结果的比较，在常规不规则波模拟时，指定畸形波模拟得到的谱为目标谱，同时指定不规则波试验的有效波高和谱峰周期也与畸形波模拟得到的参数完全相同。造波组别参见表2。

表2 不规则波与畸形波对比试验组别参数汇总

2.2 试验设备及模型布置

试验在大连理工大学海岸和近海工程国家重点实验室波流水池中进行，水池长40 m、宽8 m、深1 m。水池前端为美国AOC公司生产的三维推板式多向造波机，可产生试验要求的随机波和畸形波。水池尾部安装有架空斜坡碎石+消能网复合消能设备，以尽量避免波浪的反射。经测试，该消能边界对周期在1.0～1.8 s范围的入射波浪，反射率约3%～5%。

波浪测量采用北京水科院研制生产的DS30型浪高水位仪测量系统，系统内置模/数转换器，巡回采集各通道数据，最小采样时间间隔可达0.001 5 s(约666 Hz)；该系统可同步测量多点波面过程并进行数据分析，标定线性度均大于0.999，测量精度可达毫米级。

波动压力测量采用天津水运科学研究所研制的SG2000型多点压力仪，该系统配置128通道压力数据采集仪，可以实现对点压力过程曲线的多点同步测量，最小采样时间间隔可达0.002 s(500 Hz)；系统具有实时监控、数据采集、数据处理等多项功能，测量精度可达0.1 Pa级。

双层水平板防波堤模型结构如下：板宽B=100 cm，板厚2 cm，板间距S=10 cm，顶高D=50 cm(上层板顶面静水面齐平)，板周围及中间有角钢架加固，用直径2 cm钢管桩固定在基础上，模型整体具有足够的刚度。

为考证水平板防波堤模型存在对畸形波发生位置的影响，将宽8 m的试验水池分隔成宽2 m和6 m两部分(之间砌一宽10 cm分隔墙，墙体前后端均打磨成尖角流线形)。在6 m宽部分，畸形波模拟试验时，在预设水平板防波堤模型中心位置，布置3台波面监测仪，在2 m宽部分同相位位置也布置3台波面监测仪(1台布置在防波堤纵轴线对应的位置上，边缘2台间距与水平板防波堤同宽)。波浪模拟试验结束后，在6 m宽部分布置水平板防波堤模型，但保留2 m宽部分布置的波面监测仪。

双层水平板共有4个受力面，分别称为A1、A2、B1、B2面(A1为上层板上表面，A2为上层板下表面，B1为下层板上表面，B2为下层板下表面)。在每个表面上各安装了9个压力传感器以测定各表面的压力分布(其中，A1受力面压力传感器编号为1#～9#，A2受力面压力传感器编号为10#～18#，B1受力面压力传感器编号为19#～27#，B2受力面压力传感器编号为28#～36#)，各受力面相邻两个压力传感器的中心间距均为0.1 m。试验模型与压力传感器布置详见图1。

图1 物理模型试验布置图及压力盒布置示意图Fig.1 Experimental setup and the twin-plate breakwater layout

2.3 试验及数据分析方法

首先在无模型时进行波浪模拟试验，之后再将双层水平板模型放置于预定位置处进行波浪荷载测试试验。

畸形波模拟采用Pei等[17]改进的“三波列叠加模型”方法，即在计算制作造波信号时，基于同一波谱，把一部分能量分配给一个基本波列，另外一部分配给2个瞬态波列(比1个波列瞬态波列更能增强组成波能量汇聚的效率)，将上述3个波列叠加构成畸形波模拟信号。按照该方法，实现畸形波在水池中的可控制定时、定点生成。

需要说明的是，三波列叠加模型在实现畸形波在水池中的定时、定点生成时，指定了瞬态波列组成波的初始相位，因此不能采用常规波浪的造波方法即造波信号的迭代修正(迭代修正会导致畸形波出现的位置和时间发生变化)，而是一次生成造波信号后，不再进行修正。如果一次生成造波信号生成的波浪序列的统计特性和谱特征参数偏离预定参数较大，则改变基本波列，再出现计算一次性生成造波信号，直到生成的波浪序列的统计特性和谱特征参数与预定参数误差满足要求为止。

为了便于畸形波和常规不规则波试验结果的比较，在常规不规则波模拟时，指定畸形波模拟得到谱型为目标谱型(同时指定有效波高和谱峰周期也与之完全相同)。

试验测量4个受力面所受波浪压力。定义结构受力面受压时波浪压强为正、垂直总力向上为正。垂向总波浪力由4个受力面同步采集到的点压力面积分得到。

试验数据由计算机自动采集，全部试验的波面和点压力参数时间过程自动采集时间窗口相同，均在堤后波浪稳定后开始采集。采样长度均为8 192，采样间隔为0.02 s。每组试验至少重复3遍，取其平均值为试验最终结果。

波浪频谱分析采用FFT方法，3点5遍光滑；试验数据时域统计分析采用常规统计分析方法，其中波高采用上跨零点法。

为方便分析比较，采用ρgHs和ρgHsB2分别对波压力(压强)及单位长总力进行无量纲化处理。其中，ρ为水的比重，g为重力加速度，Hs为有效波高，B为双层水平板板宽。

3 试验结果及分析

3.1 波浪模拟结果

表3、表4汇总给出了试验组别(1)、(2)组的各畸形波列畸形波特征参数及波列统计参数试验结果。

由表3可见，预设畸形波参数α1=2.0～3.0，模拟得到的α1=2.04～3.10; 预设畸形波参数α2≥2.0，模拟得到的α2=1.96～3.30(有1组α2=1.68小于要求的α2≥2.0)；预设畸形波参数α3≥2.0，模拟得到的α3=2.27～4.17；预设畸形波参数α4≥0.65, 模拟得到的α4=0.62～0.75。从模拟得到的畸形波特征参数看，除2组α4=0.62略小于要求的α4≥0.65、1组α2=1.68小于要求的α2≥2.0外，其他参数完全满足畸形波参数定义，从畸形波特征参数角度看，畸形波模拟是较为成功的。

由表4可见，对应不规则波与畸形波对比试验组别，两种波浪的有效波高、谱峰周期及谱面积等参数模拟结果基本一致，为进行不规则波与畸形波对比研究奠定了基础。

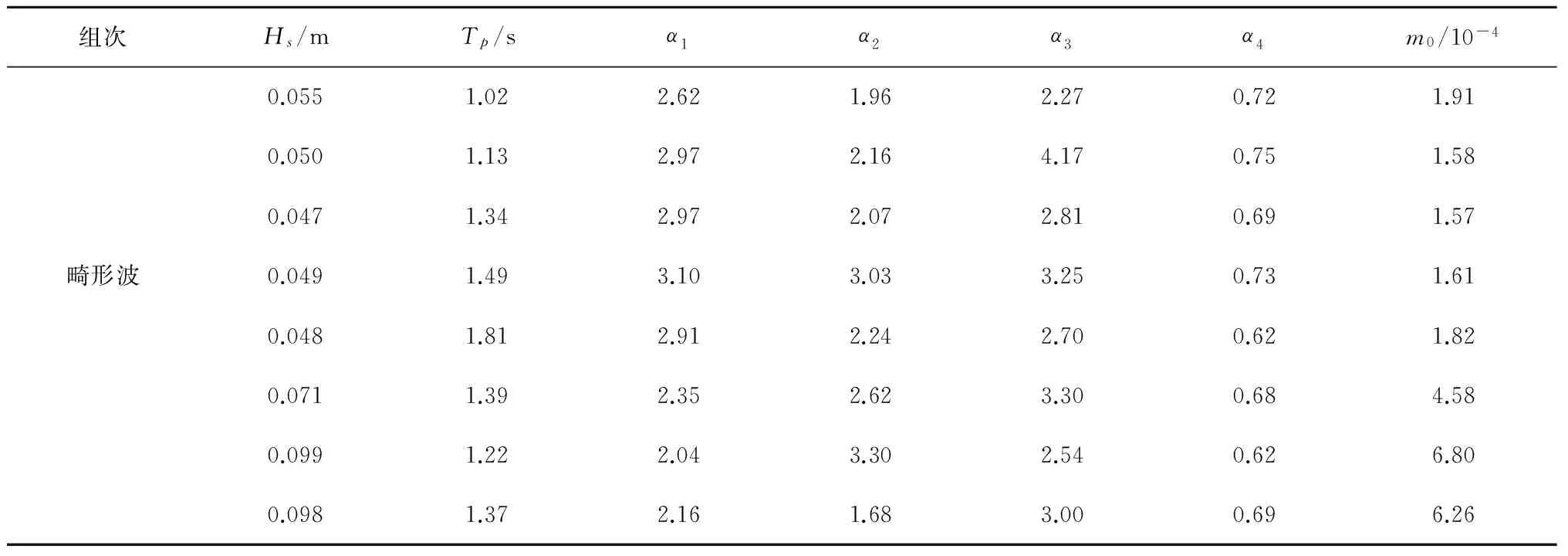
表3 畸形波模拟实测参数汇总

表4 不规则波与畸形波对比试验组别参数汇总

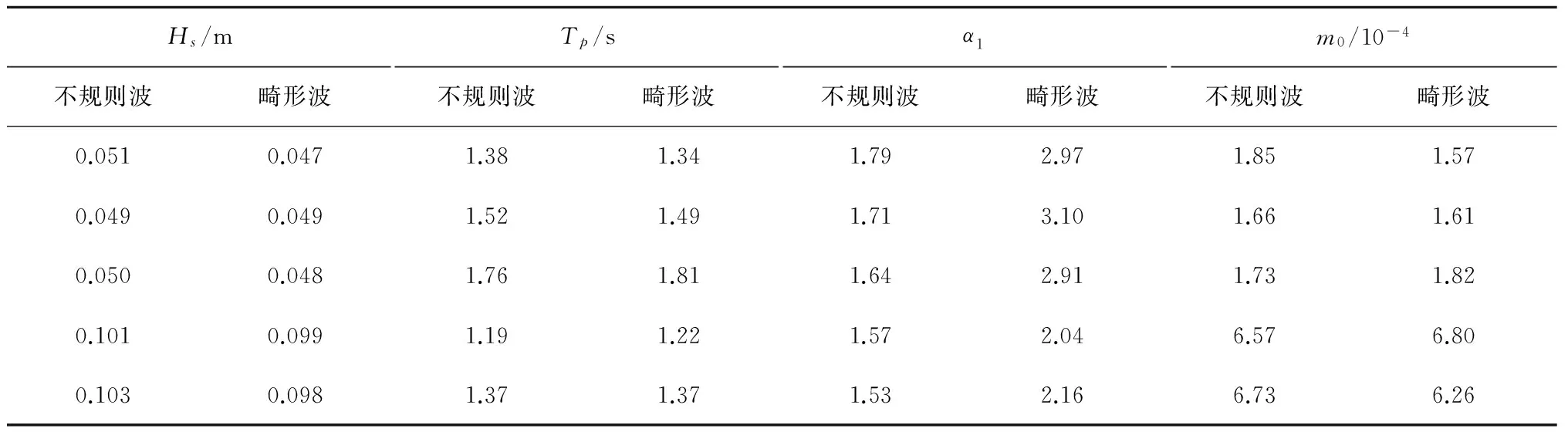
续表4

3.2 畸形波波动压力基本特性

双层水平板共有4个受力面，波浪传播到水平板前端后，受双层水平板作用将发生变形，再进一步向前行进时，水质点运动轨迹不再符合任何波浪理论的描述，且由双层水平板分隔成的3个水域空间(上层板上表面至自由水面空间、双层水平板之间空间、下层板下表面至水底空间)内的水质点运动规律差异很大，双层水平板周围水体的流场结构决定了压力分布形态，显然双层水平板结构的波动压力随时间、空间变化。故研究其压力分布特征应从各不同位置的压力时间过程、同步压力分部、压力包络分布和总力最大时刻的同步波压力分布几个方面分别加以考察。本节首先从双层水平板4个受力面上各不同位置的压力时间过程试验结果出发，讨论畸形波作用下双层水平板结构的压力基本特性；以下各节，将从压力分布及其影响因素角度，全面探讨畸形波作用下双层水平板结构的波浪荷载特性和变化规律。

图2给出了两组不同相对板宽条件下，畸形波作用时，双层水平板4个受力面(A1、A2、B1、B2表面)不同位置(每个受力面上分别选取前端、中间、后端3个代表点)的点压力及其对应的畸形波波列历时过程试验曲线示例。

图2a对应的相对板宽较窄的情况，该组别试验参数为：相对板宽B/L=0.28，相对波高Hs/D=0.1；畸形波参数为：畸形波的周期和波长分别为TF=2.02 s，LF=4.1 m，α1=2.9，α2=2.2，α3=2.7，α4=0.62。波列参数为Hs=0.05 m，Tp=1.8 s；图2b对应的相对板宽较宽的情况，该组别的试验参数为：相对板宽B/L=0.66，相对波高Hs/D=0.1；畸形波参数为：畸形波的周期和波长分别为TF=1.12 s，LF=1.83 m，α1=2.6，α2=2.0，α3=2.27，α4=0.71。波列参数为Hs=0.05 m，Tp=1.0 s。

从图2a可见，对应较窄相对板宽的情况，畸形波出现在20～22 s时段区间。在该区间内，双层水平板4个受力面波动压力达到最大值非同步但可谓准同步，最大波动压力出现在水平板中前区域。

其中，双层水平板前端(4个受力面的测点分别为1#、10#、19#、28#)，上层板上表面(A1面)在20.26 s时刻出现最大压力，Pmax=1.01 kPa；上层板下表面(A2面)在20.18 s时刻出现最大压力，Pmax=1.04 kPa；下层板上表面(B1面)在20.24 s时刻出现最大压力，Pmax=0.75 kPa；下层板下表面(B2面)在20.08 s时刻出现最大压力，Pmax=0.54 kPa；双层水平板前端区域，4个受力面波动压力达到最大值的时间差Δt≤0.18 s≈Tp/10≈TF/11。

比较双层水平板4个受力面的波动压强可见，最大压强出现在上层板上，且上层板上、下表面波动压力最大值非常接近；下层板上、下表面波动压力最大值小于上层板的。下层板上表面出现最大压力大于下层板下表面的最大压力。双层水平板中间位置(4个受力面的测点分别为5#、14#、23#、32#)，A1面在20.58 s时刻出现最大压力，Pmax=0.48 kPa；A2面在20.14 s时刻出现最大压力，Pmax=0.72 kPa；B1面在20.3 s时刻出现最大压力，Pmax=0.585 kPa；B2面在20.24 s时刻出现最大压力，Pmax=0.353 kPa。双层水平板中间区域4个受力面波动压力达到最大值的时间差Δt≤0.44 s≈Tp/4≈TF/5。显然双层水平板中间区域4个受力面波动压力达到最大值的时间差大于前端区域的时间差。

与前端不同，双层水平板中间4个受力面的最大压强出现在上层板下表面。双层水平板后端(4个受力面的测点分别为9#、18#、27#、36#)，A1面在20.7 s时刻出现最大压力，Pmax=0.478 kPa；A2面在20.34 s时刻出现最大压力，Pmax=0.376 kPa；B1面在20.26 s时刻出现最大压力，Pmax=0.351 kPa；B2面在20.3 s时刻出现最大压力，Pmax=0.294 kPa；双层水平板后端区域4个受力面波动压力达到最大值的时间差Δt≤0.44 s≈Tp/4≈TF/5，与中间区域的时间差基本相同。

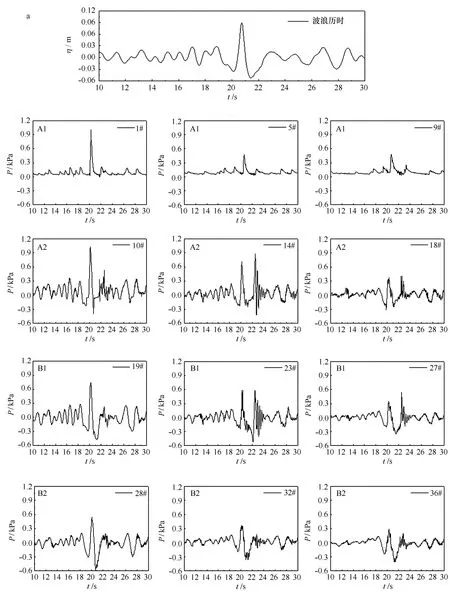
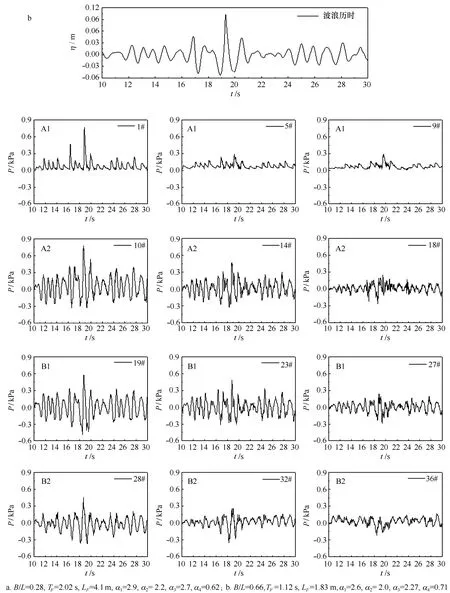
图2 波列及结构4个受力面代表点波压历时示例(Hs/D=0.1)Fig.2 The time series of freak waves and the wave pressure of the four surfaces (Hs/D=0.1)

从图2b(较宽相对板宽时)可见，畸形波出现在18.5～20.5 s时段区间。该时段区间内，双层水平板4个受力面波动压力达到最大值时刻也是非同步的。

双层水平板4个受力面前端区域(测点1#、10#、19#、28#)，A1面最大压力出现在18.86 s，Pmax=0.768 kPa；A2面出现在18.72 s，Pmax=0.777 kPa；B1面出现在18.76 s，Pmax=0.576 kPa；B2面在出现18.68 s，Pmax=0.451 kPa；4个受力面波动压力达到最大值的时间差Δt≤0.18 s≈Tp/5≈TF/6。

双层水平板中间区域(测点5#、14#、23#、32#)，A1、A2、B1、B2 4个受力面出现最大压力的时间分别在19.22 s、18.82 s、18.8 s和19.02 s，对应的最大压力分别为Pmax=0.288 kPa、0.471 kPa、0.486 kPa和0.259 kPa；4个受力面波动压力达到最大值的时间差Δt≤0.42 s≈0.4Tp。

双层水平板后端区域(测点9#、18#、27#、36#)，A1、A2、B1、B2 4个受力面出现最大压力的时间分别在19.66 s、19.54 s、19.38 s和19.44 s，对应的最大压力分别为Pmax=0.287 kPa、0.251 kPa、0.29 kPa和0.166 kPa；4个受力面波动压力达到最大值的时间差Δt≤0.28 s≈0.3Tp。

综合比较两种相对板宽(B/L=0.28和0.66)条件下波动压力试验结果可以看出：(1)双层水平板最大波动压力出现在畸形波发生的时段内；(2)最大波动压力出现位置在前端迎浪区域附近，向尾端逐渐递减；(3)对于平顶堤，A1面波动压力历时过程无负值(无波吸力)，A2和B1面波压力显著大于波吸力，B2面波压力和波吸力强度大体相当；(4)畸形波对双层水平板作用，主要体现在水平板前区A1、A2和B1 3个受力面上；(5)4个受力面的最大波动压力非同步，最大时间差与相对板宽有关，本试验范围内，双层水平板4个受力面的最大波动压力时间差约在0.1Tp～0.4Tp范围内变化。

3.3 同步波动压力分布特性

同步波浪压力是计算水平板波浪总力的基础，在此讨论双层水平板同步波浪压力分布特征，对认识和掌握水平板波浪总力的变化规律具有基础性意义。

如前所述，双层水平板4个受力面的波动压力有所不同，此外，同步波浪压力分布形态相对相位(时刻)有关。下面选取4个具有代表性的相对相位(时刻)进行讨论。4个时刻分别为双层水平板总垂向力最大时刻和上层板上表面前、中、后位置出现最大波动压力时刻。

图3给出的是双层水平板垂向总力最大时刻，4个受力面的同步波压力分布实测结果示例。图中，横坐标为水平板相对位置(沿波浪传播方向，迎浪端为0，尾端为1)，纵坐标为无因次波动压力(p/ρgHs)。试验条件为：TF=2.02 s,LF=4.1 m, α1=2.9，α2=2.2，α3=2.7，α4=0.62，Hs=0.05 m，Tp=1.8 s，Hs/D=0.1，B/L=0.28。

由图3a可见，(1)在向上的总垂向力(也可称为浮托力)最大时刻(t=20.06 s)，两个受力的下表面(A2和B2面)的波压力较两个受力的上表面(A1和B1面)的大，向上的总垂向力主要源于两个下表面(A2和B2面)的贡献，而两个上表面(A1和B1面)对向上的总垂向力的贡献为负值；(2)在该时刻，A2、B2、B1 3个受力面的同步波压力分布由迎浪端向尾端逐渐减小，而A1面的波压力分布由迎浪端向尾端逐渐增大。

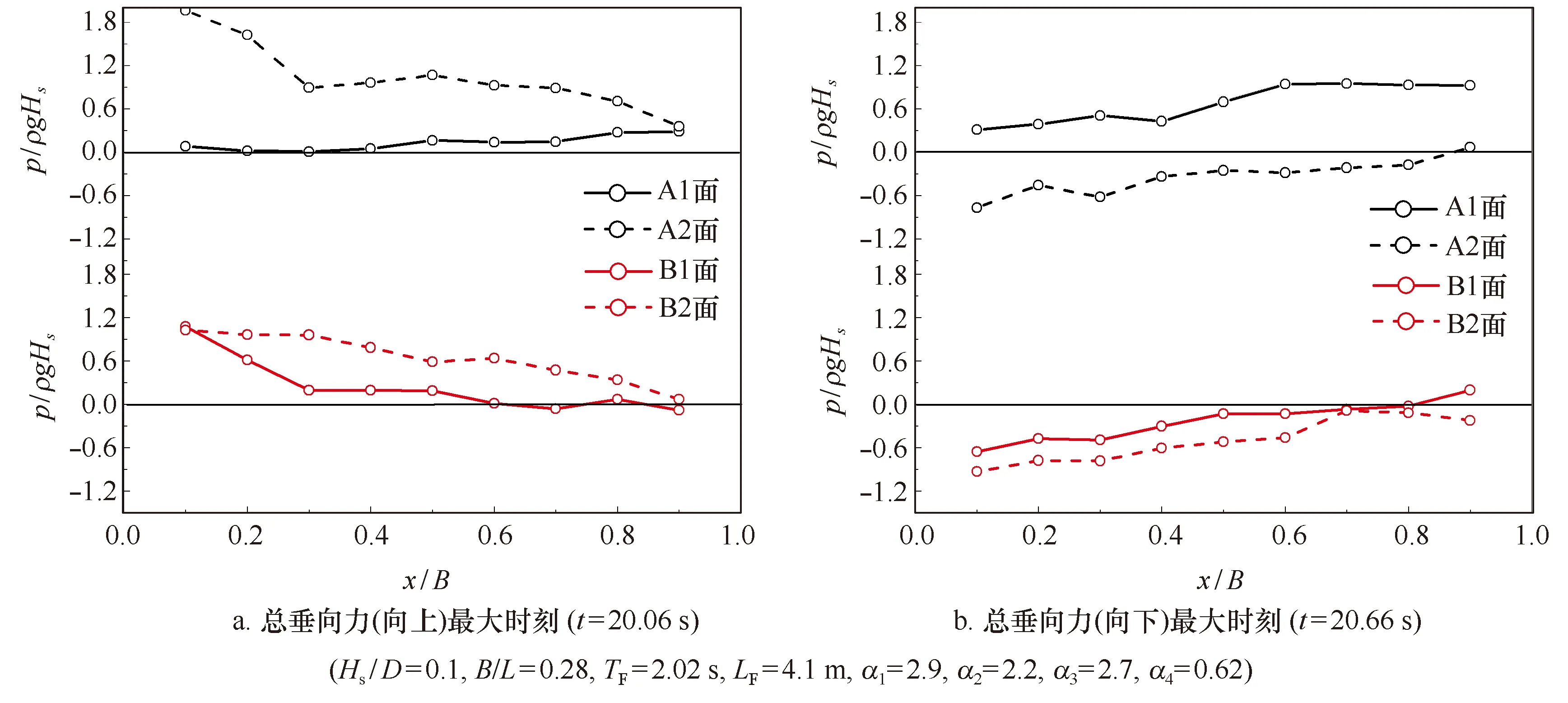
图3 总垂向力最大时刻的同步波压力分布结果示例Fig.3 The distribution of synchronous wave pressure at the moment of maximum total force

由图3b可见，(1)在向下的总垂向力最大时刻(t=20.66 s)，有3个受力面(B1、A2和B2面)的波动压力为负值，即为波吸力，仅有A1面为正值；(2)注意到不同受力面的朝向，可以判断出向下的总垂向力源于A1、A2和B2面3个受力面的贡献，此时B1面对向下的总垂向力的贡献为负值；(3)在该时刻，B1、A2和B2面的压力绝对值由迎浪端向尾端逐渐减小，而A1面的波压力分布由迎浪端向尾端方向(至x/B≈0.7)先增大然后(x/B=0.7～1)基本不变。

由总垂向力最大时刻的同步波动压力分布形态可以认为，工程最关注的双层水平板总浮托力主要源于双层板的两个下表面。

图4a～c分别给出了与图3相同试验条件下，双层水平板上层板上表面前、中、后位置出现最大波动压力时刻，4个受力面的同步波压力分布实测结果示例。

图4 代表性相对相位(时刻)的同步波压力分布结果示例Fig.4 The distribution of synchronous wave pressure at the moment of typical relative phases

图4a可见，上层板上表面前端波动压力最大时刻(t=20.26 s)，4个受力面全都受压，A1面受到的压力由迎浪端向中部迅速减小，在x/B=0.4～1区域无因次波动压力不超过0.188，仅为迎浪端最大压力的10%；A2、B1、B2 3个受力面波动压力沿波浪传播方向总体上均呈递减趋势。其中，A2面波动压力最大，B1面次之，B2面再次之。另应注意到，B1面在x/B=0.7处出现异常波动，表明下层板上表面在该位置附近的流场形态有变化。受力由迎浪端向尾端波动分布，而受压沿表面分布均匀。

图4b可见，上层板上表面中间位置波动压力最大时刻(t=20.58 s)，仅有A1面波动压力同向(受压)且该受力面中间附近区域(x/B=0.4～0.7区域)受力较大而两端较小，其他3个受力面波动压力方向均有变向情况发生(波压力和波吸力同时发生，但波动压力强度不大)。需要注意到A2面出现波吸力与波压力交替多次情况，表明A2面附近水域流场变化较为复杂。

图4c可见，上层板上表面尾端位置波动压力最大时刻(t=20.7 s)，A1面仍然全部受压，由前至后呈递增趋势；其余3个受力面均呈波吸力作用(仅见B1面在尾端局部区域出现很小的压力)，波吸力由前至后呈递减变化。

图4a～c的试验结果总体上代表了畸形波由双层水平板前端传播至尾端整个过程中，不同受力面同步波浪压力分布的随相对相位的变化过程。在该过程中：

上层板上表面(A1面)一直呈受压状态，压力强度随畸形波波峰作用达到峰值；

上层板下表面(A2面)在畸形波波峰作用到水平板前端时呈全面受压状态，最大压力强度可达到A1面最大压力水平；畸形波波峰作用达到水平板中间时，出现波吸力与波压力交替多次情况，压力强度则大大降低；畸形波波峰作用达到水平板尾端时，上层板下表面呈全面受波吸力状态，波吸力沿波浪传播方向呈递减趋势，最大波吸力强度与该时刻A1面上最大压力强度大体相当。

下层板上表面(B1面)在畸形波波峰作用到水平板前端时呈全面受压状态，压力强度小于A2面压力强度；畸形波波峰作用达到水平板中间时，出现波压力与波吸力交替情况，压力强度则大大降低；畸形波波峰作用达到水平板尾端时，该面呈全面受波吸力状态，波吸力沿波浪传播方向呈递减趋势。

下层板下表面(B2面)在畸形波波峰作用到水平板前端时呈全面受压状态，压力强度小于A2面压力强度；畸形波波峰作用达到水平板中间时，压力分布与B1面基本相同；畸形波波峰作用达到水平板尾端时，该面呈全面受波吸力状态，压力分布与A2面基本相同。

比较图3和图4可见，双层水平板结构(向上或向下)的总垂向力最大时刻与上层板上表面波动压力最大时刻是不一致的：双层水平板结构向上的总垂向力(浮托力)最大时刻，比上层板上表面最前端出现最大波动压力时刻提前(相差0.2 s)；向下的总垂向力最大时刻，比上层板上表面最尾端出现最大波动压力时刻提前(相差0.04 s)。就双层水平板结构的总垂向力(向上或向下)最大时刻同步波动压力分布形态而言，浮托力最大时刻的同步波动压力分布形态与上层板上表面前端波动压力最大时刻的同步波动压力分布形态接近：向下的总垂向力最大时刻同步波动压力分布形态则与上表面尾端波动压力最大时刻的同步波动压力分布形态类似。

3.4 波动压力包络分布特性

波压力的包络分布最直观反映出结构表面各位置所受到的最大波压力情况。

图5a～d分别给出了相对波高固定(Hs/D=0.1)时，4种不同相对板宽(B/L=0.28，0.39，0.5，0.66)条件下，双层水平板各表面的无因次压力包络分布试验结果示例。

总体而言，在相对板宽B/L=0.28～0.66的试验范围内，相对板宽对波压力包络分布无显著影响；同时，波压力包络分布呈由迎浪端向尾端逐渐减小的趋势。就不同受力面而言，波压力包络分布则呈现出不同特点：A1受力面，负向波压力(波吸力)接近0，正向波压力显著大于波吸力；A2和B1受力面，正向波压力和波吸力分布形态近似，同时正向波压力略大于负向波压力；B2受力面，正负波压力强大基本相当，有时波吸力略大于波压力。

4 畸形波与不规则波作用的比较

如前所述，为了便于畸形波和常规不规则波试验结果的比较，在常规不规则波模拟时，指定畸形波模拟得到的谱为目标谱，同时指定的有效波高和谱峰周期也与畸形波模拟得到的参数完全相同(参见试验组别表2)。在上述条件下，分别对畸形波和常规不规则波作用下双层水平板的波压力包络分布、结构总垂向力进行比较分析，以明确其异同。

4.1 波压力包络分布比较

在此，以两组不同相对板宽(B/L=0.28，0.66)试验结果为例，比较畸形波和不规则波作用时，双层水平板4个受力面的波压力包络分布情况。试验结果分别参见图6和图7。

图6给出的是畸形波和不规则波相对波高均为Hs/D=0.1，谱峰周期均为Tp=1.8 s、B/L=0.28时的试验结果。图中可见，畸形波和不规则波作用时，双层水平板4个受力面的波压力包络分布特征基本一致，但从波动压力强度看，除A1受力面的波吸力接近(均接近0，平顶堤的缘故)外，畸形波作用下4个受力面的波压力包络均显著大于不规则波作用时的波压力包络值。图7(畸形波和不规则波相对波高均为Hs/D=0.1，谱峰周期均为Tp=1.0 s、B/L=0.66)也显示了与图6相同的结果。

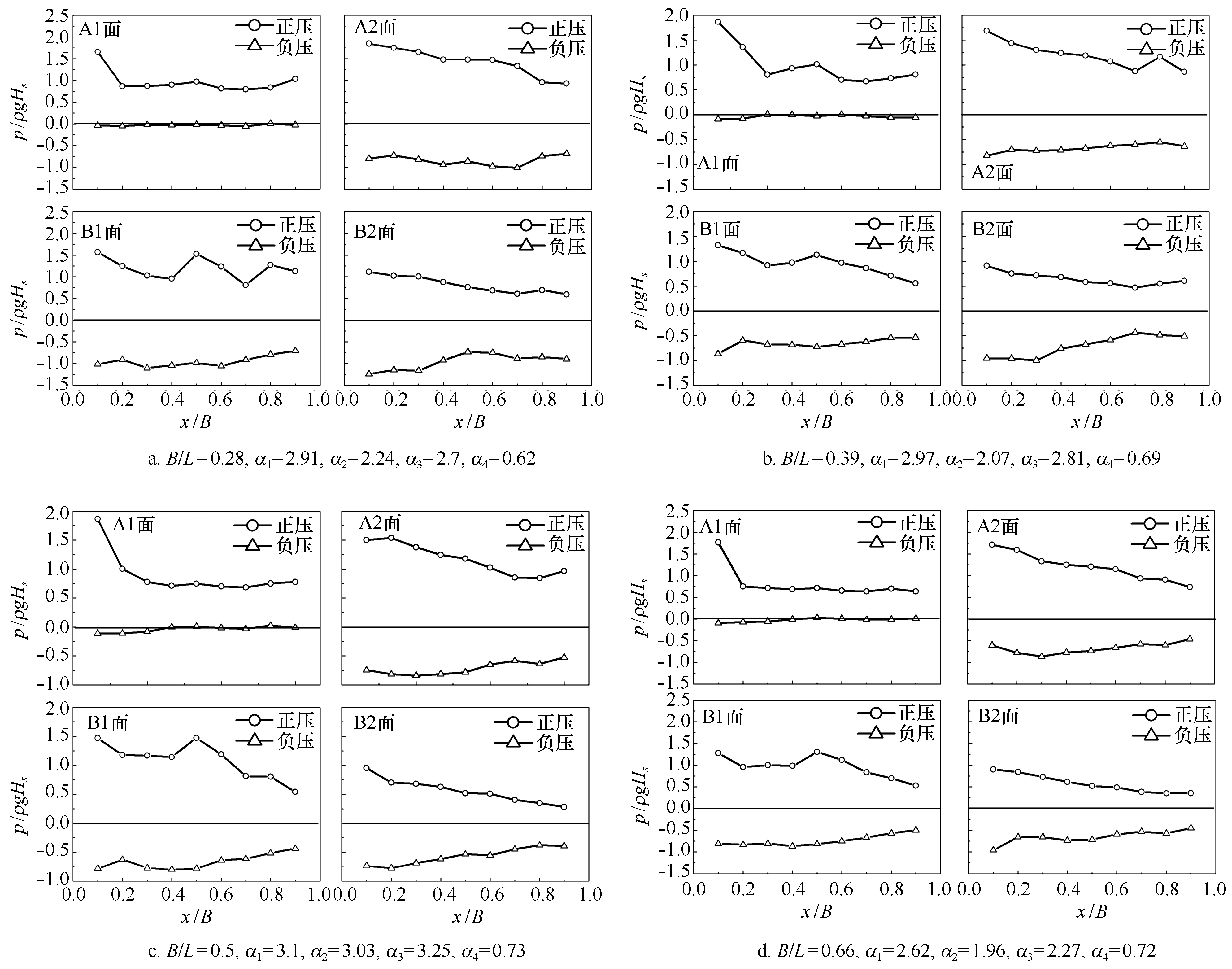
图5 畸形波作用下双层水平板各受力面正负波压力包络分布示例(Hs/D=0.1)Fig.5 The maximum pressure of the twin-plate breakwater under freak waves

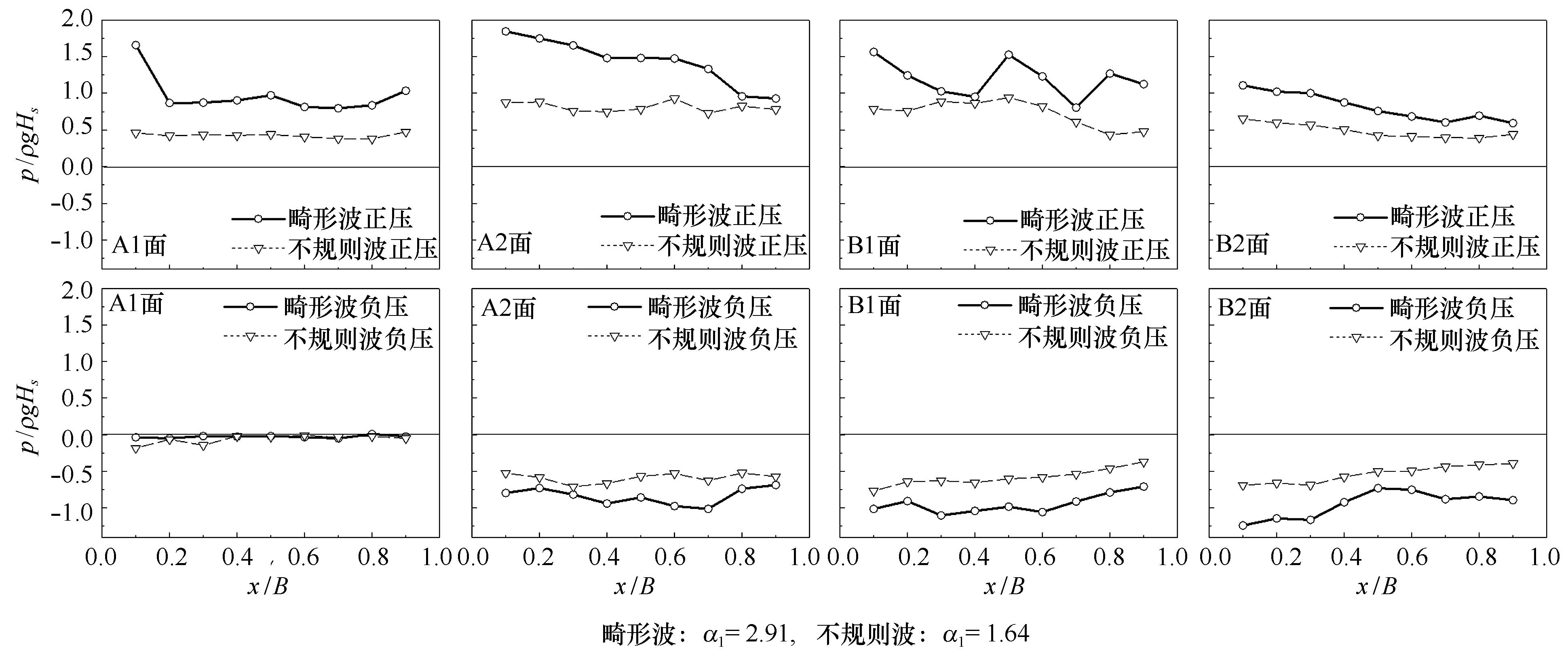
图6 畸形波与不规则波的作用下双层水平板结构压力包络的对比结果(B/L=0.28)Fig.6 Comparison of the maximum pressure result with irregular waves (B/L=0.28)

图7 畸形波与不规则波的作用下双层水平板结构压力包络的对比结果(B/L=0.66)Fig.7 Comparison of the maximum pressure result with irregular waves (B/L=0.66)

图8 畸形波和不规则波作用时最大压强比试验结果Fig.8 The maximum pressure ratio between freak waves and irregular waves

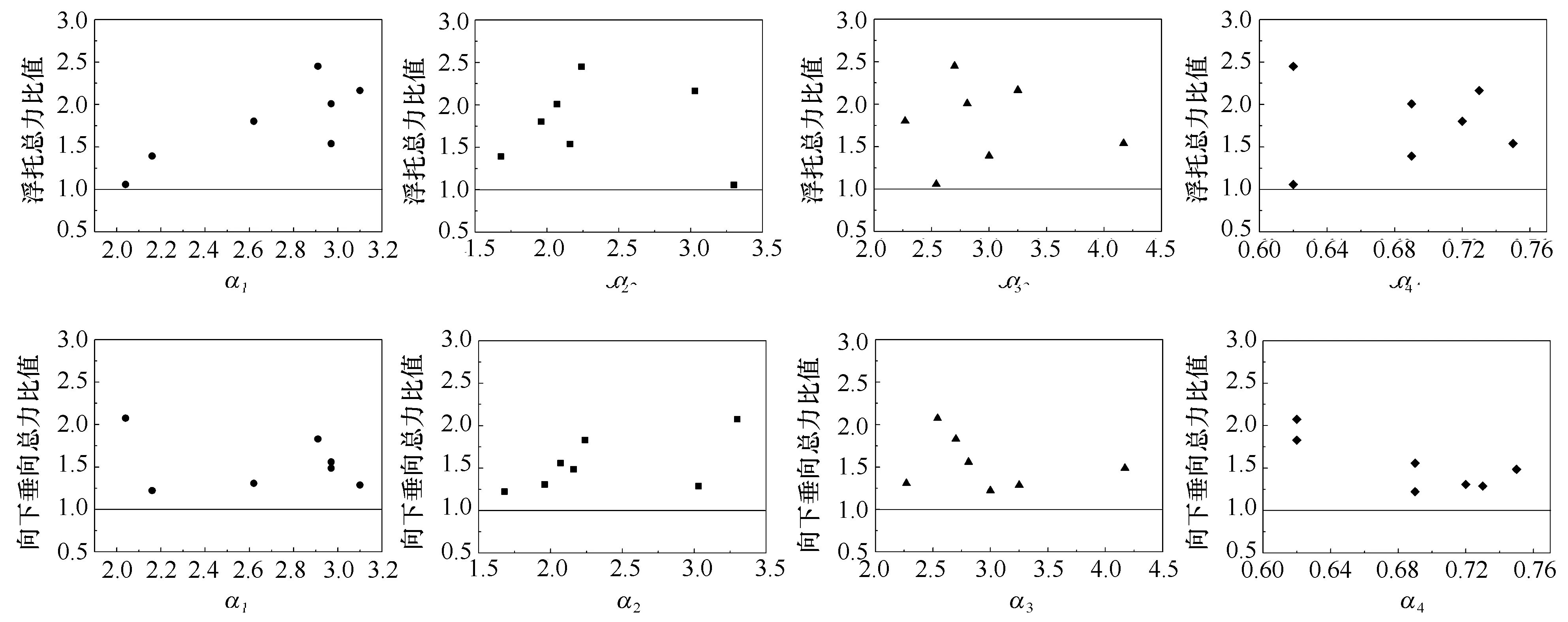
图9 畸形波和不规则波作用时最大总力比试验结果Fig.9 The maximum total vertical force ratio between freak waves and irregular waves

由此可认为，与不规则波作用比较，畸形波作用没有改变波压包络分布特征，但增大了波压包络强度值。

4.2 最大压强值对比

从前节给出的畸形波和不规则波作用时双层水平板4个受力面的波压力包络比较发现，畸形波作用时增大了双层水平板4个受力面波压强度。为了定量分析，在此选择4个受力面中出现的最大压强值进行对比。显然，畸形波作用时，4个受力面中出现的最大压强值可能与畸形波参数(α1、α2、α3、α4)有关，故在此给出所有受力面中最大压强的比值随畸形波参数变化的试验结果。

图8给出了畸形波参数α1=2.04～3.1、α2=1.68～3.3、α3=2.27～4.17、α4=0.62～0.75，相对板宽B/L=0.28～0.66，相对波高Hs/D=0.1～0.2的试验范围内，最大压强的比值随畸形波参数(α1、α2、α3、α4)变化的试验结果。

由图8可见，畸形波作用时，双层水平板结构最大波压力显著大于不规则波作用时的最大波压力，其增大的幅度与畸形波参数α1相关性最强，随α1的增大而增大，在α1=2.04～3.1试验范围内，最大压强的比值在1.21～1.81范围内变化，即畸形波作用时的最大压强比不规则波作用时可约增大20%～80%。畸形波作用时，双层水平板结构最大波吸力不一定大于不规则波作用时的最大波吸力，两者的比值与畸形波参数α4相关性最强，随α4的增大而减小。在α4=0.62～0.75试验范围内，最大波吸力强度的比值在1.61～0.87范围内变化。当α4≤0.72时，畸形波作用时的最大波吸力大于不规则波作用时的最大波吸力；当α4>0.72时则刚好相反。此外从图中还可以看出，畸形波参数α2和α3对畸形波和不规则波作用时的最大压强的比值影响无显著规律，对此应进一步研究。

4.3 最大垂向总力的比较

图9给出了畸形波与不规则波作用下，双层水平板结构最大垂向总力比值随畸形波参数(α1、α2、α3、α4)变化的试验结果。图中可见，与不规则波作用相比，畸形波作用时下双水平板结构所受总力要大很多，无论浮托总力还是向下垂向总力，二者比值都大于1。与最大压强随畸形波参数变化趋势类似，双层水平板结构最大浮托总力与畸形波参数α1相关性较其他参数略强，而向下最大垂向总力随畸形波参数α4变化的趋势最明显。总体而言，畸形波4个参数联合影响了双层水平板结构总力。

试验范围内，结构最大浮托总力比值在1.06～2.45间变化；向下最大垂向总力比值在1.22～2.07之间变化。

5 结论

基于畸形波和不规则波对双层水平板式防波堤作用的物理模型试验，考虑畸形波参数、相对板宽、相对波高等影响因素，对畸形波作用下双层水平板式防波堤波浪力分布特征进行了讨论，并就最大波动压强、结构最大垂向总力进行了畸形波与不规则波作用的对比分析，得到以下认识：

畸形波作用下，平顶的双层水平板波压力分布具有以下基本特征：(1)双层水平板最大波动压力出现在畸形波发生的时段内；(2)最大波动压力出现位置在前端迎浪区域附近，向尾端逐渐递减；(3)上层板上表面波动压力历时过程无负值(无波吸力)，上层板下表面和下层板上表面波压力显著大于波吸力，下层板下表面B2面波压力和波吸力强度大体相当；(4)4个受力面的最大波动压力非同步，最大时间差与相对板宽B/L有关，本试验范围(B/L=0.28～0.66)内，双层水平板4个受力面的最大波动压力时间差约在0.1Tp～0.4Tp范围内变化。

与不规则波作用比较，畸形波作用没有改变波压包络分布特征，但增大了波压包络强度值。就波动压力而言，其增大的幅度与畸形波参数α1相关性最强，随α1的增大而增大，在α1=2.04～3.1试验范围内，最大压强的比值在1.21～1.81范围内变化，即畸形波作用时的最大压强比不规则波作用时可约增大20%～80%。就最大波吸力而言，两者的比值与畸形波参数α4相关性最强，随α4的增大而减小。在α4=0.62～0.75试验范围内，最大波吸力强度的比值在1.61～0.87范围内变化。当α4≤0.72时，畸形波作用时的最大波吸力大于不规则波作用时的最大波吸力；当α4>0.72时则刚好相反。

与不规则波作用相比，畸形波作用时下双水平板结构所受总力要大很多，无论浮托总力还是向下垂向总力，二者比值都大于1。试验范围内，结构最大浮托总力比值在1.06～2.45间变化；向下最大垂向总力比值在1.22～2.07之间变化。

畸形波参数α1～α4联合影响了其对双层水平板作用总力，仅就单一因素考察难以发现其规律，对此应进一步研究。

[1] Sand S E, Hansen N E O, Klinting P, et al. Water Wave Kinematics[M]. Netherlands: Springer, 1990: 535-549.

[2] Chien H W A, Kao C C. On the characteristics of observed coastal freak waves[J]. Coastal Engineering Journal, 2002, 44(4): 301-319.

[3] Melville W K. Energy dissipation by breaking waves[J]. Journal of Physical Oceanography, 1994, 24: 2041-2049.

[4] Mori N, Liu P C, Yasuda T. Analysis of freak wave measurements in the sea of Japan[J]. Ocean Engineering, 2002, 29(11):1399-1414.

[5] Nikolkina I, Didenkulova I. Rogue waves in 2006-2010[J]. Natural Hazards and Earth System Science, 2011, 11(11): 2913-2924.

[6] Haver S. A possible freak wave event at measured at the Draupner Jacket January 1 1995[M]//Proceeding of Rogue Waves, Brest, France, 2004.

[7] Patarapanich M, Cheong H F. Reflection and transmission characteristics of regular and random waves from a submerged horizontal plate[J]. Coastal Engineering, 1989, 13(2): 161-182.

[8] Cheong H F, Patarapanich M. Reflection and transmission of random waves by a horizontal double-plate breakwater[J]. Coastal Engineering, 1992, 18(1/2): 63-82.

[9] Liu P L F, Iskandarani M. Scattering of short-wave groups by submerged horizontal plate[J]. Journal of Waterway Port Coastal and Ocean Engineering, 1991, 117(3): 235-246.

[10] Usha R, Gayathri T. Wave motion over a twin-plate breakwater[J]. Ocean Engineering, 2005, 32(8/9)：1054-1072.

[11] Neelamani S, Gayathri T. Wave interaction with twin plate wave barrier[J]. Ocean Engineering, 2006, 33(3): 495-516.

[12] Liu Yong, Li Yucheng, Teng Bin, et al. Wave motion over two submerged layers of horizontal thick plates[J]. Journal of Hydrodynamics, 2009, 21(4): 453-462.

[13]唐琰林，张宁川，刘爱珍. 双层水平板型透空式防波堤消波性能试验研究[J]. 水道港口, 2006, 27(5):284-288.

Tang Yanlin, Zhang Ningchuan, Liu Aizhen. Test on wave-dissipating performance of twin-plate penetrating breakwater[J]. Journal of Waterway and Harbour, 2006, 27(5):284-288.

[14] 李靖波. 双层水平板防波堤水动力特性研究[D]. 大连: 大连理工大学, 2014.

Li Jingbo. The study of hydrodynamic performance of twin-plate breakwater[D]. Dalian: Dalian University of Technology, 2014.

[15] Suchithra N, Koola P M. A study of wave impact on horizontal slabs[J]. Ocean Engineering, 1995, 22(7): 687-697.

[16] Klinting P, Sand S E. Analysis of Prototype Freak Waves[R]. Conference on Nearshore Hydrodynamics, ASCE. Washington, 1987: 618-362.

[17] Pei Yuguo, Zhang Ningchuan, Zhang Yunqiu, et al. Efficient generation of freak waves in laboratory[J]. China Ocean Engineering, 2007, 21(3): 515-523.

Experimental study on wave pressure distribution of the twin-plate breakwater under freak waves

Gu Qian1, Zhang Ningchuan1

(1.StateKeyLaboratoryofCoastalandOffshoreEngineering,DalianUniversityofTechnology,Dalian116024,China)

This study carried out extensive experiments to investigate the wave loads on the twin-plate breakwater under freak waves. The characteristics of wave forces were checked under various relative plate width, relative wave height as well as freak waves parameters. The results show that the maximum wave pressure occurred on the offshore side of the twin-plate, and decreased along the wave propagating direction. The wave pressures on the four surfaces of the twin-plate showed significant difference in both magnitude and phase, and the phase difference ranged in 0.1Tp～0.4Tp. In addition, the measured maximum wave pressure and total vertical force on the twin-plate were compared to those under irregular waves. There is no significant difference in the distribution of the wave pressure envelop for irregular and freak waves. However, the magnitude under freak waves is significant larger than that under irregular waves. Basically, the ratio of the maximum total uplift forces for under freak waves to irregular waves ranges in 1.06-2.45; the ratio of the maximum downward vertical force ranges in 1.22 to 2.07. The increment of the maximum wave pressure is subjected to the freak waves parameterα1.Withα1from 2.04 to 3.1, the maximum pressures under freak waves can be 20% to 80% larger than those under irregular waves. The ratio of the maximum wave suction force between the irregular and freak waves is decreased withα4. Withα4=0.62-0.75, the ratio of the maximum wave suction force changes from 1.61 to 0.87. It should be noted that, the critical value ofα4turns out to be 0.72, below which the maximum wave suction forces under freak waves are larger than those under irregular waves, and above which is the other way round.

freak wave; twin-plate breakwater; wave loads; model test

10.3969/j.issn.0253-4193.2017.05.012

2016-06-29；

2016-08-17。

国家自然科学基金(51079025)。

顾倩(1985—)，女，辽宁省大连市人，博士生，主要从事波浪与双层水平板结构研究。E-mail:kaosaiqian@126.com

*通信作者：张宁川，男，教授，主要从事波浪与海洋结构物研究。E-mail:nczhang@126.com

P731.22

A

0253-4193(2017)05-0123-15

顾倩, 张宁川. 畸形波作用下双层水平板防波堤压力分布特性研究[J]. 海洋学报,2017,39(5): 123-137,

Gu Qian, Zhang Ningchuan. Experimental study on wave pressure distribution of the twin-plate breakwater under freak waves[J]. Haiyang Xuebao, 2017,39(5): 123-137, doi：10.3969/j.issn.0253-4193.2017.05.012