强非线性和色散性Boussinesq方程数值模型检验

赵红军, 焦影霞, 孔俊

(1.河海大学 港口海岸与近海工程学院, 江苏 南京 210098)

强非线性和色散性Boussinesq方程数值模型检验

赵红军1, 焦影霞1, 孔俊1

(1.河海大学 港口海岸与近海工程学院, 江苏 南京 210098)

采用同位网格有限差分法，建立了强非线性和色散性Boussinesq方程数值计算模型。以稳恒波Fourier近似解给定入射波边界条件，对均匀水深深水和浅水域不同非线性的行进波、缓坡地形上深水至浅水域的浅水变形波、以及缓坡和陡坡地形上的波浪水槽实验进行了数值计算，并将计算结果与解析解、解析数值解以及实验值进行了较为详细的比较，从而检验了模型的色散性、非线性以及不同底坡下非线性波的浅水变形性能。

Boussinesq方程；非线性；色散性；浅水变形

1 引言

Boussinesq型方程是研究近岸水域波浪传播变形的一个有力工具，虽然均匀水深水域下的Boussinesq方程[1]早在1872年就已给出，此类方程的实际应用却始于1960年代变水深水域经典Boussinesq方程[2]的导得。因经典Boussinesq方程仅具弱色散性和弱非线性，且未考虑水底摩阻和近岸波浪破碎的影响，所以自20世纪80年代始针对Boussinesq方程的研究主要集中在方程色散性和非线性的提高以及向近岸破波区的推广。

在色散性能方面，Witting[3]首先引入了Padé近似和伪速度的概念，有力推动了Boussinesq型方程色散性能的改进。受Padé近似的启发，Madsen等[4]在动量方程中引入系数待定的三阶导数项，得到了色散关系改进型Boussinesq方程。Nwogu[5]推导了以任意层水平速度为特征速度的Boussinesq方程。任意层速度的引入不但提高了方程的色散性能，而且优化了波动水质点速度的垂向分布，这在Gobbi及其合作者[6-7]以两层水平速度势函数重构特征速度的理论研究中有着较好的体现。上述Boussinesq方程的改进多以提高方程偏微分的阶数为代价(如高至五阶[7])，这为数值求解工作带来了极大困难，为此，Lynett和Liu[8-9]引入了垂向分层的概念，他们以两层或多层水平速度为特征速度表达的方程，在提高色散性能的同时还达到了偏微分降阶的目的(降低至三阶)。后来，Chazel等[10]进一步将两层Boussinesq方程偏微分的阶数降低至两阶；Liu和Fang[11]的工作进一步拓宽了两层Boussinesq方程的水深适用范围。

在非线性性能方面，早期的改进方式主要是摒弃弱非线性假设，保留与色散项同阶的所有非线性项，由此产生了所谓的“完全非线性Boussinesq方程”[12—13]；也有学者引入随空间和时间变化的任意水深层概念[13—14]，以优化该类方程的非线性性能。尽管早期的改进工作在某些方面一定程度上提高了方程的非线性性能，但在水深较大时方程的非线性精度还远不及线性特征。Agnon等[15]在非线性改进方面做出了富有成效的工作：他们基于Laplace方程和水底边界条件，通过Padé近似和算子运算技术，得到了静水面水平速度和垂向速度之间的关系；以自由面速度和自由面为特征变量，表示自由面运动学和动力学边界条件；通过速度势级数展式建立自由面速度变量和静水面速度变量之间的关系，从而给出了另一类形式的Boussinesq方程(称之为Agnon型Boussinesq方程)。此后，Madsen等[16]通过算子运算技术引入任意层伪速度，进一步优化提高了该类Boussinesq方程的色散性和水质点速度的垂向分布；Wang等[17]通过任意层速度、Zhang等[18]通过任意层伪速度，分别给出了显含定常背景水流影响的Agnon型Boussinesq方程。

尽管Agnon型Boussinesq方程具有良好的色散性能、变浅性能和非线性性能，但是繁杂的表达形式及其包含的高阶导数项为方程的数值求解带来了困难。Fuhrman和Bingham[19]构建了空间七点差分、时间四阶Runge-Kutta向前步进的计算格式，对以任意层伪速度为特征速度的方程[16]进行了数值求解；张洪生等[20]通过空间七点差分、时间五阶Runge-Kutta-England向前步进的格式，数值求解了以任意层速度为特征速度的方程[17]，并在文献[21]中通过若干算例对含背景流影响的、以任意层速度[17]和以任意层伪速度[18]为特征速度的方程进行了较为详细的数值检验。以往通过规则波算例对Agnon型Boussinesq方程的数值检验[18,20-21]多以Stokes波或椭圆余弦波理论给定入射波边界条件，然而任何给定入射波边界与Boussinesq方程体系不符的情况均会导致计算过程产生高频寄生波[22]而影响数值检验效果，为此，本文以稳恒波的Fourier近似解[23]提供入射波边界，对以任意层速度为特征速度的Agnon型Boussinesq方程[17]开展了进一步的数值检验工作：首先，采用张洪生等[20]提出的同位网格有限差分格式，建立了以任意层速度为特征速度的Boussinesq方程数值计算模型；然后，通过均匀水深情况下深水和浅水域不同非线性水波传播变形的计算，检验了模型的色散性能和非线性性能；通过缓变和陡变斜坡地形上不同非线性水波的浅水变形计算，检验了模型的浅化性能及其关于陡坡地形的适用性；最后，给出了结论。

2 Boussinesq方程数值模拟模型

2.1 控制方程与计算格式

基于Agnon等[15]的思路，Wang等[17]以任意层水平和垂向速度为特征速度，推导了缓变地形上含背景水流影响的具有强非线性和频散性能的Boussinesq方程，无流情况下的空间一维方程体系可表达为：

(1)

(2)

(3)

(4)

(5)

(6)

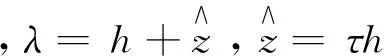
式(1)～(6)构成的偏微分方程组可采用同位网格有限差分法[20]进行数值求解。因为方程组包含了五阶空间导数项，为确保低阶导数项离散的误差阶数高于高阶导数项，所以对方程组中的空间导数项统一采用七点有限差分格式进行离散；同时，为保证时间导数项的计算误差不混淆方程组中的五阶空间导数，时间层上采用具有五阶精度的变步长Runge-Kutta-England格式向前步进。此外，需要说明的是，以空间七点有限差分格式离散偏微分方程组(3)～(6)将形成一个稀疏系数矩阵方程组，为降低矩阵方程的求解难度，采用变量重新排序的方法[20]，将稀疏系数矩阵方程组变换为带宽为27的带状矩阵方程组，并以列选主元的高斯消去法进行矩阵方程求解。

2.2 边界条件和数值滤波

2.2.1 入射波边界条件

内部造波源函数法[24—25]是Boussinesq方程数值模型入射边界条件常用的处理方法，该法在计算域内部指定位置处产生目标波，造波的准确性取决于造波源函数的合理解析。入射边界条件亦可给定，如采用Stokes波理论或椭圆余弦波理论给定[18,20—21]。较造波源函数法，依据波浪理论解析解给定入射波边界不仅可降低边界误差，而且可以考察Boussinesq方程与已有波浪理论的符合性，这是因为任何根据解析解给定的边界与Boussinesq方程体系不符的情况均会导致数值计算过程中产生高频寄生波[22]。考虑到式(1)～(6)构成的Boussinesq方程适用于深水至浅水的强非线性情况，所以本文采用稳恒波Fourier近似理论[23]给定入射波边界条件，这是因为较Stokes波和椭圆余弦波理论，Fourier近似理论关于深水至浅水波强非线性水波的解析具有更高的精度。此外，为了避免给定边界处的初始不稳定对数值计算的影响，我们对根据Fourier近似理论给定的入射波边界值G乘以一随时间变化的缓冲函数：

GR=Gtanh(t/NT)，

(7)

式中，N是常数，计算时取为5。

2.2.2 出流边界条件

出流边界条件的处理采用海绵层消波结合Sommerfeld辐射边界条件的方式进行。

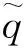
(8)

式中，d为海绵层网格节点至边界的距离；ds为海绵层宽度，当取为1～2倍波长的长度时即可获得较好的消波效果；α是海绵层缓冲参数，计算时取为3.5。

在一维情况下，Sommerfeld辐射边界条件表达为：

(9)

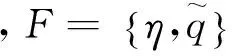
2.2.3 数值滤波

在以同位网格有限差分格式求解偏微分方程组时，因中心差分格式的奇偶失联，数值计算过程中会产生高频的格点振荡，数值实验显示：这些高频数值波动的振幅有随水深和非线性的增强而逐渐增强的趋势。为消除这种数值高频波对数值计算的影响，本文采用Bogey和Christophe[27]给出的具有低频散性和低耗散性的九点选择性滤波器进行滤除，如下：

(10)

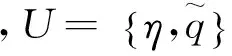
3 数值模型检验

3.1 均匀水深水域波浪传播的数值计算与检验

设置长度为20个波长、绝对水深h=1.4 m的均匀水深水槽。水槽左端为入射波边界，右端为开边界，并在开边界前设置长度为100dx(dx为空间步长)的海绵层进行消波。通过多种计算组合，对深水至浅水域的不同非线性水波的传播变形进行数值计算，具体的计算组合见表1，表中：H和T分别为波高和波周期，L是根据稳恒波Fourier近似理论计算得到的波长；算例包括深水波(h/L=1.0)和浅水波(h/L=0.05)两种情况，对于深水波，非线性参数波陡(H/L)最大为0.08；对于浅水波，非线性参数波高水深比(H/h)最大为0.6。各种情况下的计算参数(包括空间步长dx和时间步长dt)如表1所列；为确保得到稳定的计算结果，每种情况的计算总时间均取为50T。

图1a～d和图2a～d分别给出了深水域(h/L=1.0)和浅水域(h/L=0.05)中不同非线性水波在不同时刻(t=49.25T、49.50T、49.75T和50T)时无量纲波面(2η/H)的计算结果，图中亦给出了稳恒波Fourier近似解[23]的结果，为较为清晰地比较，图件仅对14L～16L这一区域进行了展示。结果显示：数值计算的波形规则，波动稳定，随着非线性的增强，波面不再关于静水面对称，波峰变得尖陡，波谷变得平坦。比较数值计算结果和Fourier近似解可知：对于深水和浅水域中的线性和弱非线性波(图1a，b和图2a，b)二者吻合良好，尤其是对于线性波的情况(图1a和图2a)，即使是对水深波长比为1.0的深水波，二者也几乎完全一致，说明模型具有优良的色散性能。随着非线性的增强，数值解与Fourier近似解的差异逐渐明显：一方面表现为数值解的振幅较Fourier近似解逐渐减小，这应该与数值计算的空间网格分辨率难以解析强非线性水波中的高频约束波有关；另一方面表现为数值解的位相较Fourier近似解逐渐超前，说明对于强非线性的情况数值模型存在夸大波速的现象。图3a，b分别给出了深水和浅水域中波速(c)和x=15L处波峰高度(ηc)的计算误差(Error)随入射波陡(H/L)和入射波波高水深比(H/d)的变化(误差定义为Error=(f1-f2)/f2×100：f={c,ηc}；下标1、2分别代表模型计算值和Fourier近似解；波速和波峰高度的计算值系通过上跨零点法据x≤15L范围内的数值波面统计得到)，误差分析显示：对于深水和浅水域中的强非线性水波，数值模型的波速误差分别为0.21%和0.78%，在传播15L后，波峰高度的误差也仅为-3.2%和-3.7%。

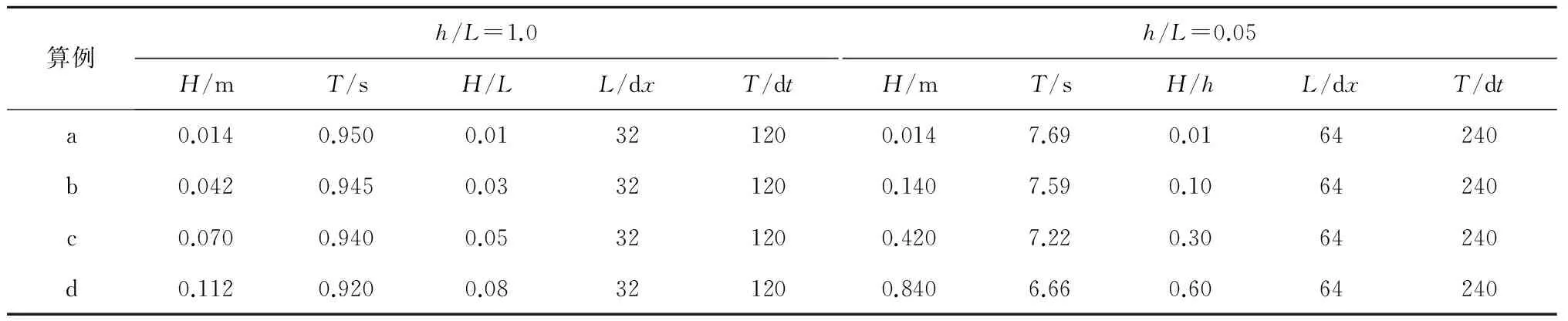
表1 均匀水深水域波浪传播变形实验算例

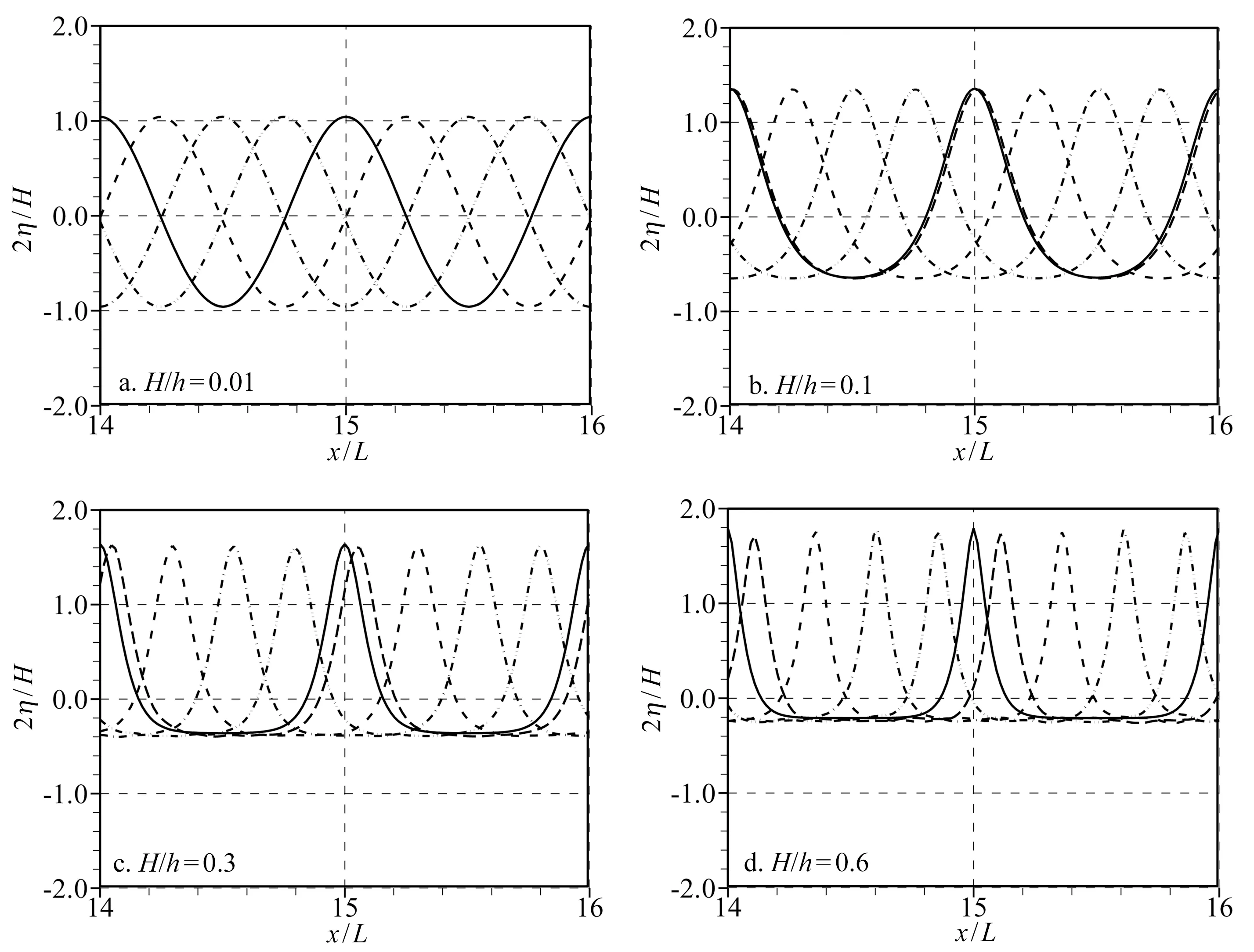
图2 浅水域(h/L=0.05)、不同非线性(H/h=0.01～0.6)水波、不同时刻(t=49.25T(虚线)、49.50T(点划线)、49.75T(双点划线)和50T(长虚线))的无量纲自由面(2η/H)计算结果(虚线)及与Fourier近似解(t=50T，实线)的比较Fig.2 Computed non-dimensional free surface displacement (2η/H) at t=49.25T (dash), 49.50T (dash-dot), 49.75T(dash-dot-dot) and 50T (long-dash) from the simulations of wave propagation in constant shallow depth (d/L=0.05). Solutions of Fourier approxima-tion method at t=50T are drawn as the solid lines in a-d

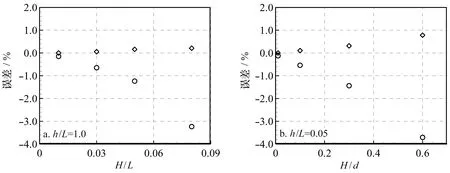
图3 深水域(a)和浅水域(b)中波速(◇)和波峰高度(○)的计算值较Fourier近似解的误差Fig.3 Relative errors between the computed results and the Fourier approximated solutions in constant deep depth (a) and shallow depth (b)

3.2 缓坡地形上波浪传播的数值计算：与解析解和解析数值解的比较

为了检验模型的浅水变形性能，对不同非线性水波自深水至浅水域的浅水变形过程进行了数值计算。图4给出了数值实验的计算范围及地形示意：数值水槽长为120 m，在x=0 m处设置坡度为1∶100的缓变斜坡，斜坡上部接平台；缓坡前平底段长度设置为14 m，水深(h0)为1.0 m；为保证数值计算过程不致因水深变浅诱导的波浪破碎而发散，平台水深(he)因入射波高的不同而有所变化(表2)。水槽右端设置为辐射边界，并在辐射边界前布置长度为100dx的海绵层进行消波；左端为给定的入射波边界: 波周期T0为1.13 s，对应的水深波长比h0/L0=0.5(L0=gT2/2π是根据线性波理论计算的深水波长)；波高(H0)在0.000 02～0.08 m(表2算例a～d)，对应的入射波陡H0/L0=0.000 01～0.04；其中算例a用于评价模型关于线性波浅水变形的计算效果，算例b～d用于考察模型关于有限振幅波浅水变形的计算效果。数值计算的空间步长dx和时间步长dt的取值分别如表2所列，各种情况下的计算总时间均为150T0，以最后5T0时间内的波面计算结果通过上跨零点法计算波高。

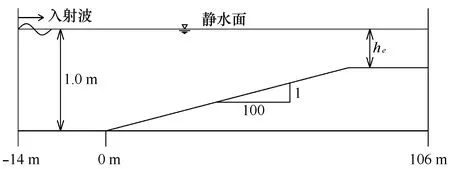
图4 缓坡地形上波浪传播变形数值实验地形示意Fig.4 Bottom profile for wave propagation on mild slope topography

表2 缓坡地形上波浪传播变形的实验算例

Tab.2 Cases for the computation of wave propagation on mild-slope topography

算例H0/mT0/she/mH0/L0dx/mT0/dta0.000021.130.040.000010.040150b0.021.130.040.010.024150c0.041.130.070.020.030150d0.081.130.120.040.030150

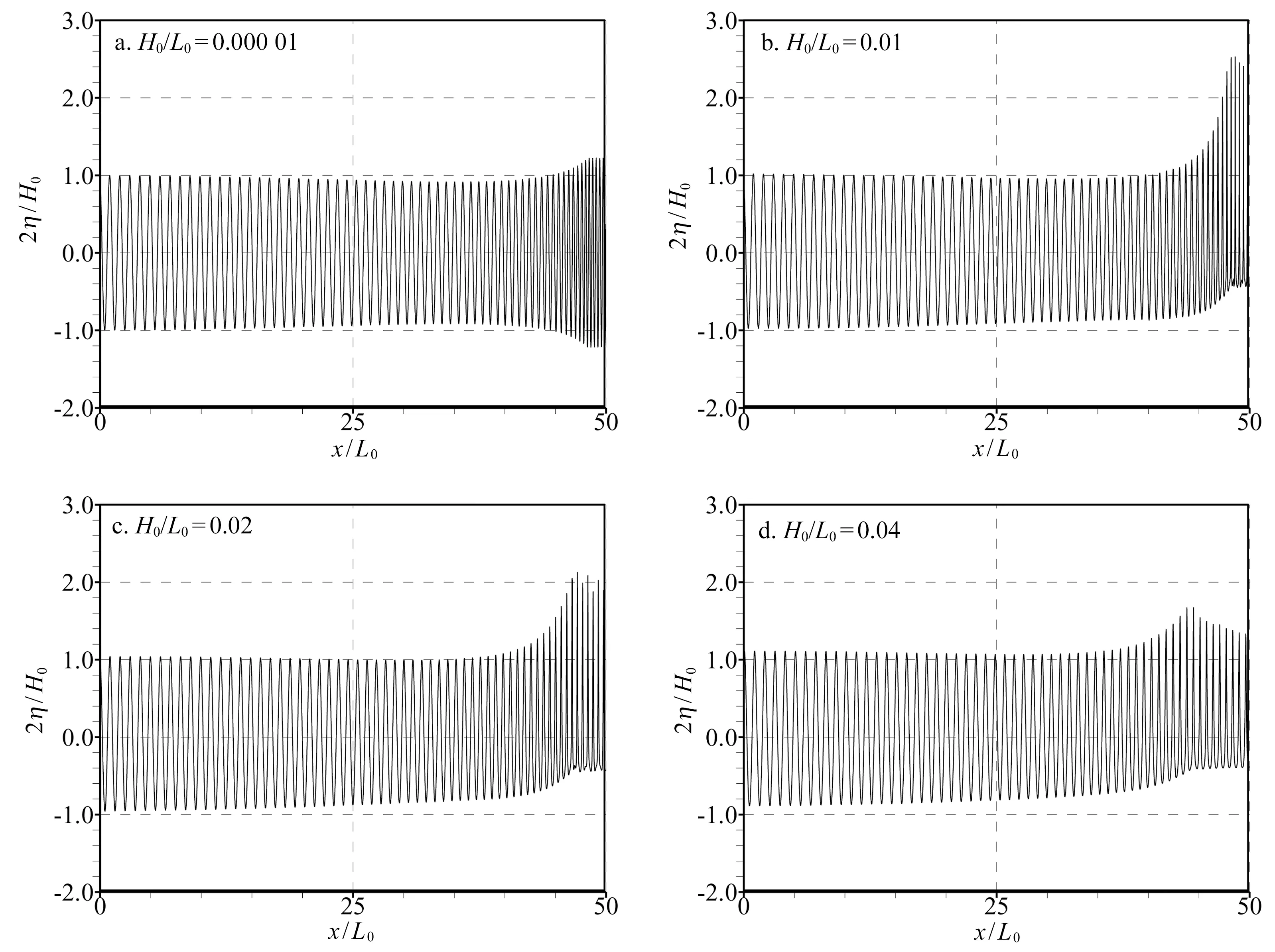
图5 不同入射波陡情况下无量纲波面(2η/H0)的浅水变形过程Fig.5 Profiles of the non-dimensional free surface displacement (2η/H0) during the shoaling process under different incident wave steepness

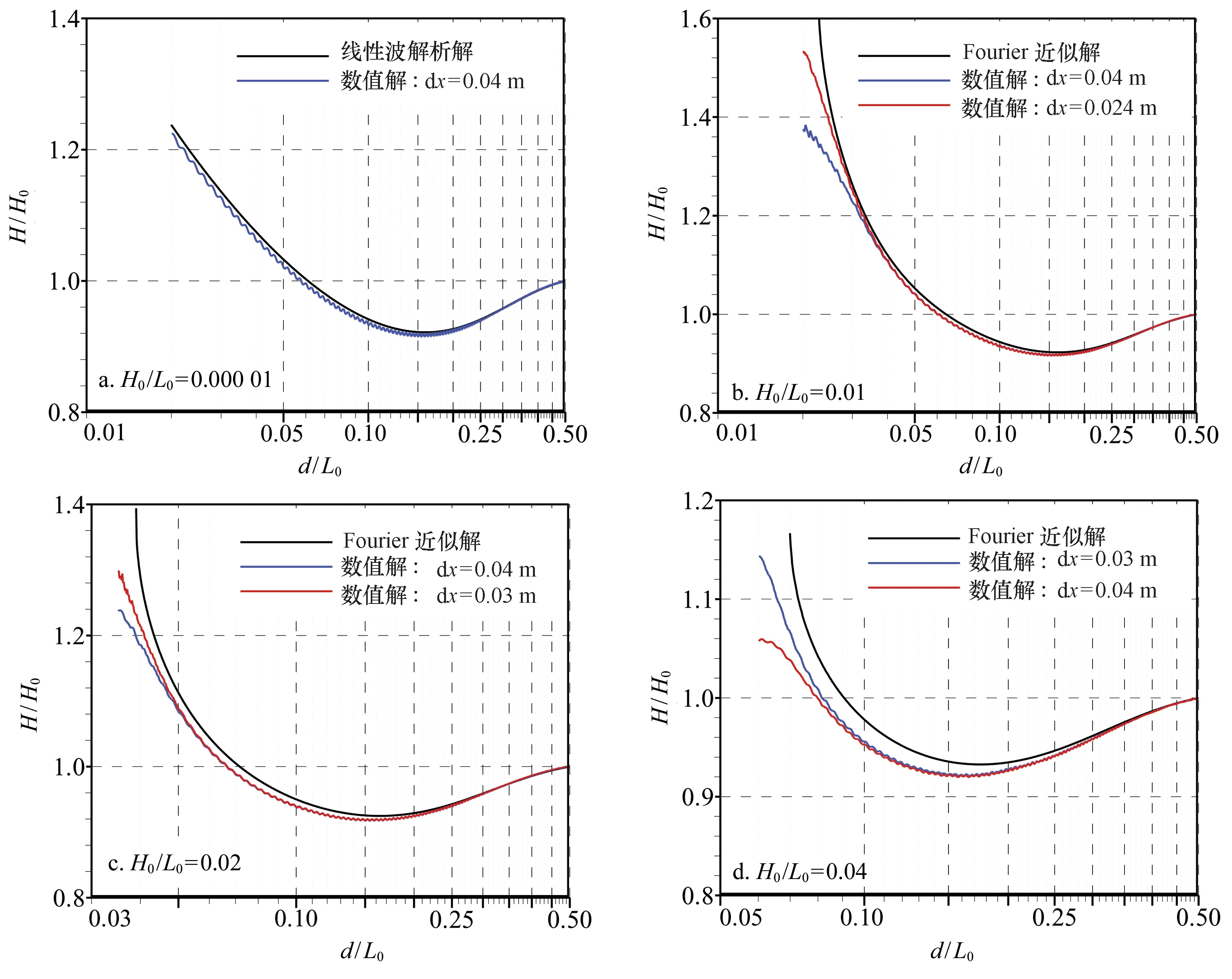
图6 不同入射波陡情况下无量纲波高(H/H0)的数值计算结果及其与解析解和解析数值解的比较Fig.6 Variations of the computational non-dimensional wave height (H/H0) and comparisons with those of linear theory and Fourier approximations during the shoaling process under different incident wave steepness

图7 Ting和Kirby[29](a)、以及Tsai等[30](b)的物理模型实验断面示意Fig.7 Experimental bottom profiles conducted by Ting and Kirby[29](a) and Tsai et al.[30](b)

图5a～d分别给出了t=150T0时刻时不同入射波陡(H0/L0=0.000 01～0.04)情况下无量纲波面(2η/H0)的沿程变化，由此可见：规则波在缓坡地形上传播时的波形规则，波态稳定；对于微幅入射波(图5a)的情况，数值波面关于静水位对称，且随着水深变浅，行进波的振幅呈先减小后增大的变化；对于有限振幅波的情况(图5b，c)，随着水深的减小，行进波的非线性作用渐强，表现为数值波面逐渐抬高，峰谷关于静水位不再对称，尤以斜坡末端平台起始位置处波面的波峰最为尖陡，波谷最为平坦，这是非线性作用生成高频谐波的表现。在平台初始位置处，算例b～d的局地波高水深分别为0.78、0.71和0.76，已接近或略小于孤立波一阶近似理论确定的浅水极限波高水深比0.78；自此之后，平台上的行进波有随传播距离的增大而渐小的趋势(图5b～d)。

图6a～d对不同入射波陡情况下无量纲波高(H/H0)的计算结果分别与解析解和解析数值解进行了比较，其中，微幅入射波(H0/L0=0.000 01)的计算结果与基于线性波理论的浅水变形解析解比较(图6a)；有限振幅入射波(H0/L0=0.01～0.04)的计算结果与基于稳恒波傅里叶近似理论的解析数值解[28]比较(图6b～d)。由此可知：在微幅入射波情况下(图6a)，数值结果与线性理论解析解吻合甚好，虽然计算格式的数值耗散使计算值有随传播距离的增加(水深的减小)而逐渐小于解析解的趋势，但二者的最大误差(坡顶处)仅为-0.97%；在有限振幅入射波情况下(图6b～d)，数值结果与解析数值解的差异亦随水深的减小逐渐增大，尤以近坡顶处的差异为最大，并且这一差异有随入射波陡的增加而逐渐增大的趋势，如：在d/L0=0.1时，算例b、c和d浅水变形系数计算值较解析数值解的误差分别为-0.83%、-1.17%和-2.26%；在d/L0分别为0.025、0.04和0.07时，算例b、c和d的计算值较解析数值解的误差分别为-2.45%、-5.77%和-8.62%。

有限振幅入射波情况下浅水变形系数计算值较解析数值解偏小的原因可能在于如下3个方面：一是数值滤波，它可能会滤除非线性作用产生的高频谐波而造成计算值偏小；其二源于微分方程差分近似产生的数值耗散，这一耗散与空间网格分辨率有关，一般情况下高的空间分辨率会产生小的数值耗散；其三可能是Boussinesq方程非线性浅化性能的限制所致，因为毕竟方程式(3)中用于控制浅水变形性能的系数b1和b3是通过线性化的Boussinesq方程与线性波浅水变形解析解的比较确定的[17]，本节微幅波浅水变形计算结果与解析解相符合(图6a)也辅证了线性理论情况下b1和b3系数的合理性。在数值滤波方面，本文采用了具有低频散性和低耗散性的九点选择性滤波器，根据Bogey和Bailly[27]的研究，此滤波器可有效滤除波长小于4.7dx的波动，这意味着对于非线性波的计算，如果在基频波长范围内设置47个空间网格步长，那么这样的空间分辨率可解析至10倍频约束谐波。因为数值耗散和数值滤波均与空间分辨率有关，所以为深入了解有限振幅情况下浅水变形计算值偏小的原因，我们对算例b～d分别在粗空间网格步长dx=0.04 m下开展了进一步的数值计算工作，并将相关计算结果示于图6b～d中。比较不同空间分辨率下的结果可知：(1)在水深波长比d/L0>0.08时(距入射波边界为49L0)，不同空间分辨率下的结果基本重合，这说明数值耗散不是造成计算结果偏小的原因，因为如果是数值耗散所致，那么在长距离传播后不同空间网格步长下的计算结果应略存差异；(2)随着水深波长比的进一步减小(d/L0<0.08)，不同空间分辨率下的计算差异逐渐明显，粗网格下的数值结果明显小于细网格，这是空间分辨率的不足造成非线性作用产生的高频约束谐波因数值滤波器的耗散作用所致，同样也是平台上行进波的振幅随传播距离逐渐减小的原因。因为在d/L0<0.08时不同入射波陡情况下的计算结果之于空间网格分辨率的敏感性甚小，所以有限振幅入射波浅水变形系数计算结果较解析数值解偏小的原因不是模型的数值耗散和数值滤波所引起，而应该是控制方程在非线性浅化性能方面的局限所致。

3.3 斜坡地形上波浪传播的数值计算：与物理模型实验的比较

以Ting和Kirby[29](记为TK)、以及Tsai等[30](记为Ts)进行的波浪水槽实验对模型在缓变和陡变斜坡上的浅水变形过程进行检验，图7给出了相应的实验情况：其中，TK实验断面是坡度为1/35的缓坡地形，Ts实验断面为斜坡平台地形，斜坡坡度包括1/10、1/5和1/3三种情况，平台高度为0.8 m。表3给出了模型实验的水深(h0)、入射波浪条件(H0、T0)、斜坡坡度(cotβ)、破碎位置(xb为相对于坡脚的水平距离)、破碎类型以及波浪数值模型计算的空间步长和时间步长，表中，Li是根据稳恒波Fourier近似理论计算得到的入射波波长，需要说明的是：Ts实验并未对破碎位置和破碎类型进行报道，表中给出的破碎位置是最大波高测波杆所在的位置(实际破碎位置可能产生于此位置前后)，破碎类型依据Galvin[31]的研究经由Irribarren数的判定得到。此外，因为现阶段的数值模型尚未包含任何破碎机制，所以为使计算过程不致因波浪破碎而发散，模型自破碎位置起至水槽末端设置100dx长度的海绵层。

图8a和8b分别给出了数值计算得到的TK两组实验的波面(η)沿程变化(零点起自坡脚)，为方便比较，该图亦将各测波杆记录的峰谷实验值示于其中。结果显示：数值计算得到的波形规则，波态稳定；因斜坡上水深的减小，行进波的浅水变形效应显著，峰谷关于静水面表现出强烈的不对称，尤以破碎位置处最为明显；在经过破碎位置后，行进波的振幅因海绵层的作用而逐渐减弱。比较破碎前波峰和波谷的数值计算结果和实验值可知，二者吻合良好，数值结果较好地反映了有限水深和浅水域中非线性水波浅水变形过程中的峰谷变化。

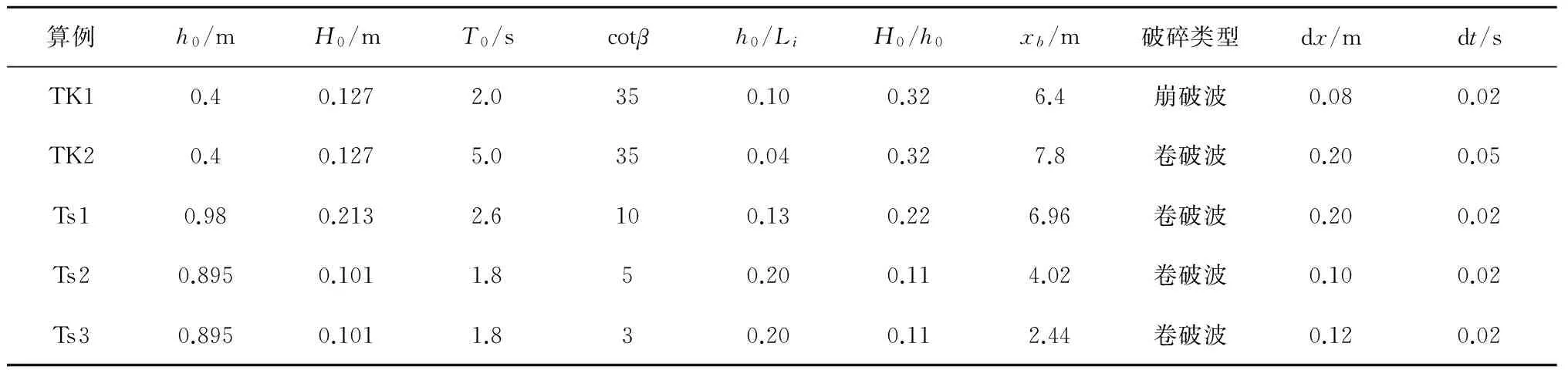
表3 斜坡地形上波浪传播变形的物理模型实验算例和数学模型计算参数

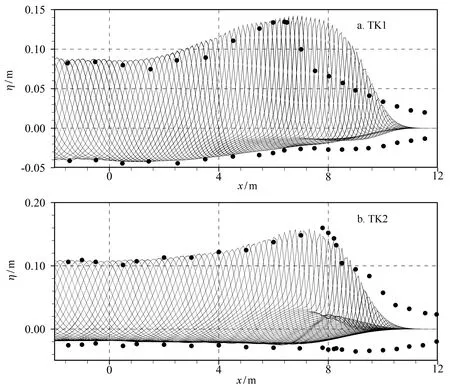
图8 波面(η)沿程变化计算值(实线)与实验值(实心圆点)的比较Fig.8 Variations of the computed free surface displacement (η) and comparisons with the experimental data

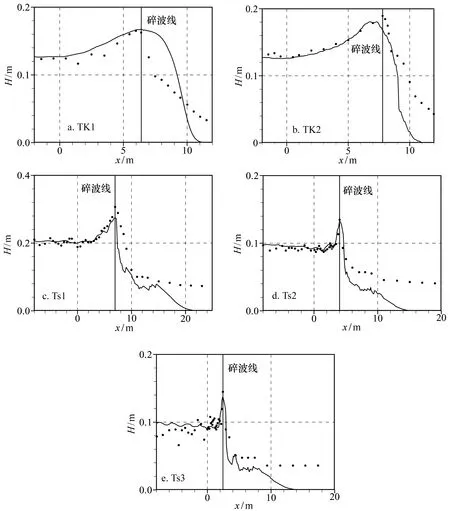
图9 波高(H)沿程变化的计算值(实线)与实验值(实心圆点)的比较Fig.9 Variations of the computed wave height (H) and comparisons with the experimental results

图9a～e分别给出了数值计算得到的TK和Ts 5组实验情况下波高的沿程变化，结果显示：对于缓坡(1/35)TK1和TK2实验，斜坡上的波高随水深的减小而缓慢增大；对于陡坡(1/10、1/5和1/3)Ts1、Ts2和Ts3实验，斜坡上的波高因水深的剧减而快速增强，斜坡前有一定程度的反射波生成，且反射波的振幅有随坡度的增大而逐渐增强的趋势。从最大波高的计算结果与实验值的比较可以看出：对于崩破波实验TK1，最大波高的发生位置和强度均与实验值吻合良好，且结合图8a可知，此时波峰和波谷值亦与实验值相吻合；对于卷破波TK2以及Ts1～Ts3实验，数值计算的最大波高值均略低于实验值，陡坡Ts1～Ts3实验中的最大波高位置与实验值相吻合，缓坡TK2实验中的最大波高位置较实验结果略为超前，这可能与Boussinesq方程无法描述卷波破碎时的波面翻卷现象有关。

4 结论

采用同位网格有限差分法，建立了强非线性和色散性Boussinesq方程数值计算模型。以稳恒波Fourier近似解提供入射波边界条件，对均匀水深深水和浅水域的行进波、以及缓变和陡变斜坡地形上不同非线性水波的浅水变形过程进行了数值计算，数值结果与解析解、解析数值解和波浪水槽实验值的比较表明：(1)模型具有良好的色散性能和非线性性能，至少可对深水(水深波长比1.0)强非线性(波高波长比0.08)以及浅水(水深波长比0.05)强非线性(波高水深比0.6)的行进波进行有效计算；(2)模型具有较好的浅水变形性能，可描述深水至浅水域弱非线性入射波的浅水变形过程；(3)尽管控制方程受限于缓变水深这一假设，但模型可对乃至1/3陡变斜坡上的浅水变形波进行较为合理地预测。

[1] Boussinesq J. Theory of wave and swells propagated in long horizontal rectangular canal and imparting to the liquid contained in this canal[J]. Journal de Mathematiques Pures et Appliquees, 1872, 17(2): 55-108.

[2] Peregrine D H. Long waves on a beach[J]. Journal of Fluid Mechanics, 1967, 27: 815-827.

[3] Witting J M. A unified Model for the evolution of nonlinear water waves[J]. Journal of Computational Physics, 1984, 56: 203-236.

[4] Madsen P A, Murray R, Sørensen O R. A new form of the Boussinesq equations with improved linear dispersion characteristics[J]. Coastal Engineering, 1991, 15(4): 371-388.

[5] Nwogu O. Alternative form of Boussinesq equations for nearshore wave propagation[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1993, 119(6): 618-638.

[6] Gobbi M F, Kirby J T. Wave evolution over submerged sills: test of a high-order Boussinesq model[J]. Coastal Engineering, 1999, 37(1): 57-96.

[7] Gobbi M F, Kirby J T, Wei G. A fully nonlinear Boussinesq model for surface waves.Part 2. Extension to O(kh)4[J]. Journal of Fluid Mechanics, 2000, 405: 181-210.

[8] Lynett P, Liu P L-F. Linear analysis of the multi-layer model[J]. Coastal Engineering, 2004, 51: 439-454.

[9] Lynett P, Liu P L-F. A two-layer approach to wave modeling[J]. Proceeding of the Rval Society A, 2004, 460: 2637-2669.

[10] Chazel F, Benoit M, Ern A, et al. A double-layer Boussinesq-type model for highly nonlinear and dispersive waves[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2009, 465: 2319-2346.

[11] Liu Z B, Fang K Z. Two-layer Boussinesq models for coastal water waves[J]. Wave Motion, 2015, 57: 88-111.

[12] Wei G, Kirby J T, Grilli S T, et al. A fully nonlinear Boussinesq model for surface waves. Part 1. Highly nonlinear unsteady waves[J]. Journal of Fluid Mechanics, 1995, 294: 71-92.

[13] Gobbi M F, Kirby J T, Wei G. A fully nonlinear Boussinesq model for surface waves, Part 2: Extension to O(kh)4[J]. Journal of Fluid Mechanics, 2000, 405: 18l-210.

[14] Zou Z L. A new form of higher order Boussinesq equations[J]. Ocean Engineering, 2000, 27(5): 557-575.

[15] Agnon Y, Madsen P A, Schäffer H A. A new approach to high-order Boussinesq model[J]. Journal of Fluid Mechanics, 1999, 399: 319-333.

[16] Madsen P A, Bingham H B, Liu H. A new Boussinesq method for fully nonlinear waves from shallow to deep water[J]. Journal of Fluid Mechanics, 2002, 462: 1-30.

[17] Wang Yalin, Zhang Hongsheng, Miao Guoping, et a1. A new approach to high order Boussinesq type equations with ambient currents[J]. China Ocean Engineering, 2005, 19(1): 49-60.

[18] Zhang Hongsheng, Wang Weiyuan, Feng Wenjing, et a1. A numerical model for nonlinear wave propagation on non-uniform current[J]. China Ocean Engineering, 2010, 24(1): 15-28.

[19] Fuhrman D R, Bingham H B. Numerical solutions of fully non-linear and highly dispersive Boussinesq equations in two horizontal dimensions[J]. International Journal of Numerical Methods in Fluids, 2004, 44(3): 231-225.

[20]张洪生, 冯文静, 王亚玲,等. 非线性波传播的新型数值模拟模型及其实验验证[J]. 海洋学报, 2007, 29(4): 137-147.

Zhang Hongsheng, Feng Wenjing, Wang Yaling, et al. A new approach to numerical simulation of nonlinear wave propagation and its experimental verification[J]. Haiyang Xuebao, 2007, 29(4): 137-147.

[21] Zhang Hongsheng, Wang Weijuan, Feng Wenjing, et al. Tests and applications of a Boussinesq model with ambient current[J]. Journal of Hydrodyanmics, 2010, 22(4): 526-536.

[22] McCabe M. Modelling nearshore waves, runup and overtopping[D]. Manchester: University of Manchester, 2011.

[23] Zhao Hongjun, Song Zhiyao, Li Ling, et al. On the Fourier approximation method for steady water waves[J]. Acta Oceanologca Sinica, 2014, 33(5): 37-47.

[24] Larsen J, Dancy H. Open boundaries in short wave simulations: a new approach[J]. Coastal Engineering, 1983, 7: 285-297.

[25] Schaffer H A, Sorensen O R. On the internal wave generation in Boussinesq and mild-slope equations[J]. Coastal Engineering, 2006, 53(4): 319-323.

[26] Fuhrman D R, Madsen P A, Bingham H B. Numerical simulation of lowest-order short-crested wave instabilities[J]. Journal of Fluid Mechanics, 2006, 563: 415-441.

[27] Bogey C, Christophe B. A family of low dispersive and low dissipative explicit schemes for flow and noise computations[J]. Journal of Computational Physics, 2004, 194(1): 194-214.

[28] Zhao H J, Kong J, Song Z Y. Shoaling of nonlinear surface water waves on depth uniform current[C]//Processing 35th Congress International Assoc Hydraul Research. Chengdu, 2013.

[29] Ting F C K, Kirby J T. Observation of undertow and turbulence in a laboratory surf zone[J]. Coastal Engineering, 1994, 24(1/2): 51-80.

[30] Tsai C P, Chen H B, Hwung H H, et al. Examination of empirical formulas for wave shoaling and breaking on steep slopes[J]. Ocean Engineering, 2005, 32(3/4): 469-483.

[31] Galvin C J. Breaker type classification on three laboratory beaches[J]. Journal of Geophysical Research, 1968, 73(12): 3651- 3659.

Numerical validation of a Boussinesq-type model for highly nonlinear and dispersive waves

Zhao Hongjun1, Jiao Yingxia1, Kong Jun1

(1.CollegeofHarbor,CoastalandOffshoreEngineering,HohaiUniversity,Nanjing210098,China)

In the present work a numerical highly nonlinear and dispersive Boussinesq-type model is developed based on a non-staggered finite difference technique. With the Fourier approximation method providing the incident wave boundary condition, the model is applied and verified against a set of three test cases for which analytical, numerical or experimental reference results are available: (1) propagation of linear and nonlinear periodic waves on deep and shallow depth, (2) shoaling of linear and nonlinear regular waves from deep to shallow water on a mild slope, and (3) transformation of regular waves on a mild slope and on steep slopes. Comparisons of the numerical results with the analytical, numerical and experimental ones confirm the capabilities of the model for the predictions of highly nonlinear and dispersive waves and for the computations of nonlinear wave shoaling on different slopes.

Boussinesq equation; nonlinearity; dispersion; shoaling

10.3969/j.issn.0253-4193.2017.05.002

2016-10-14；

2017-01-15。

江苏省自然科学基金青年基金项目 (BK20130827)；交通部重点科技项目(2015328521280)；水利部公益性科研专项(201501010)。

赵红军(1980—)，男，天津市蓟县人，博士，副教授，主要从事水波动力学理论与应用研究。E-mail:loyhg@hhu.edu.cn

P731.22

A

0253-4193(2017)05-0010-12

赵红军, 焦影霞, 孔俊. 强非线性和色散性Boussinesq方程数值模型检验[J]. 海洋学报, 2017, 39(5): 10-21,

Zhao Hongjun, Jiao Yingxia, Kong Jun. Numerical validation of a Boussinesq-type model for highly nonlinear and dispersive waves [J]. Haiyang Xuebao, 2017, 39(5): 10-21, doi：10.3969/j.issn.0253-4193.2017.05.002