基于一种改进A*算法的移动机器人路径规划

孙炜，吕云峰，唐宏伟,2†，薛敏

(1.湖南大学 电气与信息工程学院，湖南 长沙 410082；2.邵阳学院 电气工程系, 湖南 邵阳 422000)



基于一种改进A*算法的移动机器人路径规划

孙炜1，吕云峰1，唐宏伟1,2†，薛敏1

(1.湖南大学 电气与信息工程学院，湖南 长沙 410082；2.邵阳学院 电气工程系, 湖南 邵阳 422000)

针对全局路径规划问题提出了一种改进的A*算法.首先，采用栅格方法建立环境模型，使用A*算法进行初步的路径规划.其次，针对A*算法规划的路径冗余点较多以及路径长度和转折角度较大的缺陷，提出将A*算法规划出的路径按较小的分割步长进行分割，得到一系列路径节点.最后，从起点开始依次用直线连接终点，当直线没有穿过障碍物时，则将中间路径点剔除，减小路径长度和转折角度.在仿真实验和实物实验中，分析和比较了本文算法与A*算法以及另一种改进A*方法.另外还研究了在不同障碍率、任务点数量和分割步长的情况下，本文算法与其他算法的优劣.结果表明，本文算法能有效地减小路径长度和转折角度.

移动机器人；路径规划；A*算法；栅格法

路径规划问题一直是智能机器人领域的一个研究热点.移动机器人路径规划是指机器人基于机载传感器获得的环境信息规划出一条从起点到终点的无碰、安全的可行路径，并在此基础上尽可能地优化路径[1].移动机器人路径规划主要解决以下三个问题：第一是规划出的路径能使机器人从起点运动到终点；第二是采用相应的算法使得机器人能够避开环境中的障碍物；第三是在满足前面两点要求的基础上，尽可能地优化机器人的运动轨迹，通常是以规划出的路径最短作为优化目标[2].根据机器人对环境信息的感知程度，路径规划问题分为全局路径规划和局部路径规划.前者是指机器人在拥有全部环境信息的基础上进行的路径规划，又称为离线路径规划；后者是指机器人在只有部分环境信息的基础上进行的路径规划，又称为在线路径规划[3].本文主要讨论全局路径规划.

移动机器人路径规划的研究起始于20世纪70年代，到目前为止，已有大量的研究成果.针对全局路径规划，主要方法有可视图法、拓扑学法、人工智能算法和栅格法[4].文献[5]针对自由空间法当环境发生变化时，需要重新建立网络连接模型，因而导致路径规划算法的环境适应性差和实时性不高的缺陷，提出了一种基于可视图的全局路径规划算法，该方法是直接在环境地图上进行路径规划，从而提高了算法的环境适应能力和实时性.神经网络作为人工智能中一种重要的算法也被应用到了移动机器人路径规划领域，如文献[6]，首先建立了一个障碍物罚函数的神经网络模型，并得到了整条路径的能量函数；然后求得该函数的极小值点，且应用了模拟退火算法避免陷入局部最优；最终对得到的路径进行了优化，使得路径更加平滑和安全.除此之外，学者们还采用其它的智能算法来解决移动机器人路径规划问题，如模糊逻辑[7-9]，蚁群算法[10]，粒子群优化[11]，遗传算法[12-13]等.

栅格法是将机器人运动环境建立成一系列具有二值信息的网格模型，再用搜索算法获取最优路径.文献[14]提出了一种改进的A*算法，解决了传统A*算法得到的路径包含过多冗余点问题，并得到机器人在拐点处的最小转折角度.但该算法并没有减小机器人的路径长度和转折角度.文献[15]针对传统A*算法得到的路径折线多、累计转折角度大的问题，提出了一种平滑A*算法，减少了不必要的路径点并减小了路径长度和转折角度.但只是在原有的路径点上进行处理，路径长度和转折角度的减少量有限.本文提出了另一种改进的A*算法，将进一步地减少移动机器人的总路径长度和总转折角度.

1 环境模型描述

众所周知，移动机器人工作环境地图建立是路径规划中十分重要的一步.地图建立是指将各种传感器获得的环境信息进行融合并抽象成地图模型[16].采用栅格单位描述二维环境信息非常简单有效，应用广泛.所以，本文也使用栅格法来建立移动机器人工作环境模型.如图1所示，栅格法将机器人工作环境分割成一系列具有相同尺寸的栅格，并将这些栅格分成两类：可通过栅格和不可通过栅格.图1中，空白栅格表示可通过栅格，即移动机器人能自由通过的地方，黑色栅格表示不可通过栅格，即该栅格有静态的障碍物.

为了方便研究又不失一般性，本文做出以下3点合理的假设：1)障碍物边界是在实际边界的基础上加一个移动机器人安全距离得到的，这样就可以将移动机器人看作是环境中的一个质点；2)在这有限的二维空间中，机器人的移动方向可以是任意的，并且不考虑高度的影响；3)在整个路径规划过程中，环境信息是不变的.图1是一个10*10的移动机器人工作环境，S是机器人起点，D是终点.本文的工作就是找到一条从起点到终点的无碰的最优路径.

图1 移动机器人工作环境

2 A*全局路径规划算法

A*算法是一种典型的启发式搜索方法.通过估价函数来引导和决定它的搜索方向.从起点开始搜索周围的节点，由估价函数得到每个节点的价值，选择价值最低的作为下一个扩展节点，循环重复这一过程直到搜索到终点，则停止搜索，获得最终路径.由于每一次都是以估价值最低的节点作为扩展节点，所以最终的路径代价是最低的.估价函数由式(1)给出：

f(n)=g(n)+h(n)

(1)

式中:g(n)是状态空间中从起始节点到节点n的实际代价，h(n)是从节点n到终点的启发式估计代价函数，本文采用曼哈顿距离作为启发式函数[14].

h(n)=|xd-xn|+|yd-yn|

(2)

xd是目标点的横坐标，yd是目标点的纵坐标，xn是节点n的横坐标，yn是节点n的纵坐标.

在A*算法搜索路径的过程中，需要不断地更新两个列表，一个是开启列表，另一个是关闭列表.开启列表存储的是所有的周围节点.A*算法从开启列表中选择具有最小估价值的节点作为下一个扩展节点.关闭列表存储的是所有经过的节点和环境中的障碍节点.应用A*算法进行路径搜索的具体流程如下所述：

Step1 把起始节点放入开启列表.

Step2 检查开启列表是否为空，如果为空，则表示搜索失败；不为空，则执行Step3.

Step3 选取开启列表中具有最低f(·)的节点作为当前扩展节点，对扩展节点的每个周围节点作如下处理：①当该节点的周围节点是障碍点或者是关闭列表中的节点，则没有任何动作；②当该节点的周围点不在开启列表中，则把该节点的周围节点添加进开启列表中，并将当前扩展节点作为该节点的周围节点的父节点，计算该节点的周围节点的f(·)和g(·)；③当该节点的周围节点在开启列表中，如果以当前扩展节点作为父节点，该节点的周围节点的g(·)比原来更低，则把当前扩展节点作为父节点，并重新计算该节点的周围节点的f(·)和g(·)．否则，不作任何改变.

Step4 将当前扩展节点放入关闭列表中，并检查终点是否在开启列表中.如果不在开启列表中，则跳回Step2继续搜索；否则，最优路径已经找到，结束搜索.

Step5 从终点开始，沿着每一个父节点移动，回到起始点，这就是最终的路径.

3 改进的A*算法

采用A*算法进行移动机器人路径规划虽然能获得一条安全无碰的路径，但路径点较多，折线多，导致路径的总长度和总转折角度较大.这在移动机器人实际应用中将消耗更多的能量和花费更多的时间.本文提出了一种改进的A*算法，能有效地减少路径长度和转折角度.

图2的实线是在一个任意环境中A*算法规划出的路径，本文方法是在原路径的基础上，从起点开始以较小的步长分割原路径，得到更多路径点，如图2的路径点a1到a20.按照一定的规则剔除冗余路径点，将剩余的路径点按顺序连接，最终获得更加优化的路径.

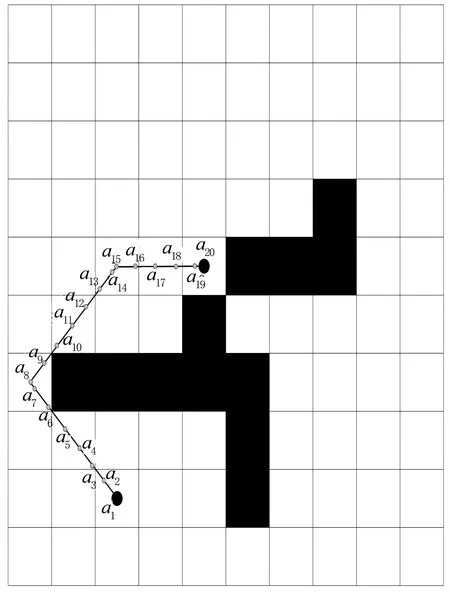
图2 A*算法规划的路径

图3是本文算法的流程图，图中符号的定义如下：

k为分割路径的步长；c,m,i分别是当前路径点下标、待连接路径点下标和新路径点下标；A为以步长k分割原始路径得到的路径点集合A={a1,a2,…,aN}，其中a1是起始点，aN是终点；ac为当前路径点；am为当前待连接点；lcm为连接ac与am的直线；lc,c+1为连接ac与ac+1的直线；B为新的路径点集合，B={b1,b2,…,bs}.

注意，以步长k分割路径是在原路径的直线段进行的.例如，对图4中A*算法得到的路径进行分割，先进行直线段L1的分割，从起点开始依次得到路径点a1,a2,…,a7，此时a8与原路径点的距离小于步长k，则将原路径点作为a8，并从路径点a8开始重复上述过程，分割直线段L2和L3直到将终点作为路径点a20时，分割过程结束.

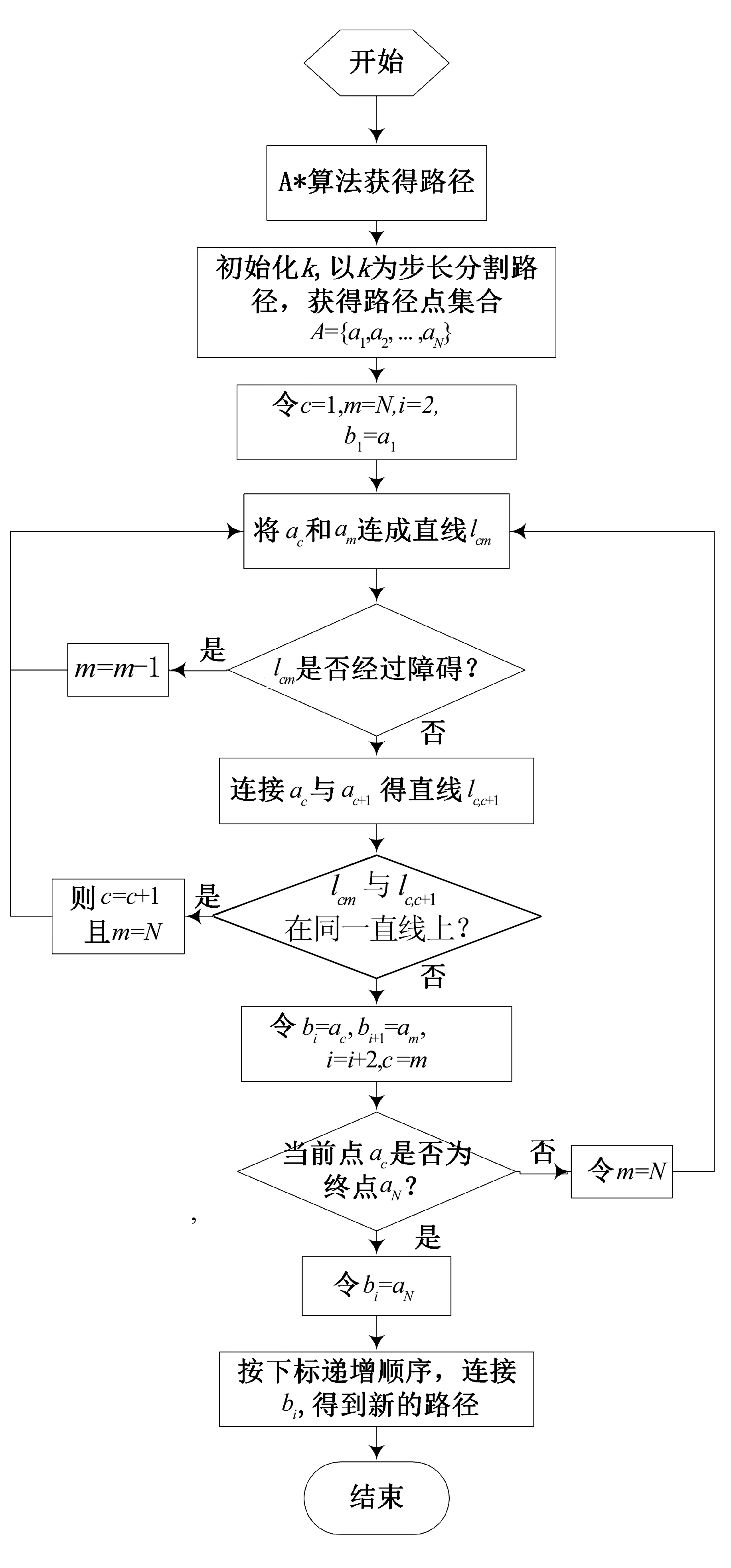
图3 改进A*算法移动机器人路径规划流程图

图4中的实线是在任意环境中A*算法规划出的路径1，由直线段L1,L2和L3组成，本文方法规划出的路径3由直线段La1a6,La6a9,La9a10和La10a20组成，其中Laiaj是指起点为ai，终点为aj的直线段.由图4可以直观地看出：路径1的路径长度明显大于路径3的路径长度.另外，路径1的总转折角度：

θ1=α1+β1

(3)

其中α1=∠ba8a9,β1=∠ca15a20．

路径3的总转折角度：

θ3=α2+β2+γ1

(4)

其中α2=∠ba6a9,β2=∠da9a10,γ1=∠ca10a20．而α1=α2+β2,β1=γ1+γ2,γ2=∠a15a20a10,则θ1=α1+β1=α2+β2+γ1+γ2=θ3+γ2．所以，θ1>θ3.相对于A*算法，本文方法缩短了总路径长度，减小了总转折角度.

文献[15]提出的平滑A*算法直接地剔除A*算法规划出的路径点，使得路径更加平滑.而本文方法是先进行分割，再剔除冗余的路径点.图4中直线段La1a8,La8a11和La11a20是文献[15]中平滑A*算法得到的路径2.显然，路径2的长度大于路径3的长度.另外，路径2的转折角度：

θ2=α1+β3

(5)

其中α1=∠ba8a9,β3=∠a15a20a10,而α1=α2+β2,β3=γ1+γ3,γ3=∠a11a20a10,则θ2=α1+β3=α2+β2+γ1+γ3=θ3+γ3,所以θ2>θ3.相对于文献[15]提出的平滑A*算法，本文方法得到的路径也更加优化.

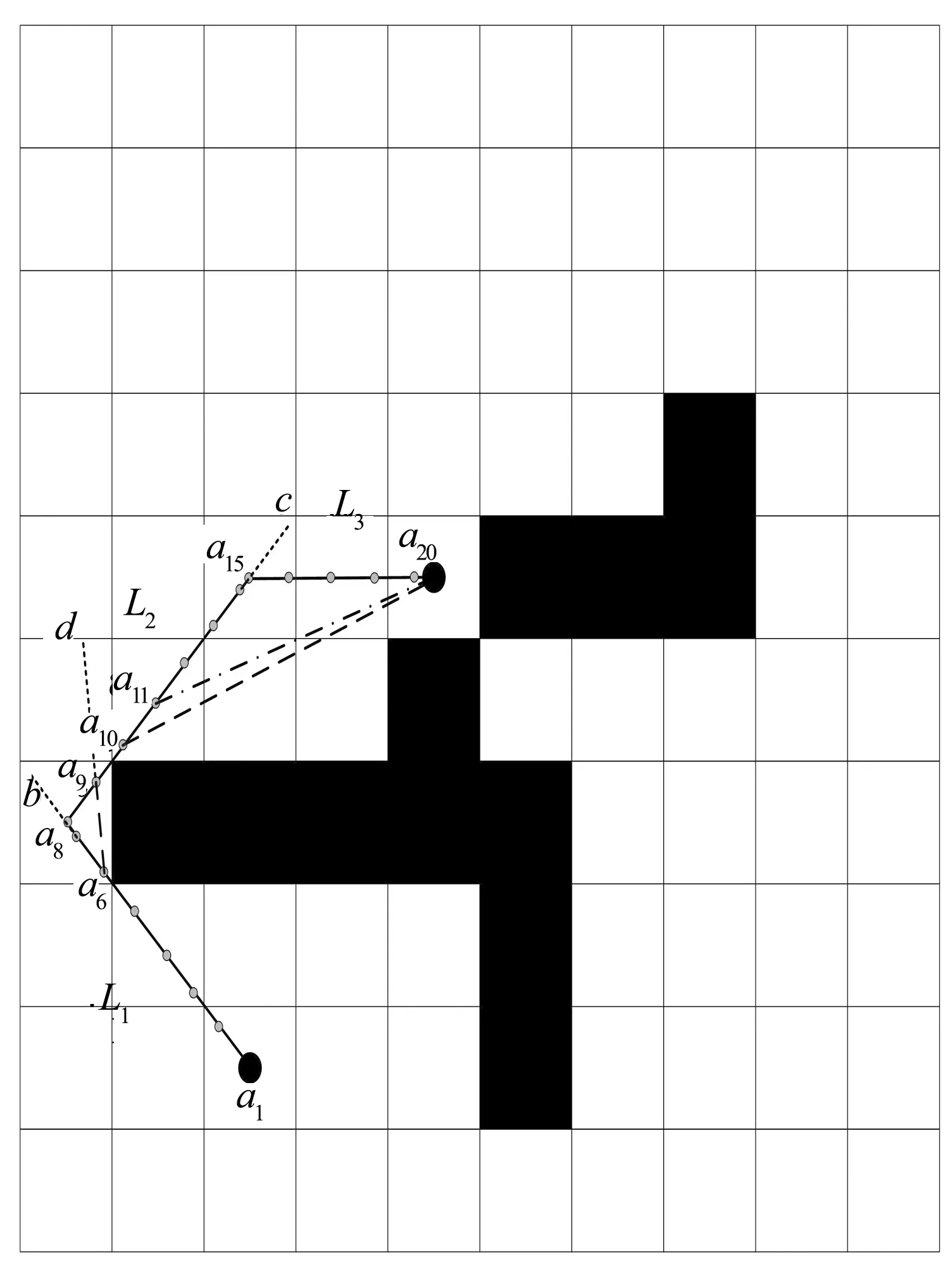
图4 A*算法、文献[15]平滑A*算法和本文改进A*算法规划的路径

4 实 验

为了验证本文算法的可行性和有效性，进行了计算机仿真实验和实物实验.考察了不同情形下算法的性能，以下将从4个方面进行仿真实验: 1)探究同样的条件下本文算法与A*算法以及文献[15]的平滑A*算法的性能；2)环境障碍率p对各算法的影响；3)不同目标点数n下算法的优劣；4)本文算法在不同的分割步长k下的效果.以下的4种情形都是在边长为200个单位的正方形环境下进行实验，将实验环境分割成20*20个栅格元素，每个元素是边长为10个单位的正方形栅格.将实验环境分割成20*20个栅格元素，每个元素是边长为10个单位的正方形栅格.

情形1 环境障碍率(障碍栅格数量占总栅格数量的比例)p=30%，取本文算法的分割步长k=0.1，目标数n=1即只有一个终点，起点是(4，4)，终点是(198，198)，机器人在起点的角度为90°.进行了50次实验，图5和图6是不同算法规划出的路径长度和转折角度，表1是3种算法50次实验的各项平均值比较.从实验结果中可以看出，本文提出的改进A*算法相对于A* 算法和文献[15]的平滑A* 算法，有效地减少了路径长度和转折角度.注意，虽然环境障碍率都是30%，但障碍栅格是随机分布的，这就导致了不同的环境复杂度，所以同样的算法和实验条件在不同的实验次数下却有不同的实验结果.

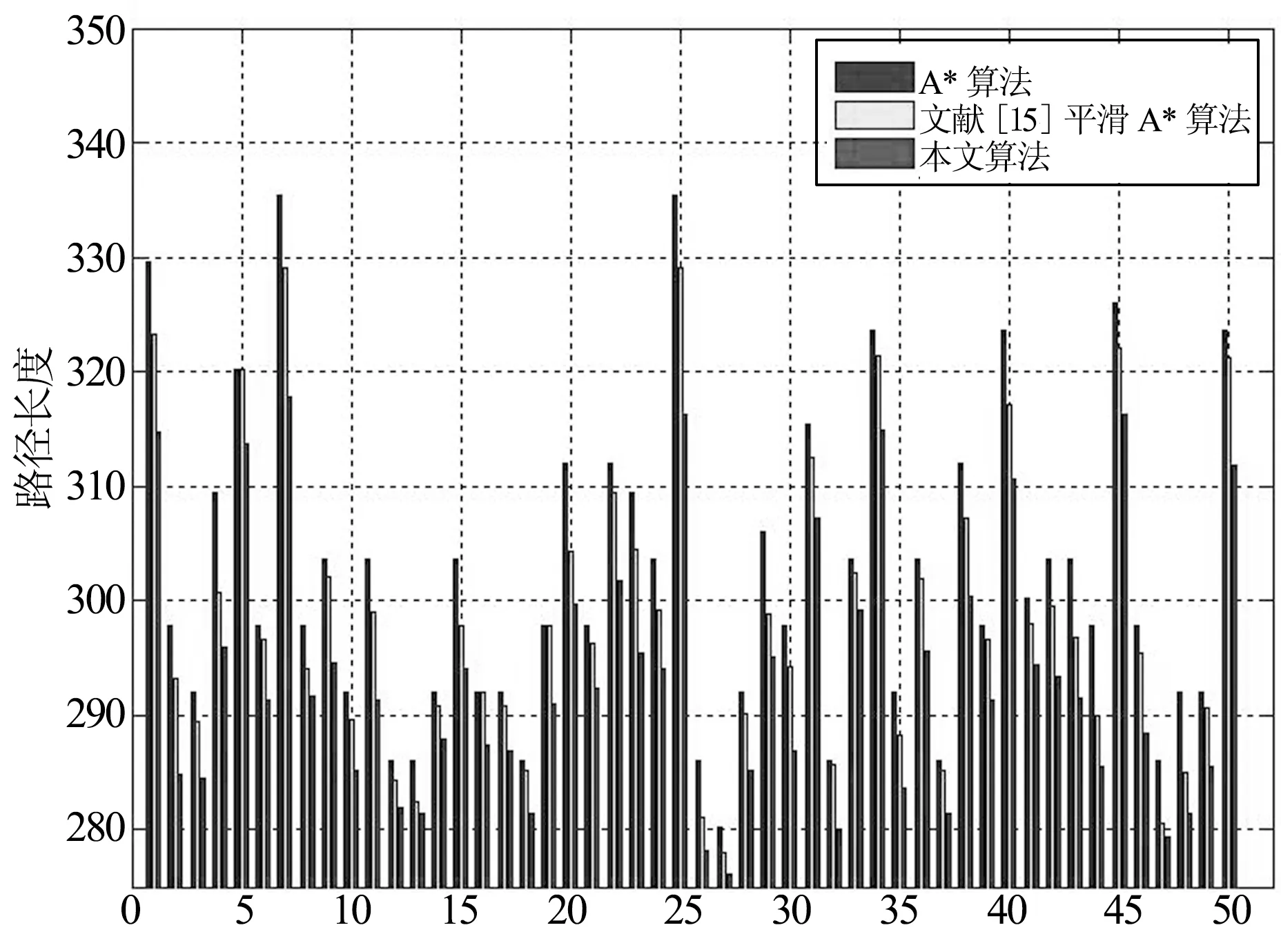
实验次数

实验次数

表1 A*算法、文献[15]平滑A*算法和本文算法的各项平均值

Tab.1 The mean values of A* algorithm、smoothing A* algorithm and proposed algorithm

性能指标A*算法文献[15]平滑A*算法本文方法平均路径长度302.2659298.8240293.3979平均转折角度518.4000384.3007268.8079相对A*算法路径长度减少率/%-1.142.93相对A*算法转折角度较少率/%-25.8748.15

情形2 考察在不同的环境障碍率下，各个算法的性能.令分割步长k=0.1，目标数n为1，起点(4，4)、终点(198，198)，机器人在起点的角度为90°.分别在环境障碍率为10%,20%,30%,40%,50%时，进行了50次实验，并求得不同障碍率下路径长度的均值和转折角度的均值，实验结果如图7、图8所示.可以看出，一方面当环境障碍率增大时，各个算法得到的路径长度和转折角度也在不断增大.这是因为环境障碍率一定程度上代表了环境的复杂度，当环境越复杂时，那么规划的路径长度和转折角度也就越大；另一方面，在图7和图8中，方框内的数据是本文算法相对于A*算法路径长度和转折角度的减少量.当环境障碍率越大时，路径长度和转折角度的减少量也不断增大，这说明相对于A*算法，本文方法更加适合在障碍物较多的环境中使用.

环境障碍率p

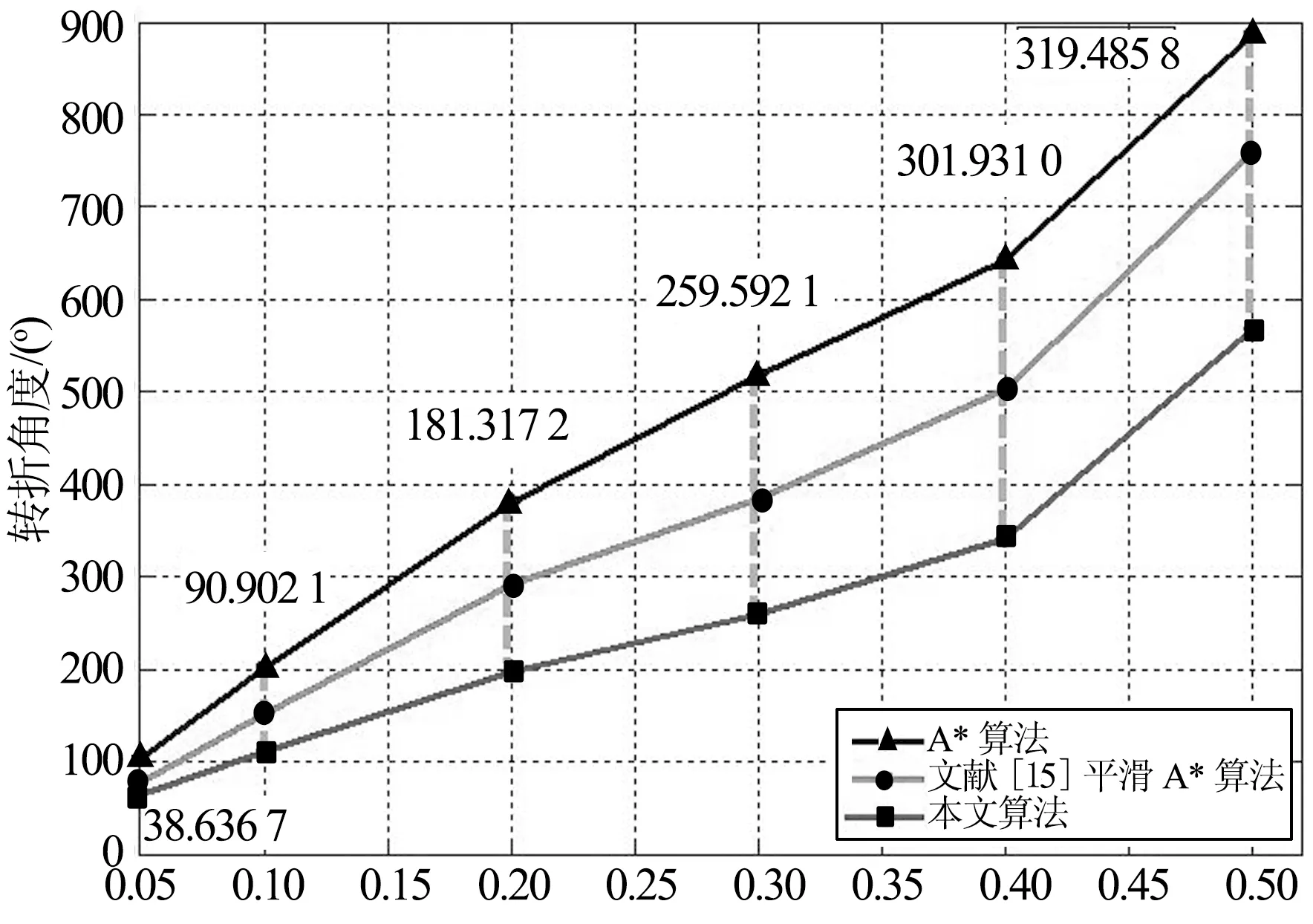
环境障碍率p

情形3 在移动机器人的工作空间中可能存在多个任务点，这就意味着环境中会有多个不同的终点.这里将研究当机器人有多个任务点时，各个路径规划算法的优劣性.这里做以下两点规定:1)对环境中的任务点进行了编号，任务点1,(198，198);任务点2,(4,198);任务点3,(95,95);任务点4,(198,4).2)当机器人有n个任务需要执行时，它的执行顺序是由任务点1递增至任务点n.取障碍率p=30%，分割步长k=0.1，分别在n等于1,2,3,4时，进行了50次实验，并求得路径长度和转折角度的均值，实验结果如图9和图10所示，图中方框内的数据是本文算法相对于A*算法路径长度和转折角度的减少量.显而易见，当机器人的任务点越多，本文算法相对于A*算法规划的路径长度和转折角度的减少量越大.

任务数

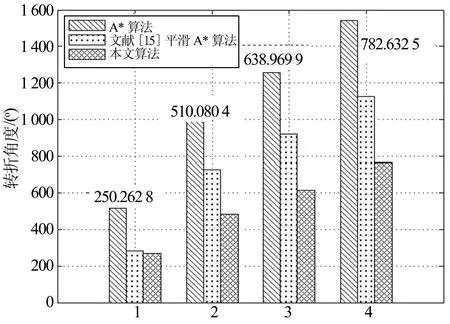
任务数

情形4 本文算法中存在一个分割步长k，这里将考察参数k对算法效果的影响.令环境障碍率p=30%，仅有一个任务点(198，198)，起点是(4,4)，机器人在起点的角度为90°.在不同的分割步长下进行了50实验，并求出相应的均值，实验结果如图11和图12所示.可以得出这样的结论：当分割步长越小时，本文算法得到的路径长度和转折角度也越小.显然，这是因为分割步长越小，路径分割得越精细，路径长度和转折角度也就相应减小.

步长k

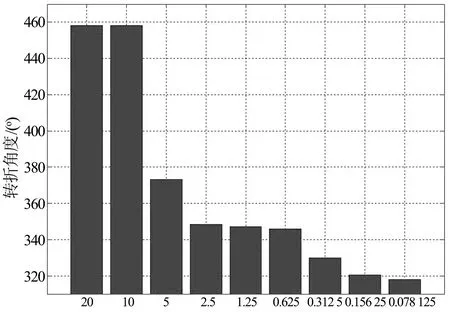
步长k

在实物实验中，本文采用的移动机器人是Turtlebot2，移动底座的最大移动速度：0.7 m/s，最大角速度：180°/s.采用ThinkPad E450C笔记本电脑作为移动机器人的控制器.移动机器人的实际运动空间如图13所示，是3.6 m×6.6 m的矩形环境.起点(0.9 m，0.9 m)，终点(2.7 m，6.3 m)，机器人在起点的角度为90°.为了使用本文改进的A*算法进行路径规划，需要先建立环境的栅格模型，设置栅格元素为0.6 m×0.6 m的正方形，对实际障碍物进行膨化处理，映射成图14的黑色栅格.分别采用A*算法、文献[15]的平滑A*算法和本文算法进行移动机器人的路径规划.图14的直线段La1a5,La5a11,La11a21,La21a27,La27a32,La32a44和La44a53是A*算法规划出的路径；文献[15]中平滑A*算法得到的路径是直线段La1a5,La5a11,La11a21,La21a27,La27a32和La32a53；直线段La1a8,La8a24,La24a25,La25a35和La35a53是本文算法得到的结果.由于移动机器人的运动总是存在外界干扰和运动精度等因素，其运动的实际路径长度与转折角度总是比规划的路径长度和转折角度要稍稍大一些，如表2所示.但无论是规划的路径长度和转折角度，还是移动机器人实际运动的路径长度和转折角度，本文算法得到的实验结果都比A*算法和文献[15]平滑A*算法更加优化.

图13 移动机器人的实际工作环境

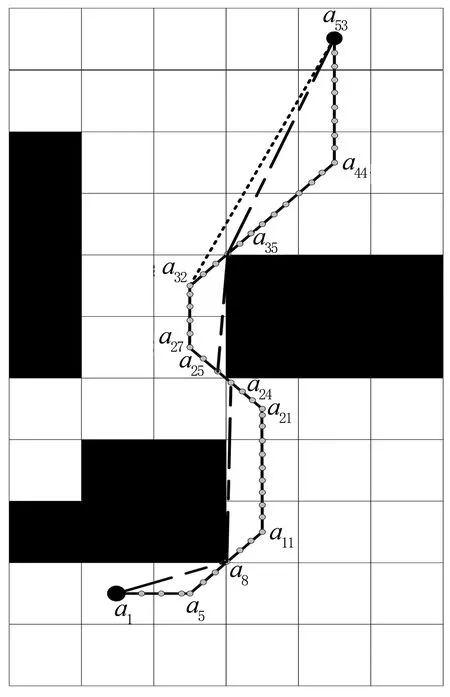
图14 移动机器人实际工作环境栅格模型和路径规划结果

表2 规划的和实际的路径长度，转折角度

Tab.2 The planning and the actual path lengths，turning angles

性能指标A*算法文献[15]平滑A*算法本文方法规划的路径长度/m6.9946.7806.473实际的运动路径长度/m7.26.96.6规划的转折角度/(°)360337.43330.72实际运动的转折角度/(°)377351346

5 结 论

采用A*算法进行移动机器人路径规划，可以得到一条从起点连接终点的无碰安全路径，但路径的冗余点较多，路径长度和转折角度较大.针对这些问题，本文提出了一种改进A*算法，能有效地减少路径冗余点和减小路径长度及转折角度.并且，分析比较了不同的环境障碍率、任务点数量、分割步长对算法性能的影响.一方面，相对于A*算法，本文方法更加适合多任务点，高障碍率环境下的移动机器人路径规划；另一方面，采用较小的分割步长可使得规划出的路径更加优化.

[1] 席裕庚,张纯刚.一类动态不确定环境下机器人的滚动路径规划[J].自动化学报,2002,28(2): 161-175.

XI Yugeng, ZHANG Chungang.Rolling path planning of mobile robot in a kind of dynamic uncertain environment[J]. Acta Automatica Sinica, 2002,28(2):161-175.(In Chinese)

[2] 张捍东,郑睿,岑豫皖.移动机器人路径规划技术的现状与展望[J].系统仿真学报,2005, 17(2): 439-443.

ZHANG Handong, ZHENG Rui, CEN Yuwan. Present situation and future development of mobile robot path planning technology[J]. Journal of System Simulation, 2005,17(2):439-443.(In Chinese)

[3] 朱大奇,颜明重.移动机器人路径规划技术综述[J].控制与决策,2010, 25(7): 961-967.

ZHU Daqi, YAN Mingzhong. Survey on technology of mobile robot path planning[J]. Control and Decision, 2010,25(7):961-967.(In Chinese)

[4] 吴乙万,黄智.基于动态虚拟障碍物的智能车辆局部路径规划方法[J].湖南大学学报:自然科学版,2013,40(1): 33-37.

WU Yiwan, HUANG Zhi. Dynamic virtual obstacle based local path planning for intelligent vehicle[J]. Journal of Hunan University:Natural Sciences, 2013,40(1):33-37.(In Chinese)

[5] 杨淮清,肖兴贵,姚栋.一种基于可视图法的机器人全局路径规划算法[J].沈阳工业大学学报,2009,31(2): 225-229.

YANG Huaiqing, XIAO Xinggui, YAO Dong. A V-graph based global path planning algorithm for mobile robot[J]. Journal of Shenyang University of Technology, 2009,31(2):225-229.(In Chinese)

[6] 梁瑾,宋科璞.神经网络在移动机器人路径规划中的应用[J].系统仿真学报,2010,22(增刊1): 269-272.

LIANG Jin, SONG Kepu. The application of neural network in mobile robot path planning[J]. Journal of System Simulation, 2010,22(s1):269-272.(In Chinese)

[7] 郝冬,刘斌.基于模糊逻辑行为融合路径规划方法[J].计算机工程与设计,2009,30(3): 660-663.

HAO Dong, LIU Bin. Behavior fusion path planning method for mobile robot based on fuzzy logic[J]. Computer Engineering and Design, 2010,30(3):660-663.(In Chinese)

[8] ARPINO C P, MELENDEZ W M, GUZMAN J,etal. Fuzzylogic based speed planning for autonomous navigationunder velocity field control[C]//2009 IEEE Int Conf on Mechatronics. Malaga, 2009: 201-212.

[9] ZOUMPONOS G T, ASPRAGATHOS N A. Fuzzy logic pathplanning for the robotic placement of fabrics on a worktable[J]. Robotics and Computer Integrated Manufacturing, 2008, 24 (2): 174-186．

[10]邓高峰,张雪萍,刘彦萍.一种障碍环境下机器人路径规划的蚁群粒子群算法[J].控制理论与应用,2009,26(8): 879-883.

DENG Gaofeng, ZHANG Xueping, LIU Yanping. Ant colony optimization and particle swarm optimization for robot-path planning in obstacle environment[J]. Control Theory & Applications, 2009,26(8):879-883.(In Chinese)

[11]吴宪祥,郭宝龙,王娟.基于粒子群三次样条优化的移动机器人路径规划算法[J].机器人,2009,31(6): 556-560.

WU Xianxiang, GUO Baolong, WANG Juan. Mobile robot path planning algorithm based on particle swarm optimization of cubic splines[J]. ROBOT, 2009,31(6):556-560.(In Chinese)

[12]王雪松,高阳,程玉虎,等.知识引导遗传算法实现机器人路径规划[J].控制与决策,2009,24(7): 1043-1049.

WANG Xuesong, GAO Yang, CHENG Yuhu,etal. Knowledge-guided genetic algorithm for path planning of robot[J]. Control and Decision, 2009,24(7):1043-1049.(In Chinese)

[13]THEODORE M, KAVEH A, ROGER L W. Genetic algorithms for autonomous robot navigation[J]. IEEE In Strumentation and Measurement Magazine, 2007,12(1): 26-31.

[14]王殿君.基于改进A*算法的室内移动机器人路径规划[J].清华大学学报:自然科学版,2012, 52(8): 1085-1089.

WANG Dianjun. Indoor mobile-robot path planning based on an improved A* algorithm[J]. Journal of Tsinghua University:Science and Technology,2012,52(8):1085-1089.(In Chinese)

[15]王红卫,马勇,谢勇,等.基于平滑A*算法的移动机器人路径规划[J].同济大学学报：自然科学版,2010,38(11): 1647-1651.

WANG Hongwei, MA Yong, XIE Yong,etal. Mobile robot optimal path planning based on smoothing A* algorithm[J]. Journal of Tongji University:Natural Science, 2010,38(11):1647-1651.(In Chinese)

[16]朱庆保,张玉兰.基于栅格法的机器人路径规划蚁群算法[J].机器人,2005,27(2): 132-136.

ZHU Qingbao, ZHANG Yulan. An ant colony algorithm based on grid method for mobile robot path planning[J]. ROBOT, 2005,27(2):132-136.(In Chinese)

Mobile Robot Path Planning Based on an Improved A* Algorithm

SUN Wei1, LV Yunfeng1, TANG Hongwei1,2†, XUE Min1

(1.College of Electrical and Information Engineering, Hunan University, Changsha 410082, China；2.Department of Electrical Engineering, Shaoyang University, Shaoyang 422000, China)

An improved A* algorithm was presented for global path planning of mobile robot. Firstly, the environment model was described using the grid method, and the preliminary path was obtained by traditional A* algorithm. Secondly, the path planned by A* method was flaw with much redundant points, large path length, and turning angle. The original path was partitioned by tiny step to obtain a series of path point. The finish point from the start point was connected by using straight line in sequence. To decrease the path length and turning angle, the path node can be removed if there are no obstacles on the line. The analysis and comparison between the proposed algorithm, traditional A* algorithm and another improved A* method were then given in the simulation experiment and physical experiments. Additionally, the merits of the proposed algorithm and other algorithms were compared when the obstacle rate, amount of task point, and step length were different. The experiment results show that the proposed algorithm effectively reduces the path length and turning angle.

mobile robot; path planning; A* algorithm; grid method

1674-2974(2017)04-0094-08

10．16339/j．cnki．hdxbzkb．2017．04．013

2016-07-25

国家科技支撑计划项目(2015BAF11B01),National Science and Technology Support Program(2015BAF11B01)；高等学校博士学科点专项科研基金资助项目(20130161110009),Specialized Research Fund for the Doctoral Program of Higher Education of China(20130161110009)；湖南省自然科学基金资助项目(14JJ1011),National Natureal Science Foundation of Hunan Province (14JJ1011)

孙炜(1975-)，男，河南淮滨人，湖南大学教授，博士†通讯联系人，E-mail:thwei2008@126.com

TP391.4

A