基于动态集成LSSVR的超短期风电功率预测
刘荣胜,彭敏放†,张海燕,万勋,沈美娥
(1. 湖南大学 电气与信息工程学院,湖南 长沙 410082;2. 国网湖南省电力公司电力科学研究院,湖南 长沙 410007;3. 北京信息科技大学 计算机学院,北京 100101)
基于动态集成LSSVR的超短期风电功率预测
刘荣胜1,彭敏放1†,张海燕1,万勋2,沈美娥3
(1. 湖南大学 电气与信息工程学院,湖南 长沙 410082;2. 国网湖南省电力公司电力科学研究院,湖南 长沙 410007;3. 北京信息科技大学 计算机学院,北京 100101)
针对最小二乘支持向量回归(Least Square Support Vector Regression,LSSVR)建模风电功率时变特性的局限性,提出了一种基于动态集成LSSVR的超短期风电功率预测模型.首先利用风电场监测控制与数据采集(Supervisory Control And Data Acquisition,SCADA)与数值天气预报(Numerical Weather Prediction, NWP)系统的历史数据建立离线单体LSSVR模型库,然后根据预测时段与训练时段NWP序列的相似度从单体LSSVR模型库中动态选择候选集成成员,再后综合考虑正确性与多样性确定集成成员.最后由预测时段与训练时段NWP序列间的相似度分配集成LSSVR成员的权重.通过对湖南省某风电场输出功率进行预测,验证了动态集成LSSVR预测模型的有效性,与持续法、自回归求和移动平均法、单体LSSVR模型、常权重LSSVR组合模型及BPNN动态集成模型相比,动态集成LSSVR模型具有更高的精度,在天气非平稳变化阶段更加明显.
超短期风电功率预测; 最小二乘支持向量回归;动态集成;动态时间弯曲距离;数值天气预报
风力发电是目前技术最成熟、最具商业开发前景的可再生能源发电技术之一[1],受风向、风速、气压、温度、海拔、地形地貌及风机特性等因素影响,其输出功率具有随机性和间歇性[1-2].风电大规模并入电力系统后,其随机性和间歇性会给电力系统的调度及稳定运行带来新的挑战[3-4].及时、准确的风电功率预测是大力发展风力发电的关键技术之一.国家能源局颁布的《风电场功率预测预报管理暂行办法》要求风电场必须及时上报短期与超短期风电功率预测(Ultra-short-term Wind Power Prediction, USTWPP)报告[5].
根据预测时效不同,风电功率预测可分为中长期、短期与超短期预测[6].USTWPP的预测时效为未来0~4 h,因时效短,精度要求高,对预测方法有更高的要求.风电功率预测的方法包括统计法[7-8]、物理法[9]、人工智能法[10]及组合预测法等.统计法依据风电场输出功率的变化趋势外推下一时刻的风电功率,常用的统计方法有持续法、移动平均法及自回归求和移动平均法等[11].统计法适合于气象信息有限的USTWPP,其建模简单、计算量少,可根据风电场的特点及位置调整预测模型,准确性较高,应用广泛[8];但统计法信息源单一,无法按不同的边界条件修正预测模型,健壮性差,在非平稳变化时段预测效果差.物理法基于数值天气预报(Numerical Weather Prediction, NWP)预测未来的气象数据,然后结合风电场周围的地形、地貌等,计算风电机组轮毂高度处的风速与风向,最后参照风机的功率转换曲线预测风电场的输出功率.物理法不需要大量历史数据训练模型,但我国用于风电的商业NWP起步较晚,需提高NWP的更新频率与时间分辨率,才能将物理法应用于USTWPP[7,10].风电场输出功率受诸多因素影响,机理复杂,难以建立准确的数学模型,为了提高USTWPP预测的准确性,人工神经网络(Artificial Neural network,ANN)、支持向量机(Support Vector Machine,SVM)及模糊逻辑等人工智能方法相继被用于USTWPP.ANN方法不需按机理建立数学模型,具有较好的非线性逼近能力和泛化能力,但需要大量的历史数据训练模型[12],ANN的层数及各层的节点数等只能依赖经验确定.SVM方法在处理小样本学习问题时具有良好的性能,但其适应性有待进一步研究[13],且不能建模时变系统.模糊逻辑可以处理风电功率的不确定性,但隶属函数选择依赖于历史数据与专家经验[14-15].
单一预测模型有其内在局限性,组合预测方法利用不同方法优势互补,提高预测模型的准确性和健壮性,已成为研究USTWPP的一种趋势.文献[16]提出了一种利用小波变换与SVM相结合的时频综合预测方法,减少了采样误差和噪声对预测结果的影响,但其没有利用NWP信息提高风电功率预测的准确性.ANN与SVM等模型的参数会影响USTWPP的准确性,借助遗传算法或粒子群优化算法可提高参数选取的效率和预测的准确性[17].基于权重组合的USTWPP方法将不同单体预测方法的预测值加权平均[18],其利用不同单体模型的优点,克服某一或多个因素对预测误差的集中影响,已成为国内外的研究热点.文献[18]在6种单体风电功率预测方法的基础上采用等权平均组合预测法、均方差倒数法和多层感知器智能算法作为组合方法的融合策略确定各单体模型所占权重.文献[19]通过最大信息熵原则确定每个单体模型的权重建立组合预测模型.文献[20]将风电功率组合预测看作一个信息融合问题,应用交叉熵理论设置各个预测模型的权重,建立风电功率组合预测模型.上述组合模型有效的提高了风电功率预测的准确性,但是没有考虑风电场所处环境的时变特性,上一时刻的最优组合,下一时刻未必最优.根据风电场的时变特性,建立动态组合预测模型,可提高USTWPP预测结果的准确性.本文提出一种基于动态集成最小二乘支持向量回归(Least Squares Support Vector Regression,LSSVR)的USTWPP模型.首先基于NWP与风电场监测控制与数据采集(Supervisory Control And Data Acquisition,SCADA)系统的历史数据离线建立单体LSSVR模型库;然后根据预测时段的NWP特征从单体LSSVR库中动态选择候选集成成员;再后综合考虑多样性与正确性确定集成LSSVR成员;最后各集成成员的权重由预测时段与训练时段NWP的动态弯曲时间(Dynamic Time Warping,DTW)距离给定.将动态集成LSSVR模型应用于湖南某风电场的输出功率预测,研究及实验证明了基于动态集成LSSVR的超短期风电功率预测模型的正确性和有效性,是计及风电场输出功率时变特性进行USTWPP的有益尝试.
1 基本理论
1.1 时间序列相似性
DTW对同步问题不敏感、计算精度高、可度量长度不同的时间序列间的相似性,下文基于DTW定义时间序列相似度.
定义1 DTW距离.时间序列X={x1,…,xm}与Y={y1,…,yn}的DTW距离Ddtw(X,Y)递归定义为:
如果X与Y均为空序列{},则Ddtw(X,Y)=0;
如果X与Y中有且仅有一个空序列{},则Ddtw(X,Y)=∞;
如果X与Y均不为{},则Ddtw(X,Y)如式(1):
Ddtw(X,Y)=d(x1,y1)+
(1)
其中d(x1,y1)=‖x1-y1‖2;rest(X)={x2,…,xm};rest(Y)={y2,…,yn};m,n分别为时间序列X与Y的长度.一般采用动态规划算法计算时间序列间的DTW距离,时间复杂度为O(N2)[21].
定义2 时间序列相似度.时间序列X与Y的相似度S(X,Y)如下:
(2)
其中θ为给定的相似度阈值,Ddwt(X,Y)为时间序列X与Y的动态时间弯曲距离.
1.2 最小二乘支持向量回归
设最小二乘支持向量回归问题的训练集Str={(x1,y1),…,(xk,yk),…,(xK,yY)},其中xk∈Rn为输入量,yk∈R为与xk对应的输出,k=1,…,K,K=|Str|为训练集的样本数.对训练集Str,LSSVR优化问题可表示如式(3)~(4)[22]:
(3)
s.t.yk=wTφ(xk)+b+ek,k=1,…,K
(4)
其中w为权向量,γ为正则化参数,ek为误差变量,b为偏置量,φ(·)为从输入空间到高维特征空间的非线性映射.
对应于最优化问题(3)~(4)的Lagrange函数如式(5):
(5)
其中αk为Lagrange乘子,对应于αk≠0的样本点称为支持向量.
式(5)的KKT条件如下:
(6)
(7)
(8)
(9)
其中k=1,…,K.
式(6)~(9)转换为式(10)所示的方程组
(10)
其中Y=(y1,…,yK)T,α=(α1,…,αK)T,I=(1,…,1)T,Ωi,j=φ(xi)Tφ(xj)=H(xi,xj),H为核函数,本文取高斯核函数,其如式(11).
(11)
其中σ为自变量x的分布方差.
解方程组(10)求得α与b,对于新的输入向量x,其对应的输出值y(x)如式(12):
(12)
2 基于动态集成LSSVR的USTWPP建模
计及风电场的时变特性,提高超短期风电功率预测的准确性,本文提出一种动态集成LSSVR模型,并将其应用于超短期风电功率预测,该模型包括3个步骤:
第1步,离线构建单体LSSVR模型库;
第2步,动态选择集成LSSVR成员;
第3步,基于DTW的权重分配.
2.1 构建单体LSSVR模型库
基于动态集成LSSVR的USTWPP根据风电场的时变特性,动态重构集成LSSVR模型.单体LSSVR是集成LSSVR的基础,为提高集成LSSVR动态重构的速度,利用历史数据构建离线单体LSSVR模型库.单体LSSVR模型库构建流程如图1所示.包括数据预处理、子序列划分、NWP降维、样本集构造及单体LSSVR创建等5个步骤.
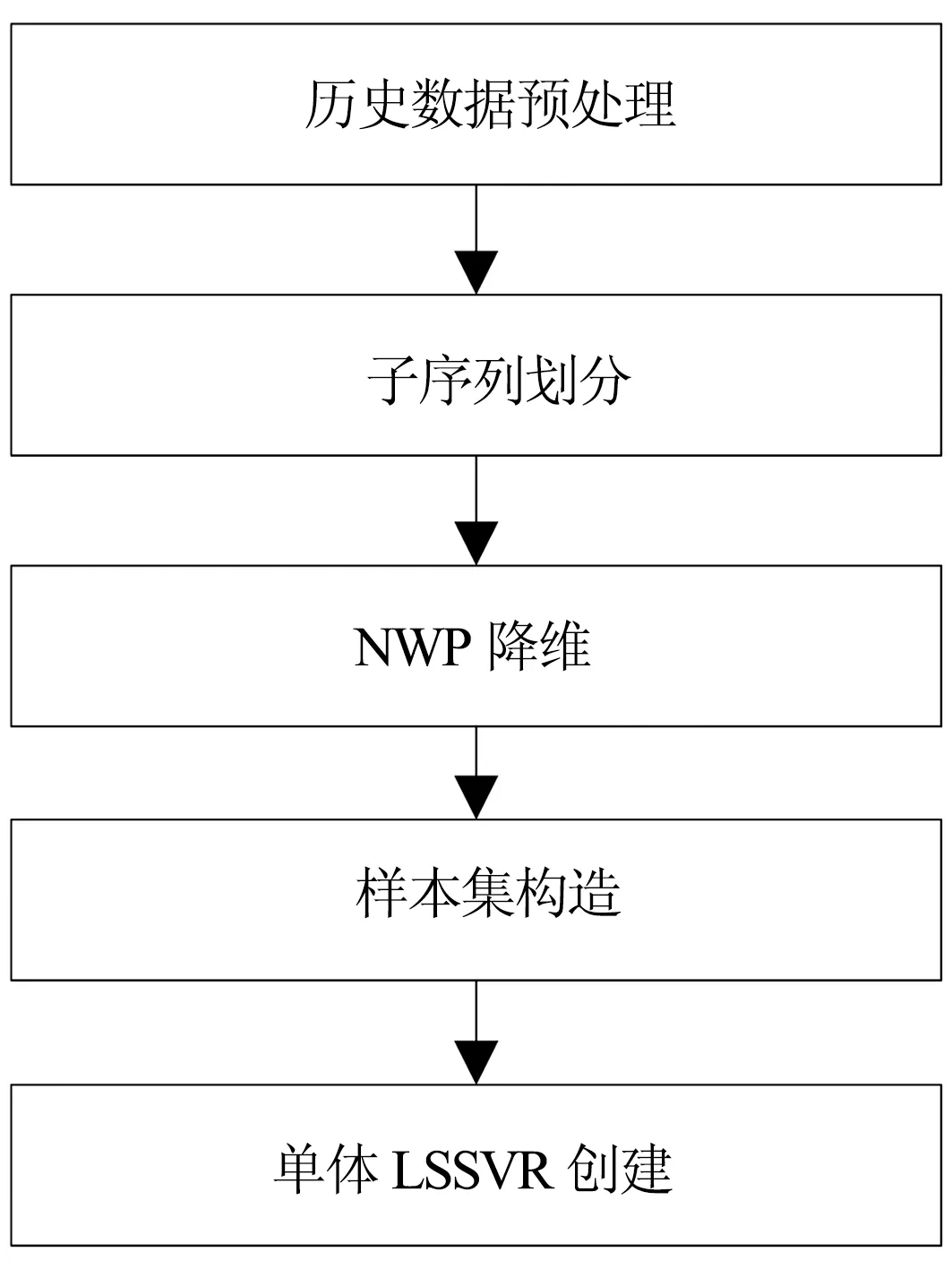
图1 LSSVR模型创建流程图
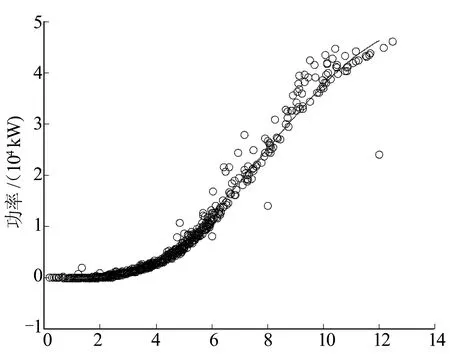
1)数据预处理:风电场SCADA系统以15 min 1次的频率采集风电场测风塔的风速及输出功率.图2为湖南某风电场SCADA系统测得的2013年9月风速与输出功率关系图.风速低于切入风速时,输出功率为0;风速高于额定风速后,风电场的输出功率为额定装机容量;风速在切入风速与额定风速之间时,功率与风速之间呈3次函数关系.但是受设备故障或计划检修等因素影响,输出功率在某些时刻远离风速-功率拟合曲线,该类数据会影响风电场功率预测的准确性,用其临近2个时刻的平均风速与输出功率矫正.网络和数采系统故障可能导致数据丢失,如果连续丢失的数据点在5个以上,则将其从历史数据中删除,否则用均值法对缺失的数据进行补全.
2)子序列划分:NWP及SCADA系统积累了大量的历史数据,以全部历史数据训练LSSVR模型,会因为训练样本规模过大,使得式(10)求解困难,导致过拟合,泛化能力差.因此将历史数据划分成长度为L的等长子序列,用各子序列单独训练模型.
3)NWP降维: NWP信息中包含风速的x轴分量u,y轴分量v,气压p和温度t等,USTWPP预测时效短,温度变化较小,建模时只选取u,v与p.每个子序列的NWP信息可表示成一个如式(13)所示的L×3矩阵M,其中L为子序列的长度;经式(14),式(15)将矩阵M变换成向量Z.
风速/(m·s-1)
(13)
C=MT×M
(14)
(15)
其中e为与矩阵C最大特征值对应的特征向量.
4)构建样本集:单体LSSVR模型的样本集表示如下:
Ssmp={(xi,yi)|i=1,…,N}
(16)
其中N=|Ssmp|为样本集Ssmp的样本数,xi为第i个样本的输入,yi为与xi对应的输出.创建样本集Ssmp的关键是确定xi与yi.
影响风电场输出功率的因素包括地形地貌、风电机组排列、风机型号、海拔、风向、风速、温度、气压及空气密度等,其中地形地貌、风机排列、风机型号及海拔等为非时变因素,风向、风速、温度、气压及空气密度为时变因素.将风电场抽象成如图3所示的能量转换系统,时变因素作为系统输入,在时变因素作用下,向外输出电能,输出功率由输入(时变因素)与系统共同(非时变因素)决定.不同输入作用于系统,系统上可获得不同的监测信息,监测信息可以反映系统的功率输出.而风电场的NWP与SCADA系统信息就是能量转换系统的监测信息,其反映了风电场输出功率的变化规律.计及风速与功率成强相关性,只将风电场当前的NWP与上一时刻的输出功率作为输入,下一时刻的输出功率作为输出.样本的输入xi=

图3 风电场能量转换原理图
5)单体LSSVR创建:用各子序列生成的样本集Ssmp分别训练LSSVR模型,将全体单体LSSVR模型及其训练子序列存入数据库建立单体LSSVR预测模型库.
2.2 集成成员选择
集成成员的多样性与正确性是构建高质量集成LSSVR模型的基础,为建模风电场的时变特性,根据预测时段的NWP信息,动态的从单体LSSVR模型库中选择预测时段与训练时段NWP相似度最高的Q个单体LSSVR作为集成成员候选集D,集成成员集D′必须满足:D′⊆D,且ψ(D′)有最大值[23].
(17)
其中λ∈[0,1]为多样性和正确性的调节因子,若λ=1,则只考虑正确性,若λ=0,则只考虑多样性.fi与fj均为单体LSSVR模型,A(fi)为单体LSSVR模型fi的预测准确率,其计算如下式:
(18)
其中yi为风电功率实测值,f(xi)为与输入xi对应的预测值,Ste为测试集.
kp(fi,fj)为单体LSSVR模型fi与fj的差异性度量指标——成对Kappa(Pairwise-kappa,kp)[24],其计算如式(19).
kp(fi,fj)=
(19)
经典kp指标用于度量分类器的差异性,为使其可度量回归模型的差异性,对fi与fj的联合进行了改进,改进后的联合分布如表1所示.
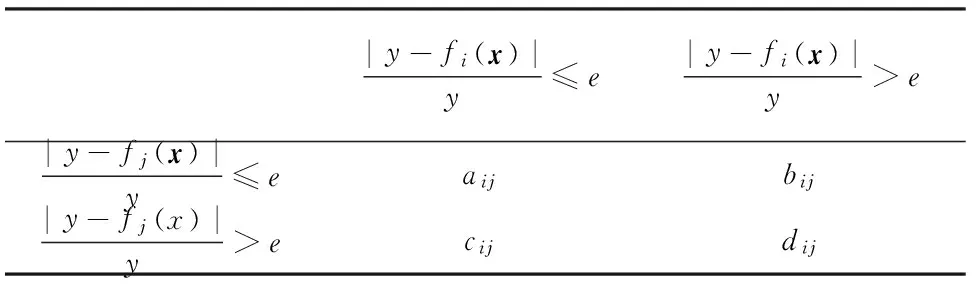
表1 LSSVR模型fi与fj的联合分布
aij为fi与fj的相对误差均不大于允许误差e的样本数;bij为fi的相对误差大于允许误差e,而fj的相对误差不大于允许误差e的样本数;cij为fj的相对误差大于允许误差e,而fi的相对误差不大于允许误差e的样本数;dij为fi与fj的相对误差均大于允许误差e的样本数.
2.3 权重分配
集成成员权重分配是将多个单体LSSVR组合成高效集成预测模型的关键.风电场具有时变特性,上一时刻最适合的权重分配,在下一时刻不一定适应,为了适应风电场的变化,根据NWP的时变特性动态分配LSSVR集成预测模型的权重.
预测时段的NWP序列经降维后记为NWP0,单体LSSVRi训练时段的NWP序列经降维后记为NWPi.由式(2)计算NWP0与NWPi的相似度S(NWP0,NWPi),集成预测成员LSSVRi的权重如下:
(20)
对于新的输入xi,其对应的风电功率预测结果为:
(21)
3 实验及其结果分析
3.1 实验环境与数据
试验平台采用Matlab7.10.0(R2010a),在其上安装libsvm软件包用于单体LSSVR建模.数据包括两部分:数值天气预报与风电场历史监测数据.NWP来自丹麦某气象公司,时间分辨率为15min,某时刻的历史NWP数据为其最后一次更新的值.历史NWP信息如表2所示,包含了风速的x轴方向分量、y轴方向分量及气压.

表2 某风电场NWP历史数据
风电场历史监测数据来自于其SCADA系统,时间间隔为15 min.风电场的装机容量为48 MW,2013年9月某日经归一化处理后的日功率曲线如图4所示.误差评价指标采用平均百分比误差(MAPE)[25].

时间/刻
3.2 实验结果与分析
以湖南某风电场2012年9月1日至2013年8月31日的NWP及其实际输出功率为历史数据训练单体LSSVR模型.共35 040组数据,经数据预处理删除连续丢失数据的情形,得33 574组有效数据,子序列长度分别为4 h,8 h,12 h,24 h, 3 d及7 d时,训练时段与预测时段NWP序列间DTW距离与单体LSSVR模型预测误差的关系如图5所示.虽然划分子序列的长度不同,但预测误差均随训练时段与预测时段NWP序列间DWT距离的增大而增大,两者成正相关,且只有DWT较小的单体LSSVR模型的预测结果能够满足规范的要求.试验结果说明预测时段与训练时段间NWP相似度越高,越有利于提高单体LSSVR预测模型的精度.

图5 LSSVR预测误差与数值天气预报DTW距离关系图
当子序列时段长度L分别为4 h,8 h,12 h,24 h,3 d及7 d时,与预测时段NWP相似度最的单体LSSVR模型预测的结果如图6所示,当训练时段与预测时段的NWP相似度较高时,各LSSVR模型预测值围绕实测值上下波动,LSSVR模型能够较好地学习预测时段风电输出功率的变化规律, 说明了基于NWP相似度构建单体LSSVR模型的有效性.

时间/刻
子序列时段长度L分别取4 h,8 h,12 h,24 h,3 d及7 d时,最优单体LSSVR模型预测误差的统计结果如表3所示.

表3 不同L单体LSSVR比较
表3显示:L过小,单体LSSVR模型的训练样本过少,预测精度不高,增加L,单体LSSVR的预测精度逐步提高,但是当L太大时,NWP的准确率会下降.当长度L为24 h时,单体LSSVR模型具有最优的预测效果.构建离线LSSVR库时,设定子序列的长度L为24 h.
集成成员多样性与正确性调节因子λ是影响集成预测结果的另一个重要因素,当L为24 h时,λ与预测误差的统计结果如表4所示,统计结果显示λ取0或1时,只计及了集成成员的正确性或者多样性,预测误差比较大,当其取值为0.6时,正确性与多样性取得最好的平衡,预测效果最佳.
取λ=0.6,L=24 h时,集成预测试验结果如图7所示,动态集成预测模型与单体模型都能有效地预测风电场输出功率.进一步地对2013年9月输出功率预测结果进行统计,统计结果如表5所示,表5中Best表示集成模型中最好的单体LSSVR预测结果,Worst为集成成员中最差的单体LSSVR预测结果,Average为集成成员预测结果的平均误差, DELSSVR为动态集成LSSVR预测结果的误差统计结果.统计结果显示:DELSSVR预测模型的MAPE小于集成成员的平均MAPE,也小于最好的单体LSSVR的MAPE.验证了基于动态集成LSSVR的USTWPP模型的有效性,其比最好的单体LSSVR模型预测误差更小.

表4 λ与动态集成预测误差关系

时间/刻
表5 集成预测误差分析
Tab.5 The error analysis of ensemble LSSVR model %

WPPModelMin-MAPEMax-MAPEAvg-MAPEBest1.3321.1912.31Worst0.3927.7015.73Average0.9923.2713.53DELSSVR1.1222.259.03
基于DELSSVR的USTWPP模型与其它常用的USTWPP预测模型的对比试验结果如表6所示.其中PM表示持续法,ARIMA为自回归移动平均法,CWLSSVR为常权重LSSVR集成预测模型,DEBPNN为文献[25]中神经网络动态集成预测模型,DELSSVR为本文的动态集成LSSVR模型.DELSSVR模型利用了风电场NWP序列的时变特性,动态实现集成成员选择与权重分配,与其它方法相比,提高了USTWPP的准确性,在非平稳阶段,尤为明显.
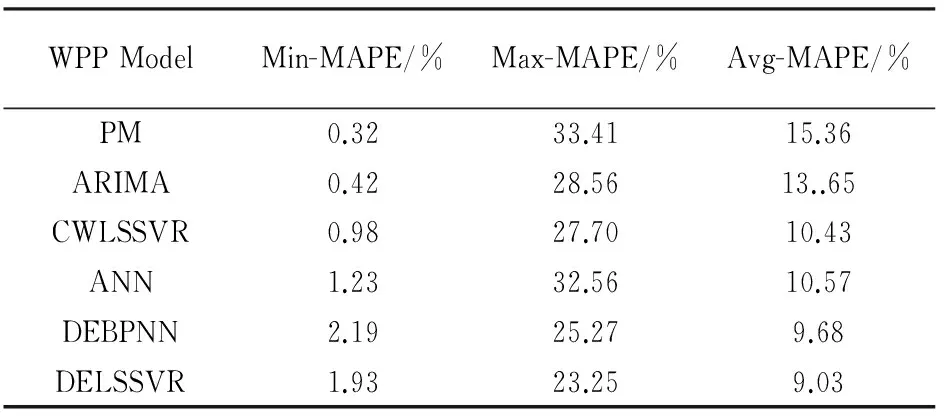
表6 不同预测模型对比试验
4 结 论
计及风电场的时变特征,本文提出了一种基于动态集成LSSVR的USTWPP模型,并将该模型应用于超短期风电功率预测.研究和实验得出如下结论:
1)风电场输出功率规律受外部天气环境影响,具有时变特性,建立时变模型有利于提高风电功率预测的准确性.
2)由历史数据建立离线单体LSSVR模型库的方式,可减少集成LSSVR动态重构的计算量,提高构建动态集成LSSVR的速度.
3)动态集成LSSVR模型基于预测时段NWP的时变特征动态选择集成成员与分配权重,其能够更好地建模风电功率的时变特性,提高USTWPP的预测精度.
[1] 薛禹胜,雷兴,薛峰,等.关于风电不确定性对电力系统影响的评述[J].中国电机工程学报, 2014, 34(29):5029-5036.
XUE Yusheng, LEI Xing, XUE Feng,etal. A review on impacts of wind power uncertainties on power systems [J]. Proceedings of the CSEE, 2014, 34(29): 5029-5036.(In Chinese)
[2] KUSIAK Andrew,ZHANG Zijun.Short-horizon prediction of wind power:A data-driven approach[J].IEEE Transactions on Energy Conversion, 2010, 25(4):1112-1122.
[3] 王成山,高菲,李鹏,等.低压微网控制策略研究[J].中国电机工程学报, 2012, 32(25):2-8.
WANG Chengshan, GAO Fei, LI Peng,etal. Control strategy research on low voltage microgrid[J]. Proceedings of the CSEE, 2012, 32(25): 2-8.(In Chinese)
[4] 李培强,王继飞,李欣然,等. 双馈与直驱风电机组的小干扰稳定性对比分析[J].湖南大学学报:自然科学版, 2014, 41(1):92-97.
LI Peiqiang, WANG Jifei, LI Xinran,etal. Analysis on the impact of DFIG and DDSG wind plant on the small signal stability of the power system[J]. Journal of Hunan University:Natural Sciences, 2014,41(1): 92-97.(In Chinese)
[5] 薛禹胜,郁琛,赵俊华,等. 关于短期及超短期风电功率预测的评述 [J].电力系统自动化, 2015,39(6):141-151.
XUE Yusheng, YU Chen, ZHAO Junhua,etal. A review on short-term and ultra-short-term wind power prediction[J]. Automation of Electrical Power Systems, 2015,39(6):141-151.(In Chinese)
[6] SHI Jie,DING Zhaohao,LEE Weijen,etal.Hybrid forecating model for very-short term wind power forecasting based on grey relational analysis and wind speed distribution features[J].IEEE Transactions on Smart Grid, 2014, 5(1):521-526.
[7] 王贺, 胡志坚, 陈珍,等.基于集合经验模态分解和小波神经网络的短期风功率组合预测[J].电工技术学报, 2013, 28(9):137-144.
WANG He, HU Zhijian, CHEN Zhen,etal. A hybrid model for wind power forecasting based on ensemble empirical mode decomposition and wavelet neural networks[J]. Transactions of China Electrotechnical Society, 2013,28(9): 137-144 .(In Chinese)
[8] 周松林, 茆美琴,苏建徽.风电功率短期预测及非参数区间估计[J].中国电机工程学报, 2011, 31(25):10-16.
ZHOU Songlin, MAO Meiqin, SU Jianhui. Short-term forecasting of wind power and non-parametric confidence interval estimation [J]. Proceedings of the CSEE, 2011, 31(25): 10-16.(In Chinese)
[9] NIMA Amjady,FARSHID Keynia, HAMIDREZA Zareipour.Wind power prediciton by a new forecast engine composed of modified hybrid neural network and enhanced particle swarm optimization[J].IEEE Transactions on Sustainable Energy, 2011, 2(3):265-276.
[10]CHEN Niya,QIAN Zheng,NABNEY Ian T,etal. Wind power forecasts using gaussian processes and numerical weather prediction [J].IEEE Transactions on Power Systems, 2014, 29(2):656-665.
[11]陶佳,张弘,朱国荣,等.基于优化相空间重构技术的风电场发电功率预测研究[J].中国电机工程学报, 2011, 31(28):9-14.
TAO Jia, ZHANG Hong, ZHU Guorong,etal. Wind power prediction based on technology of advanced phase space reconstruction[J]. Proceedings of the CSEE, 2011, 31(28):9-14.(In Chinese)
[12]陈志宝,丁杰,周海,等.地基云图结合径向基函数人工神经网络的光伏功率超短期预测模型[J].中国电机工程学报, 2015,35(3):561-567.
CHEN Zhibao, DING Jie, ZHOU Hai,etal. A model of very short-term photovoltaic power forecasting based on ground-based cloud images and RBF neural network[J]. Proceedings of the CSEE, 2015 ,35(3):561-567. (In Chinese)
[13]陈妮亚,钱政,孟晓风,等.基于空间相关法的风电场风速多步预测模型[J].电工技术学报, 2013, 28(5):15-21.
CHEN Niya, QIAN Zheng, MENG Xiaofeng,etal. Multi-step ahead wind speed forecasting model based on spatial correlation and support vector machine[J]. Transactions of China Electrotechnical Society, 2013, 28(5):15-21 .(In Chinese)
[14]Subhagata Chattopadhyay,Dilip Kumar Pratihar, Sanjib Chandra De Sarkar,etal. Fuzzy-logic-based screening and prediction of adult psychoses:A novel approach[J].IEEE Transactions on System,Man,and Cybernetics—Part A:System and Humans, 2009, 39(2):381-387.
[15]王贺,胡志坚,仉梦林,等.基于模糊信息粒化和最小二乘支持向量机的风电功率波动范围组合预测模型[J].电工技术学报, 2014, 29(12):218-224.
WANG He, HU Zhijian, ZHANG Menglin,etal. A combined forecasting model for range of wind power fluctuation based on Fuzzy information granulation and least squares support vector machine [J]. Transactions of China Electrotechnical Society, 2014, 29(12):218-224. (In Chinese)
[16]田中大,李树江,王艳红,等.基于小波变换的风电场短期风速组合预测[J].电工技术学报, 2015, 30(9):112-120.
TIAN Zhongda, LI Shujiang, WANG Yanhong,etal. Short-term wind speed combined prediction for wind farms based on wavelet transform [J]. Transactions of China Electrote Chnical Society, 2015, 30(9): 112-120. (In Chinese)
[17]王振树,卞绍润,刘晓宇,等.基于混沌与量子粒子群算法相结合的负荷模型参数识辨研究[J].电工技术学报, 2014, 29(12):211-217.
WANG Zhenshu, BIAN Shaorun, LIU Xiaoyu,etal. Research on load model parameter identification based onthe CQDPSO algorithm [J]. Transactions of China Electrotechnical Society, 2014, 29(12): 211-217 .(In Chinese)
[18]BOUZOU H, BENOUDJIT N. Multiple architecture system for wind speed prediction [J]. Applied Energy, 2011,88(7):2463-2471.
[19]HAN S, LIU Y, LI J. Wind power combination prediction based on the maximuminformation entropy principle [C] //World Automation Congress. June 24-28, 2012, Puerto Vallarta, Mexico:4p.
[20]陈宁,沙倩,汤奕,等. 基于交叉熵理论的风电功率组合预测方法[J]. 中国电机工程学报,2012,32(4):29-34.
CHEN Ning, SHA Qian, TANG Yi,etal. A combination method for wind power prediction based on cross entropy theory[J]. Proceedings of the CSEE,2012, 32(4):29-34. (In Chinese)
[21]李海林,杨丽彬.基于增量动态时间弯曲的时间序列相似性度量方法[J].计算机科学, 2013, 40(4):227-230.
LI Hailin, YANG Libin.Similarity measure for time series based on incremental dynamic time warping[J]. Computer Science, 2013, 40(4):227-230. (In Chinese)
[22]WOOJIN Kim, JAEMANN Par, JAEHYUN Yoo,etal. Target localization using ensemble support vector regression in wireless sensor networks[J]. IEEE Transactions on Cybernetics, 2013, 43(4):1189-1198.
[23]杨春, 殷绪成, 郝红卫, 等. 基于差异性的分类器集成:有效性分析及优化集成[J].自动化学报, 2013, 40(4):661-674.
YANG Chun, YIN Xucheng, HAO Hongwei,etal. Classier ensemble with diversity: effectiveness analysis and ensemble optimization[J]. Acta Automatica Sinica, 2013, 40(4): 661-674.(In Chinese)
[24]李洪超, 王伟刚, 董雪梅, 等. 基于 M-LS-SVR 的变压器油中溶解气体浓度预测[J]. 电气技术, 2016, 1(2): 76-80.
LI Hongchao, WANG Weigang, DONG Xuemei,etal. Concentration prediction of dissolved gasesin transformer oil based on M-LS-SVR[J].Electrical Technology, 2016, 1(2): 76-80. (In Chinese)
[25]何东, 刘瑞叶. 基于主成分分析的神经网络动态集成风功率超短期预测[J]. 电力系统保护与控制, 2013, 41(4): 50-54.
HE Dong, LIU Ruiye. Ultra-short-term wind power prediction using ANN ensemble based on the principal components analysis[J].Power System Protection and Control, 2013, 41(4): 50-54. (In Chinese)
Ultra-short-term Wind Power Prediction Based on Dynamical Ensemble Least Square Support Vector Regression
LIU Rongsheng1,PENG Minfang1†,ZHANG Haiyan1,WAN Xun2,SHEN Meie3
(1. College of Electrical and Information Engineering, Hunan University, Changsha 410082, China;2. State Grid Hunan Electric Power Company Electric Power Research Institute, Changsha 410007, China; 3. Computer School Beijing Information Science & Technology University, Beijing 100101, China)
For the limitation of least square support vector regression (LSSVR) in modeling the time varying feature of wind power, an ultra-short-term wind power prediction (USTWPP) model based on dynamical ensemble LSSVR was proposed. Firstly, the off-line LSSVR model library was created by making use of the historical data which were obtained from Numerical Weather Prediction (NWP) and supervisory control and data acquisition (SCADA) system of wind farm. Then, the candidate members of ensemble LSSVR were selected from off-line LSSVR model library dynamically according to the similarity between the NWP of forecasting period and the NWP of training period. The ensemble members were decided by considering the accuracy and diversity. Finally, the weights of ensemble LSSVR members were assigned according to the similarity between the NWP of training and NWP of prediction period. The validity of the dynamical ensemble LSSVR based predictor was verified by predicting the wind power of a wind farm in Hunan Province. Compared with persistence method (PM), auto regressive integrated moving average (AGIMA), LSSVR, constant weight ensemble LSSVR, and ensemble artificial neural networks (ANN), the dynamical ensemble LSSVR is more accurate, especially when the weather changes severely.
ultra-short-term wind power prediction; least square support vector regression; dynamical Ensemble; dynamical time warp; numerical weather prediction
1674-2974(2017)04-0079-08
10.16339/j.cnki.hdxbzkb.2017.04.011
2016-08-12
国家自然科学基金资助项目(61472128;61173108),National Natural Science Foundation of China(61472128;61173108)
刘荣胜(1981-),男,湖南娄底人,湖南大学博士研究生†通讯联系人,E-mail:921173232@qq.com
TM614
A

