数学课堂也能诗意盎然

江苏省苏州第十中学 陈 蕾

数学课堂也能诗意盎然

江苏省苏州第十中学 陈 蕾

“诗性教育”是一种以“浸润”和“体验”为特征的教育，它让教育成为一种自然的流露和呈现，并以“本真、唯美与超然”为基本特征。它是以学生的健康、快乐、自由发展为第一位的；是以学生必须有继承和创造优秀文明的文化自觉的态度、情感、行动为前提的；是以学生学会了解、敬畏、欣赏和创造“美”为使命的。那么， 如何在数学课堂上体现诗性教育的理念呢？我将从以下两方面进行阐述。

一、数学课堂外在的“诗性”

数学课堂要有诗性，就是要让数学课堂成为一道诗情画意的风景线，数学教师犹如导游，使学生在学习过程中犹如游览名胜，处处得到美的享受，这就必然会激发他们的学习兴趣，调动他们学习的积极性，培养学生的创新能力。诗性的数学课堂就成了学生学习数学、探究数学的理想平台。

1.让数学变得“好看”

在等比数列的一堂课上，我讲了德国数学家科赫（H．V．Koch）创造的雪花曲线：以一个基础等边三角形边长的三分之一为边的小等边三角形迭加到六角星，再把六角星缩为三分之一迭加到六角星的每个小三角形处，……如此叠加下去便得到如图4所示的雪花图案：

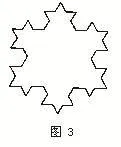
图4

由此，我还拓宽了一下学生的知识面，介绍了一门数学分支——分形几何，给学生展示了分形的很多图片，学生们都惊叹不已，原来数学可以这么好看。

2.让数学变得“好听”

诗性之美美在意境，虽寥寥数语，却能勾画出万千风情。我常常会搜集一些很有意思的数学诗歌运用于课堂上，效果非常好。

比如诗歌《我的向量》：

给你一个方向/ 你就成为我的向量/ 给你一个坐标系/你就在我心空飞翔/给你一个基底/ 带着我，征途起航/繁复的几何关系/变成纯代数的情殇/优美的动态结构/没有人情冷暖世态炎凉/ 哪怕山高路远/哪怕风雨苍茫/不管起点在哪里/你始终在水一方。

再例如学习双曲线和渐近线的时候，可以给学生听一首流行歌曲《悲伤的双曲线》来加深印象：

如果我是双曲线/你就是那渐近线/如果我是反比例函数/你就是那坐标轴/虽然我们有缘/能够生在同一个平面/然而我们又无缘/慢慢长路无交点/为何看不见/等式成立要条件/难到正如书上说的/无限接近不能达到/为何看不见/明月也有阴晴圆缺/此事古难全/但愿千里共婵娟。

学习了有关概念，再配上这样的诗歌、这样的歌曲，学生会觉得妙不可言，因为只有学了这些概念，你才能读懂这些语句，读懂这些语句里只可意会不可言传的东西，于是学生都会对我会心一笑。

3.让数学变得很“生活”

诗性之美美在生活的底蕴，正因为有了丰满的生活背景，诗歌才能如此深得人心，我们也应让数学教学密切联系学生的生活实际，利用实在、有趣的生活情景唤起学生对数学的信赖。

比如讲到同体积的球、正方体、圆柱哪个表面积最小的时候，我就问学生：“为什么泡泡吹出来总是球形的?”学生都会觉得很好奇，因为他们从来都没想过这个简单的现象，结合物理里的表面张力，稍一解释，学生豁然开朗，同时牢牢地记住了“同样体积的东西，球的表面积最小”的结论。

要做到以上三点， 难， 也不难，“不难”在于只要我们多用心、多积累，总能找到这样的好例子、好诗句、好故事。“难”在于我们不可能每堂数学课都能找到这样的诗情画意，都能上得如此华丽。所以这样的“诗性”让我觉得不踏实，一定还有更本质的“诗性”。

二、数学课堂本质的诗性

对每一届学生我都会问同样一个问题：“你觉得数学课能带给你什么？”学生的答案无非是公式、概念、定理等等，等他们说完了以后我会说：“若干年后，等你把公式、概念、定理都忘了以后，剩下的东西就是数学所给予你的。”学生就会说：“那就什么也没了。”我说：“还有你的思想方法和思维方式，数学对你们的影响是潜移默化的，你甚至感觉不到你思想上的变化是数学带给你的，学数学和不学数学的人考虑问题的方式肯定不一样，为什么学哲学、计算机、经济学到最高端的很多都是学数学出身的，就是这个道理。”诗性的数学课堂就是让学生可持续发展，让学生终身受益。这也正是功利课堂所不能比拟的。

在现实的学习过程中，我们把太多的精力投注到学生的基本知识、基本技能的训练上。为了让学生获得一本书、一章甚至一节的高分，让学生去背、去记大量重复的复杂的题目，还可能认为这是为学生好，是为学生的前途着想。实际上，学生一直这样才会真的没有前途。对学生心灵成长（而不仅仅是知识成长）有影响的课堂才是最有效的，在数学课上创设一个自由自在、异想天开的灵性世界，让数学课堂生成一种诗性的美，扎根在学生的心里。学生可持续发展的关键之所在就是在探索求知的过程中学会归纳、反思、验证、升华、补充、完善；学会发现问题，解决问题，最后形成一种性格，一种智慧。

1.构建符合学生认知规律的“五有”环节

学生的认知是一个由简单到复杂，由现象到本质逐步深化升华的过程，正确的教学方法应引导学生主动以“实践、探索、体验、碰撞、发现”为中心进行自主探索式学习，使学习过程成为沿着知识发生和发展过程的再实践、再探索、再体验、再验证、再发现的创造性活动。从感受困惑不解，提出问题，展开讨论，然后试着对这些问题寻找出答案中培养学生的创新精神和实践能力。教师的作用是安排教学活动顺序，将知识结构、学科规律的特点逐步内化到学生的认知结构中，促进学生认知能力的全面发展。为此，在教学实践中，我对学生知识的学习提出“五有”要求，即有见解，有验证，有整理，有归一，有反复。

首先，每一个问题要培养学生有自己的见解，这种见解哪怕是错误的，也是可贵的，然后引导学生通过验证推翻自己的错误，形成新的正确见解，如此循环往复，必将造就学生强大的头脑。例如：在讲双曲线定义的时候，学生会与椭圆类比，得到“到两个定点的距离的差为定值的点的轨迹”。不加绝对值，就是双曲线的一支，于是让学生完善；如果定值等于定点之间的距离，那又不对了，于是再总结再完善。学生如果掌握了这一学习原则，也就养成了求实、说理、批判、质疑等理性思维的习惯和锲而不舍的追求真理的精神，对他一生将多么重要。每节课如何遵循形成观念（归纳总结），验证观念（补充完善），升华观念（回忆以前，找出知识间的类似），形成学力，这是我们研究的关键之所在。

2.渗透数学的文化价值，培养学生具有可持续发展的意识

相对于数学作为纯粹的工具作用而言，我们应当更加重视数学的文化价值，包括积极地促成这样一种生活态度的养成，即努力超越世俗并追求更高层次上的快乐与人生价值。这就要求我们培养学生可持续发展的意识。学生可持续发展的意识包括思想品德素质、情感态度、价值观等，

数学对学生的影响是潜移默化的，让学生知道这种变化非常重要．比如讲完了集合与简易逻辑，我问学生有什么体会．他们说高中数学比初中数学难多了，因为许多题目都要进行分类讨论，刚开始很不适应，总是考虑不全面，或者就是分类出现重复，不过一个多月下来已经好多了．我于是开始渗透数学观念：“这种分类思想使得我们考虑问题更细致、更全面，这就是数学使人精密的道理，这是你们终身受用的东西．我们做大量的题目，关键不在于题目本身，而在于通过做题训练思维．”这么一说，学生觉得很有道理，自然就会对数学多一份好感。

在数学教学过程中，我认为不仅要让学生知道学习数学是很有用的，还应让他们知道具体有益在哪里，这样才能使他们心服口服，真正接受数学、喜欢数学，变被动为主动，从而学好数学。

再比如，讲完雪花曲线后，考虑到分形是电脑和数学的产物，可用电脑对数学式子进行无数次“迭代”来产生和“繁殖”。在描绘海岸线、云彩、人口分布、电影场景时都会起作用，即在生态学、天文学、气象学、电影摄像学及经济学等方面都能找到分形的应用。为让学生体会分形的应用，我布置了“收集有关分形的应用的资料并写一篇小论文”的作业，学生通过收集、整理材料，交出的论文质量超乎我的预料，这就证实了只要我们有效引导，学生的探究能力是无穷的。这是课题学习的教学，学生这方面经历比较少，我们老师自己经验也不足，加上课题学习大多内容与考试关系不大，所以课题学习的教学并没有引起大多数老师的重视，但为了学生长远的发展，为了激发学生学习数学的兴趣，体会数学的应用价值和文化价值，我们必须重视课题学习部分内容的教学，通过不断尝试进行有益的探索与实践。

把数学课堂与育人结合起来，针对学生的个性特点去开展我们的数学教学。遇到问题要想办法解决，以自己的意志、信念和智慧去战胜它。培养学生不怕困难、自信、自强、自立、锲而不舍的探索精神。数学中的逻辑推理要求我们追本溯源，凡事都要问个为什么，而不能靠想象去解决问题，培养学生不唯书不唯上、严谨求实、坚持真理、修正错误的作风。让学生体会到数学的这些特点，对他们严格要求，帮助他们树立正确的人生观和价值观，对他们将来做人、做事都有很大的帮助。 “我从孩子们的日记中看到他们分析事理的能力愈来愈强；从课堂中听到他们使用的词汇愈来愈清晰有理；从同学们的互动中感觉到容忍与爱心的滋生，一切的一切，让我觉得不只是与他们共同讨论数学而已，重要的是培养一个会做理性批判思考、会主动学习、会容忍异己欣赏别人以及有世界观的国民”， 这段话语正是数学培养学生可持续发展意识的最好印证。

数学课堂的诗性不仅立体地存在于整个教学过程中看得见的“三维空间”，而且还真实、长久地隐蔽存在于“四维空间”，即学生的心灵。

诗性的数学课堂是一种拨动心扉的力量，一种播种心田的艺术、一种陶冶心灵的美，让我们用全部感情去谱写每一节教案，让我们的数学课堂诗意盎然。