大圆筒围堰在各重要施工阶段的稳定性数值模拟

邢英薇

摘 要：基于有限元分析方法，分别评估某人工岛大圆筒围堰结构在三个重要施工阶段的稳定性。文中建立了不同施工阶段下大圆筒围堰结构及其土体的“结构-地基相互作用”有限元模型，根据有限元数值模拟结果，最终计算得到在各阶段下大圆筒围堰结构的稳定安全系数Kα均大于1，表明结构安全。同时，文中分别计算并分析了大圆筒围堰结构在不同阶段下的最大位移smax及其出现位置。研究成果可为类似工程的设计提供一定的技术支撑。

关键词：大圆筒围堰 重要施工阶段 稳定性 数值模拟

1.工程概况

某人工岛工程采用大圆筒作为其主要的围堰结构，另在其外、内两侧分别抛填块石和中粗砂斜坡堤，以保证其整体结构的稳定性。图1为大圆筒围堰的初步设计简化图式。在其施工过程中，主要包含三个重要的施工阶段：（a）第一阶段：打设大圆筒至强风化岩层中（筒底标高-29.0m），该阶段结构所受的外荷载为波浪力+剩余水压力；（b）第二阶段：抛填外侧块石斜坡堤，其外荷载为外侧斜坡堤产生的土压力+剩余水压力；（c）第三阶段：抛填内侧中粗砂斜坡堤，外荷载为内、外侧斜坡堤产生的土压力+剩余水压力。综上，本文针对图1中所示的（a）、（b）、（c）三个重要施工阶段，建立大圆筒围堰及其周围土体的有限元模型，基于有限元数值模拟的计算结果，利用加载系数法评估大圆筒围堰的整体稳定性。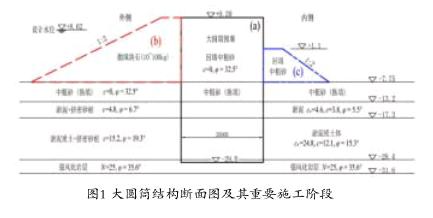

2.大圆筒围堰在各施工阶段下稳定性分析

2.1大圆筒围堰的有限元模型

在有限元分析过程中，大圆筒结构采用弹性模型，地基土体则采用Coulomb-Mohr模型。在结构与土体的接触区域设置主从接触面（结构为主、土体为从），接触面的本构模型在法向采用硬接触，在切向采用Coulomb摩擦模型。土体的计算域在水平方向上分别向大圆筒两侧各取5D=100m（D为大圆筒直径），在竖直方向上取至中风化层底部，为44m。如图2所示，分别为前文所述三个重要施工阶段下大圆筒围堰的有限元数值模型。

2.2外荷载计算

2.3大圓筒围堰稳定性评估标准

本文中通过定义一个加载系数α=F/FD来评估不同施工阶段大圆筒围堰结构的稳定性。其中，F为有限元计算时各分析步下所施加的荷载；FD为设计荷载（其值为外荷载）。当F加载到整体结构的极限承载力Fu时，如果α>1，表明结构极限承载力大于外荷载，结构安全；如果α=1，表明结构处于极限状态；而当α<1，表明结构极限承载力小于外荷载，结构不安全。因此，当F加载到极限承载力Fu时，α也可被作为结构稳定性的安全系数Kα。在结果后处理过程中，分别取各阶段下有限元模型中筒身上的关键点P1、P2（如图2）的位移，将其换算为大圆筒筒身的转角，通过加载系数-筒身转角之间的关系，最终计算得出Kα。

2.4结果分析

综上所述，分别计算得到在不同施工阶段下，大圆筒围堰结构的稳定安全系数Kα以及结构的最大位移smax，结果如图3所示。

从图示中可以看出：

（1）在第一施工阶段（图3（a）），当大圆筒结构在波浪力和静水压力的共同作用下，其结构的安全系数 Kα=1.205>1，表明在该阶段结构安全；同时，从结构的位移云图中能够看出，在该阶段结构的最大位移出现在筒顶最右上角位置处，其最大位移smax=0.176m，为小变形，对结构的整体稳定性无影响；

（2）在第二施工阶段（图3（b）），当大圆筒结构在外堤土压力和静水压力的共同作用下，其结构的安全系数Kα=1.135>1，表明在该阶段结构安全；而在该阶段结构的最大位移出现在斜坡堤堤顶与大圆筒筒顶的接触位置处，其smax=0.271m；从数值上看，第二阶段较第一阶段而言，结构的稳定性有所降低，最不利位移值增大，但结构本身依旧安全，建议在该阶段采取临时内部支撑等相关措施，以杜绝安全隐患；

（3）在第三施工阶段（图3（c）），当大圆筒结构在内、外堤土压力和静水压力的共同作用下，其结构的安全系数Kα=1.395>1，表明在该阶段大圆筒围堰结构最为安全；同样，在该阶段结构的最大位移出现在斜坡堤堤顶与大圆筒筒顶的接触位置处，其smax=0.138m；从数值上看，第三阶段相比于前两个阶段而言，结构更加稳定，最不利位移在三个阶段中最小，表明最终方案能够满足结构安全稳定的使用要求。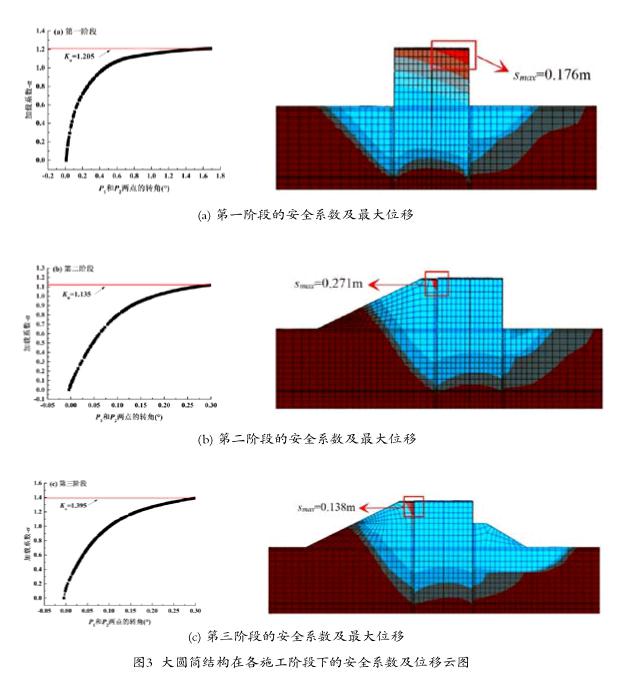

3.结论

本文以某人工岛工程为依托，基于有限元方法，对其中大圆筒围堰结构分别在三个重要施工阶段的稳定性进行数值模拟。通过建立不同施工阶段下大圆筒围堰结构与周围土体的“结构-地基相互作用”的有限元模型，利用加载系数法评估大圆筒及其土体的整体稳定性。最终分别计算得到在三个施工阶段下大圆筒围堰结构的稳定安全系数均大于1，表明结构安全；在三个施工阶段下，结构的稳定安全系数依次为：Kα（第三阶段）>Kα（第一阶段）>Kα（第二阶段），这说明在第三阶段结构最为稳定，而第二阶段则相比较而言要更加危险，建议在该阶段采取临时内部支撑等相关措施，以杜绝安全隐患；同时，在各施工阶段下结构的最大位移均较小，不会影响结构的整体安全；在第一阶段，smax出现在筒顶最右上角位置处，而在第二、三阶段，smax均出现在斜坡堤堤顶与大圆筒筒顶的接触位置处。本文的研究成果可为类似工程的设计提供一定的技术支撑。

参考文献：

[1]JTS 145-2-2013.海港水文规范[S].

[2]JTS 144-1-2010.港口工程荷载规范[S].[3]JTS 167-2-2009.重力式码头设计与施工规范[S].