蛋形断面的正常水深和临界水深的直接计算公式

卞晓卫，郑新桥，代述兵，简 跃,马玉蕾

(1.中国电建集团贵阳勘测设计研究院，贵州 贵阳 550081； 2.中国水电建设集团十五工程局有限公司， 陕西 西安 710068；3.大连理工大学建设工程学部，辽宁 大连 116024； 4.云南建工水利水电建设有限公司， 云南 昆明 650000)

蛋形断面的正常水深和临界水深的直接计算公式

卞晓卫1，郑新桥2，代述兵3，简 跃4,马玉蕾3

(1.中国电建集团贵阳勘测设计研究院，贵州 贵阳 550081； 2.中国水电建设集团十五工程局有限公司， 陕西 西安 710068；3.大连理工大学建设工程学部，辽宁 大连 116024； 4.云南建工水利水电建设有限公司， 云南 昆明 650000)

蛋形断面的正常水深和临界水深的计算公式为分段超越方程，无法直接求解。通过数学变换对正常水深和临界水深公式化简，最终得到充满度x和无量纲正常水深参数H、无量纲临界水深参数P之间的关系，利用1stopt软件基于遗传算法编程对给定非线性函数模型进行参数优化拟合建立蛋形断面正常水深和临界水深的显示计算公式。经过误差分析及实例计算，表明在较大工程常用范围内，蛋形断面正常水深、临界水深的最大相对误差分别仅为0.3691%、-0.0726%。与现有公式比较直接计算公式适用范围扩大，精度更高，形式较为简捷。研究成果可为渠道工程设计和运行管理提供可靠的理论依据和有益参考。

蛋形断面；正常水深；临界水深；1stopt软件；显示计算公式

蛋形断面是由底拱半径0.5 r，侧拱半径3 r，顶拱半径r的四段圆弧分别各自相切组成。蛋形断面在城市给排水工程中应用较多，在输水工程中亦有应用，其适用于过水流量变幅较大的工程，小流量工况比圆形断面流速更大，因而具有更好的排沙冲淤效果，且蛋形断面外形与压力曲线较为接近，力学条件好，能很好地用于地质条件差围岩压力较大的工程，另外其竖向高度比横向宽度大，因而其比圆形断面更便于人工入洞维修。

李若冰[1]对上小下大六圆弧蛋形断面的临界水深进行了深入研究；武周虎[2]给出了蛋形断面正常水深和临界水深误差较大的分段计算公式，且忽略掉了底拱部分的计算式；李风玲[3]给出了上小下大蛋形断面正常水深的近似计算方法；滕凯[4-6]对蛋形断面正常水深、临界水深及其水面线均进行了研究，但其适用范围偏小，误差较大；BijankhanM[7]得到误差达2%，且应用非常繁琐的蛋形断面均匀流水深的计算公式；RajkumarVRaikar[8]得到上小下大六圆弧蛋形断面正常水深和临界水深精度很高，但适用范围稍小的直接计算公式；张新燕、吕宏兴[9-10]对U型渠道和无压圆形隧洞的正常水深用软件模拟的方法进行了研究，得到了较好的结果。

蛋形断面的正常水深和临界水深计算公式均为复杂的高次隐函数，且蛋形的几何特征决定其计算需分段计算，因而利用传统的试算法和图解法等根本无法满足工程需要，本文利用数学变换，简化了正常水深和临界水深计算过程得到了充盈度x与无量纲正常水深H、无量纲临界水深P之间的数学表达式，利用1stopt软件，基于遗传算法对给定的非线性函数模型进行编程拟合，得到了精度较高且将分段函数统一表达的计算结果，是目前所有计算结果中最优的显式计算公式。

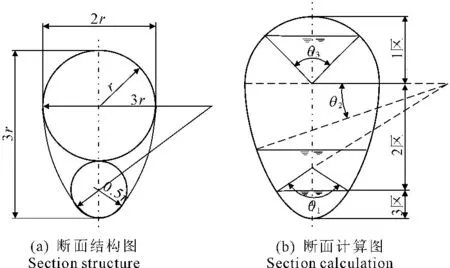
图1 蛋形过水断面示意图

Fig.1Egg-shapedflowsection

1 蛋形断面几何参数

(1)

(2)

(3)

2 正常水深显式计算公式

正常水深计算公式：

(4)

式中，Q为蛋形断面流量(m3·s-1)；A为过水断面面积(m2)；χ为湿周(m)；i为隧洞底坡降；n为隧洞内壁粗糙系数。

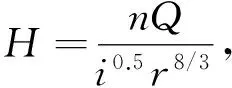
当0≤x<1/15时，将式(1)中过水断面面积A和湿周χ代入式(4)中可整理得到：

H=

(5)

当1/15≤x<2/3时，将式(2)中过水断面面积A和湿周χ代入式(4)中可整理得到：

(6)

当2/3≤x≤1时，将式(3)中过水断面面积A和湿周χ代入式(4)中可整理得到：

H=

(7)

理论上来说x∈[0,1]，但在实际工程中，小流量时x太小，则实际意义不大，大流量时避免明满流过度且为了便于计算，x取值也未取得太大，以往文献计算范围取x∈[0.04,0.83]，本文取比以前研究结果更大的区间进行计算x∈[0.03,0.9]，相应H∈[0.00521,3.3179]。

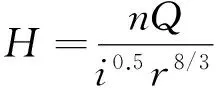
x=

(8)

将求得的充盈度x代入式(9)可求得正常水深h：

h=3rx

(9)

3 临界水深显式计算公式

临界流所应满足的基本方程为：

(10)

式中，α为流速不均匀系数，一般取1；Q为蛋形断面流量(m3·s-1)；g为重力加速度，取9.8 m·s-2；Ak为临界水深时对应的过水断面面积(m2)；Bk为临界水深时的水面宽度(m)。

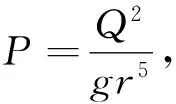
当0≤x<1/15时，将式(1)中过水断面面积A、水面宽度B代入式(10)中可整理得到：

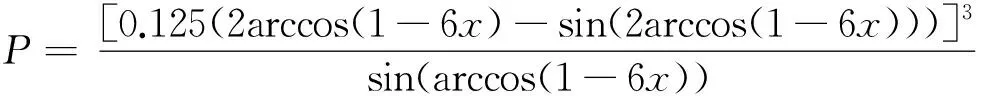
(11)

当1/15≤x<2/3时，将式(2)中过水断面面积A、水面宽度B代入式(10)中可整理得到：

(12)

当2/3≤x≤1时，将式(3)中过水断面面积A、水面宽度B代入式(10)中可整理得到：

(13)

理论上来说x∈[0,1]，但在实际工程中，小流量时x太小，则实际意义不大，大流量时避免明满流过度且为了便于计算，x取值也未取得太大，以往文献计算范围取x∈[0.05,0.80],本文取比以前研究结果更大的区间进行计算x∈[0.03,0.9]，相应P∈[7.498×10-5，55.613]。

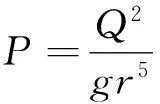
(14)

将求得的充盈度x代入下式可求得临界水深h：

h=3rx

(15)

4 误差分析及公式比较

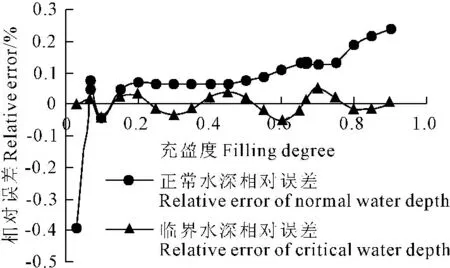
图2 相对误差分布

Fig.2Relativeerrordistribution

如下为目前关于蛋形断面正常水深、临界水深的计算公式统计表：

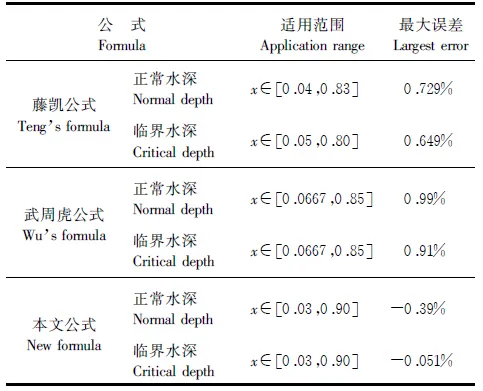
表1 不同公式比较

本文公式与以往正常水深、临界水深公式相比而言，适用范围均更大，达到x∈[0.03,0.90]，精度均更高，正常水深最大误差仅-0.39%，临界水深最大误差仅为-0.051%，且将分段函数的表达形式统一到一个计算表达式中来，计算更为便捷，具有较大的优势。

5 应用举例

某输水涵管为蛋形断面,上半圆半径r=0.5m,涵管底坡度i=0.0024,粗糙系数n=0.014,流量Q=1.4m·s-1，求均匀流正常水深和临界水深。

解：正常水深：

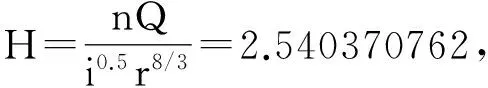
临界水深：

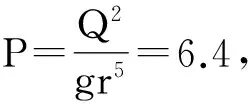
6 结 论

由于蛋形断面正常水深和临界水深公式均为无法直接求解的超越方程，且由几段相切的圆弧连接而成，因而以前的研究成果均是繁琐的分段函数、适用范围小且误差大，本文通过对方程代换变形得到了一个隐函数关系，通过给定充盈度x的取值区间得到了对应的无量纲正常水深参数H和无量纲临界水深参数P的取值范围，而后利用1stopt软件基于遗传算法编程对给定的非线性模型进行优化拟合得到最优参数，建立起蛋形断面的正常水深和临界水深的直接计算公式。通过误差分析及实例计算表明：

1) 本文所建立的直接计算公式克服了以前成果的缺点，得到了非分段函数的统一表达关系，避免分段函数需要判断分界点的不便，同时也避免了试算法，图解法的繁琐，并扩大了适用范围，充盈度取值范围扩大到x∈[0.03,0.9]，延展了取值范围的上限和下限，使公式具有更好的通用性。

2) 公式物理概念明确，计算简捷，计算精度高。所得正常水深、临界水深计算公式误差分别为-0.39%，-0.051%，具有较高精度，比以往任何公式的精度均更为精确，为工程设计和运行管理提供保证。

3) 本文利用1stopt软件基于遗传算法编程对给定的非线性函数模型进行优化拟合，所得结果的相关系数可达到0.9999999以上，所得结果拟合精度很高，拟合效果好，是一种求解非线性拟合的好方法，也为水力学中众多非线性问题开辟了一条新途径。

[1] 李若冰，张志昌.明渠六圆弧蛋形断面临界水深和收缩断面水深的计算[J].武汉大学学报(工学版)，2012,45(4):463-467.

[2] 武周虎.蛋形断面明渠正常水深和临界水深的简化算法[J].人民长江，2014,45(4):73-76.

[3] 李风玲，文 辉，涂宁宇.蛋形断面管道正常水深近似算法[J].人民长江，2008,39(18):77-78.

[4] 滕 凯.蛋形断面隧洞正常水深的简易算法[J].长江科学院院报，2013,30(12)：39-42.

[5] 滕 凯.蛋形断面隧洞临界水深的简易算法[J].水利水电科技进展，2013,33(6)：33-39.

[6] 滕 凯.断面无压隧洞水面线解析算法[J].水利水电科技进展，2014,34(2)：64-67.

[7] Bijankhan M, Kouchakzadeh S. Egg-shaped cross section: Uniform flow direct solution and stability identification[J]. Flow Measurement and Instrumentation, 2011,22:511-516.

[8] Rajkumar V Raikar, M S Shiva Reddy, G K Vishwanadh. Normal and critical depth computations for egg-shaped conduit sections[J]. Flow Measurement and Instrumentation, 2010,21:367-372.

[9] 张新燕，吕宏兴，朱德兰.U形渠道正常水深的直接水力计算公式[J].农业工程学报，2013,29(14):115-119.

[10] 张新燕，吕宏兴.无压圆形隧洞正常水深直接算法[J].水力发电学报，2014,33(1):127-131.

The explicit calculation formula of normal and critical water depth for egg-shaped section

BIAN Xiao-wei1， ZHENG Xin-qiao2， DAI Shu-bing3， JIAN Yue4， MA Yu-lei3

(1.PowerChinaGuiyangEngineeringCorporationLimited，Guiyang,Guizhou550811，China；2.SinohydroCorporationEngineeringBureau15Co.,Ltd.,Xi'an,Shaanxi710068,China;3.FacultyofInfrastructureEngineering,DalianUniversityofTechlonogy,Dalian,Liaoning116024,China;4.YunnanJiangongWaterResourceandHydroelectricConstructionCo.,Ltd.,Kunming,Yunnan650000,China)

The calculating formulas of normal and critical water depth for egg-shaped section are sectional transcendental equations, which can't be solved directly. In this article, the normal and critical depth formula is simplified by mathematical deformation, and then the relation of filling degreexwith nondimensional normal water depthHand nondimensional critical depthPis gotten. The 1stopt software is adopted to optimize and fit the established nonlinear model parameters based on genetic algorithm and set up the explicit calculation formula of normal and critical water depth for egg-shaped section. The error analysis and example calculation show that, within the large range of common project application, the largest relative errors of normal and critical water depth for egg-shaped section are just 0.3691% and -0.0726%, relatively. Compared with the existing formulas, the explicit formula is characterized by a larger application range, a higher precision and a more convenient calculation. The proposed formula will provide a theoretical basis and useful reference for project design, operation and management.

egg-shaped section; normal water depth; critical water depth;1stopt software; explicit calculation formula

1000-7601(2017)02-0191-04

10.7606/j.issn.1000-7601.2017.02.31

2015-12-18作者简介：卞晓卫，男，工程师，主要从事大坝安全监测工作。

简 跃，男，主要从事水利水电、房屋建筑施工工作。

TV131.4

A