不同喷射工况下的GDI喷雾模拟标定研究
秦征骁, 许敏, 尹鹏
(上海交通大学机械与动力工程学院汽车电子控制技术国家工程实验室, 上海 200240)
不同喷射工况下的GDI喷雾模拟标定研究
秦征骁, 许敏, 尹鹏
(上海交通大学机械与动力工程学院汽车电子控制技术国家工程实验室, 上海 200240)
准确模拟喷雾是提高缸内模拟准确性的关键,为了使模拟喷雾与试验喷雾更加一致,需要根据试验喷雾贯穿距及粒径对模拟喷雾进行标定。使用AVL FIRE软件建立定容弹及喷雾数值模型,对处于不同喷射工况(喷射压力、环境压力、油温)下的喷雾进行数值模拟,根据试验喷雾的贯穿距及喷嘴下方30 mm平面处SMD对模拟喷雾进行标定,并对不同喷射工况的标定参数选择进行探讨。结果表明:为了同时满足贯穿距和粒径的标定要求,需要根据工况参数对标定参数进行调整;对于本研究中的GDI喷油器,喷射压力10 MPa时使用KH-RT模型的模拟结果与试验值匹配较好,5 MPa时使用Huh-Gosman模型匹配更好;在喷射压力、环境压力和环境温度相同的条件下,高油温和低油温工况可以用同一套参数满足标定要求。
燃油喷雾; 标定; 数学模型
对于GDI发动机来说,准确模拟喷雾是模拟缸内油气混合的关键。目前已有多种模拟喷雾场的方法,其中离散液滴模型(DDM)由于其计算量小的特点,在工程上应用比较广泛。但是DDM方法的主要缺点是模拟结果依赖于模型的选择及模型参数的设置,应用不同的模型或参数,雾化质量和形态都可能有很大区别。因此需要根据喷雾试验的结果来对模拟结果进行修正,即喷雾标定[1]。破碎过程对于喷雾发展起着至关重要的作用,所以破碎模型是主要的标定模型。
已经有许多研究者应用DDM方法来模拟喷雾:一是在已知喷嘴内部结构的情况下,先进行孔内计算获得出口处流体的速度及湍流信息,然后以此作为输入计算孔外喷雾[2-3];二是直接将喷嘴出口液体设置成团块或粒径大小为某种分布的液滴群[4-9]。目前的有关喷雾模拟的文献主要集中于对新的喷雾模型的评估,开发新的喷雾模拟方法,以及应用数值模拟方法对喷雾现象或缸内油气混合现象进行研究等等,较少对喷雾标定过程进行探讨。事实上喷雾的标定过程会对喷雾模拟的准确性有非常重要的影响。耿超等使用Converge软件研究了KH-RT模型参数以及网格划分方法对喷雾模拟准确性的影响。邵利民等对高压共轨柴油喷雾进行了试验以及数值模拟,研究了KH-RT模型中的参数C2,C4在不同工况下的变化,发现C2对贯穿距影响较强且与环境压力密切相关,C4对贯穿距影响较弱。M. Costa等利用自动优化软件ModeFrontier,以试验与仿真贯穿距之间的误差为目标,对不同喷射压力及喷油脉宽下的喷雾模拟参数进行标定,并应用这些标定参数进行发动机性能计算。
本研究针对一款GDI发动机的喷油器,在不同喷射工况下进行喷雾定容弹试验及数值模拟,探究了不同喷射工况下的(包括喷射压力、环境压力、油温)喷雾模拟标定过程。
1 喷雾试验
本研究中使用的是GDI 6孔喷油器,喷油器下方50 mm处的落点见图1,为对称分布,1,6孔孔径为0.2 mm,2,5孔孔径为0.21 mm,3,4孔孔径为0.19 mm。喷雾试验及模拟中使用的燃油均为正庚烷。
1.1 白光测试
白光测试可以获得喷雾从喷射开始到喷射后期的喷雾图像,对图像处理可以得到喷雾的贯穿距、锥角和轮廓信息。白光测试的设备系统见图2。6 孔GDI喷油器安装在压力容器的顶部,可以通过高压氮气瓶和真空泵来调节容器内部的压力,并且燃油温度与环境温度也是可控的。CCD相机和瞬态白光灯通过容器侧壁上的石英玻璃来捕捉喷雾图像,PTU实现对整个试验过程的控制。
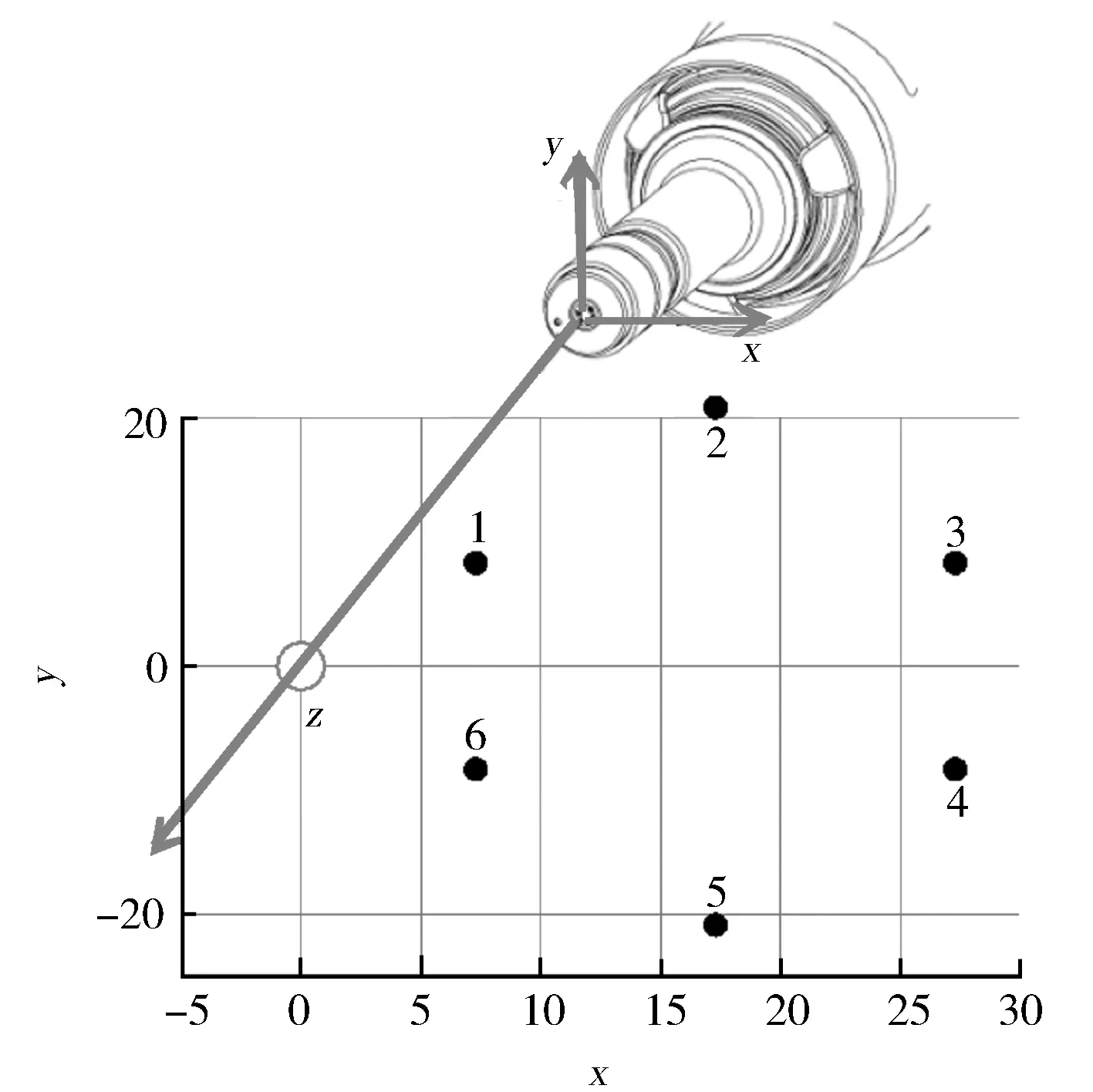
图1 喷油器50 mm下方落点分布
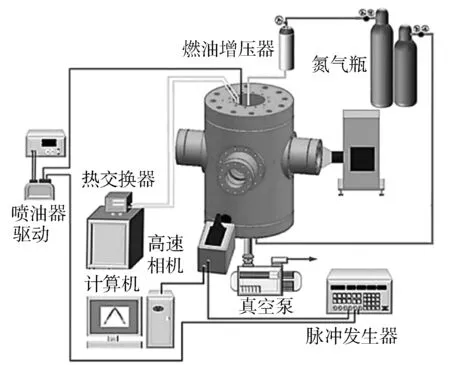
图2 白光测试设备
1.2 PDI测试
PDI测试可以获得喷雾的粒径分布,从而可以计算索特直径。PDI测试系统见图3。喷油器安装在压力容器顶端, 喷射压力、容器内部压力、容器温度和环境温度的控制与白光测试时一致。PDI 激光发射器发射的4束相干光从容器一侧光窗穿过并定位至测试空间位置点,PDI 信号接收器则从与入射光呈 150°夹角的另一侧光窗接收光信号。通过三坐标滑台可同时移动激光发射器和信号接收器,测试不同空间位置点的粒径。测试过程中采用多通道信号发生器来控制激光发射器、信号接收器和喷油器的同步。
1.3 工况点
为了使喷雾测试结果更加符合实际应用,按照相应的GDI发动机在不同状态下喷油时刻的工况来选取工况点,并能够体现不同喷射压力、环境压力和燃油温度下的喷雾变化。工况点选择见表1。
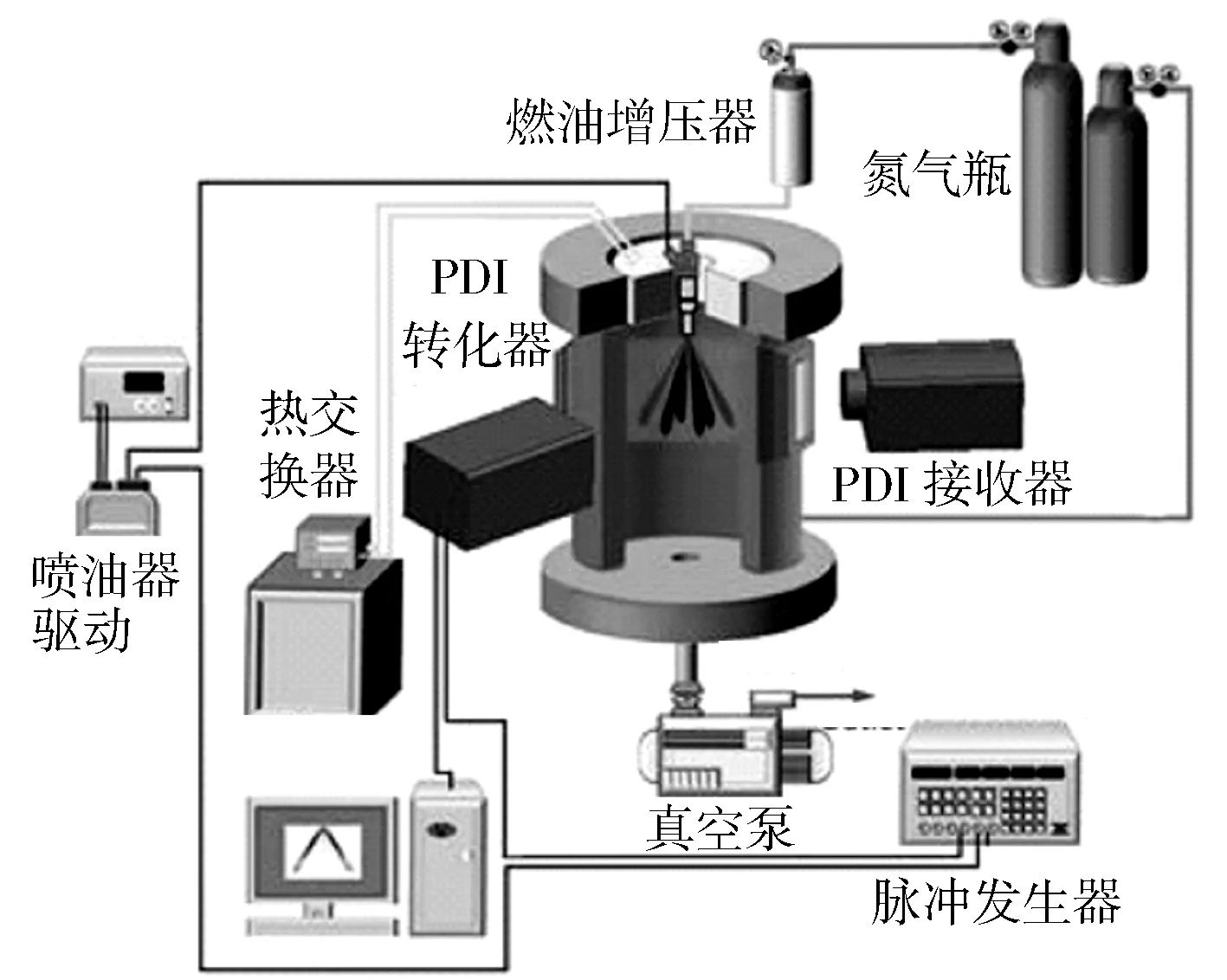
图3 PDI测试设备

序号喷射压力/MPa背压/kPa燃油温度/℃环境温度/℃110402530210100253031025025304102507530551002530
2 喷雾模拟
本研究使用AVL Fire进行喷雾模拟,喷嘴出口液滴设为Rosin-Rammler分布,模拟过程涉及的模型有液滴破碎模型(KH-RT,Huh-Gosman)、液滴碰撞模型(Schmidt-O’Rouke)、液滴蒸发模型(Dukowicz)、液滴湍流扩散模型(O’Rouke)。其中破碎模型是主要的标定模型。
2.1 网格设置
采用Fire软件的Topology工具建立六面体网格,根据试验获得的喷雾大小范围确定定容弹网格为直径80 mm,高度120 mm的圆柱体。

图4 定容弹网格
DDM方法的求解特点决定了其具有一定的网格依赖性。该方法将液滴和空气分别作为离散相和连续相进行处理,通过对两相交替求解实现喷雾的模拟。在这一过程中,网格需要足够小来保证气相求解的准确性,同时网格又不能太小,因为如果网格小于离散液滴大小则会影响液相求解。综合考虑计算成本及精度,选择网格大小为1 mm,并在后续进行缸内计算时采用同样大小网格进行计算,保证定容弹内喷雾与缸内喷雾模拟的一致性。图4为定容弹网格示意图。
2.2 Rosin-Rammler分布
由于出口处的喷雾破碎现象非常复杂,并且液滴密度较高,采用一般的光学手段不能很好地观察到喷嘴出口处的破碎现象。为了简化问题,一般假设液滴按照一定分布从喷嘴喷出,比较常用的是Rosin-Rammler分布,其公式如下:
(1)
式中:r为液滴粒径;F为粒径小于r的液滴在所有液滴中所占的体积百分比,其值为0~1;参数a是与粒径分布SMD有关的量,而q代表分布的宽度。图5示出分布参数a与q取值不同时的分布变化。参数a越大,则大粒径液滴在所有液滴中的占比越大;参数q越大,整个分布中的液滴粒径越集中,偏大和偏小的液滴在所有液滴中的占比均较小。通过以上分析,能够获得分布参数变化对出口液滴分布的影响规律,但是分布规律对于喷雾贯穿距和SMD的影响还需要通过参数敏感度分析来建立。

图5 分布参数a和q取值不同时的分布变化
2.3 KH-RT破碎模型
破碎模型是喷雾模拟中的重要一环,模型及其参数的选择会对喷雾模拟有重要影响。在KH-RT模型中,气体与液滴之间的气动作用形成的KH波的不稳定性增长决定初次破碎过程;空气阻力引起高速运动油滴发生变形,形成另一种不稳定波——RT波,在RT波的作用下液滴发生二次破碎。
KH波:破碎子液滴的大小由表面不稳定波的最大增长率决定。母液滴的半径变化率为
(2)
(3)
式中:τa为液滴破碎时间;系数C2用来修正特征破碎时间;rstable是生成的子液滴半径,其与不稳定波的最大波长Λ成比例:
(4)
比例参数C1常取值为0.61,计算中较少调整。波长Λ以及增长率Ω依赖于液滴所处位置的流体属性,表达式如下:
(5)
(6)
RT波:RT 不稳定波的振幅大于变形油滴的厚度时,液滴即将发生分裂,破碎受ΛRT和ΩRT控制,其表达式如下:
(7)
(8)
(9)
式中:KRT为波数,gt为油滴运动方向的加速度,C4为模型可调参数。
在KH-RT模型中,用来修正破碎KH波破碎时间的参数C2为主要标定参数。C2增大时,液滴破碎时间减小,从而使得相同时间内破碎程度增加,破碎后的液滴直径变小,在宏观上则表现为贯穿距减小,30 mm处的SMD减小。
2.4 Huh-Gosman破碎模型
Huh-Gosman模型的基本思想:射流内部的湍流扰动和气体的惯性力是导致液体分裂雾化的动因,即假设喷雾的破碎是由喷嘴射流的湍流扰动和气动力引起的,而这种湍流扰动可以用湍流长度尺度Lt和时间尺度τt来描述,这两个尺度的定义如下:
(10)
(11)
(12)
(13)
破碎长度尺度LA可以由湍流长度尺度Lt计算得来,破碎时间尺度τA则通过湍流以及空气动力时间尺度的组合得来,其中空气动力时间尺度C4是主要标定参数。C4减小时,造成破碎时间尺度τA减小,从而相同时间内破碎程度增加,从宏观上表现为贯穿距减小,30 mm平面处SMD减小。
(14)
(15)
3 喷雾标定
喷雾是液滴破碎和碰撞的综合过程,虽然数值模拟中使用到的模型均是依靠物理模型推导得到的,但是其中依然有许多需要根据试验数据调整的参数,如果没有标定的过程,模拟结果难以体现实际喷雾的情况。由于KH-RT模型是比较常用的模型,因此先选择该模型对选定的工况点进行喷雾模拟。将模拟喷雾的贯穿距与喷嘴下方30 mm平面处的SMD值(以下简称SMD)同试验值进行对比,调整模拟参数置使试验值和模拟值有较好的一致性。
3.1 参数敏感度分析
速度范围可以由伯努利方程得到,但是由于流量系数Cd无法测量,因此出口速度也作为标定量,在方程计算的范围内进行调整。
(16)
对标定过程涉及的参数进行敏感度分析,包括出口速度、Rosin-Rammler分布参数a和q、KH-RT模型参数C2。图6示出出口速度对模拟喷雾贯穿距和SMD的影响。由图6可看出,喷射前期液滴比较密集,此时液滴运动主要受初始速度影响,因而可以看到在喷射初期,喷雾出口速度越大,其贯穿距也越大;但是进入喷射后期,速度大的液滴受到的空气阻力和破碎强度也越大,因而出口速度越大的液滴,其SMD越小。
图7示出分布参数对模拟喷雾的贯穿距和SMD的影响。由图7可以看出,a参数越大,贯穿距和SMD也越大,这是因为分布参数a越大,出口液滴群中粒径较大的液滴所占比重也越大,因此,贯穿距和SMD也增大。而参数q影响分布中液滴大小的集中度,从图7来看,q增大,贯穿距和SMD均增大。


图6 出口速度对贯穿距与SMD的影响
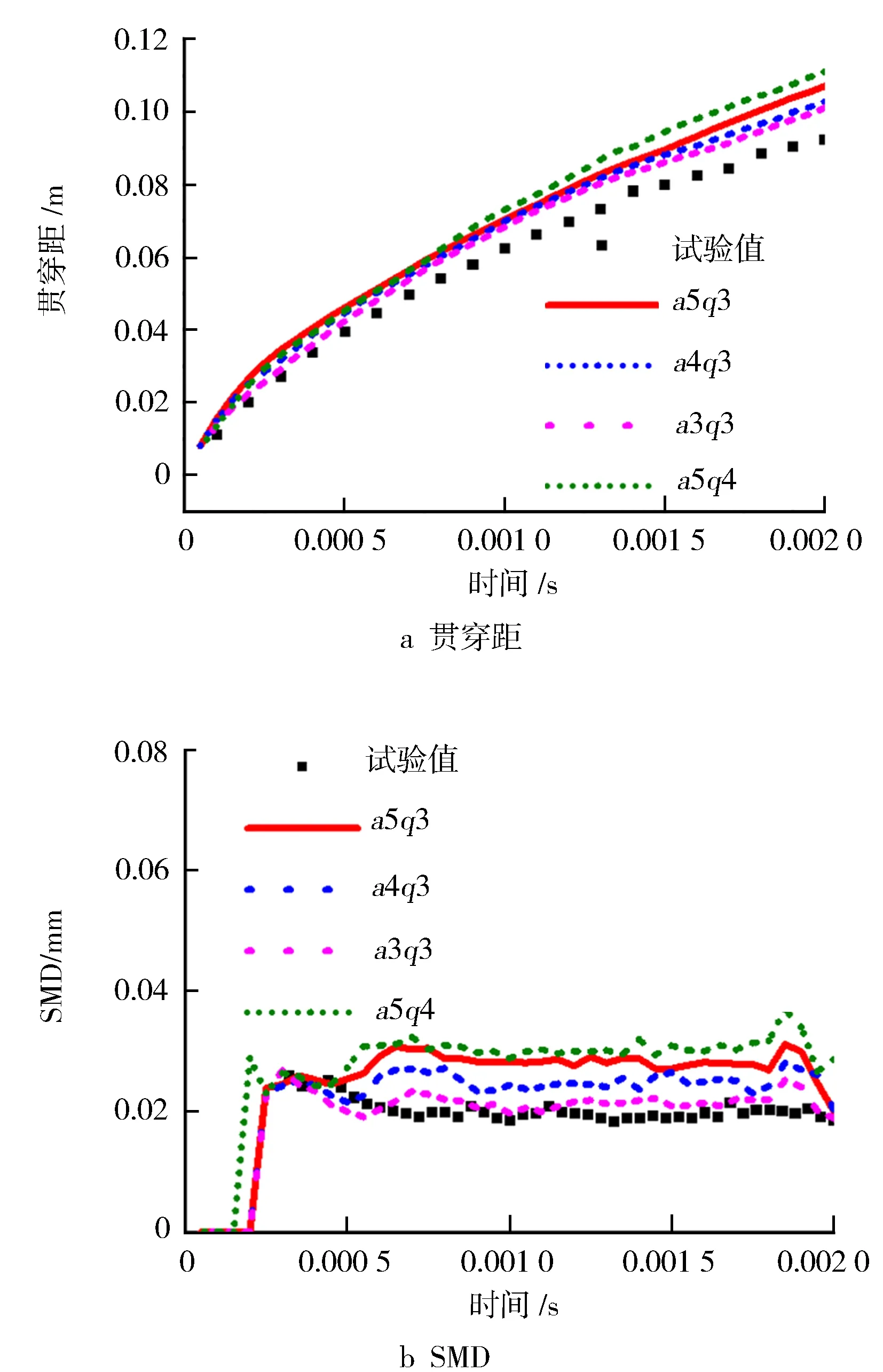
图7 分布参数对贯穿距与SMD的影响
图8示出KH-RT模型参数C2取值不同时对贯穿距和SMD的影响。C2是调整液滴破碎时间的参数,增大C2即增大破碎时间,从而破碎强度会减小,因此贯穿距和SMD都会增大。
通过敏感度分析,建立了标定参数变化与模拟喷雾贯穿距和SMD的变化之间的联系,为喷雾标定中的参数调整提供指导。由喷雾特性可知,在喷雾发展初期,也就是在破碎长度内,喷雾的发展主要由出口液滴的速度所决定。因此先根据前期的试验喷雾贯穿距调整初始速度,然后根据30 mm平面处的SMD调整出口的液滴粒径分布,最后对喷雾破碎模型参数进行调整。图9示出本研究在对喷雾进行标定时的流程。

图8 KH-RT模型参数C2对贯穿距与SMD的影响

图9 喷雾标定参数调整流程
3.2 喷雾标定
图10至图12分别示出工况1、2、3经过标定之后的结果,其喷射压力均为10 MPa,环境压力分别为40 kPa,100 kPa和250 kPa,环境温度为30 ℃,油温为25 ℃。经过喷雾标定,模拟喷雾的贯穿距与SMD同试验值能够很好地吻合,但是还需对比喷雾宏观形态及落点分布进行验证。以工况2试验与模拟的喷雾进行验证,图13示出试验(上)与模拟(下)喷雾的宏观形态对比,图14示出试验(右)与模拟(左)的喷雾落点分布对比。经过形态和落点对比,可以认为模拟喷雾与试验喷雾有比较好的一致性。

图10 工况1标定后喷雾贯穿距与SMD对比

图11 工况2标定后喷雾贯穿距与SMD对比

图12 工况3标定后喷雾贯穿距与SMD对比

图13 工况2试验(上)与模拟(下)喷雾的宏观形态对比

图14 工况2试验(右)与模拟(左)喷雾的落点分布对比
对于喷射压力为10 MPa,环境压力不同的3个工况,上文建立的喷雾计算模型能够获得与试验结
果吻合较好的模拟结果。但是在模拟喷射压力为5 MPa的喷雾时,即使对参数进行不同组合的调整,也不能使模拟得到的贯穿距和SMD同试验值吻合。并且发现模拟喷雾贯穿距总是在喷雾发展后期要大于试验贯穿距。因此使用Huh-Gosman模型代替KH-RT模型来模拟喷射压力为5 MPa的喷雾,对Huh-Gosman模型中代表气动破碎时间尺度的参数C4进行调整,获得与试验值比较相符的喷雾结果(见图15)。工况5的喷雾宏观形态和落点分布对比见图16和图17。

图15 使用KH-RT及HuhGosman模型标定后的喷雾贯穿距与SMD对比

图16 工况5试验(上)与模拟(下)喷雾的宏观形态对比

图17 工况5试验(右)与模拟(左)喷雾的落点分布对比
实际喷雾的雾化过程可分为初次雾化和二次雾化,初次雾化是指高压液体从喷嘴射出后,发生分裂,在靠近喷嘴处形成大小形状各不相同的液体微团,二次雾化则是指这些液体微团发生再一次雾化形成更小的液滴[10]。而在本研究使用的喷雾模拟方法中,并不区分初次破碎和二次破碎,认为射流以液滴群的形式从喷嘴进入计算域,之后用同一个破碎模型来考虑破碎问题。由图15可看出,在喷射压力为5 MPa情况下,使用KH-RT模型的模拟喷雾初期与试验值吻合,但后期偏差较大,说明在此工况下,模拟喷雾的二次破碎强度不够,导致喷雾后期的贯穿距要比试验值更大。文献[4]在比较不同破碎模型的准确性时也报告了这一现象,并提到二次破碎阶段的粒径与初次破碎阶段的粒径之间的变化不明显的情况。这进一步说明,在喷雾后期模拟喷雾贯穿距与试验贯穿距相比偏大是因为在该工况下KH-RT模型在二次破碎阶段的破碎强度不够。如图16所示,Huh-Gosman模型能够很好地捕捉到喷射压力为5 MPa下的初次破碎和二次破碎过程,因而在这一工况下采用Huh-Gosman破碎模型进行喷雾模拟更加合理。
图18示出工况3,4的试验贯穿距与SMD。从图18可以发现,环境温度与燃油温度的影响主要在于喷雾后期,喷雾前期的贯穿距主要受喷射压力及环境压力的影响。基于这一现象,沿用工况3(相同

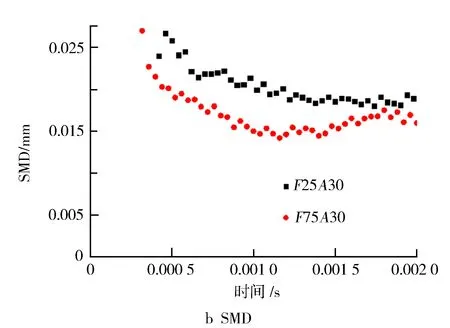
图18 工况3,4试验贯穿距与SMD对比结果
喷射压力、喷射背压)的破碎模型参数,得到的标定结果见图19,模拟值与试验值基本吻合。最后得到不同工况下经过标定的参数(见表2)。
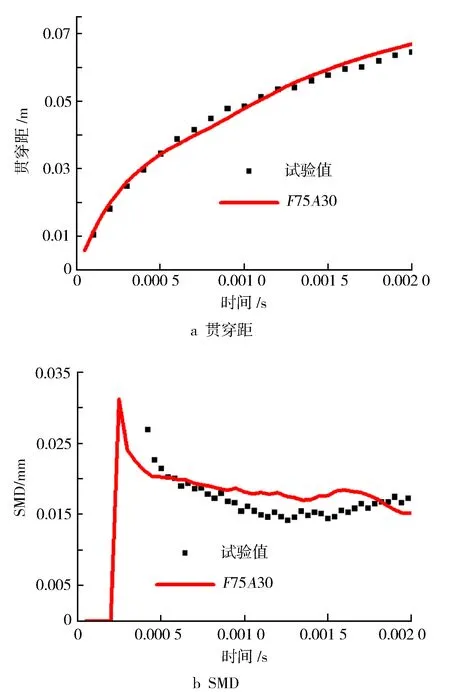
图19 工况4标定后喷雾贯穿距与SMD对比

工况VaqKH⁃RTC211502.431215043531506324415063245851485(C4)
其中工况5的破碎模型参数为Huh-Gosman模型中的参数C4,取值为5。在后续进行GDI发动机缸内油气混合计算时,可以按照发动机所处的工况,选取对应的喷雾标定参数来设置喷雾模块,提高缸内油气混合模拟的准确性。
4 结论
a) 为了同时满足贯穿距和粒径的标定要求,需要根据工况参数对喷雾模拟设置进行调整,从而获得在不同工况下喷雾模拟参数的取值,以便在缸内油气混合计算中应用;
b) 喷射压力10 MPa时使用KH-RT模型的模拟结果与试验值匹配较好,5 MPa时使用Huh-Gosman模型模拟结果更好;
c) 在喷射压力、环境压力和环境温度相同的条件下,高油温和低油温工况可以用同一套参数满足标定要求。
[1] 李相超.先进直喷汽油机喷嘴选型与匹配技术研究[D].上海:上海交通大学,2012.
[2] 刘芬.GDI 喷嘴内流及喷雾特性的研究[D].武汉:华中科技大学,2012.
[3] 朱斌.油醇混合燃料喷雾特性研究及喷嘴优化[D].上海:上海交通大学,2011.
[4] Li Z H,He B Q,Zhao H.Application of a hybrid breakup model for the spray simulation of a multi-hole injector used for a DISI gasoline engine[J].Applied Thermal Engineering,2014,65(1): 282-292.
[5] Malaguti S,Fontanesi S,Severi E.Numerical analysis of GDI engine cold-start at low ambient temperatures[C].SAE Paper 2010-01-2013.
[6] Yeoh E Y L,Davy M H.Numerical Study of the Effects of Droplet Size Distribution on Fuel Transport and Air-Fuel Mixing in a Gasoline Direct-Injection Engine[C].SAE Paper 2003-01-3100.
[7] Costa M,Iorio B,Sorge U,et al.Assessment of a numerical model for multi-hole gasoline sprays to be employed in the simulation of spark ignition GDI engines with a jet-guided combustion mode[C].SAE Paper 2009-01-1915.
[8] Rathinam B,Naithani U,Delahaye L,et al.Numerical Spray Modeling for Ultra Low Cost (ULC) Gasoline Engine[C].SAE Paper 2013-10-1606.
[9] 王燕军,王建昕,帅石金.GDI 汽油机喷雾模型的改进和数值模拟[J].清华大学学报(自然科学版),2002,42(8):1110-1112.
[10] 解茂昭.内燃机计算燃烧学[J].大连:大连理工大学出版社,2005.
[编辑: 袁晓燕]
GDI Spray Calibration under Different Injection Conditions
QIN Zhengxiao, XU Min, YIN Peng
(School of Mechanical Engineering, Shanghai Jiao Tong University, National Engineering Laboratory for AutomotiveElectronnic Control Technology, Shanghai 200240, China)
Simulating the in-cylinder spray correctly is the key step to improve the in-cylinder simulation. It is usually necessary to calibrate simulated spray according to measured spray penetration and droplet size in order to achieve the uniformity between the simulated spray and the test spray. The spray simulation under different conditions of injection pressure, ambient pressure and fuel temperature was carried out with the numerical model of constant volume bomb and spray established by AVL FIRE software. The simulated spray was calibrated according to the penetration of test spray and the SMD at the plane of 30 mm below the nozzle and the calibration parameters of different injection conditions were discussed. The results show that spray simulation parameters need to be adjusted under various conditions. The simulation results of KH-RT and Huh-Gosman breakup model are in good agreement with the experimental values when their respective injection pressure is 10 MPa and 5 MPa. Besides, the calibration parameters are little influenced by fuel temperature.
fuel spray; calibration; numerical model
2016-11-13;
2017-03-02
秦征骁(1991—),男,硕士,主要研究方向为汽油机缸内CFD计算;qzxelven@163.com。
10.3969/j.issn.1001-2222.2017.02.004
TK421.43
B
1001-2222(2017)02-0019-08

