引起速度场建场误差的几个关键环节
刘勇江
中石化江汉油田分公司物探研究院,湖北 武汉
引起速度场建场误差的几个关键环节
刘勇江
中石化江汉油田分公司物探研究院,湖北 武汉
地震成果由时间域转换到深度域,涉及速度建场和变速成图技术。随着水平井的广泛应用,对转深精度要求更高。特别在复杂山地探区,地震资料品质和地层速度在横向和纵向上变化比较剧烈,加之基准面计算方法不合理,导致转深的区域构造形态与深度预测精度往往很低,使得水平井的钻探设计和成本控制变得十分困难。通过在建场过程中对各个环节减小误差,进而提高整体速度场精度。对引起速度场建场误差的关键环节进行分析后认为,从基于表层模型的CMP (共中心点)基准面转换、模型迭代层速度计算、地震反射层约束速度场建立、两步法层速度误差校正方法入手,降低各个环节的误差,能够提高适用于盆边山地过渡带的速度场精度。
速度场建模,模型迭代层速度计算,两步法误差趋势面校正
Copyright © 2017 by author, Yangtze University and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
1.引言
涪陵地区地处四川盆地和盆边山地过渡地带,构造位置位于四川盆地川东南构造区川东高陡褶皱带,万县复向斜包鸾–焦石坝背斜带中的焦石坝背斜,构造呈北东向展布。境内地势以低山丘陵为主,横跨长江南北、纵贯乌江东西两岸。涪陵地区地震地质条件复杂,速度变化剧烈,传统速度场建场方法误差大,不能满足实际生产需求。在研究该地区表层结构、深层地质和速度资料特点的基础上,通过分析影响速度建场和变速成图精度的因素,从基于表层模型的速度谱CMP (共中心点)时间面到深度面的转换、模型迭代层速度计算、基于层位约束的两步法层速度误差趋势面构建等方法入手,建立了适用于复杂山地的高精度速度场建场技术。该技术在焦石坝地区的水平井钻井实践中,减少了钻探过程中井轨迹的调整次数,提高了水平井设计和钻探精度,降低了成本,取得了很好的效果,具有较高的生产应用价值。
2.高精度速度场建场思路
高精度速度场建立,实际上就是提高速度精度、消除速度误差。通过对焦石坝三维地震工区速度误差产生的原因分析,主要是在基准面转换、层速度计算、地震速度与测井速度差异、速度场校正方法等方面产生的误差。针对误差产生的特点,采取在建场过程中对各个环节进行误差校正的思路,通过降低每一环节的误差,使整体误差降低,进而提高速度场精度。具体方法为:采用基于表层模型的基准面转换技术,减小CMP基准面转换误差;采用模型迭代法计算层速度,用以减小直接使用Dix公式产生的误差;利用层约束速度建场技术减小层速度在纵横向空间上的误差;采用两步法误差趋势面校正技术减小井震之间的误差;利用钻探开发的时移性,用新的钻井信息对最终速度场进行局部误差校正,使速度场不断求精。高精度速度场建场流程如图1所示。
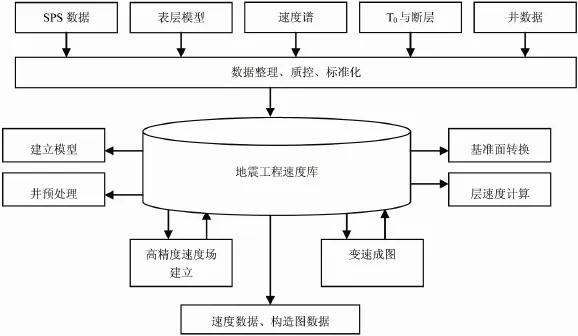
Figure 1.The flow chart of high precision velocity field图1.高精度速度场建场流程图
3.关键技术方法研究
3.1.基于表层模型的CMP基准面转换
在地震资料解释中,关键的一个环节是时深转换,目前时深转换选取的基准面均为速度分析基准面,即CMP面[1]。由于CMP面是速度谱的零线,是时间域的浮动面,是静校正量中的低频分量[2],不能简单地作为时间域转换的基准面,其大小受表层厚度、速度、基准面高程以及充填速度影响。传统时深转换方法大多忽略了CMP基准面转换对深度误差的影响,特别是在复杂山地地区,仅用替换速度和CMP时间量计算转换量,会造成与实际高程值的不符。图2为建立的水平模型,其中(a)为表层深度模型,(b)为(a)的时间模型,当中包含了CMP时间面。从图2(a)与图2(b)的对比中可以看出,若不考虑低降速带的速度和厚度,计算出来的CMP基准面高程与实际CMP基准面(地表面)高程之间误差为35 m,该误差势必会造成基准面转换时的速度误差,从而影响时深转换的精度。
采用基于表层模型的浮动基准面转换技术,考虑表层模型对速度的影响,可以提高基准面转换的精度,使速度更趋向真实。改进的CMP基准面高程的计算方法为:考虑静校正的替换计算,采用反替换(或称为反静校)来求取CMP基准面高程。
常规方法:


Figure 2.The sketch for calculating CMP reference surface elevation errors图2.计算CMP基准面高程误差示意图
改进方法:

式中:Hcmp1为常规方法计算得到的CMP基准面高程,m;Hd为固定基准面高程,m;Tcmp为CMP校正量,s;vr为替换速度,m/s;Hcmp2为改进方法计算得到的CMP基准面高程,m;Hg为高速顶(低速带底)高程,m;v0为低速度带速度,m/s。
从改进公式(式(2))中可以看出,考虑了替换速度、低降速层速度和厚度的影响,计算得到更为接近实际情况的CMP面高程。基于表层模型的速度谱基准面转换,是使时间域CMP基准面向深度域转换误差更小的有效方法。换算后的CMP直接转深面不仅受地表高程影响,也受高速层顶界面起伏影响,使得换算后的基准面与地表面并非完全一致,而采用基于表层模型的CMP转深面更贴近地表面(图3)。

Figure 3.The comparison between the surface, CMP in depth smooth based on surface model and direct in depth surface smooth图3.地表面、基于表层模型的CMP转深圆滑面、CMP直接转深面圆滑面对比
3.2.模型迭代层速度计算
常规速度建场中,通常采用Dix公式将均方根速度转换成层速度或平均速度。但Dix公式是在地下水平均匀层状介质、射线垂直入射的假设前提下建立起来的数学关系式。对于速度各向异性较强和速度出现倒转现象的地区是不适合的。采用模型迭代方法进行反演是解决层速度精度问题的有效途径之一[3]。模型迭代方法为:首先由Dix公式给出初始层速度模型;然后利用T0计算的谱点对应的倾角,通过射线追踪法求出反射波时距曲线,得到模拟速度谱;再用理论曲线对其进行拟合,求出理论叠加速度;最后将该速度与速度谱上的叠加速度进行比较,当误差小到合理精度时,即认为所给模型是正确的,输出所求的层速度值。该方法不受模型是水平层状介质和速度不能翻转的限制,计算精度要高于Dix公式。模型迭代流程如图4所示。

Figure 4.The flow chart of model iteration图4.模型迭代流程图
3.3.反射层位约束层速度场
由地质人员解释得到的T0图,转换为能够定井位的构造图,需要平均速度作为桥梁。平均速度的精度直接影响构造图的精度。对平均速度的直接编辑、平滑,会影响到各个目的层,导致当前目的层精度提高,其他目的层精度下降。为了解决该问题,引入地质反射层约束技术,原理是利用叠加速度和若干地质反射层,建立按 T0层位变化的层速度场(同时也可以按产状对地质分层进行细分小层),误差的校正均在约束的层速度场上进行,对分层内层速度进行编辑、平滑,既可以保证当前层速度的纵向和横向速度变化趋势,使层间速度更能代表实际速度的变化规律,又不影响其他层的速度变化,用该方法来提高速度场精度。图5~图7为间隔抽取的约束前、后的层速度对比图,可以看到,反射层约束前的层速度(图5)不能反映当前层速度的纵向和横向速度变化趋势,通过地震剖面解释的层位(图 6)约束后的层速度(图7)更能反映层速度沿层的变化规律。
3.4.两步法误差趋势面校正
速度误差产生的原因除了基准面转换、层速度计算等因素外,还有地震分辨率对速度谱影响产生的误差、岩性变化引起的误差、地震速度与井筒测量的速度间误差、追踪层位精度引起的误差、资料处理中速度陷阱等[4]。上述误差参杂在一起,反映到井点上也就是井点误差。以往对误差的校正主要采用数学插值网格化运算,以求出误差分布的趋势面,这与井的数量、分布均匀程度都有密切关系,其结果是在井点处精度较高,但其他部位容易引起变形扭曲,使得预测精度不高[5]。

Figure 5.The layer velocity profile before the reflector constraints图5.反射层约束前层速度剖面图
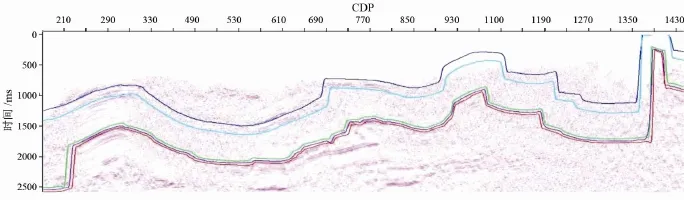
Figure 6.The horizon profile of seismic interpretation图6.地震解释层位剖面图

Figure 7.The layer velocity profile after the reflector constraints图7.反射层约束后层速度剖面图
通过研究认为,综合误差可以分解成规律误差和残余误差两部分。规律误差是与整体速度场相关的误差,为随时间、速度、深度等因素变化的函数,相对较平缓(图8)。残余误差是与具体位置相关的、局部的误差。两步法误差趋势面校正就是针对上述两种类型误差进行分别校正。该方法的优势是规律速度校正时不使用井数据,校正后基本保留了地震速度的变化趋势,能够较好地保持构造形态(图9)。

Figure 8.The comparison of well point error before and after the velocity correction图8.目的层规律速度校正前、后井点误差对比图

Figure 9.The distribution of residual error in the target layer corrected by two step method图9.目的层两步法校正后的剩余误差分布图
4.效果分析
利用上述方法在104口正钻井中进行应用,统计完钻的100口水平井,水平段共计152935.2 m,优质储层段钻遇率为85%,A靶点调整后的深度与实钻靶点深度误差小于20 m的占91.3%,水平井的入靶精度和穿行效率均较高,取得了较好的应用效果。
5.结语
笔者提出的引起速度场建场误差的几个关键环节,以实际勘探开发需求为驱动,改进了复杂山地地区传统建场方法和研究思路,通过实际应用,使速度场建场的精度得到了很大的提高。
基金项目
中国石油化工股份有限公司科研项目(ZKW4013002)。
References)
[1] 李杏莉, 王彦春.不同基准面上的速度场及时深转换[J].物探与化探, 2009, 33(1): 49-53.
[2] 苏勤, 吕彬, 田彦灿, 等.浮动面叠前深度偏移法在山前带复杂构造成像中的应用[J].新疆石油地质, 2009, 30(5): 560-562.
[3] 徐广民, 刘超颖, 王华忠.复杂构造速度反演方法研究[C]//中国石油学会, 中国地球物理学会.北海: 中国石油学会东部地区第十三次物探技术研讨会, 2005.
[4] 徐峰, 崔庆辉.复杂地区近地表对速度分析的影响[J].大庆石油地质与开发, 2010, 29(1): 124-128.
[5] 满益志, 王兴军, 张耀堂, 等.复杂逆掩构造及低幅度构造变速成图技术与应用[J].天然气工业, 2007, 27(s1): 211-214.
Correction
A Few Key Links Inducing the Errors in Velocity Field
Yongjiang Liu
Geophysical Exploration Research Institute, Jianghan Oilfield Company, SINOPEC, Wuhan Hubei

Received: Nov.1st, 2016; accepted: Jan.4th, 2017; published: Apr.15th, 2017
The seismic results were turned from time domain to the in depth domain, it involved the velocity field and the varying velocity mapping technique.With the wide application of the horizontal wells, counter rotating depth demanded a higher precision.Particularly in complex mountain exploration areas, changes of data quality and formation velocity on the horizontal and vertical directions were severe, combined with the unreasonable datum calculation method, the in depth tectonic shape and depth prediction precision were often low; it was very difficult for the design of the horizontal well drilling and its cost control.By building of the field for each link in the process of reducing measure error, the overall precision of velocity field is improved.In this paper, the velocity field building error in the key links is analyzed, it is considered that from the CMP datum transformation, the layer iteration speed calculation based on surface model, the building of seismic reflection velocity field, it is started from the two step interval velocity error correction method, the error of each link is reduced; it can improve the velocity accuracy for the basin edge and mountain transition zones.
Velocity Field Modeling, Model Iteration Layer Velocity Calculation, Two Step Error Trend Surface
刘勇江(1983-),男,硕士,工程师,现主要从事页岩气地球物理应用研究。

2016年11月1日;录用日期:2017年1月4日;发布日期:2017年4月15日
文章引用: 刘勇江.引起速度场建场误差的几个关键环节[J].石油天然气学报, 2017, 39(2): 36-43.https://doi.org/10.12677/jogt.2017.392015

