自适应显式互补滤波在六旋翼飞行器中的应用*

刘 洲， 单修洋， 谭 芳

(中南大学 机电工程学院，湖南 长沙 410083)

自适应显式互补滤波在六旋翼飞行器中的应用*

刘 洲， 单修洋， 谭 芳

(中南大学 机电工程学院，湖南 长沙 410083)

针对六旋翼飞行器的惯性传感器在测量过程中存在漂移的问题，提出了基于自适应显式互补滤波的姿态解算算法，并对该算法的原理和稳定性进行分析；搭建了六旋翼飞行器的实验测试装置，并进行机体的动、静态测试实验。在实验中，对自适应显式互补滤波算法、显式互补滤波算法以及陀螺仪传感器测量方法进行比较。实验结果表明：自适应显式互补滤波算法能够实现惯性传感器的解算姿态角误差收敛，且动态误差最小。

自适应显式互补滤波； 六旋翼飞行器； 姿态解算； 惯性传感器； 陀螺仪

0 引 言

六旋翼飞行器惯性测量单元IMU使用的是微机电系统(micro-electro-mechanical system,MEMS)类型传感器。该类型传感器中陀螺仪能够测量机体旋转角速度，且动态跟踪性能好。但由于测量角度是通过角速度积分得到，且陀螺仪本身存在漂移，随时间的积累，角度值存在很大误差。因此，需采用信息融合策略将多种传感器的数据进行处理，以提高姿态解算的精度。国内外学者提出了一系列的算法如卡尔曼滤波[1～3]、粒子滤波[4,5]和互补滤波[6,7]。经典互补滤波在频域角度对多个传感器数据进行融合，消除噪声干扰。该算法计算量小，相比粒子滤波不需要计算系统状态变量的概率密度[4,5]；相比卡尔曼滤波不需要计算噪声序列的方差矩阵[6]。Mahony提出了一种显式的非线性互补滤波(explicit complementary filtering，ECF)并应用于垂直起落飞行器中[8,9]；在ECF的基础上，许多学者对ECF中的增益进行在线调整[9～12]。本文针对陀螺仪存在漂移及六旋翼飞行器机体姿态变化剧烈(如杂技动作)时，加速度计修正滞后的问题，提出了自适应显式互补滤波算法(AECF)。该算法相比ECF可根据机体角速度实时动态调节补偿系数，从而加快速度计对陀螺仪的修正。实验结果表明：AECF融合算法能更好减少系统动态误差，满足六旋翼飞行器的姿态解算要求。

1 姿态解算原理

1.1 坐标系定义

六旋翼飞行器的姿态描述需要定义导航坐标系(n系)和机体坐标系(b系)。如图1所示，n系采用东北天的原则选择坐标轴(X，Y，Z)的正方向;b系的坐标轴为x，y，z。飞行器的姿态角度在n系中分别用横滚角φ、俯仰角θ和偏航角ψ描述。

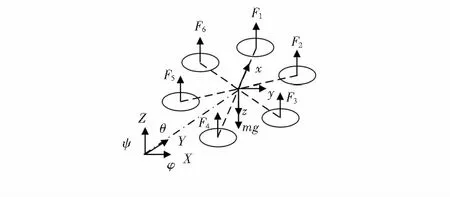
图1 六旋翼飞行器的坐标系

捷联惯性导航系统将惯性传感器直接固定在飞行器上，惯性传感器测得的数据基于b系，所以姿态解算结果的坐标需从b系转换到n系。转换过程如式(1)[13]

(1)

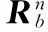
(2)

1.2 姿态更新

根据机体角速度与地理坐标下的姿态之间的关系[14]，姿态更新表达式如下

(3)

式中Ωb为测量的机体角速度。设固定在载体上的陀螺仪三轴输出角速度为ωb,则

(4)

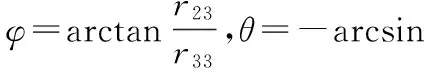
(5)

2 基于AECF的融合算法

自适应显式互补滤波姿态算法原理如图2所示。

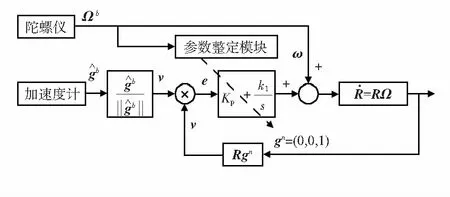
图2 六旋翼姿态解算算法框图

AECF的姿态观测状态方程如下

(6)

2.1AECF稳定性验证

根据系统误差定义Lyapunov函数V[13]为

(7)

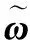
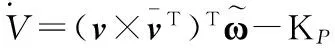
(8)

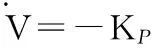
(9)

2.2 参数整定

图2中参数整定模块的KP，KI取值规则如下

(10)

式中 ωmax为陀螺仪的最大量程；ωc为陀螺仪的截止角速度(ωc<ωmax)；KP0为初始补偿系数；KP1为临界补偿系数。

KP0根据陀螺仪的ωc以及陀螺仪和加速度计动态响应特性进行选取。当机体角速度低于陀螺仪的截至频率ωc时，陀螺仪的测量不满足信号不失真的条件，所以，选择恒定的KP0。机体角速度越大，相应地提高KP使得加速度计更快地修正陀螺仪的偏差。然而，KP过大会导致高频滤波效果差，信号毛刺增加。当机体角速度超过陀螺仪的量程ωmax时，KP取最大值，即KP1。积分系数KI的加入可以消除陀螺仪漂移常值误差。为了保证实时性，选择KI为常值。文献[8]给出了SO(3)下ECF算法的相关理论证明，文献[10]和文献[14]给出了AECF算法中KP，KI的整定规则的证明。

3 实验测试

3.1 实验平台搭建

针对轴距为550mm的六旋翼飞行器搭建系统实验平台。选择意法公司生产的主频168MHz，STM32F427作为核心控制器,InvenSense公司的MPU6050传感器作为姿态的解算的硬件平台,实验平台如图3所示。

图3 六旋翼飞行器的实验平台

令陀螺仪输出信号的低通滤波器的截至频率ωc=100Hz，陀螺仪的输出量程为±1 000(°)/s，因此，ωmax=1 000(°)/s，更新周期为0.002 5s，取KP0=0.2，KI0=0.008。

(11)

六旋翼飞行器的姿态解算准确性，分为静态误差和动态误差两部分。静态误差保证了六旋翼飞行器起飞前的姿态以及起飞后姿态保持不变的情况下的准确性；动态误差保证了六旋翼飞行器飞行过程中受外界扰动影响导致速度变化的情况下姿态解算的准确性。

3.2 静态测试

静态测试下，由于六旋翼飞行器速度为0，AECF和ECF中的KP，KI取值相同，即控制效果一样。取KP=KP0=0.2，KI=0.008。六旋翼飞行器在静止时刻经自适应互补滤波和陀螺仪的姿态角对比曲线如图4所示。

图4 静态情况下输出的姿态角

由图4(a)和4(b)可知，实际的初始位置不能保证绝对水平。经过互补滤波后，在静止时刻，飞行器的俯仰角横滚角都收敛。但是，经过一段时间后，仅靠陀螺仪输出的姿态角由于陀螺仪的漂移特性而呈现发散趋势。所以无法满足姿态解算的可靠性要求。定义姿态解算的误差为图2中误差向量e的模，静态误差实验数据如图5所示。

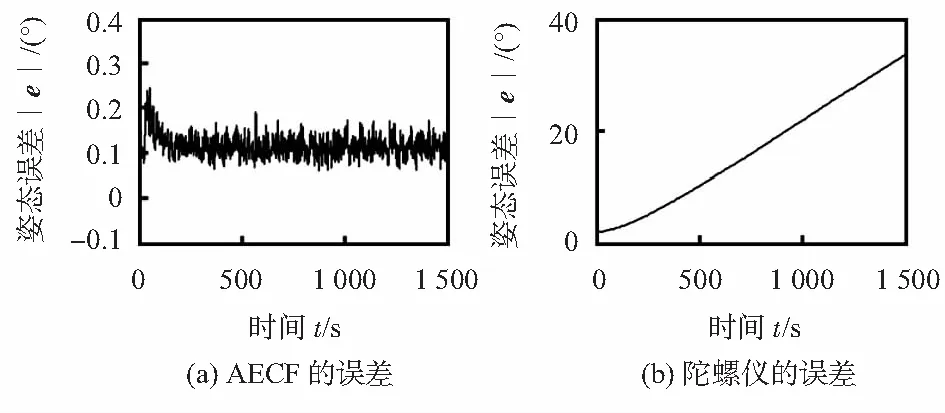
图5 静态测试下输出误差

由图5(a)可知，AECF算法姿态解算的误差基本保持在小于0.2°的范围内。由图5(b)可知，陀螺仪姿态误差逐渐增加，不满足系统的稳定性。

考虑电机振动带来的噪声影响，选择六旋翼飞行器的飞行模式为悬停自稳定模式，在姿态闭环控制的情况下，六旋翼飞行器在一定范围内保持水平，受电池续航能力的限制，测试时间为400 s。静态测试结果如图6所示。

由图6(a)可知，在悬停模式下六旋翼飞行器的横滚角φ对期望值的跟踪性能良好。由图6(b)可知，在初始状态下，受机体姿态期望值的影响，机体姿态处于摆动状态。当机体达到稳定状态后横滚角误差由初始转态的4°收敛到低于0.5°范围内。结果表明：在振动噪声下AECF算法姿态解算的准确性。

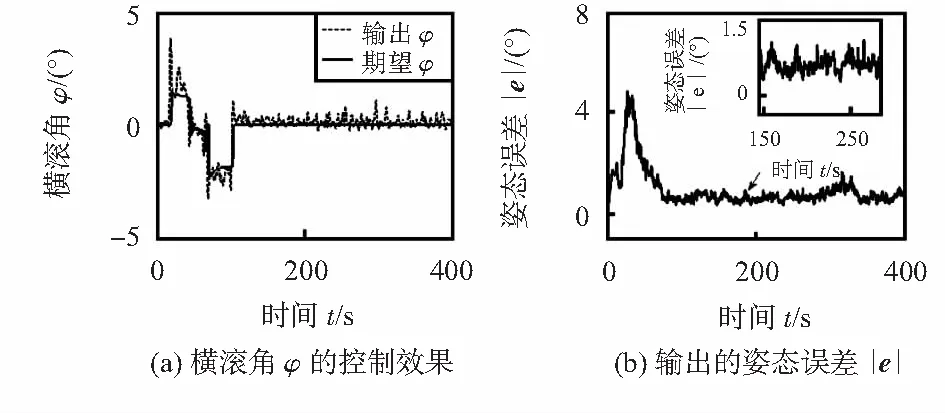
图6 悬停模式的静态测试

3.3 动态测试

六旋翼飞行器在飞行过程中，尤其是杂技等动作存在姿态角剧烈变化的情况。本文搭建了一个简易的实验测试装置用于模拟飞行器的姿态变化环境，如图7所示。

图7 机体动态实验测试装置

该装置的工作原理是由计算机给驱动器发送脉宽调制(PWM)信号，通过驱动器驱动步进电机，输出恒定的旋转速度，且飞控与电机输出轴之间刚性连接。该装置可用于动态测试下AECF和ECF算法的性能对比实验。动态测试下取AECF和ECF的初始Kp=0.2，KI=0.008。由于机体的横滚角和俯仰角具有对称性，仅选择横滚角速度ωx作为研究对象。测试输出的机体速度曲线如图8所示，不同算法输出的误差曲线如图9所示。

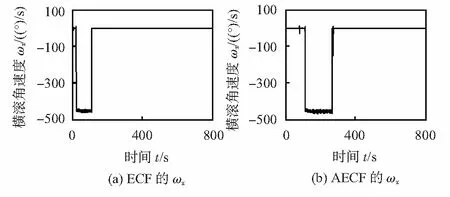
图8 步进电机输出横滚角速度ωr

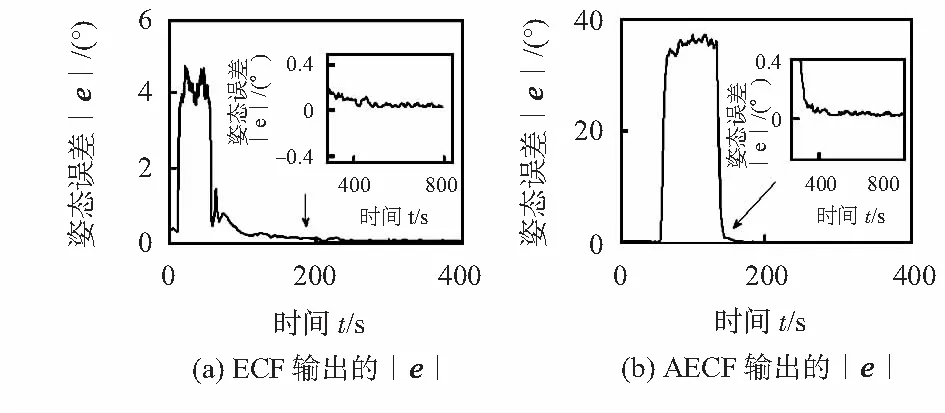
图9 姿态误差|e|

由图8，图9(a)可知：当机体横滚角速度为-450°/s时采用ECF算法输出动态误差最大4°～6°。采用AECF算法，其输出横滚角的动态误差为30°～40°。由此可得，AECF算法比ECF算法动态误差小，但是信号的毛刺比ECF严重。在300～800s之间，机体角速度为0°，AECF和ECF算法中的横滚角都达到稳态且稳态误差低于0.2°。

4 结束语

本文搭建以STM32F427为核心控制器的六旋翼飞行器系统以及静、动态测试平台。静、动态测试结果如下：1)在静态测试中AECF和ECF的补偿系数KP，KI参数相同。实验表明：AECF能保证姿态解算收敛，并且误差向量低于0.2°，而陀螺仪传感器解算效果发散；六旋翼飞行器存在机体噪声的情况下，AECF算法下的姿态解算结果依然能保持稳定状态。2)在动态测试中，AECF比ECF动态精度更高。

[1] 戴定成，蔡宗平，牛 创.基于容积卡尔曼滤波的自适应IMM算法[J].现代雷达，2015，37(3)：27-30.

[2]YunX,AparicioC,BachmannER.Implementationandexperimentalresultsofaquaternion-basedKalmanfilterforhumanbodymotiontracking[J].IEEETransactionsonRobotics,2006,22(6):1216-1227.

[3]AbasN,LegowoA,IbrahimZ.Modelingandsystemidentification

usingextendedKalmanfilterforaquadrotorsystem[J].AppliedMechanics&Materials,2013,313-314:976-981.

[4] 夏 楠,邱天爽,李景春,等.一种卡尔曼滤波与粒子滤波相结合的非线性滤波算法[J].电子学报,2013, 41(1)：148-152.

[5] 曲仕茹,马志强.改进的粒子滤波在四旋翼姿态估计中的应用[J].飞行力学,2013,31(5):458-461.

[6] 郭晓鸿，杨 忠，陈 喆,等.EKF和互补滤波器在飞行姿态确定中的应用[J].传感器与微系统,2011,30(11):149-152.

[7] 付勇杰,丁艳红,梁义维,等.动态倾角传感器及其传递特性的研究[J].仪表技术与传感器,2012(9):6-8.

[8]MahonyR,HamelT,PflimlinJ.Nonlinearcomplementaryfiltersonthespecialorthogonalgroup[J].IEEETransactionsonAutomaticControl,2008,53(5):1203-1218.

[9]EustonM,CooteP,MahonyR,etal.Acomplementaryfilterforattitudeestimationofafixed-wingUAV[C]∥IEEEInternationalConferenceonIntelligentRobotsandSystems,Nice,France:2008:340-345.

[10] 王 立，章 政，孙 平.一种自适应互补滤波姿态估计算法[J].控制工程，2015(5):881-886.

[11] 张承岫,李铁鹰,王耀力,等.基于MPU6050和互补滤波的四旋翼飞控系统设计[J].传感技术学报,2016,29(7):1011-1015.

[12] 傅忠云,刘文波,孙金秋,等.自适应混合滤波算法在微型飞行器姿态估计中的应用[J].传感技术学报,2014(5):698-703.

[13]WuZM,SunZG,ZhangWZ,etal.Anovelapproachforattitudeestimationbasedonmemsinertialsensorsusingnonlinearcomplementaryfilters[J].IEEESensorsJournal,2016,16(10):1.

[14] 孙金秋,游有鹏,傅忠云,等.基于自适应显式互补滤波的姿态解算方法[J].测控技术,2015, 4(4):24-27.

刘 洲(1993- )，男，硕士研究生，主要研究方向为惯性传感器的姿态解算以及六旋翼飞行器的控制算法，E—mail：liuzhou2015@csu.edu.cn。

Application of adaptive explicit complementary filtering in six-rotor aircraft*

LIU Zhou, SHAN Xiu-yang, TAN Fang

(School of Mechanical and Electrical Engineering,Central South University,Changsha 410083,China)

To solve the drift problem of inertial sensor of six-rotor aircraft during the measurement process,a attitude estimation algorithm based on adaptive explicit complementary filtering(AECF)is proposed.The principle and stability of the proposed algorithm are analyzed.A six-rotor aircraft experimental test device is set up to carry out static and dynamic experiment of the aircraft.Adaptive explicit complementary filtering algorithm,explicit complementary filtering algorithm and gyroscope sensor measurement are compared in the experiment.The experimental results show that the adaptive explicit complementary filtering algorithm can make the solution attitude error of sensor gradually converge and its dynamic error is the smallest.

adaptive explicit complementary filtering; six-rotor aircraft; attitude estimation; inertia sensor; gyroscope

10.13873/J.1000—9787(2017)05—0157—03

2017—07—17

国家“973”计划基金资助项目(2011CB013104)；中南大学中央高校基本科研业务费专项资金资助项目

V 249

A

1000—9787(2017)05—0157—04