填料塔支承圈及栅板校核有限元分析

黄文霞

（中国石油大学（华东）)

填料塔支承圈及栅板校核有限元分析

黄文霞*

（中国石油大学（华东）)

应用有限元软件ANSYS建立某填料塔器支承圈及栅板的力学模型，计算分析了支承圈和栅板的强度、刚度并进行了栅板屈曲分析，得到了支承圈及栅板在工作状态下的应力和位移分布规律及屈曲临界载荷。分析表明，栅板及支承圈不会发生强度和刚度失效。但从长期使用考虑，应对栅板进行适当加固。支承圈采用矩形截面结构并不合理。

栅板 支承圈 填料塔 有限元 力学模型 载荷 强度

某炼油厂车间扩量改造时新增一填料塔，塔内径为2000 mm，塔内填料支承圈材质为普通碳钢，结构简单，塔内部填料及栅板质量约为 8000 kg，填料由栅板支承。为了保证设备长期稳定运行，避免塔内填料脱落，本文对支承圈及填料支承栅板应用ANSYS进行了有限元分析，可为工程应用提供一定的指导。

1 支承圈有限元分析

1.1 有限元模型[1]

由于支承圈和塔器为轴对称结构，所以建立轴对称模型进行分析。支承圈与筒体满焊连接，连接部位设置半径为2 mm的倒角。支承圈与塔器筒体的几何尺寸及材料参数见表1，其模型及网格划分如图1所示。

1.2 边界条件与载荷

塔器筒体上下端面限制其轴向位移，力学模型可简化成悬臂梁。在支承圈上表面施加栅板对其的作用压力集度：

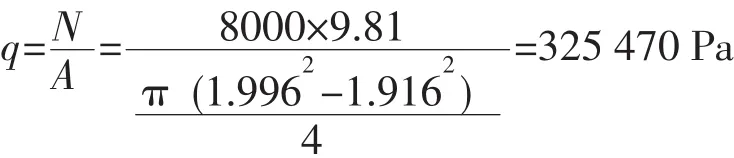
表1 几何尺寸及材料参数

图1 支承圈与塔器筒体网格划分

1.3 强度分析

支承圈承受栅板及填料的质量较大，为了避免填料脱落，必须保证其有足够的强度。

计算得到的支承圈与塔壁处的径向应力、轴向应力、轴向切应力以及mises应力强度云图分别如图2～图5所示。支承圈在栅板及填料压力作用下，在支承圈的焊接根部上下表面的径向应力存在最大值，分别为33.4 MPa和-33.2 MPa；在支承圈与塔壁的焊接部位上下表面的轴向应力存在最大值，分别为15.9 MPa和-15.8 MPa。同样，在支承圈与塔壁的焊接部位上下表面的切向应力存在最大值，为15.2 MPa。在支承圈与塔壁的焊接部位并靠近支承圈附近上下表面区域的应力强度存在最大值，其值为29.8 MPa。

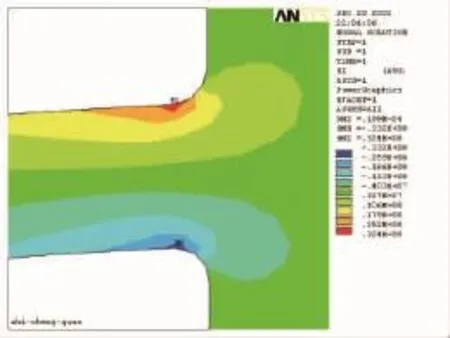
图2 支承圈与塔器径向应力 （SX）

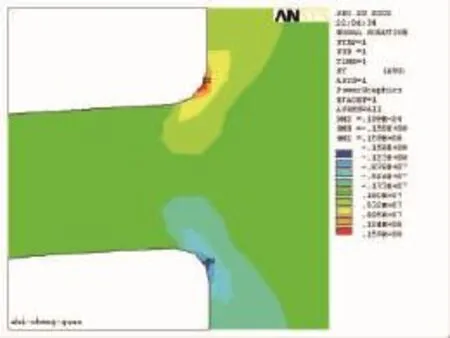
图3 支承圈与塔器轴向应力 （SY）

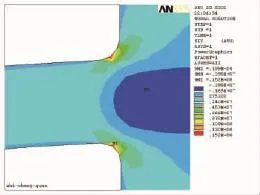
图4 支承圈与塔器切应力 （SXY）

图5 支承圈与塔器mises应力强度 （SEQV）

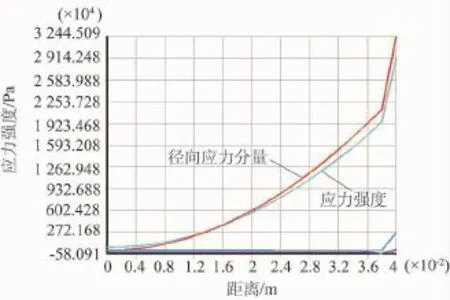
图6支承圈上表面应力强度及应力分量沿半径方向变化图

图6 为支承圈上表面应力强度及应力分量沿半径方向变化图，其中深色线 （红线）为径向应力分量，浅色线 （浅兰线）为应力强度。显然，在应力强度中占主导地位的是支承圈表面径向应力分量，但应力总体水平较低，最大值仅为33.4 MPa。这说明支承圈不会发生强度失效。

由于支承圈为矩形截面的环板，与筒体焊接为一体，焊缝处为危险截面，在最大应力作用下，容易出现强度破坏。尤其在腐蚀环境下，更容易出现应力腐蚀破坏。因此从结构上看，采用矩形截面的环板并不合理。但一味保证强度又会造成材料浪费，建议优选梯形截面。

1.4 刚度分析

在保证强度的前提下，需要校核支承圈刚度，避免支承圈变形过大导致栅板脱落。

支承圈在栅板及填料压力作用下，支承圈的径向变形、轴向变形以及绝对变形云图如图7～图9所示。支承圈内径自由端的轴向位移存在最大值为0.019 8 mm。

图7 支承圈的径向变形 （UX）

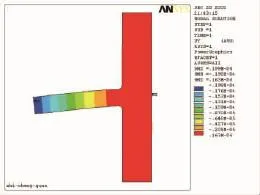
图8 支承圈的轴向变形 （UY）

图10 为支承圈上表面径向位移、轴向位移和绝对位移沿半径方向变化图。显然，在支承圈内径的自由端各位移分量及绝对位移存在最大值，轴向位移最大值为 0.019 8 mm，绝对位移最大值为0.019 9 mm。

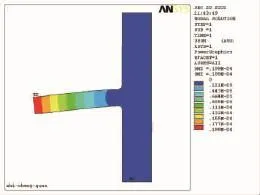
图9 支承圈的绝对变形 （USUM）

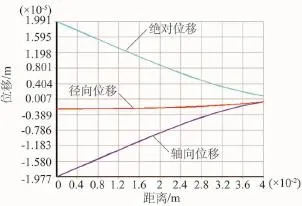
图10 支承圈上表面径向位移、轴向位移和绝对位移沿半径方向变化图

2 栅板有限元分析

2.1 有限元模型

栅板几何尺寸及材料参数见表2。栅板整体由五块组成。其中，中间块长度最大，由 20根40 mm×6 mm的栅板条，通过40 mm×6 mm的边梁焊接成一体。由于该块栅板搭在支承圈上，所以将栅板条简化为两端简支梁，建立有限元计算模型。

表2 栅板几何尺寸及材料参数

2.2 强度和刚度分析

根据简支梁受均布载荷的力学模型，对栅板的内力和变形计算如下。

栅板单位长度压力分布集度：

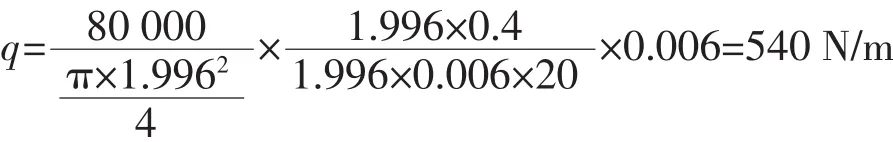
惯性矩：Iz＝3.2×10-8m4

栅板横截面面积：A＝2.4×10-4m2

抗弯截面系数：Wz＝1.6×10-6m3

最大弯矩：Mmax＝ql2/8＝540×1.9962/8＝269 N·m

栅板最大挠度：

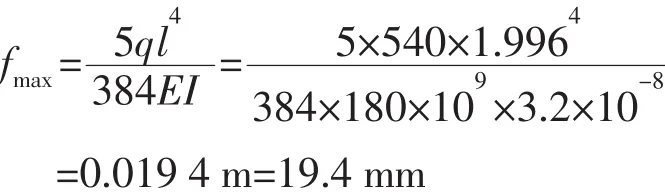
栅板的内应力和变形有限元计算如图11～图14所示。

图11 截面弯曲正应力

图12 截面mises相当应力

图13 截面轴线方向位移

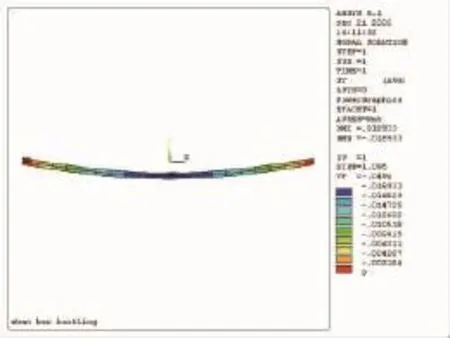
图14 截面挠度

通过以上对栅板条简支条件下的强度和刚度分析，理论计算结果与有限元计算基本吻合。

栅板最大挠度:

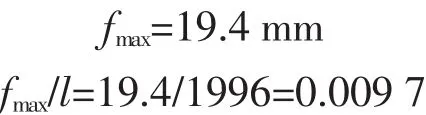
最大弯曲正应力:

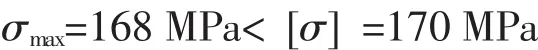
满足强度要求。

由计算结果可知，栅板中间部位的应力和挠度最大。

2.3 屈曲分析

栅板两端简支条件下屈曲安全系数及其临界载荷如表3所示。栅板发生一阶弹性屈曲时，两端简支栅板的安全系数为1.759 5。

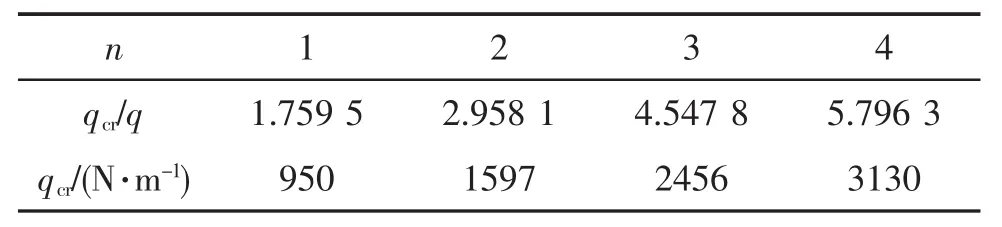
表3 屈曲安全系数及其临界载荷

图15 栅板的一阶屈曲变形图

图15 ～图18为栅板不同阶次屈曲变形图。从图中可以看出，栅板发生一阶弹性屈曲时临界载荷最小，位移最大。

图16 栅板的二阶屈曲变形图

图17 栅板的三阶屈曲变形图

图18 栅板的四阶屈曲变形图

3 结论

本文应用有限元软件ANSYS建立某填料塔器支承圈及栅板的力学模型，计算分析了支承圈和栅板的强度、刚度并进行了栅板屈曲分析，得到了支承圈及栅板在工作状态下的应力和位移分布规律及屈曲临界载荷。

通过以上对支承圈及栅板的有限元分析，可得如下结论：

（1）在支承圈与塔壁的焊接部位并靠近支承圈附近上下表面区域应力强度存在最大值，表面径向应力分量水平较高，在应力强度中占主导地位，但应力总体水平较低。

（2）支承圈与筒体焊接处为最大应力处。在支承圈内径的自由端各位移分量及绝对位移中存在最大值，位移最大值为0.019 8 mm。支承圈采用矩形截面结构并不合理。

（3）在栅板中间部位挠度和应力值最大，栅板发生一阶弹性屈曲时临界载荷最小，位移最大。

（4）通过以上对支承圈、栅板的强度和刚度分析可知，支承圈不会发生强度和刚度失效，栅板设计符合要求，可以正常使用。但考虑到栅板的使用环境存在腐蚀性物质，根据计算结果，从长期使用考虑，建议对栅板进行适当加固，防止栅板发生屈曲变形。

[1]刘涛，杨凤鹏.精通ANSYS[M].北京：清华大学出版社，2002.

Checking of the Supporting Ring and the Grid of a Packed Tower with Finite Element Method

Huang Wenxia

The mechanical model for the supporting ring and the grid of a packed tower is established by using finite element software ANSYS.By calculating the strength and stiffness of the supporting ring and the grid and analyzing the buckling of the grid,the stress and displacement distribution of the supporting ring and the grid under working conditions are obtained,and the critical buckling load of the grid is also obtained.Analysis shows that the strength and stiffness failure of the grid and the supporting ring will not occur.However,considering the long-term use,it is necessary to strengthen the grid properly.And it is not reasonable to use rectangular section structure for the supporting ring.

Grid;Supporting ring；Packed tower;Finite element;Mechanical model;Load;Strength

TQ 050.3

10.16759/j.cnki.issn.1007-7251.2017.04.001

2016-08-26）

*黄文霞，女，1974年生，硕士，高级工程师。东营市，257061。