两招定切线解题特方便
陈焕芬 王锋
两招定切线解题特方便
陈焕芬 王锋
直线与圆有一种特殊的位置关系,那就是——相切,如何判定一条直线是圆的切线,有两种常见判定方法:①到圆心的距离等于圆的半径的直线是圆的切线;②经过半径的外端点并且垂直于这条半径的直线是圆的切线.
一、无公共点,作“垂线”,证“等于半径”
例1如图1,在△ABC中,AB=AC,O是BC的中点,以点O为圆心的⊙O与AC相切于点D.求证:⊙O与AB相切.
【思路突破】根据切线的性质可知⊙O的半径OD⊥AC,根据“圆心到直线的距离等于半径的直线是圆的切线”,只需证明点O到AB的距离等于OD即可.
证明:如图1,连接AO,OD,过点O作OE⊥AB于点E.∵AC是⊙O的切线,切于D,
∴OD⊥AC.
∵AB=AC,O是BC的中点,
∴AO平分∠BAC.
又∵OD⊥AC,OE⊥AB,
∴OD=OE,∴⊙O与AB相切.
【点评】由于题目未明确指出AB与⊙O是否有公共点,只需过圆心作直线AB的垂线段,证明垂线段的长等于半径即可.
例2如图2,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A、与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
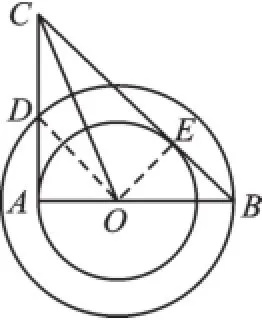
图2
(1)试判断BC所在直线与小圆的位置关系;(2)试判断线段AC、AD、BC之间的数量关系.
【思路突破】(1)根据题意无法判定线段BC所在直线与小圆是否有公共点,因而可以选择判定方法①.为此可过点O作BC所在直线的垂线段OE,只需证明OE=OA(⊙O的半径)即可.
(2)由(1)可知CA=CE,只需说明BE=AD,便可以猜想到AC+AD=BC.
解:(1)BC所在直线与小圆相切.
理由如下:过圆心O作OE⊥BC,垂足为E,
∵AC是小圆的切线,AB经过圆心O,
∴OA⊥AC,
又∵CO平分∠ACB,OE⊥BC,∴OE=OA,
∴BC所在直线与小圆相切.
(2)AC+AD=BC.
理由如下:连接OD.∵AC切小圆O于点A,BC切小圆O于点E,∴CE=CA.
∵在Rt△OAD与Rt△OEB中,OA=OE,OD= OB,∠OAD=∠OEB,∴Rt△OAD≌Rt△OEB,
∴EB=AD,∴BC=AC+AD.
【点评】证明线段之间的和差关系,通常是在长线段上截取一段等于短线段,再证剩余的线段等于另一条线段即可.
二、连“半径”证“垂直”
例3如图3,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB于点E,ME=1,AM=2,AE=3,求证:BC是⊙O的切线.
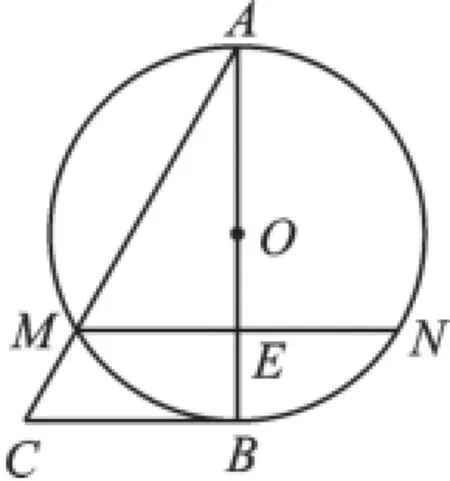
图3
【思路突破】BC经过半径OB的外端,因此只需证明OB⊥BC即可.
证明:∵ME=1,AM=2,AE=3,
∴△AME是直角三角形.
又∵MN∥BC,∴∠ABC=∠AEM=90°.
∴BC是⊙O的切线.
【点评】当已知三角形的三边的长度时,可以根据“两短边的平方和等于最长边的平方”,来说明此三角形为直角三角形,进而确定线段互相垂直的关系.
例4如图4,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
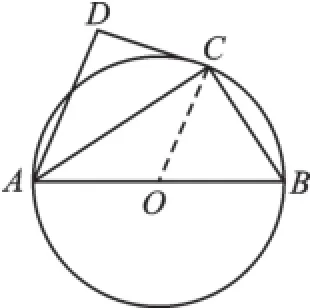
图4
【思路突破】(1)直径所对的圆周角为直角,利用勾股定理求得AC=4;(2)连接OC,证OC⊥CD即可.
解:(1)略.
(2)证明:连接OC,
∵OA=OC,∴∠OAC=∠OCA,
又∵AC是∠DAB的角平分线,
∴∠DAC=∠BAC,∴∠DAC=∠OCA,
∴OC∥AD,又∵AD⊥DC,∴OC⊥CD,
∴DC是⊙O的切线.
【点评】要证直线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.
例5如图5,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.
(1)用直尺画出该圆弧所在圆的圆心M的位置;
(2)若A点的坐标为(0,4),D点的坐标为(7,0),求证:直线CD是⊙M的切线.
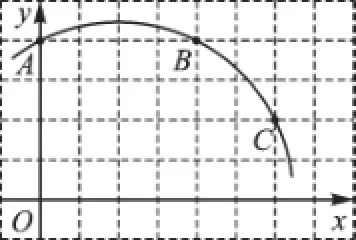
图5
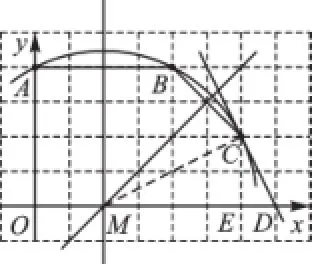
图6
【思路突破】(1)连接AB、BC,根据网格画出它们的垂直平分线,其交点就是圆心M的位置.(2)欲证直线CD是⊙M的切线,只需证∠MCD=90°即可.
解:(1)如图6.
(2)证明:由A(0,4),可得小正方形的边长为1,从而得C(6,2).如图6,设过C点与x轴垂直的直线与x轴的交点为E,连接MC,作直线CD.
∴CE=2,ME=4,ED=1,MD=5,
在Rt△CEM中,∠CEM=90°,
∴MC2=ME2+CE2=42+22=20.
在Rt△CED中,∠CED=90°,
∴CD2=ED2+CE2=12+22=5,
∴MD2=MC2+CD2,
∴∠MCD=90°,又因为MC为半径,
∴直线CD是⊙M的切线.
【点评】以网格为背景的问题,要充分发挥网格中的平行与垂直关系,挖掘出隐含的直角三角形、矩形、正方形及全等三角形等基本的图形,以便利用其基本图形的性质,帮助我们解决相关的问题.
(作者单位:江苏省丰县实验中学)

