“圆”中渗透的数学思想

赵传东

“圆”中渗透的数学思想

赵传东

数学思想是人们对数学活动经验的概括和总结，是数学基础知识及基本技能的本质体现，是数学知识的提炼、升华和结晶，是解决数学问题的灵魂.本文就带你到“圆”形世界去挖掘其中所蕴含的分类思想和转化思想，领略其美丽的风采.

一、圆中的分类思想

由于圆既是轴对称图形，又是中心对称图形，在没有明确图形位置的情况下，符合题意的图形可能有多种.因此在本章中应注意圆的问题的多样性，不要忘记分情况讨论.

1.点和圆位置关系中的分类讨论.

例1如图1，直线AB与⊙O相切于B点，C是⊙O与OA的交点，点D是⊙O上的动点（D与B、C不重合），若∠A=40°，则∠BDC的度数是（）.

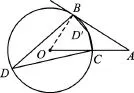
图1

A.25°或155°B.50°或155°

C.25°或130°D.50°或130°

【分析】点D可以在劣弧上，也可以在优弧上.

解：当点D在优弧BC上时，如图1，连接OB，∵直线AB与⊙O相切于B点，∴∠OBA= 90°，∠AOB=50°，∠BDC=∠AOB=25°；

∴∠BDC的度数为25°或155°.

【点评】本题考查了切线的性质、圆周角定理以及圆的内接四边形的性质.由于点D既可在优弧BC上，也可在劣弧BC上，所以要分两种情况讨论.

2.直线和圆位置关系中的分类讨论.

例2如图2，平面直角坐标系xOy中，半径为2的⊙P的圆心P的坐标为（-3，0），将⊙P沿x轴正方向平移，使⊙P与y轴相切，则平移的距离为（）.

A.1B.1或5C.3D.5

图2

【分析】⊙P可以在y轴的左边也可以在y轴的右边.

解：当⊙P位于y轴的左侧且与y轴相切时，平移的距离为1；当⊙P位于y轴的右侧且与y轴相切时，平移的距离为5.故选B.

按照国务院对地理国情监测工作总体部署和测绘地理信息事业转型发展需要，从2016年起地理国情信息获取进入常态化监测阶段。本文通过对在地理国情监测生产中频发性、关键性问题的分析，总结归纳了基础性地理国情监测成果质量控制的方法。

【点评】本题主要考查了切线的性质的应用等知识，由于圆P在运动过程中，既可能和y轴左边相切，也可能和y轴右边相切，所以要分情况讨论.

3.圆与圆位置关系中的分类讨论.

例3以O为圆心的两个同心圆中，大圆与小圆的半径分别为3cm和1cm，若圆P与这两个圆都相切，则圆P的半径为.

【分析】圆P既可以和小圆内切同时也可以和小圆外切.

解：①若圆P与小圆外切，如图3（1），此时圆P的半径=1 2（3-1）=1（cm）；P的半径

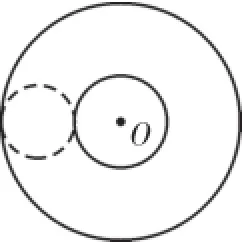
图3 （1）

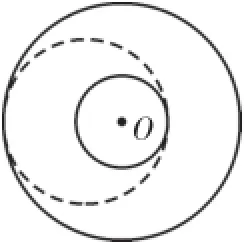
图3 （2）

【点评】本题主要考查圆与圆的位置关系，虽然圆P只能和大圆内切，但和小圆既可内切，也可外切.所以两圆相切，应分情况讨论.

二、圆锥中的转化思想

例4如图4所示，圆锥的母线OA=8，底面的半径r=2，若一只小虫从A点出发，绕圆锥的侧面爬行一周后又回到A点，则小虫爬行的最短路线的长是.

【分析】将圆锥沿一条母线剪开，其侧面展开图是一个扇形，小虫从A点出发，绕圆锥的侧面爬行一周后又回到A点，爬行的︵最短路线的长实际上是扇形中弦AB的长度.AB的长度就是圆锥的底面周长.

图4

【点评】对于立体图形研究两点间的最短距离，往往是先把立体图形展开成平面图形，再根据“在平面内两点之间线段最短”的性质解决.解决的关键是明确展开前后有关图形的对应关系.

例5如图5，在Rt△ABC中，AC=BC= 2 2，若把Rt△ABC绕斜边AB所在的直线旋转一周，则所得几何体的表面积为（）.

A.4πB.4 2πC.8πD.8 2π

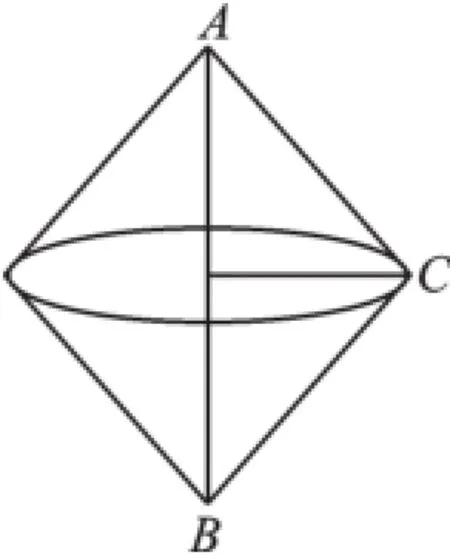
图5

【分析】Rt△ABC绕斜边AB所在的直线旋转一周形成两个圆锥，而且两个圆锥的形状完全相同.求所得几何体的表面积的关键是求出锥体的底面半径.

【点评】绕直角三角形的斜边旋转，首先要搞清直角三角形的直角边是圆锥的母线，斜边上的高是圆锥的底面圆半径.所以明确圆锥侧面展开图的扇形的弧长、半径与圆锥的底面圆周长、母线的对应关系是解决本题的关键.

（作者单位：江苏省丰县初级中学）