勾股定理在圆中的应用
史新景
勾股定理在圆中的应用
史新景
勾股定理是初中数学中的一个重要定理,在有关几何的证明与计算题中到处可以看到它的身影,在圆的世界中更是如此.本文通过以下几个实例说明勾股定理在圆中有着广泛的应用.
一、勾股定理与垂径定理
例1如图1所示,某窗户由矩形和弓形组成,已知弓形的跨度AB=3m,弓形的高︵EF= 1m,现计划安装玻璃,请帮工程师求出AB所在圆的半径.
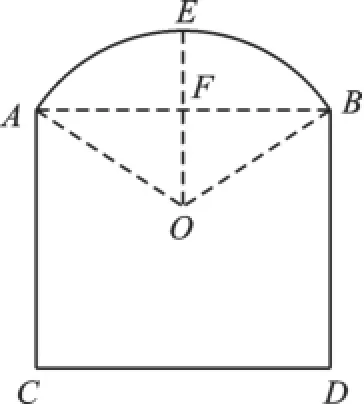
图1
【分析】弦心距用半径来表示是解决问题的关键,设半径为r,则弦心距为r-1,根据勾股定理可得方程,从而问题得解.
设AO=r,则OF=r-1,
在Rt△AOF中,AO2=OF2+AF2,
【点评】此类题目中垂径定理与勾股定理如影相随,通常采用把半弦、弦心距、半径三者放到同一个直角三角形中,利用勾股定理解答.
二、勾股定理与切线长定理
例2如图2,Rt△ABC中,∠C=90°,BC= 5,Rt△ABC的内切圆O与三边分别相切于点D、E、F,半径r=2,求△ABC的周长.
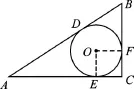
图2
【分析】见切点,连半径,得垂直,连接OE,OF,得到四边形OECF为正方形,CE=CF=r=2,因为BC=5,所以BF=BD=3,要求三角形的周长只需要求出AD,AE的长度,设为x,在直角三角形中运用勾股定理即可求解.
解:连接OE、OF,设AD=x,则AE=AD=x,
∵点D、E、F是切点,∴OE⊥AC,OF⊥BC,
又∵∠C=90°,OE=OF,
∴四边形OECF为正方形,
∵⊙O的半径为2,BC=5,
∴CE=CF=2,BD=BF=3,
在Rt△ABC中,∵AC2+BC2=AB2,
即(x+2)2+52=(x+3)2,∴x=10,
∴AC=12,AB=13,
∴△ABC的周长为12+5+13=30.
【点评】本题主要考查切线长定理、正方形的判断和勾股定理的应用,连接OE、OF,构造正方形OECF是解题的关键.
三、勾股定理与内切圆
例3某新建小区要在一块等边三角形的公共区域内修建一个圆形花坛.
(1)若要使花坛面积最大,请你在这块公共区域(如图3(1))内确定圆形花坛的圆心P;
(2)若这个等边三角形的边长为18m,请计算出花坛的面积.
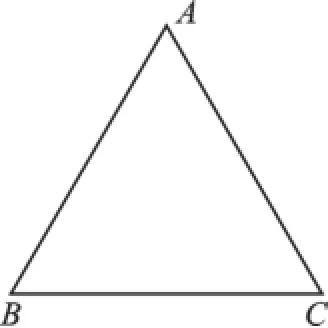
图3 (1)
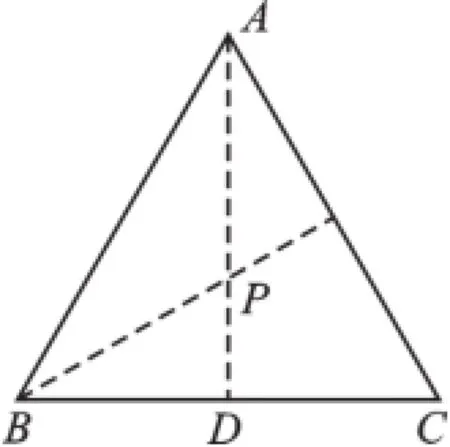
图3 (2)
【分析】(1)在△ABC内作一个内切圆,则此圆面积最大,点P为角平分线的交点.(2)注意到Rt△BPD一个锐角为30°,BP=2PD,再利用勾股定理问题就迎刃而解了.
解:(1)见分析如图3(2);
(2)在Rt△BPD中,BD=9m,∠PBD=30°,设PD=x,则BP=2x,由勾股定理得:x2+92=(2x)2,解得
【点评】要使花坛的面积最大,作出三角形的内切圆即可.
四、勾股定理与正多边形
例4一个亭子的地基是半径(外接圆半径)为8m的正六边形,求地基的周长与面积.
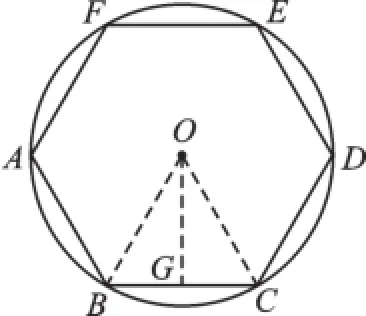
图4
【分析】正六边形的中心角是60°,易知△OBC是正三角形,边长等于半径,周长为半径的六倍,正六边形的面积为△OBC面积的六倍.
解:连接OB、OC,∵∠BOC=60°,
∴△OBC是正三角形,∴BC=OB=8m,
∴正六边形ABCDEF的周长=6×8=48(m).
过O作OG⊥BC于G,
在Rt△BOG中,由勾股定理得
【点评】本题考查的是正六边形、等边三角形的性质及勾股定理,难度不大,注意掌握数形结合思想的应用,掌握辅助线的作法是解此题的关键.
五、勾股定理与切线
例5(2016·哈尔滨)如图5,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接OC、BE.若AE=6,OA= 5,则线段DC的长为.
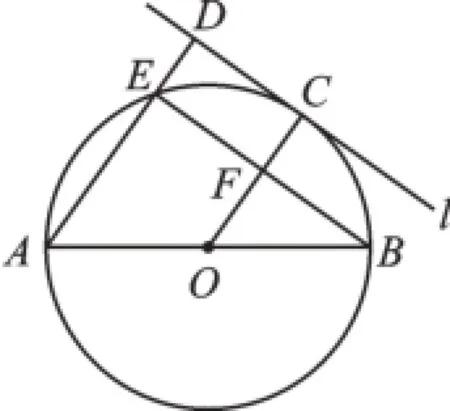
图5
【分析】OC交BE于F,如图5,由圆周角定理得到∠AEB=90°,加上AD⊥l,则可判断BE∥CD,再利用切线的性质得OC⊥CD,则OC⊥BE,可判断四边形CDEF为矩形,所以CD=EF,接着利用勾股定理计算出BE,然后利用垂径定理得到EF的长,从而得到CD的长.
解:OC交BE于F,如图5,
∵AB为⊙O的直径,
∴∠AEB=90°,
∵AD⊥l,∴BE∥CD,
∵CD为切线,
∴OC⊥CD,∴OC⊥BE,
∴四边形CDEF为矩形,
∴CD=EF,
∵OF⊥BE,∴BF=EF=4,∴CD=4.
江苏省丰县初级中学)

