IPSO-MPC算法在智能车纵向速度控制中的应用
周晶晶,徐友春,张自立,李明喜,苏致远
(1.蚌埠汽车士官学校 运输勤务系,安徽 蚌埠 233011; 2.军事交通学院 军用车辆系,天津 300161;3.军事交通学院 研究生管理大队,天津 300161)
● 车辆工程 Vehicle Engineering
IPSO-MPC算法在智能车纵向速度控制中的应用
周晶晶1,徐友春2,张自立1,李明喜2,苏致远3
(1.蚌埠汽车士官学校 运输勤务系,安徽 蚌埠 233011; 2.军事交通学院 军用车辆系,天津 300161;3.军事交通学院 研究生管理大队,天津 300161)
基于模型预测控制(MPC)理论的智能车纵向速度控制问题可以转换为二次规划问题(QP)。针对该QP问题,利用一种改进的粒子群算法(IPSO)减少MPC计算成本。通过引入收缩因子保证粒子群算法收敛,引入惯性因子避免粒子在全局最优解附近振荡,引入“备胎机制”来处理QP约束。数值试验验证了改进的IPSO算法可减少迭代次数、降低计算成本。将IPSO算法与MPC算法结合形成IPSO-MPC算法,智能车纵向速度控制仿真结果证明IPSO-MPC算法有效。
纵向速度控制;智能车;粒子群算法;模型预测控制
模型预测控制(model predictive control,MPC)算法是19世纪80年代发展起来的一类控制算法[1]。粒子群算法(particle swarm optimization,PSO)是一种基于鸟类群体行为仿真的随机优化算法。PSO算法规则简单、收敛速度快、可调参数少,并具有群体智能,已广泛应用于函数优化、神经网络训练和模糊控制系统等领域[2]。目前MPC在智能车控制应用中面临的主要问题是在优化目标较多时计算成本较高,影响控制系统实时性的要求。为降低计算成本,提高控制的响应速度,文献[3]提出减少目标函数和确定预测时域的方法降低计算成本;文献[4]以可编程逻辑门阵列(FPGA)为平台实现了PSO-MPC控制器;文献[5]在粒子更新过程中加入收缩因子以保证PSO收敛;文献[6]增加扰动项来更新粒子速度,并用简化的k-最近邻算法动态调整粒子生存期;文献[7]将PSO算法和混合蛙跳算法结合起来,将粒子群进行分组搜索,各组利用不同公式进行迭代更新以保证粒子的差异性;文献[8]将基于MPC理论的、多变量多约束的智能车纵向速度控制问题转化为二次规划(quadratic programming,QP)问题。
本文在此基础上,通过改进的粒子群算法(improved PSO,IPSO)来求解QP问题:通过引入收缩因子保证粒子群算法收敛、引入惯性因子避免粒子在全局最优解附近振荡、引入“备胎机制”来处理QP约束,而后将IPSO与MPC结合形成IPSO-MPC算法来求解带约束的MPC问题。
1 基本PSO算法
文献[8]将基于车间运动学和MPC理论的智能车纵向速度控制问题转换为带有等式、不等式约束的QP问题。为求解此QP问题,首先对基本粒子群算法(basic PSO,BPSO)进行改进。

(1)
式中:正常数c1、c2为学习因子,分别调整粒子飞向局部、全局最优位置的步长,一般取c1=c2=2;r1、r2为相互独立且服从[0,1]上均匀分布的两个随机数;vin(k)为粒子速度,满足约束vin(k)∈[-vmax,vmax],vmax为粒子最大速度;正常数ω为惯性因子,其大小调整粒子的局部、全局搜索能力;n为粒子i的第n维变量,n=1,2,…,N。
设目标函数为f(x),第i个粒子PiN计算式为
PiN(k+1)=
(2)
BPSO算法的流程如图1所示。
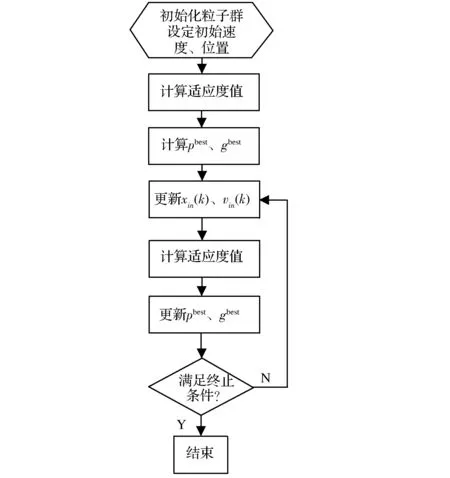
图1 BPSO算法流程
2 改进的PSO算法(IPSO)
在式(1)的基础上,对BPSO算法中粒子进化方式进行如下改进:
(3)
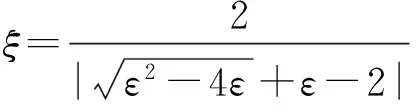
式(3)改进的粒子群算法速度更新方法中,引入收缩因子ξ可以保证BPSO收敛[11];加入动态调整惯性因子ω,避免粒子在全局最优解附近振荡;c1对应项反映了粒子的局部搜索能力;c2对应项反映了粒子的全局搜索能力;c3对应项反映了粒子利用过去行为预测未来搜索的能力。
为研究惯性因子ω对改进PSO算法的影响,使ω动态调整,设第k次进化取值为ωk,T为最大进化次数(k=1,2,…,T),分别为最大、最小惯性因子,为正常数。研究以下5种方法动态调节ωk:
ωk=ωmax-(ωmax-ωmin)k/T
(4-1)
ωk=ωmax-(ωmax-ωmin)(k/T)1.5
(4-2)
ωk=ωmax-(ωmax-ωmin)(k/T)2
(4-3)
ωk=ωmax-(ωmax-ωmin)[2k/T-(k/T)2]
(4-4)
ωk=ωmax-(ωmax-ωmin)T/(1+ck)
(4-5)
3 IPSO算法数值试验
利用Matlab实现上述IPSO算法,并与典型粒子群算法(以下简称BPSO算法)对比。使用式(5)经典测试函数,函数的图形如图2所示。
(5)

图2 经典测试函数
可以看到该测试函数在设定的搜索空间范围内有很多极大值点,而在原点处取得全局极大值(约为1.005 4)。用Matlab实现IPSO算法,并与BPSO算法进行对比,仿真参数为:T=300,M=20,vmax=1,ωmax=0.9,ωmin=0.4,c1=2.1,c2=2,c=10,ε=4.1,ξ=0.729 8。比较5种调节ωk方法,为分析IPSO算法性能,参数设置不变,各实验运行50次取均值,认为接近最优解范围为gbest∈[1.005 1-0.01,1.005 1+0.01],gbest在其他区间认为陷入局部最优解,其性能对比见表1。

表1 BPSO及IPSO性能对比
从表1可以看出,改进的算法均能明显减少进化代数,快速求出最优解,提高了BPSO算法效率。其中IPSO4算法收敛速度较快,陷入局部最优解次数少。将IPSO4算法作为最终改进的算法(IPSO),测试经典函数Rastrigin(R函数)和Schaffer(S函数),其函数表达式为
(6)
式中x,y∈[-5,5]。
仿真参数为:T=100,M=20,vmax=1,ωmax=0.9,ωmin=0.1,c1=2.1,c2=c3=2,c=10,ε=4.1,ξ=0.729 8。比较5种动态调节方法,IPSO和PSO算法各仿真10次取平均值,对比图形如图3所示,结果见表2。
从图3和表2的对比发现,IPSO算法与PSO都能找到全局最小值,但改进后IPSO算法收敛更快,寻优结果精度至少提高一个数量级,并能有效避免早熟现象。


图3 R函数、S函数IPSO、PSO适应度对比

函数全局最优位置平均最优值BPSOIPSOBPSOIPSOR9.673.460.3711.34S0.07070.001050.03190.00327
4 IPSO-MPC算法
将上述IPSO算法与MPC结合,求解文献[8]带有等式、不等式约束的QP问题。IPSO-MPC算法流程如图4所示。
为了处理QP约束,引入“备胎机制”,即每次更新完粒子的位置后,将新位置向量代入约束不等式,如果不满足约束,不直接将此粒子抛弃,而是将它的位置直接设置为当前的全局最优值(作为一个“备胎”)。在IPSO算法的基础上,为保证优秀粒子的影响力,将不满足约束的粒子的位置设置为全局最优值gbest。u(0),u(1),…,u(Nc-1)为MPC求解产生最优控制序列,只将u(0)作用于控制系统,为在初始化时提高IPSO-MPC算法效率,将u(1),…,u(Nc-1)作为粒子的gbest初值。

图4 IPSO-MPC算法流程
5 纵向速度控制Matlab仿真
为验证IPSO-MPC算法在智能车纵向速度控制中的应用效果,使用该算法解决文献[8]的智能车纵向速度控制问题。运用Matlab仿真,仿真参数值为:Np= 10,Nc= 2,d0=Δx=5 m,Ts= 0.1,χ= 1.2 s,T= 100,τ=0.5 s,Nmin= 1 500,ε=4.1,vh0= 5 m/s,c2=c3=2,M = 20,vmax=1,ωmax=0.9,ωmin=0.9,c1=2.1,c=10,ξ=0.729 8。输出变量权重系数和控制变量权重系数分别为0.6和0.8;约束条件为vhmin=0 m/s,vhmax= 25 m/s,ahmin= -0.5 m/s2,ahmax= 0.5m/s2。MPC目标速度设置为:0~1 s为5 m/s,1~50 s逐渐加速到18 m/s,50~100 s保持匀速18 m/s,100~150 s逐渐减速到静止。为保证纵向控制的平稳性和舒适性,取平稳趋近于目标速度的指数衰减函数作为参考速度。状态变量和输出变量仿真结果如图5所示。
仿真结果表明,智能车实际速度能快速跟踪目标速度,加速度满足其约束要求|ah|≤0.5 m/s2,保证了控制平稳性的要求。当预测时域Np≤ 50时,算法计算成本小于智能车实时控制周期100 ms,故可以满足控制实时性要求。

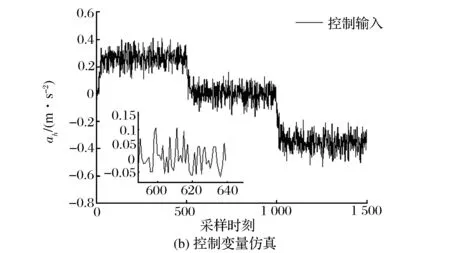
图5 速度与控制变量仿真结果
6 结 语
本文针对基于MPC的智能车纵向速度控制问题的二次规划问题,提出IPSO-MPC来求解该问题。引入收缩因子和变惯性权重因子对有PSO算法进行改进,引入“备胎机制”来处理MPC约束。
仿真实验证明:在满足约束的前提下,改进的算法减少了迭代次数和MPC计算成本。Matlab仿真结果证明了IPSO-MPC算法对基于MPC理论的智能车纵向速度控制问题是有效的。
[1] 李国勇.智能预测控制及其Matlab实现[M].2版.北京:电子工业出版社,2010:255-268.
[2] 余胜威.Matlab车辆工程应用实战[M].北京:清华大学出版社,2014:392-395.
[3] 李明喜,章永进,彭永胜,等.车间运动学模型在智能车速度跟踪控制中的应用[J].军事交通学院学报,2015,17(11):49-53.
[4] 罗犇.基于FPGA的预测控制算法并行加速研究[D].杭州:浙江大学,2011.
[5] 张俊溪,张嘉桐,张玉梅.一种改进的粒子群优化算法[J].陕西师范大学学报(自然科学版), 2016(2):15-20.
[6] 谢承旺,邹秀芬,夏学文,等.一种多策略融合的多目标粒子群优化算法[J].电子学报,2015(8):1538-1544.
[7] 黄太安,生佳根,徐红洋,等.一种改进的简化粒子群算法[J]. 计算机仿真, 2013, 30(2):327-330.
[8] 周晶晶,徐友春,李明喜.基于改进的QP算法和MPC理论的智能车纵向速度控制研究[J].军事交通学院学报.2016,18(10):49-53.
[9] 高飞.Matlab智能算法超级学习手册[M].北京:人民邮电出版社,2014:225-226.
[10] 董娜,陈增强,孙青林,等.基于粒子群优化的有约束模型预测控制器[J].控制理论与应用,2009,26(9):965-969.
[11] 罗犇,邵之江,徐祖华,等.一种新的基于PSO的MPC及其硬件实现[J].控制工程,2013,20(2):227-230.
(编辑:张峰)
Application of IPSO-MPC Algorithm in Longitudinal Velocity Control of Intelligent Vehicle
ZHOU Jingjing1, XU Youchun2, ZHANG Zili1, LI Mingxi2, SU Zhiyuan3
(1.Transportation Service Department, Bengbu Automobile NCO Academy, Bengbu 233011, China;2.Military Vehicle Department, Military Transportation University, Tianjin 300161, China;3.Postgraduate Training Brigade, Military Transportation University, Tianjin 300161, China)
The problem of longitudinal velocity control of intelligent vehicle based on model predictive control(MPC) theory can be converted to quadratic programming(QP). Considering this QP problem, an improved particle swarm optimization(IPSO) algorithm is applied to reduce MPC computational cost. In this paper, shrinkage factor is introduced to guarantee particle swarm algorithm convergence, the inertia factor is introduced to avoid the particle oscillating around the global optimal solution, and “spare tire mechanism” is introduced to deal with QP constraint. Numerical experiments show that the improved IPSO algorithm can reduce iterations and computational cost. IPSO-MPC algorithm is formed of IPSO algorithm and MPC algorithm, and the simulation result of intelligent vehicle longitudinal velocity control verified its effctiveness.
longitudinal speed control; intelligent vehicle; particle swarm optimization(PSO); model predictive control(MPC)
2016-10-25;
2016-11-28.
国家自然科学基金项目(91220301);国家重点基础研究发展计划项目(2016YFB0100903).
周晶晶(1986—),男,硕士.
10.16807/j.cnki.12-1372/e.2017.04.010
TP273
A
1674-2192(2017)04- 0038- 05

