基于系统动力学的自然灾害破坏条件下交通设施抢修
张 娜,赵海川,杨殷豪,刘锡鑫
(1.军事交通学院 国防交通系,天津300161; 2.93056部队,辽宁 鞍山 114225;3.西南大学 工程技术学院,重庆 400715)
● 国防交通 National Defense Traffic
基于系统动力学的自然灾害破坏条件下交通设施抢修
张 娜1,赵海川2,杨殷豪3,刘锡鑫1
(1.军事交通学院 国防交通系,天津300161; 2.93056部队,辽宁 鞍山 114225;3.西南大学 工程技术学院,重庆 400715)
为提高自然灾害破坏条件下交通设施抢修速率,保障交通线畅通无阻,基于系统动力学模型,分析影响自然灾害破坏条件下交通设施抢修的诸多因素,建立整个交通设施抢修的系统动力学模型。以地震破坏下交通设施抢修为例,进行模型验证,分析不同决策条件下对抢修队伍在途数量、抢修道路桥梁设施恢复数量等因素的影响,提出加强应急救援保障理论研究、充分发挥基础设施保障效能、提高应急救援快速保障能力的对策与建议。
交通设施抢修;系统动力学模型;自然灾害
我国幅员辽阔,地理、地质、气候条件复杂,直接导致自然灾害种类繁多且发生频繁。据相关数据统计,一般年份,全国受灾人口2亿人(次),因灾死亡数千人,直接经济损失从20世纪80年代的700多亿元增长到近年来的1 300多亿元。灾害发生后,当地政府、军队联合启动应急救援保障机制,“灾情就是命令,时间就是生命”,交通设施的破坏,直接影响应急救援工作的开展。因此,研究自然灾害破坏交通设施的抢修,具有十分重要的意义。
目前,许多学者对自然灾害破坏交通设施抢修的组织机制和技术进行了相关研究。文献[1]针对救灾行动应急交通保障能力,提出了配强应急交通保障装备、拟制救灾行动应急交通保障预案方案、加强交通基础设施建设等对策;文献[2]针对高速铁路桥梁遭受自然灾害损毁的情况,本着预有准备、多案并举、安全快速的原则,对灾后高铁桥梁应急抢修与恢复技术进行了探讨;文献[3]针对中小型混凝土桥梁路基的破坏形式,提出了早强型组合结构技术和快速稳定的路基回填集料技术。本文利用系统动力学理论,提出了一种自然灾害破坏交通设施抢修系统动力学模型,并对模型进行了评价,验证了模型的可靠性,提出了提高交通设施抢修速率的对策。
1 交通设施抢修系统动力学模型分析
1.1 系统动力学基本理论
系统动力学(system dynamics, SD)是由美国教授Forrester在1956年提出的,其最初的目标是为了解决企业生产与库存方面的问题,现已广泛应用于项目管理、学习型组织、公司战略等方面的系统研究[4]。它是以现实的客观存在为对象,根据系统的实际信息构建动态的仿真模型,并通过计算机的反复模拟对系统未来趋势进行分析与研究[5]。系统动力学模型分析流程如图1所示。

图1 系统动力学模型分析流程
1.2 问题描述与模型分析
关于自然灾害交通设施抢修研究可以描述为:灾害发生后,交通设施会受到严重损坏,使得抢修队伍和抢修物资由于交通阻塞不能及时到达受灾一线,而原来驻扎在受灾区的部队、专业保障队伍及战储交通抢修物资对受灾区前期的交通设施修复起着关键的作用。在进行派遣抢修队伍数量和调遣抢修物资时,不仅需要考虑灾区交通设施受损的数量及受损程度,还需要考虑灾区道路的运输能力、修复能力、抢修队伍调度数量及抢修物资数量的情况。
综上所述,交通设施的恢复速率与抢修队伍的数量和所需救援物资成正反馈关系。因此,自然灾害交通设施抢修的关键就是在最短时间内将交通线抢通。抢修队伍决策的制订需要综合考虑灾区交通设施的损坏情况、道路运输的路况、所需要抢修的数量等多种因素;抢修物资数量的决策制订需考虑灾区交通设施修复的需求量、道路运输的路况等一系列因素。因此,本文通过抢修队伍配置、道路的实际运输能力、抢修物资需求3个模块,建立了自然灾害破坏交通设施抢修的系统动力学模型,并分析了不同决策情况下的应急抢修效果。
2 交通设施抢修系统动力学模型流图和方程
2.1 交通设施抢修流图
根据系统动力学的建模流程,建立自然灾害破坏条件下交通设施抢修系统动力学模型流图(如图2所示)。
2.2 系统动力学方程
(1)抢修队伍模块主要系统方程。
CLP=β×PULSE(tc,0)
ZYP=IF THEN ELSE(ZSP>DYA,DYA,ZSP)
ZSP=INTEG(IF THEN ELSE(ZTP≥0,ZYP-DBP,0),0)
ΔRSP=(DBP+ZBP)×RS
N=DBP+ZBP-RSP
式中:CLP为出发人数;ZYP为道路在运人数;ZSP为被阻塞部队人数;ZTP为在途部队人数;DBP为到达灾区救援部队人数;ZBP为灾区驻守部队人数;N为抢修队伍数量;RSP为累计受伤人员数;

图2 交通设施抢修系统动力学模型
ΔRSP为受伤增加人数;RS为受伤率;β为救援部队投入决策因子;tc为决策延迟时间。
(2)抢修物资模块主要系统方程。
RFH=IF THEN ELSE (ZS>DYA,0,MAX(δ,0)/tt)
ZYW=IF THEN ELSE(ZSW>DYA,DYA,ZSW)
KCL=INTEG(RWD-RWX,CSL)
δ=MAX(JCL-ZYW,0)
ZXL=ZXLper×N式中:RFH为物资发货率;ZS为阻塞水平;DYA为道路运输能力;ZYW为在运物资量;ZSW为被阻塞物资量;JCL为灾区决策者订单量;ZXL为灾区需求量;ZXLper为灾区个体需求量;RWD为物资抵达速率;RWX为物资消耗速率;KCL为受灾区域抢修物资库存量;CSL为受灾区域抢修物资初始库存量;δ为补货决策因子;tt为库存调节时间。
(3)道路运输能力抢修模块主要系统方程。
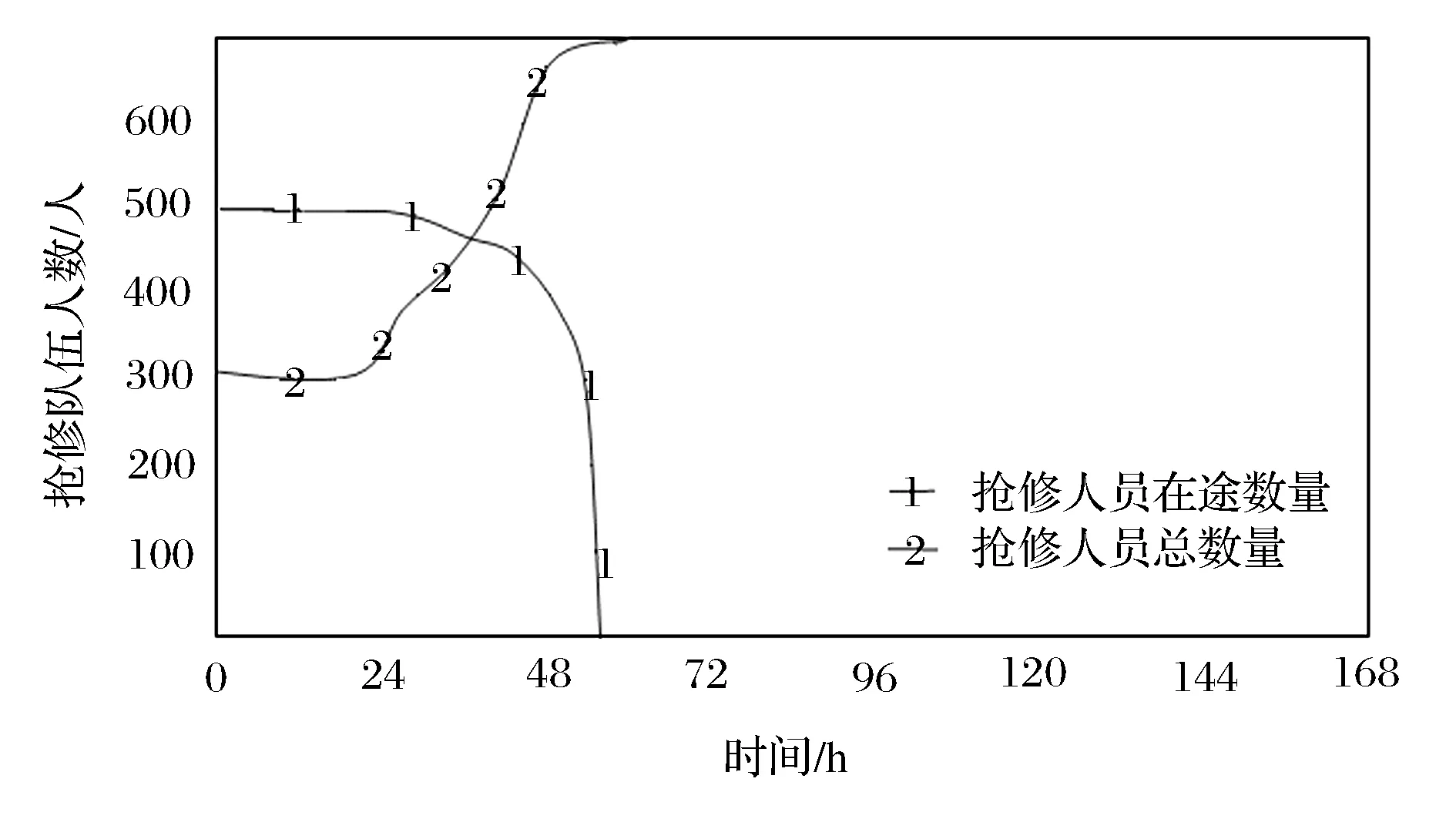
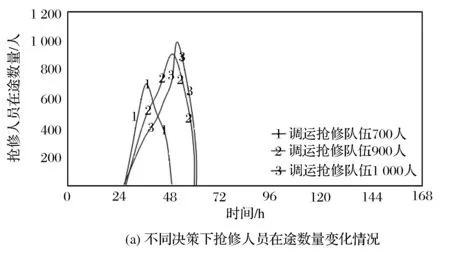
RDH=IF THEN ELSE(χ DSL=RDS×DL DXL=INTEG(RDH,0) RDS=(RYS+RCS)×α DYA=WZA(1-Ra) 式中:RDS为道路桥梁设施损坏率;RDH为道路桥梁设施恢复率;DSL为道路桥梁设施损坏数量;DXL为累计抢修道路桥梁设施数量;DL为抢修区域道路桥梁总量;χ为道路桥梁设施抗灾系数;RYS为原生灾害破坏率;RCS为次生灾害破坏率;α为山区因子;DYA为道路运输能力;WZA为无灾情况道路运输能力;Ra为通道运输能力减小率。 本文拟选取自然灾害中对交通设施破坏较严重的地震灾害,模拟预测地震灾害发生后交通设施的抢修,以验证模型的可靠性,并分析不同的政府和部队决策投入抢修队伍力量的多少、物资调运的配置等对交通设施抢修效果的影响。 3.1 模型参数设置与验证 当自然灾害发生时,灾害发生的类型、等级、时间、地点等条件的不同,对交通设施抢修的参数输入也不尽相同,需依据实际情况进行参数设置与输入。本文以1 h为时间步长进行模拟,仿真周期为168个周期,即7天。选取地震对交通设施破坏较大的震级,对应等级为8级,一般交通设施抗灾系数能达到6级,人均抢修能力0.2 m/h,抢修队伍受伤率为0.005 人/h,在未发生自然破坏的情况下,道路的运输能力能够达到100 人/h,物资能够达到100 件/h。假设选取受灾区域原驻守部队人员300人,灾害发生后第一时间决策投入500人,抢修物资的调运时间一般为12 h,库存调节时间24 h,假设初始的抢修物资的库存量为100件。 根据初始参数设置和运行系统,选取道路运输能力、抢修队伍的在途与到达、抢修物资的调运与到达等具有代表性的变化指标,分别用系统仿真结果的数据变化图进行表示。 图3所示为道路运输能力随时间变化的仿真效果。在灾害发生前期,由于道路、桥梁等受到原生灾害的影响,处于断通状态,道路运输能力从无灾状况迅速下降,有可能直接降到零的状态,而后随着抢修的进行,其逐渐恢复,又由于有次生灾害的发生,其中间有波动状态。 图3 道路运输能力随时间变化仿真效果 图4所示为抢修队伍数量变化仿真效果。由曲线1可以看出,前期由于道路运输能力的逐步减小,人员运输会受到阻塞,随着抢修队伍的抢修,道路运输能力将逐渐恢复,人员受阻现象将逐渐解除;由曲线2可以看出,前期抢修队伍由灾区原有抢修队伍组成,等到道路恢复到一定程度,调运抢修队伍才能进入灾区,又由于道路运输能力恢复到一定程度达到最大,则进入灾区的抢修队伍在61 h后就基本处于稳定状态。 图4 抢修队伍数量变化仿真效果 图5所示为抢修物资数量变化仿真效果。由曲线1可以看出,需求量随着受灾后的道路、桥梁等设施的破坏情况,在短期内呈现稳定状态,随着消息送达抢修队伍,统计数据将呈现短暂的上升,随后趋于稳定;由曲线2可以看出,前期由于道路破坏的影响,在短期内器材供应呈现零到达的状况,随着道路运输能力的逐步提高,器材逐步到达,之后趋于稳定。 图5 抢修物资数量变化仿真效果 3.2 不同决策的仿真结果分析 图6所示为不同决策下抢修队伍与道路桥梁设施恢复随时间变化仿真效果。由图6可以看出,在调运抢修队伍不同数量时,当调运抢修队伍数量超过道路运输能力时,抢修队伍在途数量在一定时间内保持不变,也就是出现道路阻塞现象,调运过多的抢修队伍会使得在途人员数量和在途时间明显增长,致使交通设施抢修时间延长;随着调运抢修队伍数量增多,抢修道路桥梁设施恢复数量相同时,会节省很多时间。 图6 不同决策下抢修队伍与道路桥梁设施恢复随时间变化 仿真效果 (1)基于体系建设思想,加强应急救援保障理论研究。自然灾害突发性强,时间、地点、规模、破坏程度等具有不确定性。而应急救援交通保障涉及政府、军队等多个部门,需发挥军民融合、军地一体的系统优势,加强军队、政府等多个部门的统一领导,加强应急救援保障理论研究,快速组织地方专业保障队伍、部队抢修力量,综合运用各种交通抢修技术手段,快速展开交通线的抢修。 (2)完善军民联动机制,充分发挥基础设施保障效能。应对自然灾害时,启动应急保障机制是应急救援行动的共同特点。完善军民联动机制、制订合理的应急交通保障预案,需建立军地一体的交通运输指挥机构,对多种运输方式实施综合、立体的管控,强化对重点交通线路、交通枢纽等重要目标进行全方位管控、疏导,防止线路拥堵、秩序混乱,以确保救援队伍和物资的快速到位。 (3)优化器材储备布局,提高应急救援快速保障能力。交通抢修物资是抢修保通的关键因素之一。交通抢修物资作为交通战备储备物资,应根据不同地区的道路、桥梁等交通设施的统计数据,在影响应急救援的主交通要道、主交通网路、主交通节点等领域,优先建立交通抢修物资仓库,为交通设施抢修抢建提供充足的保障,以提高快速应急救援能力。 本文将系统动力学模型应用到自然灾害破坏交通设施抢修的系统中,提出了一种自然灾害破坏条件下交通设施抢修的SD模型。结合应急抢修实际现状,分析了影响交通设施抢修的诸多因素,建立了系统动力学模型,并通过初始数据设置验证了该模型的可靠性,模拟分析了不同决策情况下交通设施的抢修效果,并针对模型仿真结果提出了加强应急救援交通保障体系建设、制订合理的应急救援交通保障预案和合理规划交通抢修物资储备仓库布局的对策与建议,对于政府和部队提高自然灾害破坏下交通设施抢修的效率,具有参考价值。 [1] 刘勇,李爱武.着力加强救灾行动应急交通保障能力建设[J].后勤学术,2009(6):27-29. [2] 张耀辉,王海林,秦志宇.高铁桥梁灾后应急抢修与恢复技术探讨[J].国防交通工程与技术,2015(6):31-35. [3] 韦灼彬,刘晶晶.交通基础设施应急抢修技术研究[J].海军后勤学报,2007(3):40-42. [4] 王琪.基于系统动力学的地震应急资源配置模型研究[D].大连:大连理工大学,2013. [5] 李健,张文文,白晓昀,等.基于系统动力学的应急物资调运速度影响因素研究[J].系统工程理论与实践,2015(3):661-668. (编辑:张硕) Traffic Facility Repair Under Condition of Natural Disaster Damage Based on System Dynamics ZHANG Na1, ZHAO Haichuan2, YANG Yinhao3, LIU Xixin1 (1.National Defense Traffic Department, Military Transportation University, Tianjin 300161,China; 2.Unit 93056,Anshan 114225, China; 3.College of Engineering and Technology, Southwest University, Chongqing 400715, China) s: To improve the rate of traffic facility repair under condition of natural disaster damage and to keep traffic line unimpeded, the paper firstly analyzes many influencing factors in traffic facility repair under condition of natural disaster damage based on system dynamics, Then, it establishes system dynamics model of the whole traffic facility. Finally, it verifies the model with traffic facility repair under earthquake damage and analyzes the impact of different decision conditions on repair personnel transiting quantity and restoring road and bridge facilities, and puts forward countermeasures on strengthening theory study of emergency rescue support, making full use of infrastructure support, and improving rapid support capability of emergency rescue. traffic facility repair; system dynamics model; natural disaster 2016-11-05; 2017-01-20. 张 娜(1984—),女,硕士 ,讲师. 10.16807/j.cnki.12-1372/e.2017.04.004 E951.3 A 1674-2192(2017)04- 0013- 053 交通设施抢修模型参数设置与仿真结果分析



4 交通设施抢修的对策与建议
5 结 语

