无人机地面运动控制与仿真

王 茜,孙 科

(中国飞行试验研究院，西安 710089)

无人机地面运动控制与仿真

王 茜,孙 科

(中国飞行试验研究院，西安 710089)

为了解决无人机纠偏刹车系统中实际存在的问题，对无人机地面运动进行了研究，采用前轮转弯、方向舵、差动刹车联合使用模式，以无人机的侧偏角、侧偏距为反馈信号，设计了无人机地面运动纠偏控制律，通过遗传算法的全局优化过程实现其纠偏参数寻优，在Simulink平台建立了无人机纠偏数学模型；试验结果表明，建立的无人机地面运动纠偏数学模型正确有效，能够模拟出无人机地面运动的真实情况；基于遗传算法的控制策略能够实现一定范围内的无人机地面运动纠偏，提高跑道的利用率。

无人机；仿真；纠偏控制；遗传算法

0 引言

无人机地面运动是无人机安全起降过程的一个重要阶段，通过对无人机地面运动的研究，对实现起降过程的自动控制有着重大的意义。目前国内对于无人机的地面运动研究相对较少，只有少部分无人机能够实现全自主起飞着陆。对无人机六自由度地面运动，特别是偏航和侧向运动的研究不足，还有很多工作需要去做。文献[1]分别使用了前轮转向与主轮差动两种方式进行纠偏，对比了两种纠偏方式的纠偏效果；文献[2]使用了主轮刹车与方向舵联合仿真纠偏；文献[3]使用了主轮刹车、前轮转弯以及方向舵联合仿真，但在这些文献中，在给出纠偏控制参数时，都是直接给出固定参数值，没有统一给出纠偏参数寻优的方法。

本文针对以上问题，在MATLAB中的Simulink平台中建立了无人机机体模型、机轮模型、起落架模型、跑道/机轮摩擦系数模型、刹车系统作动装置模型以及刹车装置模型；在此基础上，使用了主轮刹车、前轮转弯以及方向舵联合纠偏控制律，并且采用了遗传算法设计其控制参数，对无人机的地面运动进行仿真分析。对改进、设计新型高性能控制律，提高无人机着陆阶段的安全性能具有很大的借鉴意义。

1 无人机地面运动模型建立

1.1 质心运动学方程

在惯性地面坐标系下，应用牛顿第二定律建立无人机在合外力F作用下的线运动，得到质心运动方程组如下所示：

(1)

式中,∑Fx、∑Fy、∑Fz分别是机体坐标下的3个轴的合力；m为无人机的质量；u、v、ω为无人机沿机体轴的3个线速度；p、q、r为无人机沿机体轴的3个角速度。

1.2 质心转动动力学方程

根据牛顿第二定律建立无人机在外和力矩∑M作用，得到角运动方程组如下所示：

(2)

式中,∑Mx、∑My、∑Mz分别是机体坐标系下3个轴的合力距；Ix、Iy、Iz、Ixz分别为航向方向转动惯量、翼展方向转动惯量、垂直方向转动惯量、航向与垂直方向转动惯量。

1.3 无人机地面运动受力分析

在考虑无人机的受力时，必须考虑起落架与地面的相互作用，无人机的受力分析图如图1所示，G为重力；T为发动机慢车推力；Fs为伞阻力；Y为空气升力；X为空气阻力；Z为空气侧力；Fxi，Fyi，Fzi分别为纵向摩擦力，侧向摩擦力以及支持力，i=1，2，3分别为前轮，左主轮，右主轮。

图1 无人机地面运动受力分析

1.3.1 重力

无人机重力G的分量为[00mg]T。

1.3.2 气动力

阻力：

X=0.5CxρsV2

(3)

侧力：

Y=0.5CyρsV2

(4)

升力：

Z=0.5CzρsV2

(5)

式中,Cx、Cy、Cz为气动系数，在机体坐标系下的值；Cl、Cm、Cn为力矩系数，在机体坐标系下的值；ρ为空气密度；s为机翼面积。

1.3.3 发动机推力

在机体坐标系中，发动机推力矢量表示为：

T=[Tcosφp-Tsinφp]T

(6)

1.3.4 地面对无人机的作用力

地面对无人机的作用力主要是由地面对轮胎产生的纵向摩擦力，侧向摩擦力，以及起落架对无人机的垂直方向的支撑力。

1.3.4.1 起落架支反力

起落架的压缩力为:

(7)

式中，K1为弹簧系数；K2为阻尼系数；ΔZ为起落架位移变化量。

1.3.4.2 轮胎/跑道摩擦力

刹车制动时主要依靠轮胎与地面产生摩擦力来刹停，跑道与轮胎的摩擦系数不是一个常量，它受很多因素的影响，例如无人机速度、滑移率、无人机载荷、轮胎侧倾角、跑道状况等等复杂因素。

跑道对轮胎的摩擦力可以分为纵向及侧向两个方向来考虑。

FX=FZ*μX

FY=FZ*μY

(8)

2 无人机与地面摩擦系数的求取

2.1 总摩擦系数

根据相关资料可以知道，跑道给机轮提供的摩擦系数存在一个最大值，这个最大值与跑道的状况，无人机速度以及轮胎的充气压力有关，如下表示：

干燥路面：

μmax=0.912(1-0.0011p)-0.00079V

(9)

潮湿路面：

(10)

结冰路面：

(11)

式中,p为轮胎充气压力；V为无人机速度。

在这里，我们定义轮胎的滑移率为：

(12)

式中,Δx=Vtcosβ-x，Δy=Vtsinβ；δx，δy分别为轮胎的纵向及侧向滑移率；x，y分别为轮胎的纵向及侧向位移；β为轮胎的侧滑角。

为了更好的表示与理解，定义轮胎的广义滑移率为：

(13)

式中，Φ，Φx，Φy为轮胎总体侧向及纵向的广义滑移率；Nx，Ny为轮胎的刚度系数；μx，μy为轮胎的纵向及侧向摩擦系数；Fz为轮胎的垂直载荷。

如图2所示，根据摩擦椭圆假设[5]，我们可以得到，无人机的纵向摩擦系数最大值及侧向摩擦系数最大值满足:

(14)

再根据受力分析，通过合理的简化可以近似得到，无人机的纵向摩擦系数最大值及侧向摩擦系数最大值满足：

(15)

并且：

(16)

式中,μxmax，μymax分别为轮胎纵向与侧向的摩擦系数的最大值。

2.2 纵向摩擦系数

准稳态模型中，最著名同时也是最典型的模型就是Pacejka模型，也叫“魔术公式”[6]，由于该模型能够狠好的匹配实验数据，因此本文使用该模型模拟计算轮胎与跑道间的纵向摩擦系数，具体表达式如下：

μx=B1sin(B2arctan(B3σ))

(17)

式中,B1为峰值因子，B1=μxmax；B2为刚度因子；B3为曲线因子。

在不同跑道状态下，实验测得的B2，B3的取值分别为：

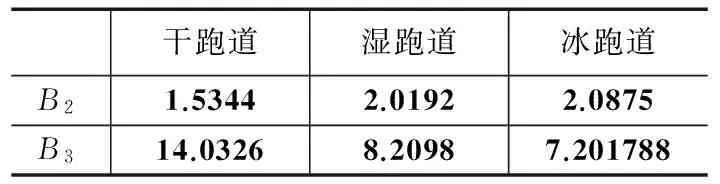
表1 不同跑道状态B2，B3的取值

2.3 侧向摩擦系数

侧向摩擦系数与轮胎的侧向刚度、垂直载荷，轮胎侧偏角的因素[36]有关， 左主轮的侧偏角为：

(18)

右主轮的侧偏角为：

(19)

前轮可以相对机体偏转，前轮的侧偏角为：

(20)

式中，am，an，bw为左右主轮及前轮到重心的水平距离及纵向距离；r为无人机的偏航角速度；θL为给定控制是无人机速度在机体坐标系的分量；[ugvgwg]为无人机速度在稳定坐标系中的分量。

根据上面求得的侧偏角和广义滑移率，轮胎/跑道的摩擦系数为：

(21)

(22)

(23)

式中,p为轮胎充气压力；Pr为轮胎额定充气压力；w为轮胎宽度；d为轮胎直径；δ为轮胎压缩量；Cc为转弯刚度系数。

Cc的取值如表2所示。

3 纠偏控制律设计

无人机实时输出横侧向的运动信息，输入传动刹车控制律通道中，经过一定的运算分析，产生差动刹车指令，传给相应的刹车机构，刹车机构产生刹车量，控制无人机的侧偏距和侧偏角保持在一定的范围内。

侧偏距为主反馈信号，同时引入侧偏速度、偏航角、偏航角速度信号以改变纠偏控制性能。这些信号被送入刹车纠偏控制律模块，刹车纠偏模块产生刹车指令，刹车控制器根据刹车指令给出左右刹车机构不同的纠偏刹车量，刹车机构叠加纠偏刹车量和刹车量，将叠加后的刹车信号送给电控刹车阀，对无人机产生左偏或右偏控制作用。

δb=ky(y-y0)+kvyvy+kψ(ψ-ψ0)+krr

(24)

若δb≥0，δbr=δbt，δbl=δbc+δbt；

若δb≤0，δbl=δbt，δbr=δbt-δbc。

当无人机速度达到某一值后且偏离跑道中心线，此时纠偏和刹车两种状同时存在，首先飞控会根据速度的不同给出不同的刹车量，若果此时机轮偏离跑道中心线，刹车控制器也会给出相应的纠偏刹车量，最后将刹车量和纠偏刹车量叠加，送给刹车机构，实现刹车、纠偏、再刹车的循环状态。

在无人机地面运动时，当已经产生了一定的侧偏距，对其进行纠正时，要求系统的响应满足以下条件：

1)系统能平稳快速的回到跑道中心线；

2)在纠偏过程中，最大的侧偏距不能超过给定的范围。

按照这个要求，规定该系统的响应时间不超过10s，最大的侧偏距不超过10m。

(25)

式中,Dzm为纠偏参考模型输出；Dzc为侧偏指令；ωn为二阶环节自然频率；ξ为相对阻尼比。

适应值函数为：

(26)

式中,Dzm(i)为iT时刻参考模型的侧偏距输出值；Dz(i)为iT时刻无人机的侧偏距；T为数据值解算的步长；N为总解算时间对应的解算总步数。

4 仿真结果分析

无人机在干跑道着陆时就存在10m的初始侧偏距进行纠偏刹车的仿真曲线如图2～9所示。由仿真图可以观察到，无人机在干跑道10m纠偏时的刹车距离为390m，刹车时间为19s。与无初始侧偏距的情况进行刹车的情况相对比，刹车距离增加，刹车时间变长。产生这种情况的原因主要有两点：第一点是侧偏距的存在，使得无人机滑跑的轨迹由直线变为曲线；第二点是由纠偏策略决定的，无人机在着陆滑跑时，在制动的同时还需要纠偏。在制动时，需要设定一个刹车量的标准值，左主轮与右主轮都按照这个刹车百分比的刹车压力来刹车，在纠偏时，需要降低某个主轮的压力达到纠偏的目的。比如无人机在跑道中心线的右侧，欲使无人机回到跑道中心线需要其机头向左偏转，在这个过程中，左轮的刹车压力不变，右轮的刹车压力降低，右机轮速度变快，它与地面的结合力降低，左右轮与地面结合力的差距产生了向左的偏航力矩，最终实现纠偏的目的。整个纠偏过程中中，由于刹车压力是在预置压力的基础上减少，故从总体上来看刹车压力减小，刹车距离变长，刹停时间也变长。

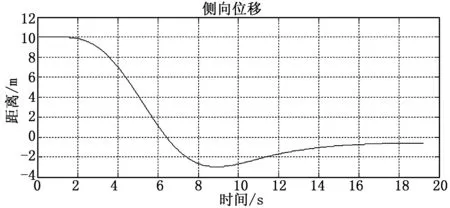
图2 侧向位移变化

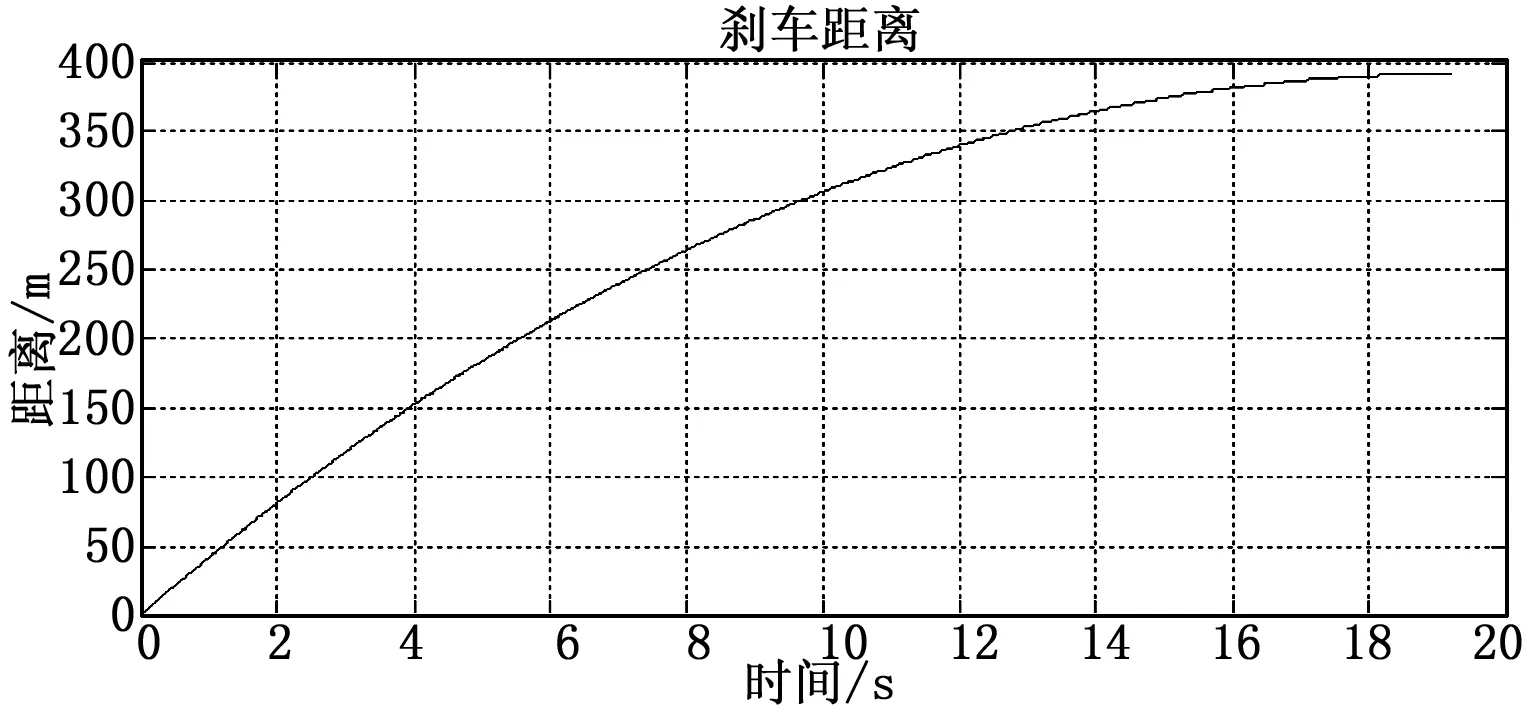
图3 刹车距离变化

图4 无人机高度变化

图5 无人机滚转角变化

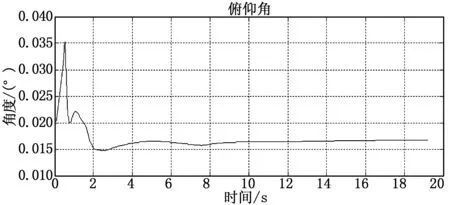
图6 无人机俯仰角变化

图7 无人机偏航角变化

图8 无人机速度及机轮速度

图9 刹车压力变化

从仿真结果还可以看到，侧偏距由初始的10m平稳的减小，经过一个较小的震荡后，保持在0附近。滚转角在一个极小的领域内震荡并趋于稳定，基本保持在0°，故机身不会发生很大的滚转运动，造成无人机的事故。偏航角初始时由于无人机机头向左偏转，故有一个很小的负角度，后来逐渐调整，最终也恢复到0°附近。这说明了在干跑道滑跑时，对于10m的初始侧偏距，具有非常良好的纠偏效果。

5 结束语

考虑无人机在地面运动时左右轮受力不一致的情况，在Matlab/simulink仿真平台下，建立了六自由度模型模型。并通过为设计刹车控制律，解决了主轮载荷不同时可能会出现的侧滑等安全问题，提高了飞机地面运动的稳定性和安全性。仿真结果证明模型有效，控制算法可行。

[1] 陈 磊. 飞翼飞行平台地面滑跑建模与航迹纠偏控制研究[D]. 南京：南京航空航天大学, 2009.

[2] 张华亮, 周 洲. 飞翼无人机地面滑跑建模与航向控制[J]. 系统仿真学报, 2009, 20(24): 6759-6762.

[3] 周乃恩. 无人机起降纠偏控制技术研究[D]. 哈尔滨：哈尔滨工程大学, 2011.

[4]BaarspulM.AReviewofFlightSimulationTechniques[J].ProgressintheAerospaceSciences(S0376-0421), 1990, 27(1): 1-120.

[5]GuoKH.Aunifiedtiremodelforbrakingdrivingandsteeringsimulation[R].SAETechnicalPaper, 1989.

[6]CabreraJA,OrtizA,CarabiasE,etal.Analternativemethodtodeterminethemagictiremodelparametersusinggeneticalgorithms[J].VehicleSystemDynamics, 2004, 41(2): 109-127.

[7]SmileyRF,HorneWB.Mechanicalpropertiesofpneumatictireswithspecialreferencetomodernaircrafttires[J].Tires，1958.

Simulate and Control of Unmanned Aerial Vehicle’s Ground Moving

Wang Qian,Sun Ke
( Flight test establishment of China, Xi’an 710089,China)

In order to solve the actual problems arose with the lateral deviation braking system, a mathematical model of lateral deviation control of Unmanned Aerial Vehicle was built on Simulink, the correction algorithm of Unmanned Aerial Vehicle moving on the ground was designed and its correction parameter was programmed to the best by the front wheel steering, the nose wheel string, the difference in combined brake model and the rudder to control the lateral deviation correction, and also by the application of the full optimization process of genetic algorithms. By applying the control method of genetic algorithms, it is possible to achieve certain level of deviation correction in the Unmanned Aerial Vehicle’s moving on the ground and can thus improve the utilization of runways.

unmanned aerial vehicle;simulation; lateral deviation control; genetic algorithms

2017-01-05；

2017-01-20。

王 茜(1990-)，女，陕西延安人，硕士研究生，助理工程师，主要从事机载测试方向的研究。

1671-4598(2017)04-0087-04

10.16526/j.cnki.11-4762/tp.2017.04.025

TP27

A