基于PRI的雷达信号综合分选方法

魏可友，黄 康，梁 广，刘会杰

（1.中科院上海微系统与信息技术研究所 上海200050；2.上海微小卫星工程中心 上海201203）

基于PRI的雷达信号综合分选方法

魏可友1，2，黄 康2，梁 广2，刘会杰2

（1.中科院上海微系统与信息技术研究所 上海200050；2.上海微小卫星工程中心 上海201203）

针对常规雷达信号和复杂雷达信号同时存在的复杂信号环境，以及减少混合脉冲序列的分选时间，基于PRI变换提出一种PRI变换法及其改进方法相结合的综合分选方法。仿真验证，该方法可行，并对脉冲丢失严重的情况仍具有很好的分选效果。

信号分选；PRI变换；综合分选方法；脉冲丢失

雷达信号分选是雷达对抗的关键技术，通过雷达信号分选，准确识别出空间中各种不同的雷达及其参数，并将其放入雷达库中以便后续的定位、跟踪、干扰等处理。利用脉冲重复间隔（PRI）的重频分选方法是主分选中主要使用的方法。随着辐射源数及雷达脉冲信号形式的不断增多，在接收到的混叠脉冲流中，往往同时存在常规雷达信号、复杂雷达信号（PRI服从某种调制规律）以及脉冲丢失。为了保证对混叠脉冲流分选的实时性和高效性，将PRI变换法及其改进方法结合起来，可以实现准确分选。

1 序列检索

基于PRI的所有分选算法都由PRI估计和序列检索两个过程组成。序列检索是根据正确估计的PRI值，将该部雷达的全部脉冲从交叠的脉冲流中全部分离出来。脉冲列检索是所有雷达信号分选方法都必须包含的重要一步，检索性能的好坏直接影响分选脉冲的有效性。文中使用直接序列搜索，根据已经估计得到的PRI值，将脉冲间隔为PRI或者PRI的整数倍的脉冲信号从脉冲流中分离出来。

直接序列搜索的步骤如下：首先，程序将第一个脉冲作为基准脉冲，然后搜索下一个脉冲，判断两个脉冲之间的TOA差值（即）是否大于某个规定值（该值为PRImax），如果大于该值，则表明所选基准脉冲不在此PRI的脉冲列，以下一个脉冲为基准脉冲继续进行前面的过程。若不大于该值，判断两个脉冲之间的TOA差值（即）与 PRI的比值是否在设定的容差范围（容差即为脉冲抖动量）内，如果超出容差范围，则进行后一脉冲的比较过程。如果与PRI的比值是在设定的容差范围内，则将基准脉冲和该脉冲分离出来，并继续下一脉冲与基准脉冲的比较。将后续脉冲依次与此基准脉冲比较，直至分离结束。判断以此PRI值进行序列搜索出的脉冲数，如果脉冲数大于某个规定值，则搜索成功，否则，搜索失败，以估计出的下一个PRI值进行搜索。

2 基于PRI变换的分选方法

2.1 PRI变换法

设用脉冲前沿时间表示脉冲的到达时间，令tn（n=0，1，2，…，n-1）为脉冲的到达时间，其中n是采样脉冲数。若只考虑使用TOA这个参数，则采样脉冲串就可以模型化为单位冲击函数的和，可表示为

的积分变换公式为：

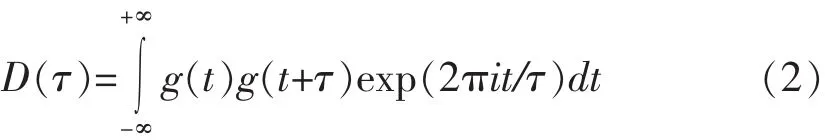
式中，τ＞0。式（2）即为PRI变换，它给出一种PRI的谱图，在代表真PRI值得地方将出现峰值。将（1）代入（2）得到：

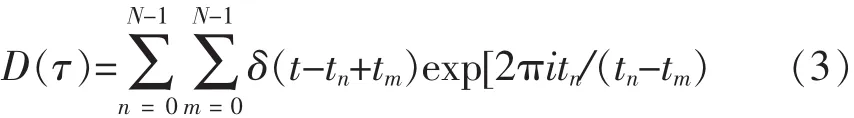
设[τmin，τmax]为PRI的取值范围，将其分成K个小区间（即PRI箱），每个PRI箱的宽度为b=（τmaxτmin）/K，则第 k个 PRI箱的中心为 τk=[（k-1/2）/K]（τmax-τmin）+τmin，k=1，2，…，K。在式（3）的基础上进行PRI取值统计

|Dk|为PRI值统计脉冲数。超过门限时其对应的PRI值即为可能的PRI值。

在PRI变换中，由于相位因子exp（2πitn/τ）或exp[2πit/（tn-tm）]的引入，几乎完全抑制了出现在自相关函数中的子谐波。在直方图分选方法中由于脉冲丢失引起的谐波问题，使用PRI变换可以得到解决。因此，PRI变化在脉冲丢失严重的情况下仍然有很好的分选效果。另外，PRI变换分选是直接由PRI变换估计出PRI值之后，根据得到的PRI进行序列检索，直方图类的分选方法（包括CDIF、SDIF）是对每一级直方图中超过门限的PRI值进行序列搜索，在此过程，PRI变换分选可以节省大量搜索时间。

2.2 改进的PRI变换法

PRI变换法对抑制谐波、脉冲丢失有较好的分选效果，但对于脉冲的PRI存在抖动时，用PRI变换法估计PRI值时，真实的PRI被噪声淹没，不能估计出正确的PRI值。如图1，是对含有两个常规雷达（PRI1=170 μs，PRI2=300 μs）的脉冲列进行PRI变换，可以正确估计出脉冲列中两部雷达的PRI值。图2为对这两部雷达脉冲PRI加入10%的抖动量，用PRI变换法进行分选，使用PRI变换后，PRI值完全被噪声淹没。

图1 PRI变换法对常规信号分选图

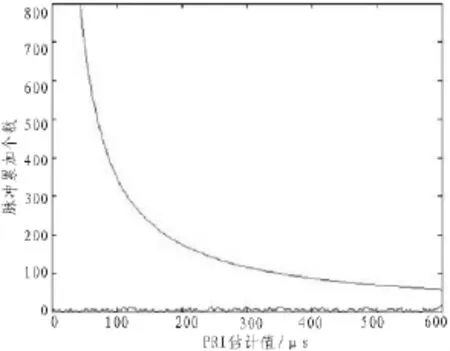
图2 PRI变换法对PRI抖动信号分选图

分析上述情况原因，主要是因为随着脉冲到达时间离起点时间渐远，相位因子exp[2πit/（tn-tm）]的相位误差也随着增大；又由于PRI抖动的影响，使得本该在同一个PRI箱里的脉冲却落在了PRI中心值附近的几个箱中，这使得传统PRI变换法在脉冲存在抖动时，使得真实的PRI值被噪声淹没掉。针对PRI变换法的这两个缺点，对其进行以下两个方面的改进。

1）使用可移动的起始时间点，来减小相位因子的相位差。通过改变时间起点，减小因TOA远离时间起点造成的相位误差，通过不断移动时间起点，相位因子的相位误差不会积累，即可减少相位因子的误差。

2）使用交叠的PRI箱来增加PRI箱的宽度，以此来克服PRI箱宽度和PRI抖动宽度与PRI估计精度之间的矛盾。

改进后的PRI变换法较传统PRI变换法，由于不断移动的时间起点和交叠箱的引入，使得计算量增加，算法复杂度提高，因此分选时间增加。

2.3 基于PRI变换的综合分选方法

1）首先对接收到的脉冲序列利用2.1节中式（4）进行PRI取值统计。

2）对所有|Dk|值超过门限的PRI值依次进行序列检索。将成功搜索到的脉冲序列从原始脉冲流中扣除，剩下的脉冲流中只含有复杂雷达信号脉冲序列。

3）利用改进的PRI变换法对剩余的脉冲进行分选。

4）对改进PRI变换估计出的PRI值进行后续的参差识别和调制识别。

3 仿真分析

假设待分选脉冲流中共有5部雷达：两部常规雷达（PRI1=170 μs，PRI2=230 μs，20%的脉冲丢失）；三部带有一定抖动量的复杂雷达信号 （PRI3=120 μs，PRI4=210 μs，PRI5=300 μs，抖动量为10%）。

接收到的雷达脉冲序列的TOA-PRI效果图，如图3所示，毫无规律。首先，使用传统的PRI变换法对脉冲流进行分选，并搜索出脉冲流中的常规雷达信号。考虑脉冲流密度较高，脉冲丢失严重，将PRI箱数取为300，τmin=0 μs，τmax=1 000 μs，仿真结果如图4所示。

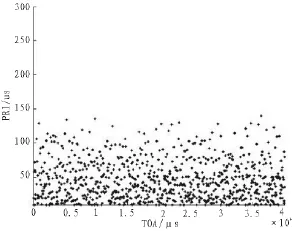
图3 待分选脉冲列TOA-PRI效果图

图4 PRI变换法分选图

从图4可以看出，在含有5部雷达的脉冲流中，使用传统的PRI变化法可以估计出两个PRI值，PRI1=170 μs，PRI2=230 μs，将这两个PRI值用于序列检索，成功搜索出两个脉冲列并将其从脉冲流中扣除，得到剩余脉冲序列的TOA-PRI效果图，如图5所示。然后对剩余的脉冲流进行采用改进的PRI变换法，估计其中可能存在的PRI中心值，结果如图6。从图6中可看出，利用改进的PRI变换法可以很到估计出带有抖动量的 PRI值 （PRI3=120 μs，PRI4=210 μs，PRI5=300 μs）。

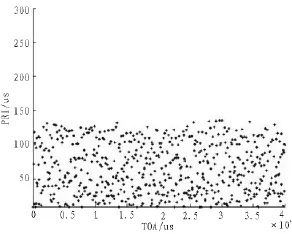
图5 剩余脉冲流TOA-PRI效果图

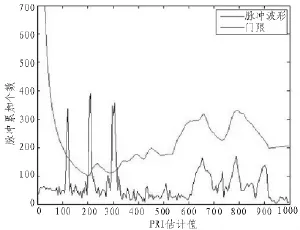
图6 改进的PRI变换法分选图

然后对剩余的脉冲流采用改进的PRI变换法进行分选，估计其中可能存在的PRI中心值，结果如图6。从图6中可看出，利用改进的PRI变换法可以很到估计出带有抖动量的PRI值（PRI3=120 μs，PRI4= 210 μs，PRI5=300 μs）。仿真表明，基于PRI变换的综合分选方法可以很好地对常规雷达信号和复杂雷达信号同时存在的复杂雷达信号进行分选。

4 结束语

文中首先针对常规雷达信号和复杂雷达信号同时存在的复杂雷达信号环境，提出基于PRI变换的综合分选方法，为了减少混合脉冲流的信号分选时间，首先采用传统的PRI变换法从混合脉冲流中分选出常规雷达信号，然后对剩余脉冲流使用改进后的PRI变换法进行分选。仿真结果表明，该算法可行，并对脉冲丢失严重的情况仍具有很好的分选效果。随着雷达辐射源数目不断增加以及信号形式越来越复杂多样，雷达信号分选的高效性、实时性以及抗干扰能力仍需要不断改进。

[1]王杰贵，靳学明.现代雷达信号分选技术综述[J].雷达科学与技术，2006，4（2）：104-108.

[2]熊永坤，时磊，等.一种复杂电磁环境下雷达信号综合分选方法[J].雷达与对抗，2011，31（4）:38-40.

[3]柴娟芳.复杂环境下雷达信号的分选识别技术研究[D].哈尔滨:哈尔滨工程大学，2009.

[4]国强.雷达信号分选理论研究[M].北京:科学出版社，2010，27（3）:50-52.

[5]杨文华，高梅国.基于PRI的雷达脉冲序列分选方法[J].现代雷达，2005，27（3）:50-52.

[6]王海滨，马琦.一种基于PRI变换的雷达信号分选方法[J].现代电子技术，2013，36（1）:28-31.

[7]Milojevic D J，Popovic B M.Improved Algorithm for the Deinterleaving of Radar Pulse[J].IEE Proceedings，Pt F，1992，139（1）：98-104.

[8]Nelson D.J.Special Purpose Correlation Function for Improved Signal Detection and Parameter Estimation.In Proceedings ofInternational Conference on Acoustics.Speech.and Signal Processing（ICASSP）.1993，57（4）:73-76.

[9]Kenichi N，Masacki K.Improved Algorithm for Estimating Pulse Repetition Intervals.IEEE Trans on Aerospace and Electronic Systems.2000，36（2）: 407-421.

[10]王国立，王建华.一种雷达信号综合分选方法研究[J].电子设计工程，2013，21（1）：96-102.

[11]王海滨，马琦.一种基于PRI变换的雷达信号分选方法[J].现代电子技术，2013，36（1）:28-31.

[12]明焱.未知雷达信号PRI分选算法研究 [D].西安：西安电子科技大学，2013.

[13]岳志勇，肖军鹏，王鹏.重频抖动脉冲信号分选研究[J].遥测遥控，2007，28:118-122.

[14]罗长胜，吴华，程嗣怡.一种对重频调制与抖动信号的PRI变换分选新方法 [J].电讯技术，2012，52（9）:1492-1496.

[15]李永红，邱杰，孙文军.一种改进的雷达脉冲信号分选算法[J].中国电子科学研究院学报，2011（5）: 503-505.

A new integrated method of radar signal sorting based on PRI

WEI Ke-you1，2，HUANG Kang2，LIANG Guang2，LIU Hui-jie2
（1.Shanghai Institute of Microsystem and Information Technology，Chinese Academy of Sciences，Shanghai 200050，China；2.Shanghai Engineering Center for Microsatellites，Shanghai 201203，China）

In response to the mixture of constant PRI and fitter PRI，and reducing sorting time，give a new integrated method of signal sorting which combines PRI transform and its improved method. Simulation proves that this method is effective，and can be used to solve the problem of pulse loss.

signal sorting；PRI transform；integrated method；pulse loss

TN971

：A

：1674－6236（2017）01-0190-04

2015-12-22稿件编号：201512227

魏可友（1989—），男，山东临沂人，硕士研究生。研究方向：信号与信息处理、电子侦察技术。