不定方程x(x+1)(x+2)(x+3)=38y(y+1)(y+2)(y+3)的整数解
谌 应 琼
(西南大学数学与统计学院, 重庆 400715)
不定方程x(x+1)(x+2)(x+3)=38y(y+1)(y+2)(y+3)的整数解
谌 应 琼
(西南大学数学与统计学院, 重庆 400715)
运用Pell方程、递归数列、同余式及平方(非)剩余等一些初等方法以及分类讨论的数学思想,证明一种不定方程无正整数解,并得到了其全部整数解。
不定方程;整数解;递归数列;分类讨论;平方剩余
对于形如mx(x+1)(x+2)(x+3)=ny(y+1)(y+2)(y+3),(m,n)=1,m,n∈N+的不定方程,国内外学者一直表现出极大的研究兴趣,尤其是对于形如x(x+1)(x+2)(x+3)=Dy(y+1)(y+2)(y+3)的不定方程[1-8]。1971年,Cohn曾证明,当D=2时不定方程只有正整数解(x,y)=(5,4)[1]。1991年,罗明证明,当D=7时不定方程只有正整数解(x,y)=(4,2)[3]。2007年,程瑶等人证明,当D=11时没有正整数解[4]。2014年,郭凤明等人证明,当D=13时没有正整数解[6]。
在此,主要讨论D=38时不定方程的正整数解以及整数解的情况,运用递归数列、平方(非)剩余等一些初等方法及分类讨论的数学方法,证明式(1)所示不定方程无正整数解,并求此不定方程的全部整数解。
x(x+1)(x+2)(x+3)=38y(y+1)×
(y+2)(y+3)
(1)
首先将式(1)简化成式(2):
(x2+3x+1)2-38(y2+3y+1)2=-37
(2)
通过整理知,方程x2-38y2=-37的全部整数解可以由以下2个(非结合)类给出:
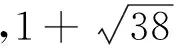
(2x+3)2=4xn+5
(3)
(4)
由此推导出有关变量的关系式:
xn+1=74xn-xn-1,x0=1,x1=265
(5)
(6)
un+1=74un-un-1,u0=1,u1=37
(7)
vn+1=74vn-vn-1,v0=0,v1=6
(8)
u2n= 2un2-1,v2n= 2unvn
(9)
(10)
un+2h≡-un(moduh),vn+2h≡-vn(moduh)
(11)
(12)
下面将运用以上递推式及分类讨论的数学思想,证明式(3)与式(4)当且仅当n=0时成立。由此得到不定方程(x2+3x+1)2-38y2=-37的全部整数解,从而得到式(1)的全部整数解。
1 方程(2x+3)2=4xn+5
在此,讨论当n为何值时4xn+5为完全平方数。
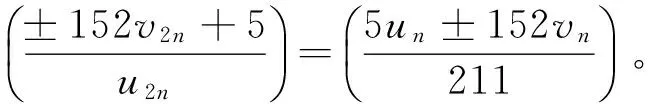
证明 因为2|n,所以由式(7)、式(8)易知,un≡1(mod 2),un≡1(mod 4),u2n≡1(mod 8),un≡1(mod 3),vn≡0(mod 3),5un±152vn≡5(mod 8),5un±152vn≡5(mod 19)。因此由式(9)可知:
引理2 设n≡0(mod 4×33×5×7)且n>0,则式(3)不成立。
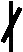
(1)k≡1(mod 4)。
当t≡0,1,2,6,7,8,9,10,13,14,16,17,20,23,27,29,31,32,33,34,36,37,38,39,40,41,43,44,45,48,50(mod 52)时,令m=2t;
当t≡3,4,5,11,18,19,24,25,26,28,35,47,49,51(mod 52)时,令m=32·2t;
当t≡12,21,22,30(mod 52)时,令m=3·7·2t;
当t≡15,42,46(mod 52)时,令m=5·2t。
故,当t(≥1)(mod 52)=0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51时,m
(mod 53)=1,2,3,4,7,9,10,11,17,19,21,22,23,24,28,30,31,33,35,36,38,39,40,41,42,44,45,46,47,50,51,对应{5um+152vm}(mod 211)=42,149,12,106,110,132,207,205,210,130,129,153,10,165,111,168,22,197,146,7,91,32,167,88,15,75,97,140,135,31,2,它们都是模211的平方非剩余。
根据式(10)、式 (12)及引理1,有:
4xn+5≡4x2m+5≡152v2m+5(modu2m)
故
从而得知4xn+5为非平方数,故式(3)不成立。
(2)k≡-1(mod 4)。
当t≡1,3,5,6,7,8,10,11,12,13,14,15,17,18,19,22,24,26,27,28,32,33,34,35,36,39,40,42,43,46,49(mod 52)时,令m=2t;
当t≡0,2,9,21,23,25,29,30,31,37,44,45,50,51(mod 52)时,令m=32·2t;
当t≡4,38,47,48(mod 52)时,令m=3·7·2t;
当t≡16,20,41(mod 52)时,令m=5·2t。
则当t(≥1)(mod 52)=0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51时,m
(mod 53)=2,3,6,7,8,9,11,12,13,14,15,17,18,20,22,23,25,29,30,31,32,34,36,42,43,44,46,49,50,51,52,对应{5um-152vm}(mod 211)=2,31,135,140,97,75,15,88,167,32,91,7,146,197,22,168,111,165,10,153,129,130,210,205,207,132,110,106,12,149,42,它们都是模211的平方非剩余。
根据式(10)、式(12)及引理1,有:4xn+5≡-4x2m+5≡-152v2m+5(modu2m),故:
从而4xn+5为非平方数,故式(3)不成立。
引理3 若式(3)成立,则必须n≡0(mod 4×33×5×7)。
证明 通过对序列{4xn+5}取模来进行证明。此过程分为3步进行,先证明n≡0(mod 15),再证明n≡0(mod 28),最后证明n≡0(mod 54)。
第一步:取mod 31,排除n≡1,2(mod 5),此时4xn+5≡11,11(mod 31),剩n≡0,3,4(mod 5)。
以上mod 31是针对序列{4xn+5}取值,mod 5是因为其剩余序列周期为5,句中“此时”后的算式是排除的理由,因为11为mod 31的平方非剩余。为节省篇幅,后面的证明过程都按这种方式叙述。
取mod 179,排除n≡4(mod 5),此时4xn+5≡136(mod 179),剩n≡0,3(mod 5)。
取mod 1 471,排除n≡3,5,10(mod 15),此时4xn+5≡114,1 327,150(mod 1 471),剩n≡0,8,13(mod 15)。
取mod 4 019,排除n≡8,13(mod 15),此时4xn+5≡551,3 750(mod 4 019),剩n≡0(mod 15)。
第二步:取mod 410 551,排除n≡3,4(mod 7),此时4xn+5≡55 495,332 870(mod 410 551),剩n≡0,1,2,5,6(mod 7)。
取mod 399 601,排除n≡1,5,13(mod 14),此时4xn+5≡1 065,56 545,398 842(mod 39 9601),剩n≡0,2,6,7,8,9,12(mod 14)。
取mod 29,排除n≡8,16,20,23,26(mod 28),此时4xn+5≡19,14,3,14,15(mod 29),剩n≡0,2,6,7,9,12,14,21,22(mod 28)。
取mod 2 969,排除n≡6,22(mod 28),此时4xn+5≡1 204,832(mod 2 969),剩n≡0,2,7,9,12,14,21(mod 28)。
取mod 37,排除n≡1,3(mod 4),此时4xn+5≡29,18(mod 37),剩n≡0,2,12,14(mod 28)。
当n≡2,14(mod 28)时,n≡2,6(mod 8)。取mod 17,排除n≡2,6(mod 8),此时4xn+5≡3,7(mod 17),剩n≡0,12(mod 28)。
当n≡12(mod 28)时,n≡12,26,40(mod 42)。取mod 41,排除n≡12(mod 42),此时4xn+5≡3(mod 41)。取mod 43,排除n≡26(mod 42),此时4xn+5≡32(mod 43)。当n≡40(mod 42)时,n≡4(mod 6)。取mod 73,排除n≡4(mod 6),此时4xn+5≡40(mod 73)。故排除n≡12(mod 28),剩n≡0(mod 28)。
第三步:取mod 127,排除n≡5,8(mod 9),此时4xn+5≡57,3(mod 127),剩n≡0,1,2,3,4,6,7(mod 9)。
取mod 1 063,排除n≡2,6,7(mod 9),此时4xn+5≡842,777,867(mod 1 063),剩n≡0,1,3,4(mod 9)。
取mod 3 673,排除n≡4,19,21,22(mod 27),此时4xn+5≡3 330,387,3 257,1 164(mod 3 673),剩n≡0,1,3,9,10,12,13,18(mod 27)。
取mod 5 669,排除n≡1,9,12,18(mod 27),此时4xn+5≡1 065,5 505,491,170(mod 5 669),剩n≡0,3,10,13(mod 27)。
取mod 107,排除n≡13,37,40(mod 54),此时4xn+5≡63,6,54(mod 107),剩n≡0,3,10,27,30(mod 54)。
取mod 73,排除n≡4(mod 6),此时4xn+5≡40(mod 73),剩n≡0,3,27,30(mod 54)。
当n≡3,27(mod 54)时,n≡1,3(mod 4),取mod 37,排除n≡1,3(mod 4),此时4xn+5≡29,18(mod 37),剩n≡0,30(mod 54)。
当n≡30(mod 54)时,n≡12,30,48,66,84(mod 90)。由于n≡0(mod 15),故可排除n≡12,48,66,84(mod 90)。取mod 89,排除n≡30(mod 90),此时4xn+5≡19(mod 89),剩n≡0(mod 54)。
综上所述,若式(3)成立,则必须使n≡0(mod 15),且n≡0(mod 28),n≡0(mod 54),故有n≡0(mod 3 780)。
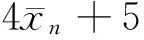
引理4 设n≡0(mod 4×33×5×7)且n>0,则(4)式不成立。
从而证明式(4)不成立。
引理5 若式(4)成立,则必须n≡0(mod 4×33×5×7)。
证明 仿引理3的证明过程,分为3步进行,先证明n≡0(mod 5),再证明n≡0(mod 28),最后证明n≡0(mod 27)。
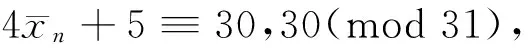
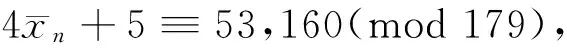

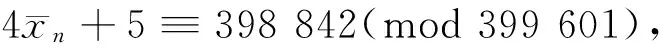
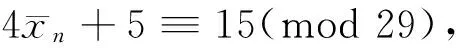
因为n≡0,2(mod 4),排除n≡7,15,21(mod 28),剩n≡0,14(mod 28)。
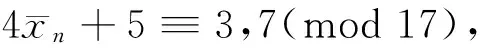
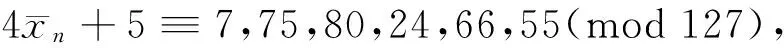
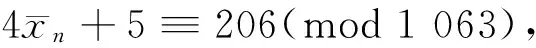
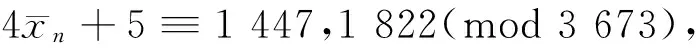
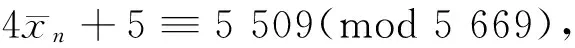
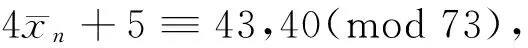
综上所述,若式(4)成立,则必须n≡0(mod 5),且n≡0(mod 28),n≡0(mod 27),故有n≡0(mod 3 780)。
3 讨 论
定理1 不定方程
(x2+3x+1)2-38y2=-37
(13)
的全部整数解是(x,±y)=(0,1),(-3,1),(-1,1),(-2,1)。
证明 由引理2和引理3知,如果式(3)成立,则必须n=0,则有x=0,-3。此时给出方程(13)的前2组解:(x,±y)=(0,1),(-3,1)。由引理4和引理5知,如果式(4)成立,则必须n=0,则有x=-1,-2。此时给出不定方程式(13)的后2组解:(x,±y)=(-1,1),(-2,1)。
定理2 不定方程
x(x+1)(x+2)(x+3)=38y(y+1)×
(y+2)(y+3)
(14)
无正整数解,且其全部整数解是(x,y)=(0,0),(0,-3),(0,-1),(0,-2),(-3,0),(-3,-3),(-3,-1),(-3,-2),(-1,0),(-1,-3),(-1,-1),(-1,-2),(-2,0),(-2,-3),(-2,-1),(-2,-2)。
证明 由式(2)及定理1知,应有y2+3y+1=±1,计算可得y=0,-3,-1,-2,而这些解并非正整数,故式(14)无正整数解。在整数范围内,由定理1可计算出不定方程式(14)的全部整数解。
4 结 语
不定方程的整数解问题一直是数论研究中的一项重要课题。本次证明中,结合了初等数论中的递归数列、平方(非)剩余、同余式等基础知识,并利用了转化为Pell方程的思想以及分类讨论的数学思想,讨论不定方程x(x+1)(x+2)(x+3)=38y(y+1)(y+2)(y+3)整数解的情况。通过研究,得到了其无正整数解的结论,并给出了此不定方程的全部整数解。
[1]COHNJHE.Thediophantineequationx(x+1)(x+2)(x+3)=2y(y+1)(y+2)(y+3)[J].PacificJMath,1971,37:331-335.
[2]PONNUDURAIT.Thediophantineequationx(x+1)(x+2)(x+3)=3y(y+1)(y+2)(y+3)[J].JLondonMathSoc,1975,10:232-240.
[3] 罗明.关于不定方程x(x+1)(x+2)(x+3)=7y(y+1)(y+2)(y+3)[J].重庆师范学院学报(自然科学版),1991,8(1):1-8.
[4] 程瑶,马玉林.不定方程x(x+1)(x+2)(x+3)=11y(y+1)(y+2)(y+3)[J].重庆师范大学学报(自然科学版),2007,7(1):27-30.
[5] 郭凤明,罗明.关于不定方程x(x+1)(x+2)(x+3)=10y(y+1)(y+2)(y+3)[J].西南师范大学学报(自然科学版),2013,38(10):13-16.
[6] 郭凤明,罗明.关于不定方程x(x+1)(x+2)(x+3)=13y(y+1)(y+2)(y+3)[J].重庆师范大学学报(自然科学版),2014,30(5):101-105.
[7] 张洪,罗明.关于不定方程x(x+1)(x+2)(x+3)=Dy(y+1)(y+2)(y+3)(D=21,23)[J].重庆工商大学学报(自然科学版),2015,32(7):56-61.
[8] 王聪.关于不定方程x(x+1)(x+2)(x+3)=30y(y+1)(y+2)(y+3)[J].重庆工商大学学报(自然科学版),2016,33(1):29-32.
[9] 柯召,孙琦.谈谈不定方程[M].哈尔滨:哈尔滨工业大学出版社,2011:15-29.
Research on the Integer Solution of the Diophantine Equation:x(x+1)(x+2)(x+3)=38y(y+1)(y+2)(y+3)
CHENYingqiong
(School of Mathematics and Statistics, Southwest University, Chongqing 400715, China)
With the elementary method of Pell equations, recurrence sequence, congruent form and quadratic residue and mathematical thinking of classification discussion, we have shown that a Diophantine equation has no positive integer solution, and we obtain the total integer solutions of the equation.
Diophantine equation; integer solution; recurrence sequence; classification discussion; quadratic remainder
2016-09-29
国家自然科学基金项目“代数整数的性质研究和无理测度的计算”(11471265)
谌应琼(1993 — ),女,西南大学在读硕士研究生,研究方向为计算数论。
O156
A
1673-1980(2017)02-0120-05

