Coverage Op timization of LTE Networks Based on Antenna Tilt Adjusting Considering Network Load

NhuQuan Phan , ThiOanh Bui , Huilin Jiang ,3, Pei Li , Zhiwen Pan ＊, Nan Liu

1 National Mobile Communications Research Laboratory, South east University, Nanjing 210096, Jiangsu, China

2 Faculty of Mechatronics-Electronics, Lac Hong University, Bien Hoa City 810000, Vi et Nam

3 Institute of electrical engineering, Nanjing Xiaozhuang University, Nanjing 211171, China

* The corresponding author, email: pzw@seu.edu.cn

I. INTRODUCTION

The rapid proliferation of smart devices such as smart phones, laptops, tablets, etc., results in growing service demands of users, e.g.,voice call, games, movie, music and web surfing. The network operators are facing inevitable challenges on how to serve as more users as possible, and to satisfy the user services by increasing the system capacity and ensuring the coverage of the evolved Node B (eNBs).Hence, the capacity and coverage optimization (CCO) problem of Long Term Evolution(LTE) system is an important issue that attracts much interesting [1-6].

Recently, there have been a few researches on CCO [7-21]. In these works, the solutions to optimal coverage problem are presented through schemes such as switching on/off the eNBs, adjusting the transmit power of eNBs,adjusting the antenna tilt angles (ATA), mobility load balancing, cell selection policies and optimizing the placement of antennas. Based on the multiple objects genetic algorithm, in[7], the problem of blind coverage region was handled by jointly adjusting the transmit power and switching on/off the eNBs according to both Received Signal Code Power (RSCP)and Interference Divided by Carrier Ratio(IDCR). A Modified Particle Swarm Optimization (MPSO) algorithm-based heuristic power control scheme is used to reduce the coverage holes, loud neighbor overlap and cell over load of femtocell clusters [8]. The branch and bound search method is employed to get the optimal placement of antennas within the coverage region to maximize coverage [9].

The tilt angle of the eNB antennas plays a crucially important role in determining eNB coverage, minimizing the coverage holes, and managing the interference and handover of users. The eNBs are becoming more and more intelligent that can be automatically adjusted,which makes eNBs more adaptive to dynamic ATA, more flexible in coordinating the eNB coverage, and more feasible in managing the interference of users [10-12]. The tilt angle is considered as a highly efficient parameter for the self-organization network (SON) [13,14]. Base on the aforementioned advantages of ATA, the authors in [15] considered the Call Dropping Ratio (CDR) as the evaluation criterion of the eNBs coverage, and used a sparse sampling algorithm to adjust ATA to decrease the CDR. The CCO was investigated in [16] by using the fuzzy rules to adjust the ATA based on the ATA and spectral efficiency state. To maintain the coverage and reduce the system power consumption, [17] proposed to jointly adjust the mechanical antenna tilt and transmit power after shutting down the adjacent idle eNB. In order to improve the Quality of Service (QoS) in terms of the user throughput, the joint optimization of user association rules and antenna tilt settings are done in [18].To improve coverage and load distribution,[19] jointly considered antenna tilts optimization and cell selection rules by considering the cell individual loads. To increase the cell edge user throughput while simultaneously decreasing the number of uncovered users, a joint downlink and uplink tilt-based SON of CCO under sparse system knowledge scheme was proposed in [20]. The ATA tilting has been studied in our former works [21]. However,ATA is adjusted without the consideration of the network load, thus makes some of the eNBs heavily loaded while others lightly loaded, and the network resource was used inefficiently.

A MPSO-based coverage optimiza tion scheme that adjusts the ATA of eNBs considering the network load to maxim ize the number of users served by eNBs is proposed in this paper.

During the time that the users are crowded in a limited small area, e.g., central plaza, university and stadium, such strong user concentrations will lead to the overload of the local network [22]. Since the Physical Resource Block (PRB) of each eNB is limited, some users will not be allocated to sufficient resource, which results in a low QoS satisfaction for the corresponding users [23, 24]. Without the consideration of the load limitation, load imbalance will happen if we optimize the network coverage by adjusting ATA simply according to the Reference Signal Received Power (RSRP) of users, especially under the aforementioned scenario. This is because in the area with high-density users, too many crowded users eager to connect to the nearest heavy-loaded and resource limited eNBs simultaneously just because theRSRPof the users can be maximized, while the neighboring eNBs are light-loaded with little connected users and abundant residual PRBs. Therefore,in the heavy-load eNB, some users will not be effectively served since lack of resource,while in the neighboring light-load eNB, redundant resource cannot come into effect,which correspondingly results in the broken service of some users and the under-utilization of the PRBs. Therefore, load constraint should be considered in the coverage optimization problem, and how to improve coverage and ensure using the network resource efficiently is a major challenge for system coverage in LTE networks

In this paper, a coverage optimization scheme for LTE networks is proposed by adjusting the ATA of the eNB based on the MPSO algorithm. The network load constraint is taken into consideration. We define the network coverage as the number of users served by the eNBs. It is determined by two metrics of the coverage optimization problem, theRSRPmeasured from the users and the ample degree of the PRBs in the serving eNB. The coverage optimization problem can be solved by adjusting ATA to optimize the number of served users simultaneously guaranteeing the eNBs have enough PRB for all connected users.

First, we present how to determine the number of served users of eNBs. A user is defined as under coverage or being served if theRSRPfrom its serving eNB is larger than theRSRPthreshold and its serving eNB has enough PRBs for all its connected users. Then,the coverage optimization problem is formu-lated as maximizing the number of users under the coverage of eNBs satisfying the above constraints. Since the adjustment of each ATA would affect theRSRPof each user and the load of the eNB, how to cooperatively adjust all ATA to maximize the total number of users under coverage and efficiently use the network resource becomes a critical problem.

The rest of the paper is structured as follows: Section II presents the system model and problem formulation. The MPSO-based ATA adjusting algorithm is demonstrated in Section III. Section IV shows the simulation results. In section V conclusions are drawn.

II. SYSTEM MODEL AND PROBLEM FORMULATION

A 3GPP LTE multi-cell network as shown in Figure 1 withNeNBs,M(M=3N) antennas andKusers is considered, in which the strong and weak signal strengths are shown by solid and dashed lines respectively. We only consider conventional macro base station (eNB),which is divided into three sectors corresponding to three antennas, and assume all users have the same data rate requirement.

2.1 Antenna tilt angle

The ATA denoted as the elevation angle of the antennaψis described in Figure 2. The ATA can be adjusted mechanically or electrically[12]. When we change the ATA, the direction of the antenna’s main lobe will be changed,and the coverage area of eNB will change accordingly.

2.2 Pathloss

To simplify, pathloss is considered as the function depending on the distance [25]

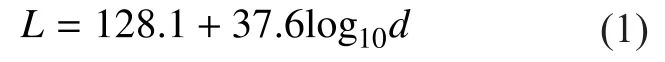
wheredis the distance from user to eNB antenna with the minimum distance from eNB to user is 35 meters.

2.3 Shadow fading model

The shadow fading is usually modeled as logarithmic distributed [26, 27]. Assuming the considered space which has map sizex´yexpressed in square meters. The envelope of the autocorrelation shadow fading function is shown in equation (2)

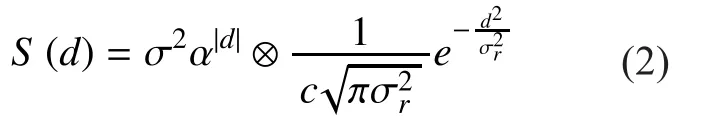
wheredis the spatial variable of the distanceDbetween the eNBs,σis the standard deviation of the log-normal shadow fading (σis usually in the range between 3-10 dB),αis the correlation coefficient between two eNBs spaced by a distance d,is a shape parameterandcis a normalization factor which is determined byS(0)=σ2, the symbol ⊗in equation (2) is the convolution operation.

2.4 The number of users served by eNB with the constraint of network load

RSRPis used as a metric for coverage optimization [3, 18, 20].

At timet, userjwill receive theRSRPfrom antennakof eNBias follow

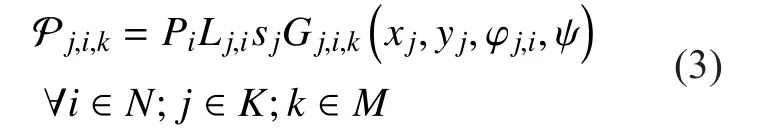
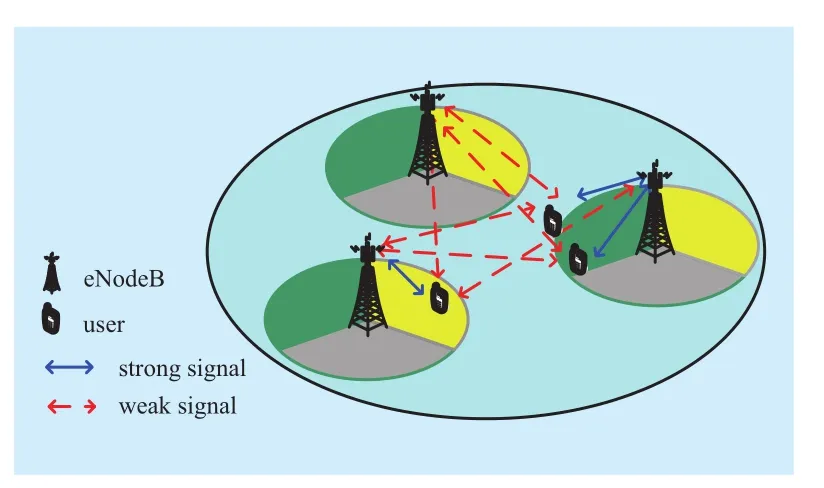
Fig. 1 System model

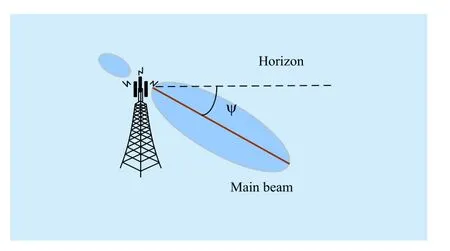
Fig. 2 The relationship between antenna main lobe and tilt angle

wherePiis the transmit power of eNBi;Lj,iis the path loss at userjfrom eNBi; (xj,yj) are the geographical position coordinates of userj;ψis the ATAkof eNBi;sjis position related shadow fading of userj;Gj,i,kis antenna gain at userjfrom antennakof eNBiin dBi and

is the azimuth angle between userjand eNBi,whereare the geographical position coordinates of eNBi.

The users served by eNB antennas are determined as following: if -60o≤φ≤60o,then the antenna 1 of the eNB is serving; if 60o＜φ≤180o, then the antenna 2 of the eNB is serving; if -180o＜φ＜-60o, then the antenna 3 of the eNB is serving.

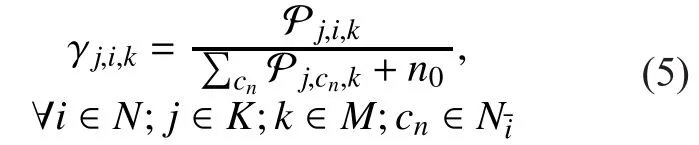
wherecnrepresents all neighboring interfering eNBs of eNBi,n0is the power of additive white Gaussian noise.

Each user selects the eNB with the strongestRSRPas its serving eNB. The connection indicationuj,i,kis

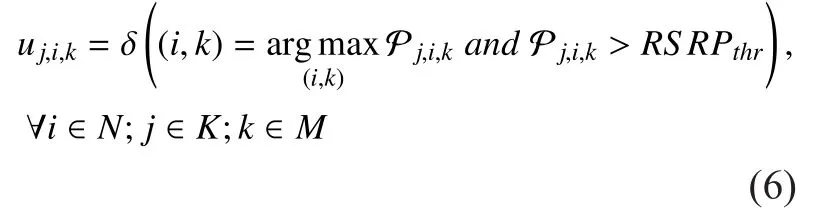
whereRSRPthris the threshold used to evaluate which eNB and which eNB antenna are serving the user, andis a function that equals 1 if the inequality condition can be satisfied.ui,j,kequals 1 if userjconnects to antennakof eNBi, and otherwise equals 0. This equation means userjwill select antennakof eNBias its serving eNB if the maximumRSRPfrom all eNBs is from antennakof eNBi, and the maximumRSRPis larger than theRSRPthreshold.

The bandwidth efficiency of userjfrom antennakof eNBiof the system [23, 28] is

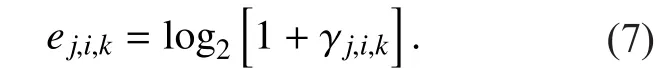
Assuming the whole bandwidthBis allocated to all the users and each user can get equal bandwidth, the userjwill occupy an amount of PRBs of eNBiat antennakas follows

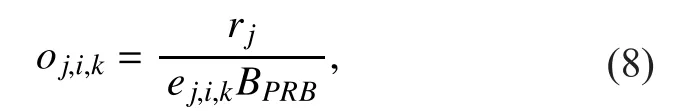
whererjis requirement data rate (bps) of userj;BPRBis the bandwidth of each PRB.

Define the load of userjfrom eNBiat antennakas

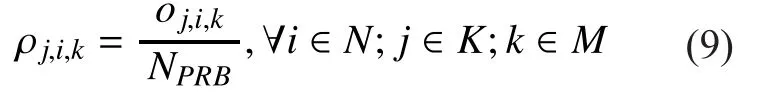
whereNPRBis the total number of PRBs belonged to each eNBi. Then the load of eNBiis

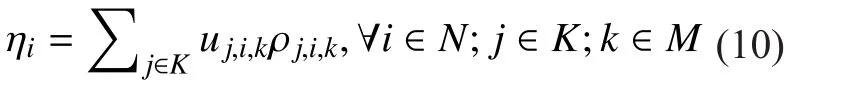
The number of users being served by antennakof the eNBiis then determined with the constraint of the load of serving eNB

The constraint in (11) presents that the serving eNBishould have enough the resource for the connected users. Through formula (11),we can see that the number of users served by eNB is decided by the antenna tilt angle when the number of PRBs belonged to each eNB,the transmit power of eNBs and the horizontal angles are fixed. Therefore, the served user number can be maximized by adjusting the ATA.

Denoteψ={ψ1,ψ2,…,ψM} as the ATA set of the eNBs andψk(∀k∈[1,M]) is the ATA of antennak. Then, the optimization problem can be formulated as

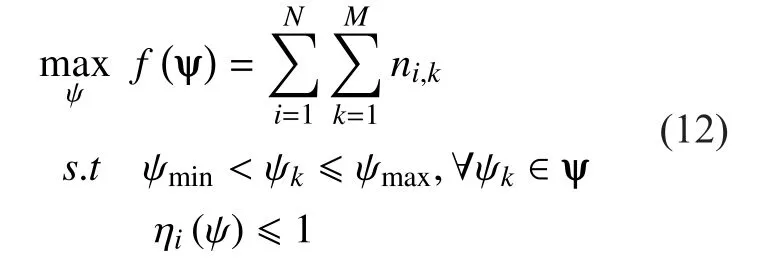
the objective is to maximize the total number of users served by the eNBs through finding the optimal ATA setψwith the constraint of the network load.

The first constraint in (12) tells that the antenna tilt should be adjusted within tilt angle min and max, and the second constraint explains that the given eNB should have enough PRB for the connected users.

III. MPSO-BASED ATA ADJUSTING ALGORITHM

The optimal problem in equations (12) is a non-convex one, which is complex to solve by computational efficient algorithms. It is fortunate that, taking the manifest non-linear and multimodal features of the solution into account, and considering the search space can be constricted very quickly in MPSO algorithm[29, 30], the optimization problem (12) can be solved by means of MPSO. As far as we know,there is not any efficient solution to solve this problem; therefore we propose a MPSO-based ATA adjusting algorithm.

The main target of the proposed MPSO-based ATA adjusting algorithm considering the network load is to solve the aforementioned coverage optimization problem, and the solution is the ATA set. In the MPSO algorithm, a particle swarm known as ATA sets is available. Each particle characterizes a candidate solution to the coverage optimization problem and corresponds to a fitness value determined by the fitness function of the optimization problem. All particles are evolved according to the evolution velocities known as the ATA adjusting scale calculated by their own experience and the global experience of the whole swarm.

ATA are adjusted based on the total number of users served by the eNBs which is known as a fitness function. First, a lot of ATA sets are initialized randomly, each of which corresponds to a fitness value according to the fitness function (12). Second, all sets of ATA are updated in each iteration according to the past experience of the best utility of each ATA set and the global best utility of all ATA sets. The global best ATA can be obtained by iteratively updating these initial ATA sets when achieving better fitness value.

Assume the particle swarm consists ofpparticles, i.e.,psets of ATA. The position of each particle known as ATA set n∈pstands for the potential solution, notated bywhereis the elevation angle of the antennakof setn.ψminandψmaxare the minimum and maximum angle available to the antennas. The MPSO-based ATA adjusting algorithm consists of the following steps:

Step 1.Initialization

Initialize the set ofpATA sets {ψ1(t),ψ2(t),…,ψp(t)}, where each ATA set(∀n∈[1,p]) with each elementψkn∈[ψmin,ψmax] (∀k∈[1,M]) randomly. Initialize the set ofpATA adjustment scale {v1(t),v2(t), …,vp(t)}, whereis the ATA adjustment scale set for ATA setψn, to avoid particle being far away from the searching space, the velocity of the particle generated at its each directionis restricted in [-ψmax,ψmax].

Set the maximum number of the iteration timestmax, the inertia weightω∈[ωmin,ωmax]which can control the impact of the last velocity on the current velocity, in this paper, the inertia weight is set to the following equation

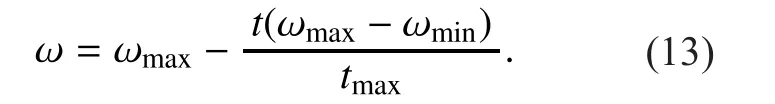
According to the experimental studiesωmin=0.4 andωmax=1. Since the acceleration coefficientsc1andc2, together with the parametersξandχwill determine the sense of the variation of the velocity, according to the empirical studies,c1andc2are taken 1.49, andξandχare randomly number in [0, 1] [31, 32].

Step 2.Operation of the algorithm

In this step, for any ATA setψn(t) belonging to the member of ATA sets, the fitness valuef(ψn) of each setψn(t) is calculated according to the fitness function (12). Base on the constraint of eNB load, the best ATA set experienced by itselfis

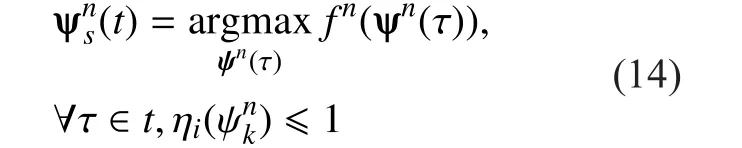
which is the best ATA set corresponding to the maximum number of the served usersni,kobtained so far by the setψn(t) for setnat timet.The global best ATA setψg(t) is

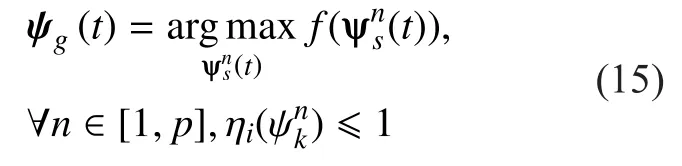
which corresponds to the best ATA obtained so far for all sets of ATA with the constraint of eNB load. Then update the ATA adjustment scale for a typical setvnand the ATA setψn,

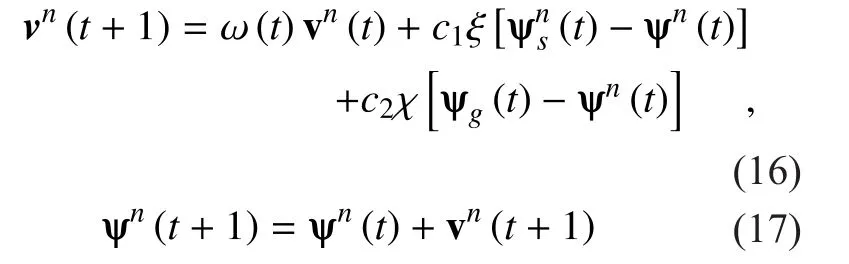
This process is repeated in each iteration cycle. When the maximum number of iterations is satisfied, stop the algorithm and set the ATA of the eNBs with the global bestψg(t).The value of fitness functionf(ψg) can be calculated according to (12). In case the serving eNB does not satisfy the load constraint, i.e.,the remainder PRB of serving eNB is not enough, consider the adjacent eNB offload through repeating the calculation of the best ATA set experienced by itselfψns(t) until the load constraint can be satisfied. The procedureof this step is given in Table I.

Table I The operation of the algorithm

Step 3.Output optimization results

Record the global best ATA set, and set the value of fitness function:

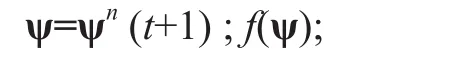
IV. SIMULATION RESULTS

Simulation is conducted and results are presented. The system with 19 eNBs and wraparound model under cell layout in three sectors is considered, the eNBs are in the center of the hexagonal, and the users are generated according to Poisson process, with arrival rate lambdaλ(0.8 user/second, with arrival rate step 0.3 user/second for eNB1, and 0.4 user/second for other ones). All users have the same requirement data rate (100 kbps), and each user randomly moves with a speed in the range of 0-120 km/h in 8 directions (east, west, south,north, north-east, south-east, north-west and south-west). Shadow fading is considered. We assume that the azimuth angle is kept fixed,but the antenna tilt angle can be adjusted, and the height of eNBs and users are the same for all eNBs and users. The system simulation parameters are listed in the below Table II.

In order to make the simulation exactly similar to the realistic networks, we perform the simulation in a dynamic setting. The simulation scenario is in accordance with recommended by 3GPP in [33]. Assuming that all eNBs have the same number of PRBs (50PRBs/ms) and PRB is the smallest unit to allocate to each user [34]. The simulation results are obtained from the 7 eNBs at the center of the 19 wrap-around eNBs.

Figure 3 shows the 7 eNBs at the center of the 19 wrap-around eNBs. The eNBs are shown by green triangles placed at the centre of the hexagons, and the users are shown by red dots.

Figure 4 shows that, the algorithm only need a few iteration times to obtain the global optimal, its convergence is fast. The computational complexity of the solution is polynomial time complexity.

Figure 5 shows the served users number by the 1st, 2nd and 3rd antennas of eNBs before and after adjusting ATA without and with considering the network load, respectively. Obviously, the total number of served users after adjusting ATA without considering the network load is less than the one with considering the network load. And each of eNB is serving a relatively equal amount of users. Hence, we can state that, the proposed algorithm signifi-cantly improve the number of served users,and efficiently solve the load imbalance problem.

The cumulative distribution function (CDF)of theRSRPandSINRof users are shown in Figures 6 and Figure 7, system throughput is illustrated in Figure 8. The proposed algorithm also significantly improved theSINRand the system throughput.

The average load and bandwidth efficiency of the network are shown in Figure 9 and Figure 10. We can see that, the higher the arrival rate of users, the higher the average load, and the higher the arrival rate of users, the a little lower system bandwidth efficiency.

From Figure 4 to 10, obviously, the proposed MPSO based ATA adjusting considering the network load algorithm can significantly increase the number of users served by eNBs,improve the users’SINR, system throughput and also improve the system bandwidth efficiency. It demonstrates that, the proposed algorithm is a promising solution for the optimization of both the eNB coverage area and the system capacity in LTE networks.

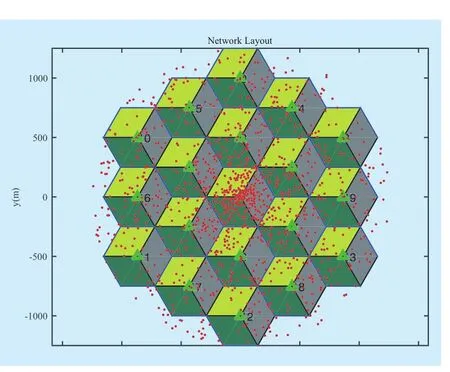
Fig. 3 The simulation system (7 eNBs at the center of 19 wrap-around eNBs)

Table II System Simulation Parameters

V. CONCLUSIONS

In this paper, we defined the network coverage as the number of served users of eNBs considering both theRSRPmeasured from the users and the eNBs’ PRB. The coverage can be optimized by optimizing the number of served users with the constraint of the network load.A MPSO-based coverage optimization scheme that adjusts the ATA of eNBs considering the

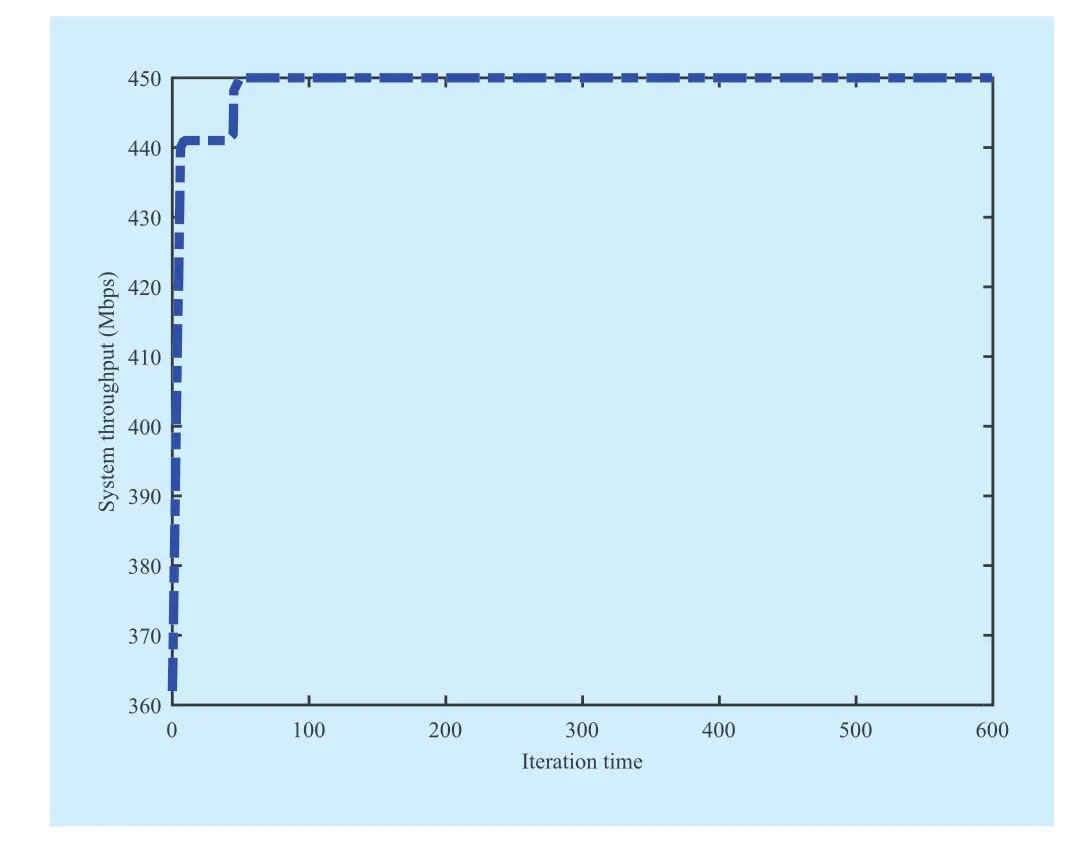
Fig. 4 The convergence of solution

Fig. 5 The served user number before and after adjusting ATA without and with considering the network load

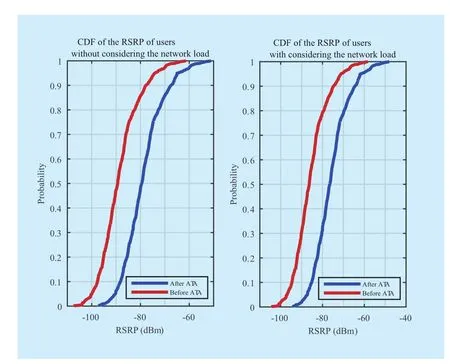
Fig. 6 CDF of users’ RSRP

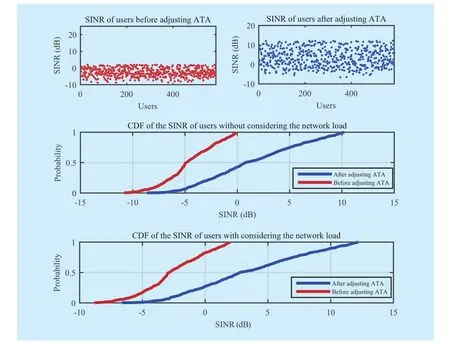
Fig. 7 CDF of users’ SINR

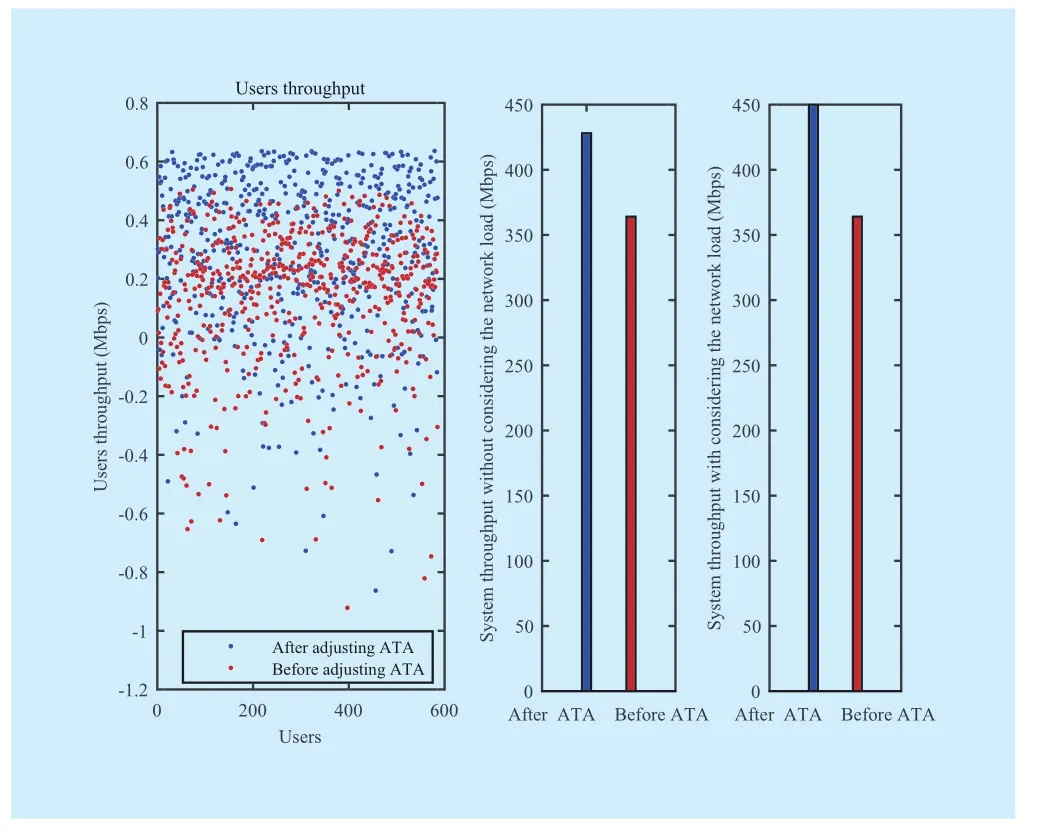
Fig. 8 System throughput

Fig. 9 The average load of the network

ACKNOWLEDGEMENTS

This work is partially supported by National 863 Program (2014AA01A702), National Major Project (2013ZX03001032-004), National Natural Science Foundation (61221002 and 61201170), and the Fundamental Research Funds for the Central Universities (CXLX13 093).

[1] M. Naseer ul Islam, A, Mitschele Thiel, “Reinforcement Learning Strategies for Self-Organized Coverage and Capacity Optimization”,IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, IEEE Press, 2818–2823, 2012.

[2] A. Engels, M. Reyer, X. Xu, et al, “Autonomous Self-Optimization of Coverage and Capacity in LTE Cellular Networks”, IEEE Transactions on Vehicular Technology, vol. 62, no.5, pp 1989–2004,2013.

[3] S. Berger, A. Fehske, P. Zanier, et al, “Online Antenna Tilt-Based Capacity and Coverage Optimization”, IEEE Wireless Communications Letters, vol.3, no.4, pp 437–440, 2014.

[4] R. Rouzbeh, K. Siegfried, C. Holger, “A Fuzzy reinforcement learning approach for self-optimization of coverage in LTE networks”, Bell Labs Technical Journal, vol. 15, no. 3, pp 153–175,2010.

[5] D. Karvounas, P. Vlacheas, A. Georgakopoulos,et al, “An opportunistic approach for coverage and capacity optimization in Self-Organizing Networks”, Future Network and Mobile Summit,Lisboa, Portugal, IEEE Press, 1–10, 2013.

[6] R. Combes, Z. Altman, E. Altman, “Self-organization in wireless networks: a flow-level perspective”, In Proceedings of IEEE INFOCOM,Orlando, America, IEEE Press, 2946–2950, 2012.

[7] M. Gao, L. Huang, H. Cai, “Intelligent Coverage Optimization with Multi Objective Genetic Algorithm in Cellular System”, International Conference on Computer Science & Education(ICCSE), Colombo, Sri Lanka, IEEE Press, 859–863, 2013.

[8] L. Huang, Y. Zhou, J. Hu, et al, “Coverage Optimization for Femtocell Clusters using Modified Particle Swarm Optimization”, IEEE International Conference on Communication (ICC), Ottawa,Canada, IEEE Press, 611–615, 2012.

[9] H. Hafiz, H. Aulakh, K. Raahemifar, “Antenna Placement Optimization For Cellular Networks”,Annual IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), Regina,Canada, IEEE Press, 1–6, 2013.

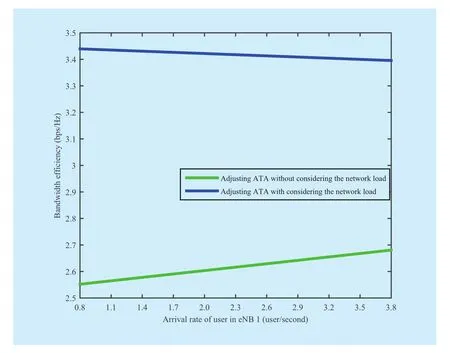
Fig. 10 The bandwidth efficiency of the network

[10] B. Partov, D.J. Leith, R. Razavi, “Utility fair optimization of antenna tilt angles in LTE networks”,IEEE/ACM Transactions on Networking, vol. 23,no. 1, pp 175–185, 2014.

[11] A. Forkel, A. Kemper, R. Pabst et al, “The eff ect of electrical and mechanical antenna downtilting in UMTS networks”, in Proc. 3rd Int. Conf.3G Mobile Commun. Technol, Conf. Publ. No.489.F, London, England, IEEE Press, 86–90, 2002.

[12] F. Athley and M. N. Johansson, “Impact of Electrical and Mechanical Antenna Tilt on LTE Downlink System Performance”, in Proc. 71st IEEE VTC-Spring, Taipei, China, IEEE Press, 1–5,2010.

[13] D. Lee, S. Zhou, X. Zhong, et al, “Spatial modeling of the traffic density in cellular networks”,Wireless Communications, IEEE, vol. 21, no. 1,pp 80–88, 2014.

[14] M. Amirijoo, L. Jorguseski, R. Litjens, at el, “Effectiveness of cell outage compensation in LTE networks”, 2011 IEEE Consumer Communications and Networking Conference (CCNC), Las Vegas, America, IEEE Press, 642–647, 2011.

[15] A. Thampi, D. Kaleshi, P. Randall, et al, “A Sparse Sampling Algorithm for Self-Optimization of Coverage in LTE Networks”, International Symposium on Wireless Communication System(ISWCS), Paris, France, IEEE Press, 909–913,2012.

[16] M. Naseer ul Islam, A. Mitschele Thiel, “Cooperative Fuzzy Q-Learning for Self-Organized Coverage and Capacity Optimization”, IEEE International Symposium on Personal Indoor and Mobile Radio Communications (PIMRC),Sydney, Australia, IEEE Press, 1406–1411, 2012.

[17] Y. Gao, Y. Li, S. Zhou, et al, “System Level Perfor-mance of Energy Efficient Dynamic Mechanical Antenna Tilt Angle Switching in LTE-Advanced System”, IEEE International Wireless Symposium(IWS), Beijing, China, IEEE Press, 1–4, 2013.

[18] A.J. Fehske, H. Klessig, J. Voigt, et al, “Concurrent Load Aware Adjustment of User Association and Antenna Tilts in Self-Organizing Radio Networks”, IEEE Transactions on Vehicular Technology, vol. 62, no. 5, pp 1974–1988, 2013.

[19] H. Klessig, A. Fehske, G. Fettweis, et al, “Improving Coverage and Load Conditions Through Joint Adaptation of Antenna Tilts and Cell Selection Rules in Mobile Networks”, Wireless Communication Systems (ISWCS), 2012 International Symposium on, Paris, France, IEEE Press,21–25, 2012.

[20] S. Berger, M. Simsek, A. Fehske, at el, “Joint Downlink and Uplink Tilt-Based Self-Organization of Coverage and Capacity under Sparse System Knowledge”, IEEE Transactions on Vehicular Technology, vol. 65, no. 4, pp 2259–2273,2016.

[21] P. NhuQuan, J. Huilin, B. ThiOanh, at el, “A Modified Particle Swarm Optimization Based Antenna Tilt Angle Adjusting Scheme for LTE Coverage Optimization”, Journal of Southeast University, vol. 31, no. 4, pp 443–449, 2015.

[22] D. W. Kifle, B. Wegmann, I. Viering, at el, “On the potential of traffic driven tilt optimization in LTE-A networks”, in IEEE International Symposium on Personal Indoor and Mobile Radio Communications (PIMRC), London, England,IEEE Press, 2909–2913, 2013.

[23] L. Zhihang, W. Hao, P. Zhiwen, et al, “Joint Optimization on Load Balancing and Network Load in 3GPP LTE Multi-cell Networks”, 2011 International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China,IEEE Press, 1–5, 2011.

[24] K. Toda, T. Yamamoto, T. Ohseki, et al, “Load Balancing Techniques Based on Antenna Tilt and Handover Timing Control”, 2013 IEEE 78th Vehicular Technology Conference (VTC Fall), Las Vegas, America, IEEE Press, 1–6, 2013.

[25] 3GPP TR 36.814 V9.0.0, “Further advancements for E-UTRA physical layer aspects”, releases 9,2010.

[26] M. Gudmundson, “Correlation Model For Shadow Fading In Mobile Radio System”, Electronics Letters, vol. 27, no. 23, pp 2145–2146, 1991.

[27] D. Giancristoraro, “Correlation model for shadow fading in mobile radio channels”, Electronics Letters, vol. 32, no. 11, pp 958–959, 1996.

[28] A. Lobinger, S. Stefanski, T. Jansen, et al. “Load Balancing in Downlink LTE Self-Optimizing Networks”, Vehicular Technology Conference (VTC 2010-Spring), 2010 IEEE 71st, Taipei, China, IEEE Press, 1–5, 2010.

[29] Y. Shi, R. Eberthart, “A modified particle swarm optimizer”, IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence(WCCI), Anchorage, America, IEEE Press, 69–73,1998.

[30] B. Qinghai, “Analysis of Particle Swarm Optimization Algorithm”, Computer and Information Science, vol. 3, no. 1, pp 180–184, 2010.

[31] Y. Tong Liu, M. Yin Fu, H. Bin Gao, “Multi-Threshold Infrared Image Segmentation Based on the Modified Particle Swarm Optimization Algorithm”, 2007 International Conference on Machine Learning and Cybernetics, Hong Kong,China, IEEE Press, 383–388, 2007.

[32] S. Lalwani, R. Kumar, N. Gupta, “A study on inertia weight schemes with modified particle swarm optimization algorithm for multiple sequence alignment”, 2013 Sixth International Conference on Contemporary Computing (IC3),Noida, India, IEEE Press, 283–288, 2013.

[33] 3GPP TR 25.814 V7.1.0, “Further advancements for E-UTRA physical layer aspects”, 2010.

[34] 3GPP TS 36.201 V9.1.0, “LTE physical layer: General description”, 2010.