应用距离搜索的低轨空间碎片初始轨道确定方法

章品 桑吉章 潘腾 李怀锋

(1 武汉大学测绘学院，武汉 430079) (2 北京空间飞行器总体设计部，北京 100094)



应用距离搜索的低轨空间碎片初始轨道确定方法

章品1桑吉章1潘腾2李怀锋2

(1 武汉大学测绘学院，武汉 430079) (2 北京空间飞行器总体设计部，北京 100094)

使用低轨天基光学望远镜扫描式观测低轨空间碎片，由于两者的相对运动较快，只能获得很短时间内的角度观测值(甚短观测弧段)，使用传统的Gauss方法和Gooding方法很难得到精确的空间碎片初始轨道。为此，文章提出了一种新的方法，在给定的一组角度观测值中，通过搜索其中2个时刻的距离信息，将纯角度的初始轨道确定问题转换为基于2个位置矢量的初始轨道确定问题；再利用其他时刻的角度观测值进行检核和约束，筛选出最优的初始轨道结果。利用文章方法对空间碎片在10～60 s内的503个观测弧段进行处理，结果表明，其定轨误差与角度观测值变化率有关。将文章方法所得结果与Gauss方法和Gooding方法进行比较，证明文章方法在解的成功率和精度上都显著优于其他2种方法，能很好地确定空间碎片的初始轨道。

空间碎片；天基光学观测；初始轨道确定；距离搜索；角度观测值

1 引言

自人类进入太空以来，人类的太空活动越来越频繁，导致空间碎片越来越多。目前，直径在1 cm以上的空间碎片多达50万个，其中约90%的碎片都集中分布在轨道高度2000 km以下的低轨区域内。大量高速飞行的空间碎片严重威胁了航天器的安全运行，一旦发生碰撞，后果不堪设想。因此，对空间碎片进行有效的监控、编目和管理，并定期开展在轨碰撞预警，变得至关重要。截至2017年3月，北美航天防御司令部(NORAD)数据编目的在轨空间目标多达18 000个，还有大量未知的空间目标有待去确定它们的轨道信息。对于大量没有任何先验信息的空间碎片，要想实现精密定轨和编目，首先就要确定其初始轨道。

目前，我国主要利用地基光学跟踪网监测空间碎片。对于低轨空间碎片，地基光学观测每天的观测时间只有晨昏各约2 h，所能观测的空间碎片数量有限；此外，受跟踪网区域的限制，观测不能实现全球覆盖。这是我国高精度碎片数据库和空间碰撞预警系统建立所面临的主要困难之一。而使用低轨天基光学望远镜对低轨空间碎片进行扫描式探测时[1]，天基平台自身的运动特性导致观测弧段很短[2]，只能获得较短时间内的角度观测值(赤经、赤纬)。现有的Gauss方法[3-4]和Gooding方法[5-7]主要应用于地基长弧段目标的初始轨道确定，在处理较短时间内的角度观测值时，会出现迭代不收敛或者平凡解(收敛于天基平台自身轨道)等现象，很难得到好的定轨结果[8-9]。

随着计算机的发展，计算能力得到不断提升，为有效利用低轨天基光学望远镜的角度观测值进行空间碎片初始轨道确定提供了条件。为此，本文提出了一种应用距离搜索的低轨空间碎片初始轨道确定方法，可处理很短时间内的角度观测值，筛选出最优的初始轨道结果。

2 应用距离搜索的初始轨道确定方法

由于观测误差，对于很短时间内的角度观测值，Gauss方法在解算距离方程时，容易出现解算失败或者所解算的距离误差很大的情况，导致Gauss方法基本失效。而Gooding方法需要较精确的距离初值，收敛条件比较苛刻，因此，尽管解的收敛性比Gauss方法好，但在很多情况下仍不能获得可靠的初始轨道解。为解决较短时间内天基望远镜到空间碎片的距离难于解算的困难，本文提出一种应用距离搜索的低轨空间碎片初始轨道确定方法。在一个观测弧段中，取2个观测时刻(一般为首尾时刻)，在一定范围内以一定步长分别假设这2个时刻的距离值，根据每组距离值的组合，可以得到这2个时刻空间碎片相对地心的位置矢量，继而可以确定一组轨道参数。根据这组轨道参数，可以计算出其他时刻的角度观测值，并与实际角度观测值进行比较，以得到的残差作为检核标准，从而筛选出合适的初始轨道确定结果。这一方法受观测弧段长度影响较小，只要多次求解Lambert问题[4]即可，且解的质量可用其他角度观测值来控制。

2.1 距离搜索

图1为天基观测示意，O―XYZ坐标系为天球惯性坐标系，坐标原点为地球质心，X轴指向春分点方向。假设在t1,t2,…,tn时刻分别获得角度观测值赤经为(δ1,δ2,…,δn)和赤纬(φ1,φ2,…,φn)。在天球惯性坐标系下，通过式(1)～(3)，可得天基望远镜到空间碎片方向(即望远镜视线方向)的单位矢量Li(i=1,2,…,n)坐标(Lxi，Lyi，Lzi)。

(1)

(2)

(3)

图1 天基观测示意Fig.1 Diagram of space-based observation

选取t1到tk弧段为定轨弧段，tk+1到tn弧段为控制弧段。用ρ1，ρk表示t1，tk时刻的观测距离，如果知道ρ1，ρk，就可根据空间碎片的位置矢量ri=ρiLi-Ri(i=1,k)得到2个位置矢量r1，rk，其中，Ri为天基望远镜到地球质心的矢量。这样，纯角度的初始轨道确定问题就转换为基于2个位置矢量的轨道确定问题(即初始轨道确定的Lambert问题)。不妨在一定区间内以一定步长分别假设ρ1，ρk的值，每个组合可以相应计算出一组轨道参数，再通过控制弧段的角度观测值来检核该组轨道参数的准确性。

2.2 筛选标准

(4)

(5)

这样就可以得到(n-k)组赤经、赤纬的偏差值，并计算这些偏差值序列的平均值、均方根等统计参数。以赤经的偏差值Δδ为例，为简化后续的表达，令m=n-k，yi=Δδi，则序列y的平均值为

(6)

均方根为

(7)

用简单的线性回归模型对序列y建立模型如下。

(8)

式中：因变量x表示当前历元与参考历元之间的差值；β0为回归直线在y轴上的截距，β1为直线的斜率，可用最小二乘估计这2个系数，见式(9)。

(9)

该回归方程的误差和它的中误差为

(10)

(11)

由于真实角度观测值中可能存在粗差，导致y值与建立的回归直线有较大的偏离。为了更好地用一条直线对y进行拟合，利用中误差σ对粗差进行简单的剔除。如果υi>3σ(i=1,2,…,m)，那么yi被剔除，剩下的y组成新的序列，并按照式(9)～(11)的过程得到新的β1以及y轴截距β0。

同理，Δφi(i=1,2,…,m)序列也可以得到相应的参数。在这些参数中，选取均方根和斜率来检核计算出来的轨道的可靠性。如前所述，如果Δδi，Δφi是在0值附近小幅度波动的噪声序列，也就是说，其均方根以及序列整体的斜率都接近于0的话，可以认为本次的定轨结果是比较准确可靠的。这样，可以对均方根和斜率分别给定一个阈值，从而筛选出符合要求的初始轨道确定结果(即轨道六根数中的半长轴a、偏心率e、倾角i、升交点赤经Ω、近地点幅角ω和平近点角M)，构建轨道集合，并分别求解轨道六根数的平均值，得到一个最优解。

本文方法的流程如图2所示，DRMS和Dβ分别为设定的均方根和斜率的阈值。

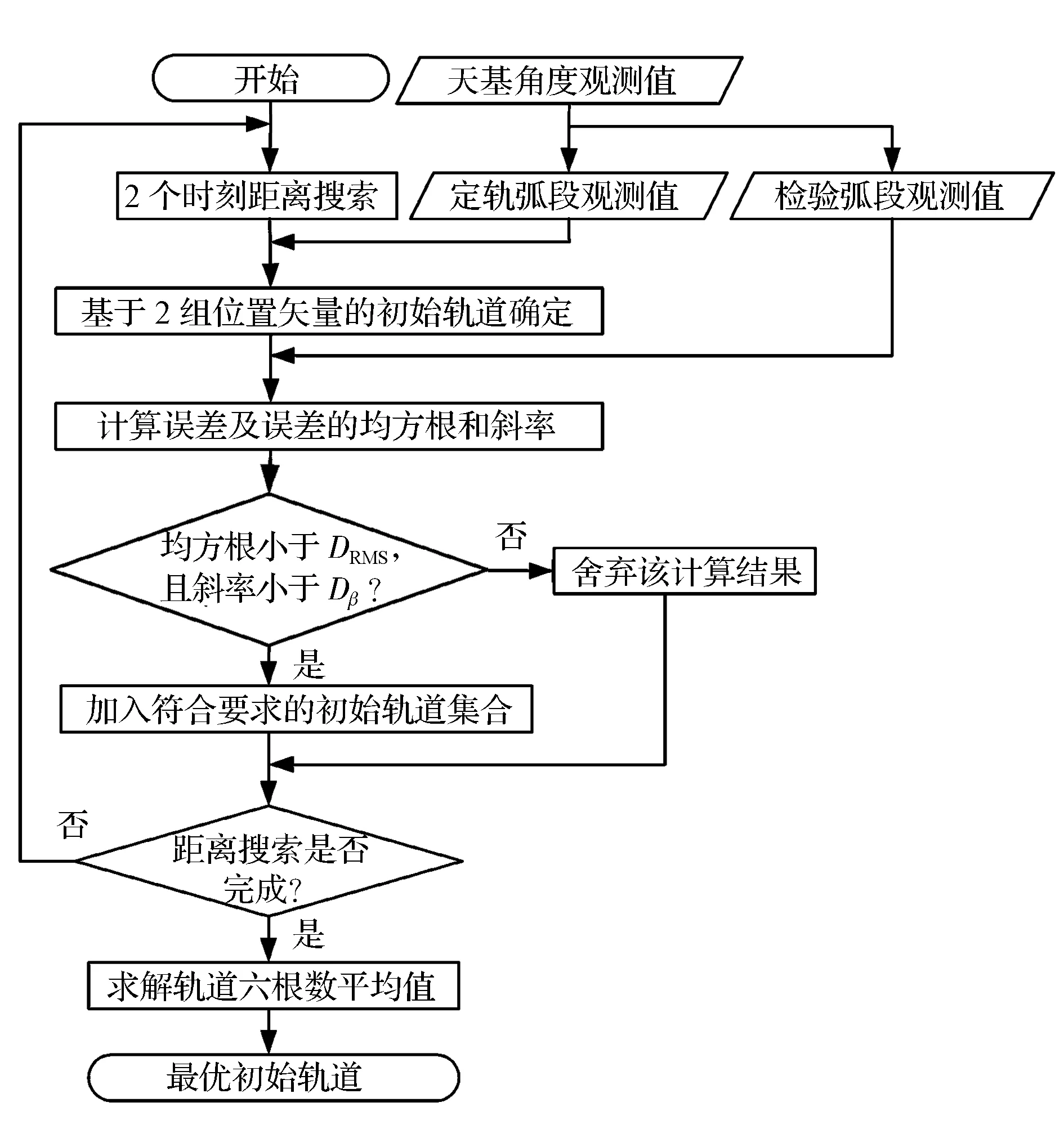
图2 初始轨道确定方法流程Fig.2 Flowchart of method for initial orbit determination

3 仿真试验及结果分析

3.1 仿真设定

以NORAD编目库中的空间碎片二行参数(TLE)为基础来产生仿真角度观测值。TLE是NORAD基于低阶解析摄动理论产生的用于计算地球轨道飞行器位置和速度的一组平均轨道根数，具有更新速度快、覆盖空间物体数量多、获取方便等特点[10]。天基平台的轨道根数如表1所示(参考历元为2014年11月15日0时)，天基光学望远镜与天基平台固连，望远镜光轴指向为轨道的法线方向，即始终垂直于轨道面，望远镜视场为6°×6°，角度观测误差为2″。

通过模拟观测试验，在2014年11月15日和16日的观测日期内，得到了落入望远镜视场里的1330个近圆低轨空间碎片，以及这些空间碎片落入视场内的时间(即观测时长)。针对这些空间碎片，考虑完整的摄动力影响，通过精密数值积分获得其“真轨道”，从而进一步获得观测弧段内各观测时刻(观测时间间隔为0.1 s)的模拟角度观测值(赤经、赤纬)。因为观测时长短于10 s，解的成功率降低，长于60 s的情况又较少，所以选取时长在10～60 s范围内的空间碎片(观测时长超过60 s的空间碎片，只取前60 s的角度观测值)，共503个，进行初始轨道解算。分别使用Gauss方法、Gooding方法和本文方法，根据这503个空间碎片的角度观测值进行初始轨道确定，如果解存在，则得到该空间碎片的轨道六根数，并与空间碎片轨道参数参考值求差，得到初始轨道参数的误差。另外，由于考虑的是近圆轨道空间碎片，即偏心率接近于0，轨道近地点所在位置比较模糊，且半长轴、倾角和升交点赤经能有效反映轨道的形状，因此在评定3种方法初始轨道确定精度时只比较分析这3个参数的误差。

表1 天基平台轨道根数

3.2 本文方法仿真分析

3.2.1 仿真结果

使用本文方法处理503个甚短观测弧段，初始轨道解算获得488个解，解算成功率达到97%。定轨精度方面，本文方法确定的半长轴、倾角和升交点赤经误差如图3所示。

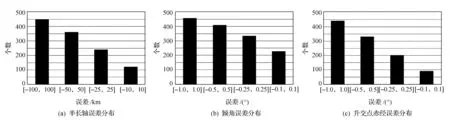
图3 半长轴、倾角和升交点赤经误差分布Fig.3 Error distribution of semi-major axes， inclination and RAAN

由图3可知，本文方法确定的488个解中，半长轴误差绝对值不超过100 km的有450个，占总数的92.2%，表明半长轴误差主要集中在100 km范围内；另外，有121个解落在了[―10，+10] km区间内，占总数的24.8%。类似地，倾角误差绝对值和升交点赤经误差绝对值小于1°的分别有458个和442个，分别各占总数的93.9%和90.6%。倾角误差绝对值小于0.1°的观测弧段数目达到了227个，占46.5%，接近总数的50%；升交点赤经误差绝对值小于0.1°的也有92个，占总数的18.9%。

3.2.2 误差分析

本质上，初始轨道解算的参数精度取决于是否能从角度观测值中提取有效的距离信息。当天基光学望远镜与空间碎片接近于平行运行时，也即两者轨道面夹角较小时，角度观测值的几何条件较差，难以提取有效的距离信息，这会影响最终的初始轨道确定精度。定轨误差与轨道面夹角之间的关系如图4所示。可见，天基光学望远镜和空间碎片轨道面之间的夹角对初始轨道确定结果，特别是对轨道倾角和升交点赤经的解有较大的影响。轨道面夹角大，也就意味着空间碎片与天基光学望远镜有较大的相对位置变化，角度观测值的时间变率比较大。因此，角度观测值随时间的变化率有可能为判断初始轨道解算结果的好坏提供一些依据。

表2给出了半长轴、倾角和升交点赤经误差根据赤经、赤纬变化率的统计结果，其中区间A=(-0.05，+0.05)(°)/s。当赤经与赤纬的变化率都小于0.05(°)/s时(总共84个观测弧段)，半长轴误差大于100 km的比例为26.19%，倾角和升交点赤经误差大于1°的比例分别为16.67%和26.19%。另一方面，当赤经与赤纬的变化率至少有一个大于0.05(°)/s时(总共404个观测弧段)，半长轴误差大于100 km的比例降到3.96%，倾角和升交点赤经误差大于1°的比例分别降到3.96%和5.94%。也就是说，当角度观测值的变化率很小时，定轨解算误差较大的可能性明显上升。如果把赤经和赤纬变化率都小于0.05(°)/s的情况剔除，则半长轴误差超过100 km的比例从7.79%降至3.96%，同时倾角和升交点赤经误差大于1°的比例分别从6.15%和9.43%降到3.96%和5.94%。

将赤经和赤纬变化率都小于0.05(°)/s的观测弧段过滤掉，统计了剩余的404个观测弧段的初轨确定结果，并与过滤前的结果进行比较，如图5所示。可以发现，经过过滤后，各区间的百分比都有了一定的提高，或至少维持原有水平。

图4 半长轴、倾角、升交点赤经误差与轨道面夹角的关系Fig.4 Errors of semi-major axis， inclination and RAAN vs. intersection angles of two orbits

条件观测弧段个数|Δa|>100km|Δi|>1°|ΔΩ|>1°个数所占百分比/%个数所占百分比/%个数所占百分比/%δ·∈A&&φ·∈A842226.191416.672226.19δ·∉A||φ·∉A404163.96163.96245.94合计488387.79306.15469.43

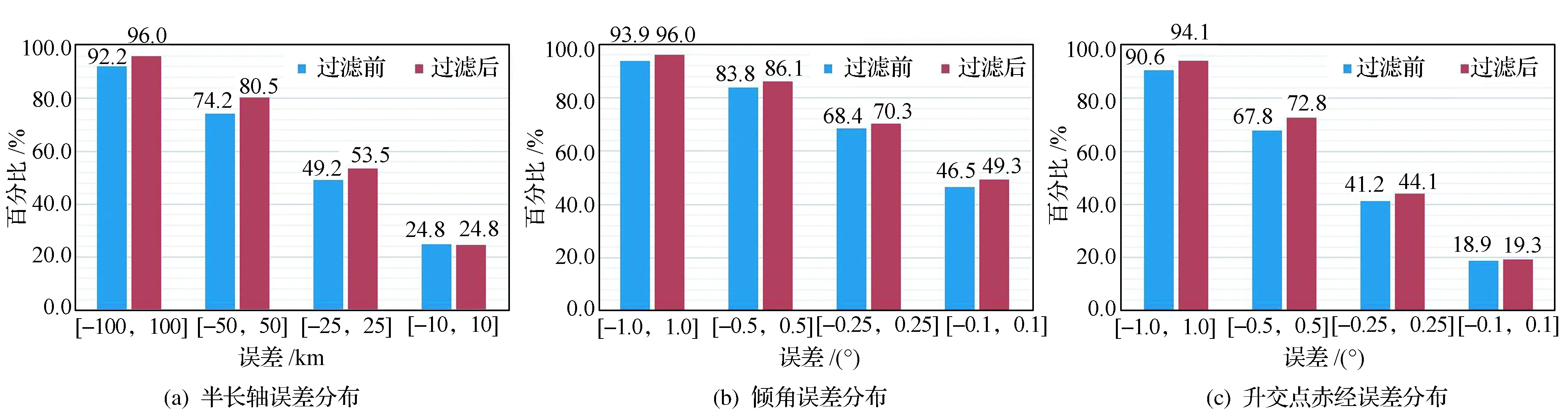
注：“过滤前”表示所有解算结果，“过滤后”表示去除赤经和赤纬变化率都小于0.05(°)/s的观测弧段后的解算结果。图5 过滤前后半长轴、倾角和升交点赤经误差分布Fig.5 Error distribution of semi-major axis， inclination and RAAN before and after filtration

3.3 与Gauss方法和Gooding方法的比较

采用Gauss方法和Gooding方法对相同的角度观测值进行处理。从初始轨道确定的解的个数和解的精度两个方面，综合比较Gauss方法、Gooding方法和本文方法的初始轨道确定效果。3种方法解算观测时长在10～60 s范围内的503个观测弧段，解的结果如表3所示。可见，在解的存在性方面，Gooding方法要优于Gauss方法，而本文方法相对于Gooding方法又有显著的提升。

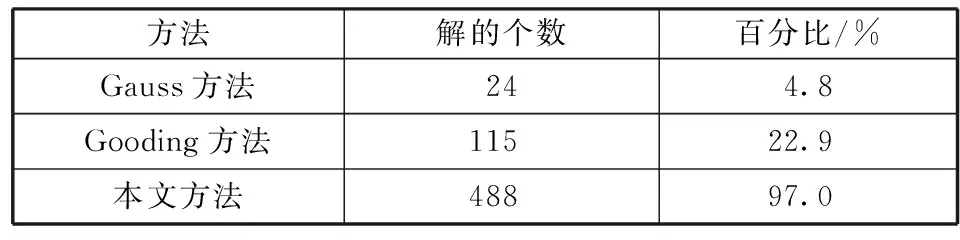
表3 3种方法的解

图6分别为3种方法得到的半长轴、倾角和升交点赤经误差的分布。可以看出，在各误差区间内，本文方法的百分比始终最大，Gooding方法次之，Gauss方法最小。以半长轴误差分布为例，在误差范围为[―500,+500]km时，也就是说初始轨道确定的半长轴精度能达到500 km时，Gauss方法的解只有16.7%，Gooding方法的有99.1%，本文方法有99.8%；虽然在该区间内Gooding方法和本文方法相差不大，但当精度提高到100 km时，Gooding方法的比例迅速减小到57.4%，而本文方法仍有92.2%的解达到该精度，此时，Gauss方法只有8.3%；当区间缩小到[―10，+10]km时，Gauss方法并不存在半长轴误差的绝对值小于10 km的解，Gooding方法也只有9.6%，而本文方法有24.8%的解能满足该精度要求。

倾角和升交点赤经误差也有类似的规律，因而可以得出结论：在处理很短时间内的角度观测值时，本文方法解的成功率和精度比Gauss方法和Gooding方法有明显的优势。

另外，对3种方法的解算结果分别进行统计，它们的半长轴、倾角和升交点赤经的误差绝对值|Δa|，|Δi|，|ΔΩ|的统计结果如表4所示。可以发现，对于|Δa|，|Δi|，|ΔΩ|，本文方法的平均值和均方根都是最小的，Gooding方法次之，Gauss方法最大。经过过滤后，本文方法获得的各轨道参数误差的平均值、均方根和最大值都得到了改善，特别是最大值方面，过滤前，本文方法获得的|Δa|和|Δi|的最大值都要大于Gooding方法，而过滤后的最大值明显减小，且小于Gooding方法。这也表明，在牺牲一定解算成功率的前提下，通过过滤处理可以有效过滤掉偏差过大的粗差，从整体上改善解算精度。

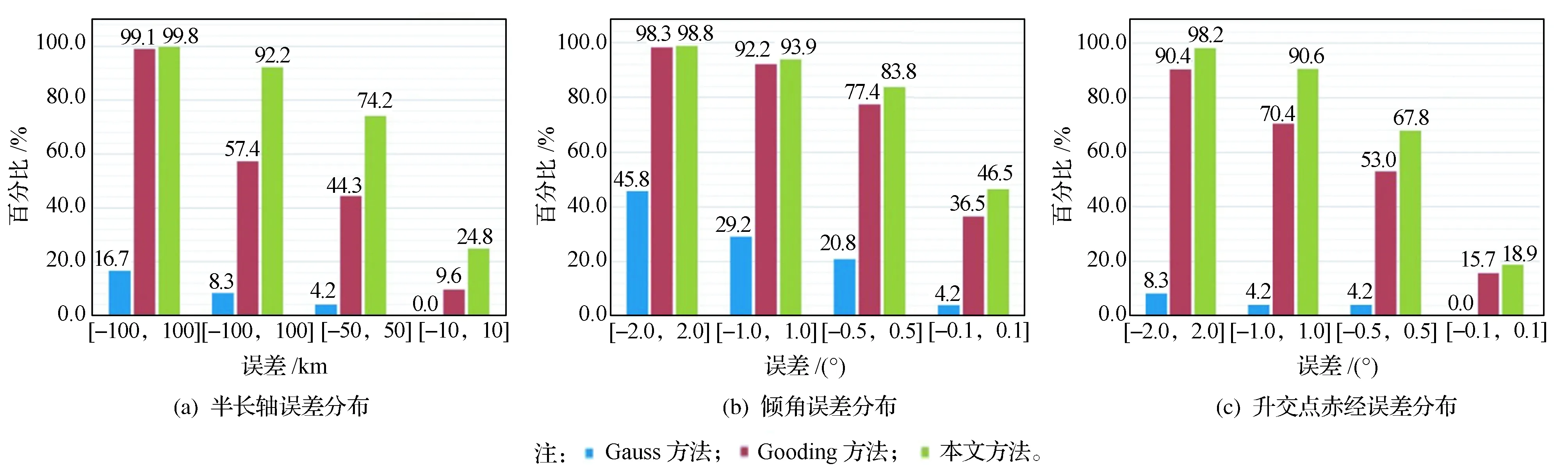
图6 3种方法得到的半长轴、倾角和升交点赤经误差分布Fig.6 Errors distribution of semi-major axis， inclination and RAAN using three methods

方法|Δa|/km|Δi|/(°)|ΔΩ|/(°)平均值均方根最大值平均值均方根最大值平均值均方根最大值Gauss方法19997.755208.8255370.68.0513.5845.4816.8224.0375.09Gooding方法122.8176.1595.10.350.582.690.811.153.62本文方法过滤前40.968.1629.10.280.544.500.460.663.34过滤后32.448.8318.30.230.371.750.390.542.94

4 结束语

本文提出了一种应用距离搜索确定低轨空间碎片初始轨道的方法，并进行了仿真试验。试验结果表明，本文方法能根据很短时间内的角度观测值确定低轨空间碎片的初始轨道，比传统的Gauss方法和Gooding方法能够有效提高解算成功率以及精度。此外，初始轨道确定的误差与天基平台和空间碎片之间的轨道面夹角大小有比较明显的关系，当夹角很小，也即角度观测值的变化率都接近于0时，解算出的初始轨道参数有较大误差的概率明显上升。因此，在进行初始轨道确定之前，可以先对角度观测值做预处理，过滤掉角度观测值变化率很小的观测弧段(阈值可设置为0.05(°)/s)，这样处理虽然会在一定程度上减少解的数量，但能有效地避免出现解算误差过大的情况，改善整体的解算精度。本文方法获得的更高精度的空间碎片初始轨道，可为空间碎片更精确的定轨和预报，以及我国对空间碎片的监测和碰撞预警提供一种有效途径。

References)

[1] Fujimoto K,Scheeres D J. Correlation and initial orbit determination for short-arc optical observations [R/OL].[2017-02-23].https://www.researchgate.net/publication/253881513_Correlation_and_Initial_Orbit_Determination_for_Short-Arc_Optical_Observations

[2]Ansalone L,Curti F. A genetic algorithm for initial orbit determination from a too short arc optical observation [J]. Advances in Space Research,2013,52(3): 477-489

[3]Vallado D A,McClain W D. Fundamentals of astrodynamics and applications [M]. Berlin：Springer Science & Business Media,2001

[4]Escobal P R. Methods of orbit determination [J]. New York: Wiley,1965

[5]Gooding R H. A new procedure for orbit determination based on three lines of sight (angles only) [R/OL]. [2017-02-23]. https://www.researchgate.net/publication/235117379_A_New_Procedure_for_Orbit_Determination_Based_on_Three_Lines_of_Sight_Angles_Only

[6]Gooding R H. A new procedure for the solution of the classical problem of minimal orbit determination from three lines of sight [J]. Celestial Mechanics and Dynamical Astronomy,1996,66(4): 387-423

[7]Vallado D A. Evaluating Gooding angles-only orbit determination of space based space surveillance measurements [J/OL].[2017-02-23]. https://www.researchgate.net/publication/228994563_Evaluating_Gooding_Angles-only_Orbit_Determination_of_Space_Based_Space_Surveillance_Measurements

[8]王秀红，李俊峰，王彦荣.天基照相机监测空间目标定轨方法及精度分析[J].光学精密工程，2013，21(6)：1394-1403

Wang Xiuhong,Li Junfeng， Wang Yanrong. Orbit determination and precision analysis of space object with space-based camera [J]. Optics and Precision Engineering,2013,21(6): 1394-1403 (in Chinese)

[9]刘磊.基于天基监视的空间目标测向初轨确定研究[D].长沙：国防科学技术大学，2010

Liu Lei. Study on the initial orbit determination of space targets with space-based surveillance [D]. Changsha： National University of Defense Technology,2010 (in Chinese)

[10]Levit C,Marshall W. Improved orbit predictions using two-line elements [J]. Advances in Space Research,2011,47(7): 1107-1115

(编辑：夏光)

Initial Orbit Determination Method Based on Range Searching for LEO Space Debris

ZHANG Pin1SANG Jizhang1PAN Teng2LI Huaifeng2

(1 School of Geodesy and Geomatics,Wuhan University,Wuhan 430079,China) (2 Beijing Institute of Spacecraft System Engineering,Beijing 100094,China)

When a LEO space debris is optically observed in the scanning mode from a LEO space-based telescope,only angular observations in a very short time (very short observation arc)can be collected due to high relative velocity between the debris and the telescope. It is usually difficult to obtain accurate IOD (initial orbit determination) results from such short-arc angles by using traditional Gauss and Gooding methods. In this paper,a new method is proposed to tackle this very short-arc angles-only IOD problem. In a set of given angular observations,the ranges at two epochs are tested through a step-by-step search procedure and making the problem of angles-only IOD transforming to the problem of two position vector IOD. Then,the angular observations of other epochs are used in judgment foundation of the IOD solutions to obtain an optimal solution. The method is applied to process 503 observation arcs of space debris between 10 and 60 seconds,and the results show that the errors of IOD are principally influenced by the variation rate of angular observations. Comparisons with the results using the Gauss and Gooding methods show that,the proposed method is significantly superior over the other two methods in both the solution success rates and accuracy,which can be used to determinate the initial orbit of space debris.

space debris； space-based optical tracking； IOD(initial orbit determination)； range searching； angular observation

2017-03-06；

2017-03-28

国家自然科学基金(41474021)

章品，男，硕士研究生，从事空间碎片轨道确定与预报工作。Email:pzhang1992@whu.edu.cn。

P228.1

A

10.3969/j.issn.1673-8748.2017.02.004