基于Petri网的Walker导航星座备份策略研究

胡敏 宋旭民 杨雪榕

(中国人民解放军装备学院，北京 101416)



基于Petri网的Walker导航星座备份策略研究

胡敏 宋旭民 杨雪榕

(中国人民解放军装备学院，北京 101416)

提出了一种基于Petri网的Walker导航星座备份策略，考虑了导航星座运行中的主要不确定性因素，得到的备份策略能够使星座实际运行可用性与星座期望可用性非常逼近。对Walker 24/3/1:21528 km，55°星座无备份星、仅考虑地面备份，以及考虑在轨和地面均备份三种情况的星座可用性进行了分析，结果表明：采用在轨备份3颗卫星、地面备份3颗卫星的策略能够保证导航星座的平稳运行,可为Walker导航星座备份策略的选取提供借鉴。

Walker导航星座；Petri网；在轨备份；地面备份；星座可用性

1 引言

导航星座备份策略直接影响全球卫星导航系统完好性、可用性和连续性等重要指标的实现，是全球卫星导航系统星座设计的重要内容，也是在卫星发射、运行出现故障时，确保导航系统成功组网和稳定运行的关键。根据全球定位系统(GPS)、全球导航卫星系统(GLONASS)和伽利略(Galileo)三大全球卫星导航系统建设运行的经验，对星座进行必要的备份是确保导航系统连续稳定运行的必要条件。GPS的设计星座包括24颗卫星，但自1993年满星座运行以来，实际卫星数量一直维持在27颗以上，当工作卫星出现故障时，通过在轨备份卫星正常播发导航电文，从而有效地保证了服务性能[1-3]。GLONASS系统在满足标称星座的基础上，在每个轨道面上备份一颗卫星，正常情况下，备份卫星不播发导航信号，处于冷备份状态，只有当工作卫星出现故障时，才启动备份卫星。根据Galileo星座设计方案，为了满足系统完好性、可用性和连续性的要求，Galileo系统在每个轨道面上均部署一颗备份卫星，正常情况下，备份卫星不发射信号，而当某个工作卫星出现故障时，该备份卫星将在地面控制下漂移到相应位置完成补充，确保满足系统设计指标要求[4]。

目前的全球卫星导航系统星座可用性分析主要采用马尔科夫链[5]、贝叶斯网络[6]等分析方法，这些方法的优点主要体现在概念清晰，建模较为简单，可以得到系统的稳态特性，具有建模便利和求解快速的优点。但是，这些方法对实际问题做出了较多的简化和假设，存在以下不足：①对于卫星可靠性的变化，星座中不同卫星由于使用时间不同等导致的状态差异等问题描述不够精细；②星座状态转换方案比较复杂，例如各种情况下星座的备份策略、失效卫星的替换操作逻辑等在模型中体现不足；③导航星座在轨运行阶段备份主要分析卫星寿命期内系统在多约束条件下的状态变化，传统方法对这一变化过程难以分析，由此导致所给出的备份策略具有一定的局限性。

针对现有方法存在的不足，本文提出一种基于Petri网的Walker导航星座备份策略，首先，介绍了随机Petri网模型、卫星可靠性模型，定义了星座等级和星座可用性，明确了导航星座备份的设计要求；其次，以中轨道Walker星座为例，分别分析了无备份星时、仅考虑地面备份时以及考虑在轨和地面均备份策略时的星座可用性及备份卫星数目；最后，给出了Walker导航星座备份策略的算例。

2 星座备份分析模型

本节首先介绍了用于星座备份策略研究的随机Petri网模型和卫星可靠性模型，给出了卫星失效和可用、星座等级，星座可用性的定义，以及相应的导航星座备份策略的设计要求。

2.1 随机Petri网模型

一个Petri网由4部分组成：一个位置集合P，一个转移集合T，一个输入函数I和一个输出函数O。输入函数是一个从转移tj到为该转移的输入位置的集合I(tj)的一个映射，输出函数是一个从转移tj到为该转移的输出位置的集合O(tj)的一个映射[7]，图1给出了Petri网模型图。

图1 Petri网模型图Fig.1 Petri net model

图1中用圆圈表示位置，短竖线表示转移，从转移到位置的有向弧表示该转移的输出位置，从位置到转移的有向弧表示该转移的输入位置。

本文建立了基于面向对象Petri网的分析模型，其基本思路是将星座运行中的各类事件建立为Petri网的变迁，通过变迁描述系统状态在多约束条件下的变化过程。各类变迁的发生条件、发生时间按照实际系统运行情况建模，对于随机性的时间采用随机变量来模拟。随着时间的推进，即可以模拟真实系统中系统状态随时间的演变。导航星座备份考虑的关键不确定性因素如表1所示。

表1 导航星座备份考虑的关键不确定性因素

由于星座运行中包含大量的随机因素，这些因素在Petri网模型中都采用随机变量表示，因此模型实际上是一个随机Petri网。一次运行的结果反映了系统实际运行的一个可能结果，通过多次蒙特卡洛仿真，即可得到系统可能的运行结果集。对这些运行结果进行分析，统计星座设计关注的变量，可以得到变量的随机分布，从而完成对系统性能的统计分析。

随机Petri网模型考虑了系统运行的各种确定性因素(备份决策、运行逻辑等)和随机事件(卫星失效时间、修复时间等)，模拟系统的真实运行流程和事件发生概率进行推进。考虑的边界条件包括卫星可靠性、卫星操作维持平均间隔、卫星操作维持平均持续时间、可恢复故障平均间隔、可恢复故障平均修复时间、平均应急发射卫星时间、发射成功率、平均故障监测时间、轨道转移平均时间、轨道转移成功率、最大同时测试发射卫星数量，以及最大同时轨道转移数量等，这些边界条件均以变量的形式包含在模型中，并影响系统的演化，从而可以仿真不同备份策略下系统的运行响应。随机Petri网模型既可以分析系统在多约束条件下的变化过程，也可以分析系统的稳态特性。

2.2 卫星可靠性模型

卫星可靠性反映了卫星故障的概率。卫星在轨运行期间可能发生长期故障和短期故障，长期故障亦称不可恢复性故障，这种故障通常对卫星的影响是致命性的。发生这种故障的卫星通常不能被维修，只能等待发射新的卫星来替换。这里可靠性指卫星发生长期故障的概率，是影响星座备份策略的最主要因素。

假设卫星的设计寿命为10年，寿命末期单星可靠性优于0.65。一般均假设单星故障概率服从指数分布，卫星故障的概率正比于工作时间，由于卫星状态一致性非常好，同时假定卫星在寿命末期的可靠性为常数，那么10年寿命期间，卫星可靠性变化为

(1)

式中：a为卫星寿命末期的可靠性，假设为0.65；t为卫星的运行时间，取值为0～10年。L为卫星的设计寿命，取值为10。

根据式(1)，可得卫星寿命区间可靠性变化曲线，如图2所示。

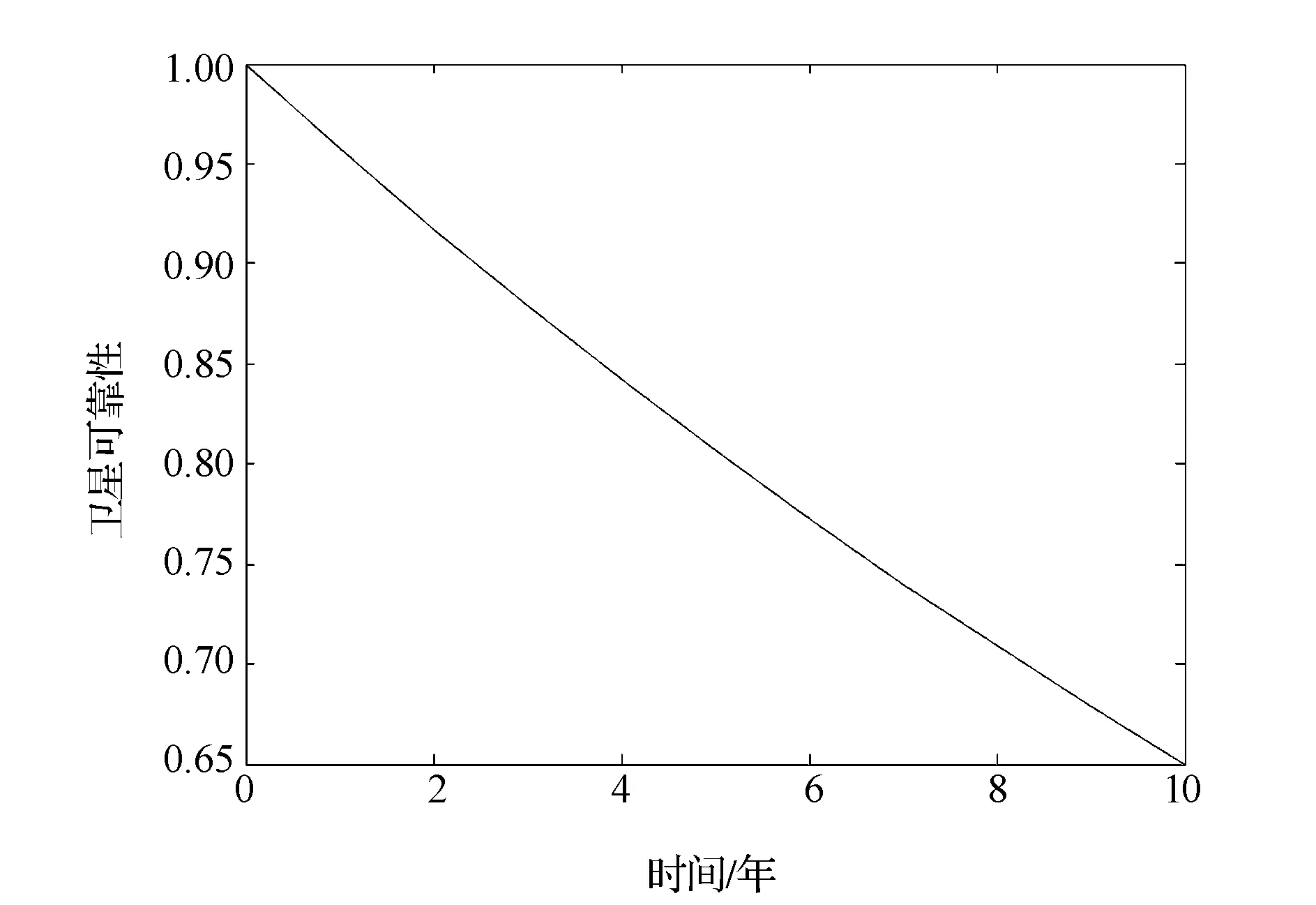
图2 导航卫星可靠性变化曲线Fig.2 Variation curve of reliability model for navigation satellite

由此可见，卫星成功发射后可靠性逐年降低。文献[6]改进了卫星可靠性指数分布模型，新模型采用了随机故障模型和损耗故障模型相乘的方法。

2.3 星座可用性定义

1)卫星失效和可用

影响卫星可靠性的因素可分为3种类型：长期故障，短期故障以及对卫星的运控操作调整。长期故障和短期故障的区别是，长期故障指灾难性的故障，需要地面发射一颗卫星来替换，而短期故障指那些可以通过软件重启、设备切换等进行维修后可以恢复正常工作的故障[8]。

(1)卫星失效：卫星出现长期故障。

(2)卫星有效：卫星未出现长期故障，可能出现过短期故障。

(3)卫星可用：卫星当前处于提供服务的状态。由于运控操作和短期故障的存在，部分有效状态的卫星也可能暂时无法提供服务，因此星座可用卫星数不大于有效卫星数。

2)星座等级

以构型参数为Walker 24/3/1:21528 km，55°星座为例，定义星座等级如下：

(1)R0：全部24颗卫星均有效，此时可以提供正常星座的全部性能；

(2)R1：至少23颗卫星有效；

(3)R2：3个轨道面上均至少有7颗星有效；

(4)R3：星座至少有21颗卫星有效。与R2相比，该等级可能出现同一轨道面有多颗卫星失效的情况；

(5)P0：全部24颗卫星均可用，此时可以提供正常星座的全部性能；

(6)P1：至少23颗卫星可用；

(7)P2：三个轨道面上均至少有7颗卫星可用；

(8)P3：星座至少有21颗卫星可用。

由于运行阶段各卫星的状态在不断变化，因此星座等级是随卫星状态不断变化的。显然，考虑到星座的维持操作及故障状态，P等级星座比R等级要求更严格。即当前时刻星座处于某P等级，则它一定处于对应的某R等级。注意等级定义中的卫星均指正常轨位卫星，不包括备份卫星。

3)星座可用性

星座可用性是指星座在规定的时间内，在规定的轨道位置提供健康卫星导航信号的概率，是在用户层面上反映星座工作状态的重要指标。本文将星座可用性定义为星座在一段时间内满足特定要求的时间比例。具体指时间T的星座可用性：从星座运行开始到T的时间内，星座达到构型等级(R0、R1、R2、R3、P0、P1、P2、P3)的时间占总时间的比例。根据选择星座构型等级的不同，分别定义为R0、R1、R2、R3、P0、P1、P2、P3可用性。由定义可知，星座可用性是时间T的函数，在整个运行过程中是动态变化的。

2.4 设计要求

星座备份策略设计的目的是保证星座寿命期内提供稳定的导航服务，具体要求为：在考虑星座可能发生故障、操作维护等情况下，导航系统整个服务区达到位置精度因子(Position Dilution of Precision，PDOP)PDOP<4的平均可用性大于95%[9-10]。根据星座设计论证计算结果，星座等级只要优于P3等级，均可以满足整个服务区达到PDOP<4的指标要求。因此，备份策略分析可确定最低要求为：在星座运行阶段，P3可用性优于95%。

P3等级下，星座只能保证可用卫星数目不少于21颗，仅能满足提供服务的最低要求。为留有余量，在分析中也对星座P2可用性进行了分析。考虑到R0等级为导航星座的标称状态，在运行阶段保持满星座运行也是期望的。因此可以选择R0可用性作为备份策略设计的最高要求。

P3等级仅能满足星座提供服务的最低要求，一旦无法满足，星座提供达到导航性能指标的可能性就会很低，因此星座备份策略设计必须保证运行阶段星座以很高的概率满足星座的P3等级优于95%的要求。为此提出第一个层次的要求：运行期间星座P3可用性优于95%的概率不低于98%。

同样P2、R0等级下系统服务指标还有一定冗余，即使星座暂时不能达到等级要求，依然可能提供导航性能，因此其概率要求可以有所降低。

因此定义星座备份策略的要求如下：

要求1：运行期间星座P3可用性优于95%的概率不低于98%；

要求2：运行期间星座P2可用性优于95%的概率不低于90%；

要求3：运行期间星座R0可用性优于95%的概率不低于70%。

3 无备份星时星座变化特性分析

如果不进行地面备份和在轨备份，星座初始仅24颗卫星在轨运行，卫星失效后不再补发。可以预计，随着运行时间的增长，星座的可用性将逐步下降。对星座运行情况进行1000次仿真，仿真结果反映了星座运行情况的1000次抽样，可以统计分析星座性能。任务时间取为10年。

每次仿真均会计算星座处于各等级的时间占整个运行时间的比例，即该次仿真运行得到的星座可用性，由于模型的随机性，各次运行的星座可用性是不一样的，服从一定的随机分布。根据大数定理，经过大量仿真，仿真结果均值会收敛于实际随机分布的数学期望。图3给出了无备份星时星座可用性收敛情况。

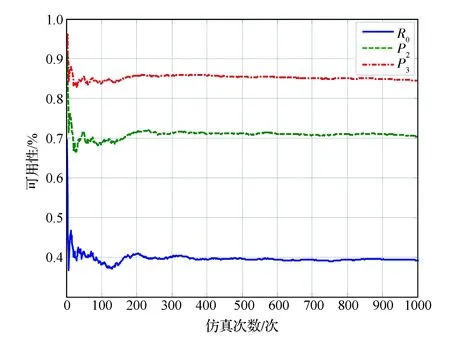
图3 无备份星时星座可用性均值随仿真次数的变化曲线Fig.3 Variation curves of mean constellation availability vs. simulation times for no spare satellites

图3中横坐标为仿真次数，纵坐标为仿真所得星座可用性的均值。由图3中可以看出，大约500次仿真后，R0、P2和P3三个可用性均趋于稳定。

表2给出了R0、P2和P3三个可用性的分布情况，表2中平均值表示所有运行得到的可用性的平均，反映了星座可用性的概率。最大值和最小值表示所有运行中得到的最大或最小结果，需要注意的是，三个可用性为独立统计的，所以最大可用性的3个结果可能不是同一次运行得到的。

由表2可以看出，无备份星时星座的可用性比较低，运行期间3个级别的平均可用性均小于85%，3个可用性的最大值均接近于100%。三个等级可用性大于95%的概率分别为0.8%、5.1%和28.3%，概率都不高。如果无备份措施，则无法满足星座性能要求，因此必须采用备份措施。

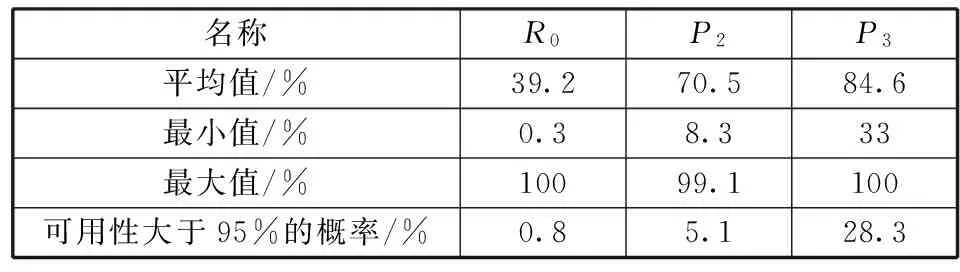
表2 无备份星时星座可用性分布情况

4 仅考虑地面备份策略分析

通过第3节分析可知，如果不采用备份措施，则无法满足设计要求。地面备份是指在有卫星失效的情况下进行发射补网，属于按需发射，因此同等条件下所需要的备份卫星数目最少，但是需要考虑应急发射时间、发射成功率等影响因素。这一策略下，星座初始仅24颗卫星在轨运行，卫星失效后由地面发射补充。

任务时间取为10年。根据第3节的仿真结果，大约500次仿真后，各统计特性基本趋于稳定，可以满足初步分析的要求，因此下面均仿真500次取样。假设地面备份运载火箭的数量足够，图4给出了仅考虑地面备份策略时星座可用性收敛情况。

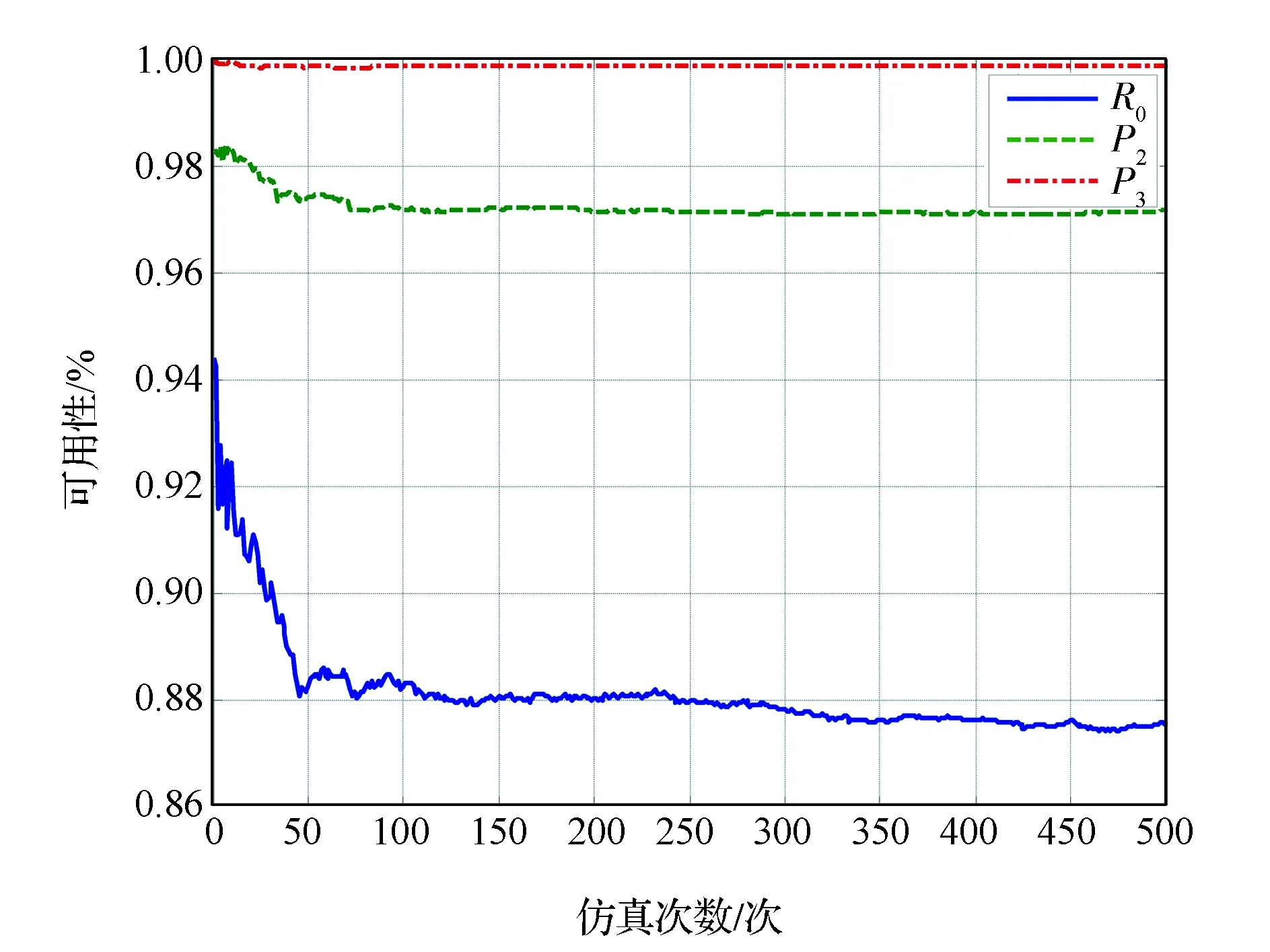
图4 仅考虑地面备份时星座可用性均值随仿真次数的变化曲线Fig.4 Variation curves of mean constellation availability vs. simulation times only for spare satellites on the ground

表3给出了R0、P2和P3三个可用性的分布情况。

由表3可知，在仅考虑地面备份策略下，R0、P2和P3可用性均值比无备份星时均有较大提高。但是R0可用性仍然偏低，均值仅有87.5%，可用性大于95%的概率只有13.4%，因此R0可用性指标不满足。而P2和P3可用性均较高，均值都达到95%以上。特别是P3可用性，所有仿真中均在98.2%以上，完全满足要求。而P2可用性优于95%的概率也比较大，达到91.8%。因此，在仅考虑地面备份的情况下，无法满足R0可用性的要求，可以满足P2、P3可用性的要求。

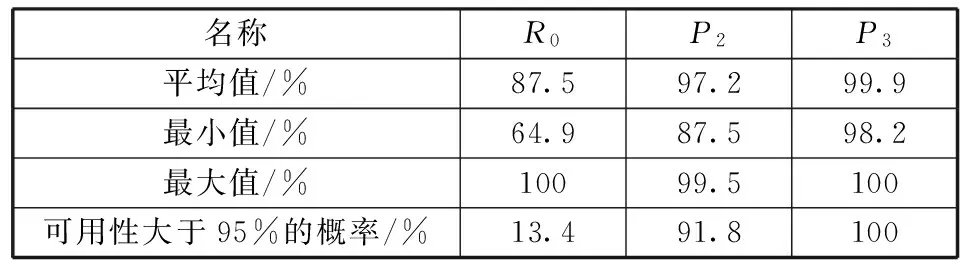
表3 仅考虑地面备份时星座可用性分布情况

上述分析未考虑备份卫星数目的限制，即认为备份卫星和运载火箭是充足的，在星座运行期间均可以满足发射需要。实际上星座运行期间可用备份卫星数目是有限制的，这会影响星座的可用性。下面重点分析地面备份星数目对星座可用性的影响。

针对备份星数目为1～9颗的情况分别仿真500次，进行可用性统计分析，可用性优于95%概率与备份卫星数目的关系如图5所示。

图5 星座可用性概率随备份星颗数的变化Fig.5 Variation curves of the probability of constellation availability vs.the number of spare satellites

由图5可以看出：①R0可用性满足指标要求的概率始终低于0.2，表明地面备份无法满足2.4节设计要求3；②如果要满足设计要求2，地面至少需要备份8颗卫星；③如果要满足设计要求1，地面至少需要备份7颗卫星。

5 在轨和地面均备份策略分析

在轨备份策略将备份卫星部署在工作轨道高度，在轨备份卫星只能替代同轨道面内的失效卫星。因此，要求至少每个轨道面部署一颗备份卫星。当星座出现故障卫星时，备份卫星只需要通过简单的相位调整就能够实现对故障卫星的替换，从而实现对星座性能的快速修复。如果将备份卫星融入到星座中，作为轨道面内故障概率最高的一颗工作卫星的伴随星，则当工作卫星出现故障时，备份卫星可以马上替换故障卫星工作，而星座性能并不会因为卫星故障而受到影响。同时，该部署方式可以有效地利用备份卫星来增强星座的服务性能。

下面针对在轨和地面均备份策略进行分析，当卫星失效时，如果同轨道面有备份卫星，则通过备份卫星轨道转移进行替换，如果同轨道面没有备份卫星，则由地面进行卫星补网发射。备份卫星替换正常卫星或者备份卫星失效后，再由地面进行补发。需要指出的是，在轨备份考虑对称部署方式，即对Walker星座每个轨道面均部署同样数目的备份卫星。

任务时间取为10年。首先假设地面备份星足够，分析在每个轨道面各备份1颗卫星时星座的性能，仿真500次(见图6)。

图6 对称部署下星座可用性收敛过程(每个轨道面各备份1颗)Fig.6 Convergence process of constellation availability for the symmetric deployment (One spare satellite on each orbital plane)

表4给出了R0、P2和P3三个可用性的分布情况。

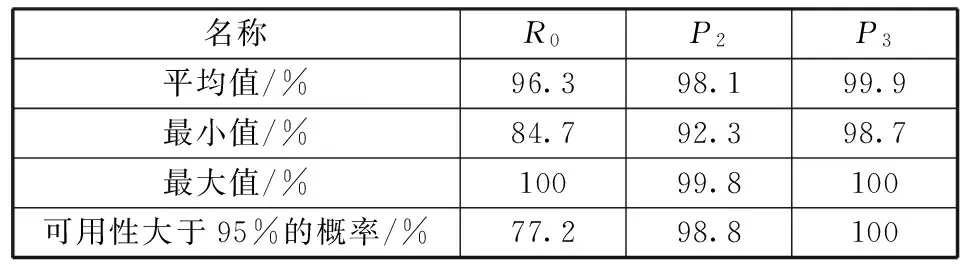
表4 对称部署下星座可用性分布情况(每个轨道面各备份1颗)

从图6和表4可以看出，在每个轨道面各备份1颗卫星的情况下，星座可用性有了大幅提高。星座P2、P3可用性均值分别为98.1%和99.9%，优于0.95的概率均超过98%，可以说完全满足了P2、P3可用性的要求。R0可用性的均值也达到了96.3%，优于95%的概率为77.2%。

表5给出了在每个轨道面各备份2颗卫星时，R0、P2和P3三个可用性的分布情况。

表5 对称部署下星座可用性分布情况(每个轨道面各备份2颗)

从表4、表5可以看出，在每个轨道面各备份2颗时，P2和P3的可用性提升并不明显，R0的可用性提升了9.6%。而且，同一轨道面同时失效两颗卫星的情况下，第二颗备份卫星才能起到作用，在其它情况下对星座的可用性与备一颗是一样的，因此不考虑每个轨道面各备份2颗卫星的情况。

针对每个轨道面各备份1颗卫星的情况，分别取地面备份卫星数目为0，3，6，7，8，9，10进行仿真计算，各种情况分别仿真500次，进行可用性统计分析。

图7给出了可用性优于95%概率与备份卫星数目的关系，图中粗线为在轨备份加地面备份方案，细线为仅采用地面备份方案。考虑到在轨卫星备份情况时有3颗在轨备份卫星，因此其备份卫星数目为地面备份卫星数目加3。

由图7可知，当备份卫星数目大于6时，在备份卫星数目一样的前提下，在轨备份方案在P2和P3可用性满足指标要求的概率与地面备份卫星相当或者稍高。在每个轨道面各备份一颗卫星的基础上，满足2.4节设计要求1，还需要地面备份3颗卫星；满足设计要求2，还需要地面备份5颗卫星；满足设计要求3，还需要地面备份7颗卫星。

综合备份卫星成本和系统运行的性能，对于Walker 24/3/1:21528 km，55°星座，假设设计寿命10年，每颗卫星的可靠性按指数规律衰减，末期可靠性为0.65，比较不同的备份方案。设计要求1可以较好地保证导航系统的服务性能。经过分析，在轨备份3颗卫星、地面备份3颗卫星时星座的可用性如下：R0的可用性均值为89.9%，P2的可用性均值为96.4%，P3的可用性均值为99.6%。可以看出，以上三种指标的性能能较好地满足要求。当一颗卫星失效后，由在轨备份星接替失效星，继续工作。同时，为该轨道平面发射地面备份星，系统继续平稳运行。

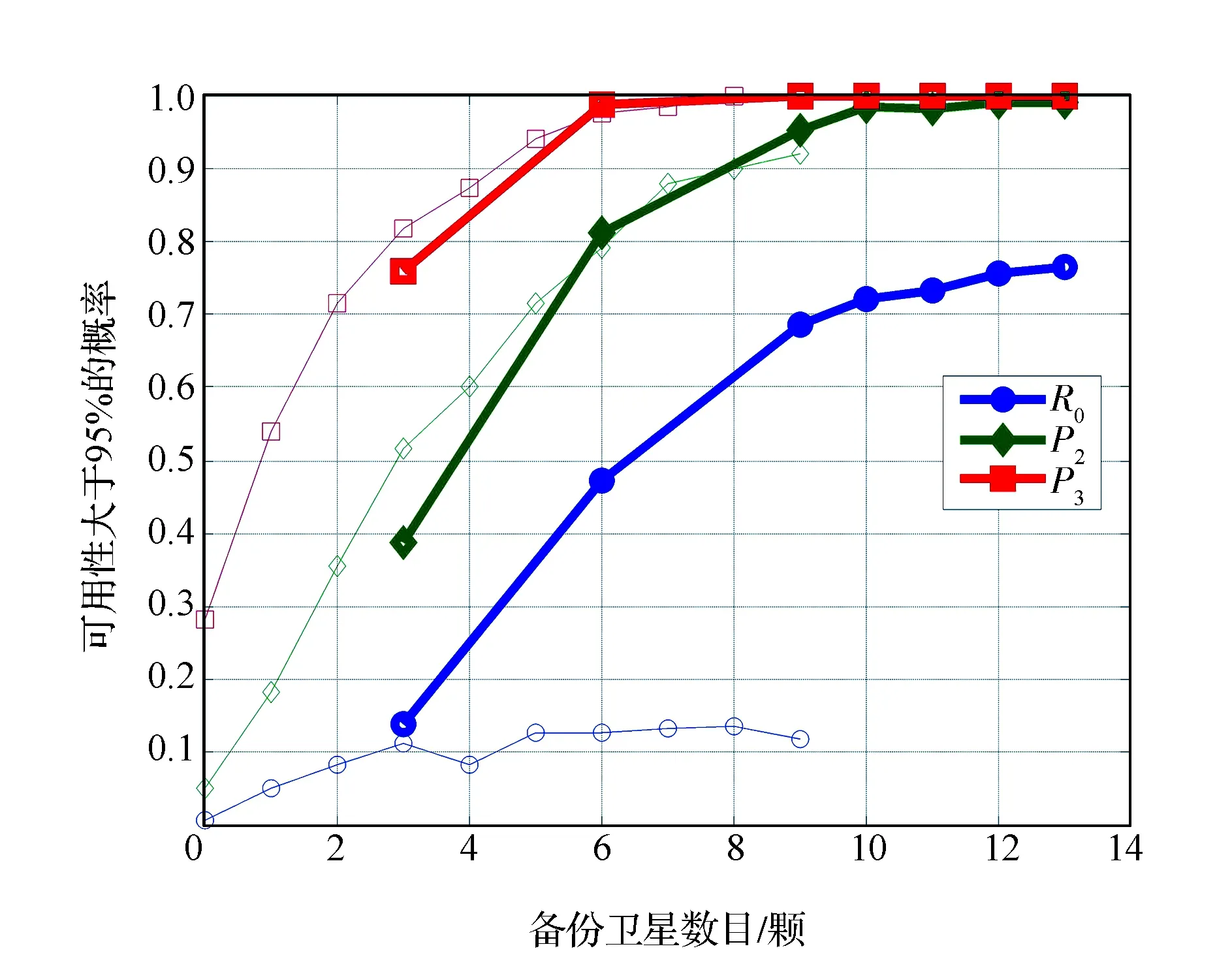
图7 星座可用性概率随备份卫星数目变化曲线Fig.7 Variation curves of the probability of constellation availability vs.the number of spare satellites

6 结束语

本文首先对Walker导航星座备份策略的设计要求进行了分析，提出了3个可用性等级和备份策略设计的3个定量指标要求。然后利用Petri网方法建立了星座运行阶段状态变化的多约束模型，星座中各颗卫星都作为独立的个体进行状态演化，模型考虑了卫星失效后的处置流程，使星座运行中包含大量随机事件，这些约束都按照真实系统的发生规律特点进行了模拟。提出的随机Petri网模型可以将星座的运行过程仿真，基于蒙特卡洛原理对星座可用性的随机分布情况进行了统计分析。在轨备份卫星可以部署在失效故障概率最大的卫星附近，当卫星失效后，直接利用在轨备份卫星替换失效卫星，并发射备份星至该轨道面。当工作星失效且没有同轨备份星时，由地面发射卫星至失效工作星轨位，并发射备份星至备份轨位。进一步的研究工作包括改进卫星可靠性模型，分析卫星寿命末期不同可靠性指标对星座备份卫星数目的影响。

References)

[1] Massatt P,Fritzen F. Assessment of the proposed GPS 27-satellite constellation[C]// ION GPS/GNSS 2003.Manassas,VA: Institute of Navigation,2003:399-406

[2]Massatt P,Fritzen F,Scuro S R,et al. A comprehensive trade study on GPS constellation size and number of orbit planes[C]//ION GNSS 19th International Technical Meeting of the Satellite Division.Manassas,VA: Institute of Navigation,2006:2139-2150

[3]Grimes J G.Global Positioning System standard positioning service performance standard[S]. Washington D.C.:Office of the Secretary of Defense,2008:9-12

[4]Ricardo Píriz,Belén Martín-Peiró，Miguel Romay-Merino. The Galileo constellation design: A systematic approach[C]//ION GNSS 18th International Technical Meeting of the Satellite Division. Manassas,VA: Institute of Navigation,2005:1296-1306

[5]Rhonda Slattery,Karl Kovach. New and improved GPS satellite constellation availability model[C]//ION GPS 1999. Nashville: Institute of Navigation,1999:2103-2112

[6]Li Haisheng,Zheng Heng,Wang Wei,et al. Research on spare satellites strategy of navigation constellation based on system availability[C]//China Satellite Navigation Conference (CSNC) 2013 Proceedings.Beijing:China Satellite Navigation Office,2013:293-304

[7]洪志国.基于随机Petri网模型的卫星网络性能分析研究[D].北京：中国科学院，2004:33-44

Hong Zhiguo.Research on stochastic Petri nets-based performance analysis of satellite networks[D].Beijing: Chinese Academy of Science,2004:33-44 (in Chinese)

[8]蔡洪亮，李星. 基于服务可用性的导航星座薄弱环节分析[EB/OL].[2016-11-15]. http://d.g.wanfangdata.com.cn/Conference_8194348.aspx.

Cai Hongliang,Li Xing. Weakness analysis of navigation constellation based on service availability[EB/OL]. [2016-11-15]. http://d.g.wanfangdata.com.cn/Conference_8194348.aspx (in Chinese)

[9]郑典循,林合同,李琦,等. 导航星座快速补网轨道设计[EB/OL]. [2016-11-15]. http://d.g.wanfangdata.com.cn/Conference_8762223.aspx.

Zheng dianxun,Lin Hetong,Li Qi,et al. Desigh on the orbit transfer of rapid replenishment for navigation constellation[EB/OL].[2016-11-15].http://d.g.wanfangdata.com.cn/Conference_8762223.aspx( in Chinese)

[10] 陈志鹏，胡彩波，刘昌洁，等. 基于系统服务性能提升的北斗卫星备份星轨位方案分析[EB/OL].[2016-11-15]. http://d.g.wanfangdata.com.cn/Conference_8761983.aspx

Chen Zhipeng,Hu Caibo,Liu Changjie,et al. Analysis of BDS backup satellite orbit plan based on system service performance enhancement [EB/OL].[2016-11-15]. http://d.g.wanfangdata.com.cn/Conference_8761983.aspx (in Chinese)

(编辑：李多)

郑 重 声 明

最近不断有作者向编辑部反映，收到以《航天器工程》期刊编辑的名义收取“审稿费”、“版面费”等费用的信函或邮件。

对此，《航天器工程》郑重声明：本刊一直以来在办刊过程中不向作者收取任何费用，本刊没有授权任何个人或组织来代理稿件受理事宜，任何与《航天器工程》投稿有关收费的网站、网页均为诈骗性质的，一切以本刊名义向作者收取费用的行为均为诈骗行为，本刊保留通过法律渠道追诉的权利。请广大作者明鉴，以防上当受骗。有关投稿事宜和举报电话，参见期刊封底联系方式，请直接与编辑部联系。

谨此启示。

《航天器工程》编辑部

2017年4月2日

Research on Spare Strategy of Walker Navigation Constellation Based on Petri Net

HU Min SONG Xumin YANG Xuerong

(Equipment Academy of PLA,Beijing 101416，China)

This paper proposes a spare strategy of Walker navigation constellation based on Petri net. The strategy considers the main uncertain factors during the operation phase of navigation constellations. The obtained space strategy based on the proposed approach can make the real operation of navigation constellations be very close to the expected constellation availability. The Walker 24/3/1:21528 km，55°is taken as an example,the following three scenarios are analyzed: the first scenario is with no spare satellite,the second scenario is only with the spare satellites on the ground,and the third scenario is with both on-orbit and on the ground spare satellites. The results of analysis indicate that with three spare satellite on orbit and three spare satellites on the ground can guarantee the steady operation of navigation constellation,which can provide some references for the spare strategy selection of Walker navigation constellation.

Walker navigation constellation；Petri net；on-orbit spare；on the ground spare；constellation availability

2016-11-17；

2016-12-29

胡敏，男，博士，从事卫星导航系统星座设计研究。Email：jlhm09@163.com。

P228

A

10.3969/j.issn.1673-8748.2017.02.003