分式极限的计算方法初探

郝连军

辽宁石化职业技术学院

分式极限的计算方法初探

郝连军

辽宁石化职业技术学院

《高等数学》是高职学生最重要的基础课之一，高职学生《高等数学》学习的好与坏直接关系到专业课的学习成败，而《高等数学》中第一章极限知识掌握的好与坏直接关系到《高等数学》后续课程学习的成败。对于初学者分式函数极限的求法是比较困难的，如何解决这一难点，帮助学生顺利的完成函数极限知识的学习非常关键。下面通过实际的教学经验总结分式极限计算的几种求法，以便学生更好的掌握这一部分知识。

函数极限；分式极限；计算方法

一、利用分式极限的运算法则求极限

当分式的分母不为零时，可用极限的运算法则求极限

所以

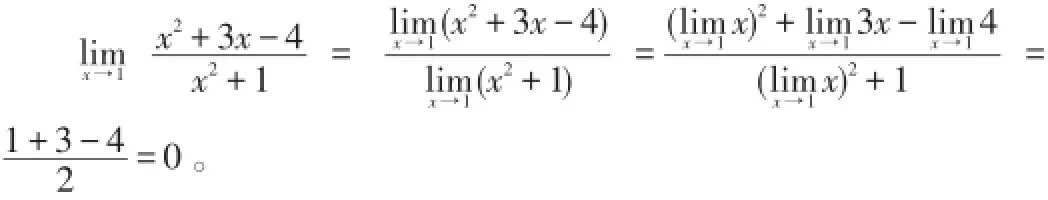
二、因式分解法求极限

如果分式的分子、分母有零因子的公因式，消去零因子，使函数转化为能用法则求极限的形式。

解：此极限x+2为零因子公因式，所以

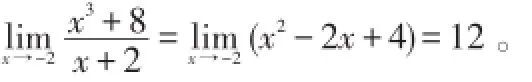
三、倒数法求极限

如果分式的分子极限不为零，而分母的极限为零，极限的运算法则不能用，则取倒数求极限，根据无穷小与无穷大的关系，求出原函数的极限。

四、分子有理化法求极限

先有理化，再消掉极限为零的因子再求极限。

解：

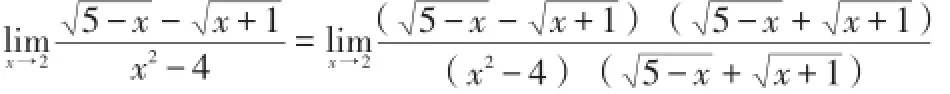
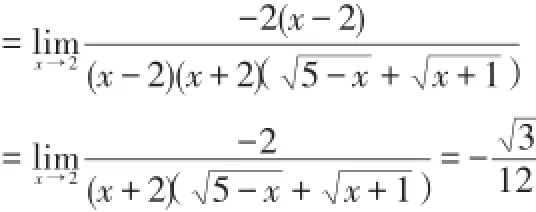
五、利用重要极限求极限

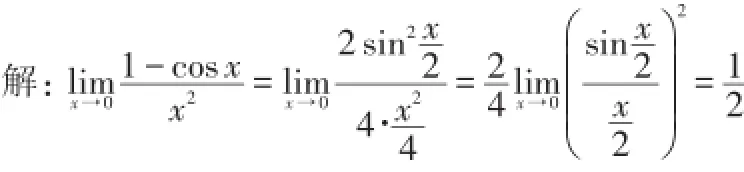
六、利用等价无穷小代换求极限

当x→0时，下列函数都是无穷小（即极限是0），且相互等价，即有：

x～sin x～tan x～arcsin x～arctan x～ln(1+x)～ex-1。

如果函数f(x),g(x),f1(x),g1(x)都是x→x0时的无穷小，且且等于

∵当x→0时，sin x～x arcsin x～x

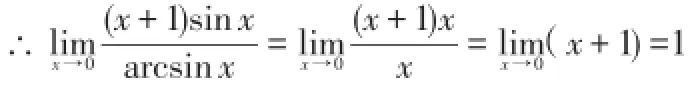
七、利用洛必达法则求极限

（2）f(x)和g(x)在点x0的左、右近旁均可导，且g′(x)≠0；

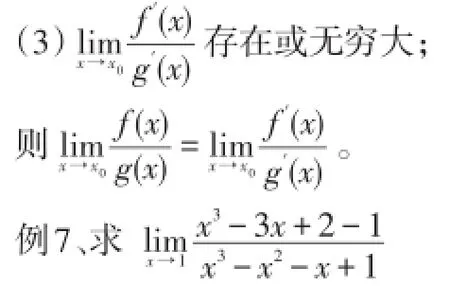
解：由洛必达法则得

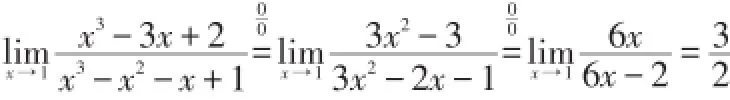
八、两边夹法则求极限