M6断块中低孔隙度渗透率砂岩储层饱和度模型优选方法

尹军强,赵毅

(中石化华东石油工程有限公司地质测井处,江苏 扬州 22500)

0 引 言

准确计算含水饱和度是中低孔隙度渗透率储层定量评价的难题之一。在阿尔奇公式中岩电参数的影响因素和求取方法也被不同程度地归纳总结,比如在温度、压力、孔隙结构系数以及地层水矿化度等影响方面都做了大量的研究工作[1-8]。但是,当孔隙结构复杂,地层因素和孔隙度不再表现为阿尔奇线性关系特征的时候,岩电参数是否还是定值,或者从孔隙特征当中,还有哪些因素对岩电参数有很大影响,这时候Archie公式能否能够继续适用储层的饱和度计算,又或者有没有别的方法更适用于中低孔隙度渗透率储层的饱和度求取。本文鉴于上述的问题,一方面在阿尔奇公式中,引入无效导电孔隙[9],从岩电参数的物理意义中考察其间的相互关系,求取岩电参数。另一方面基于等效岩石组分理论对岩石导电性的影响,探讨EREM模型对于中低孔隙度渗透率砂岩储层的饱和度计算的适用性。

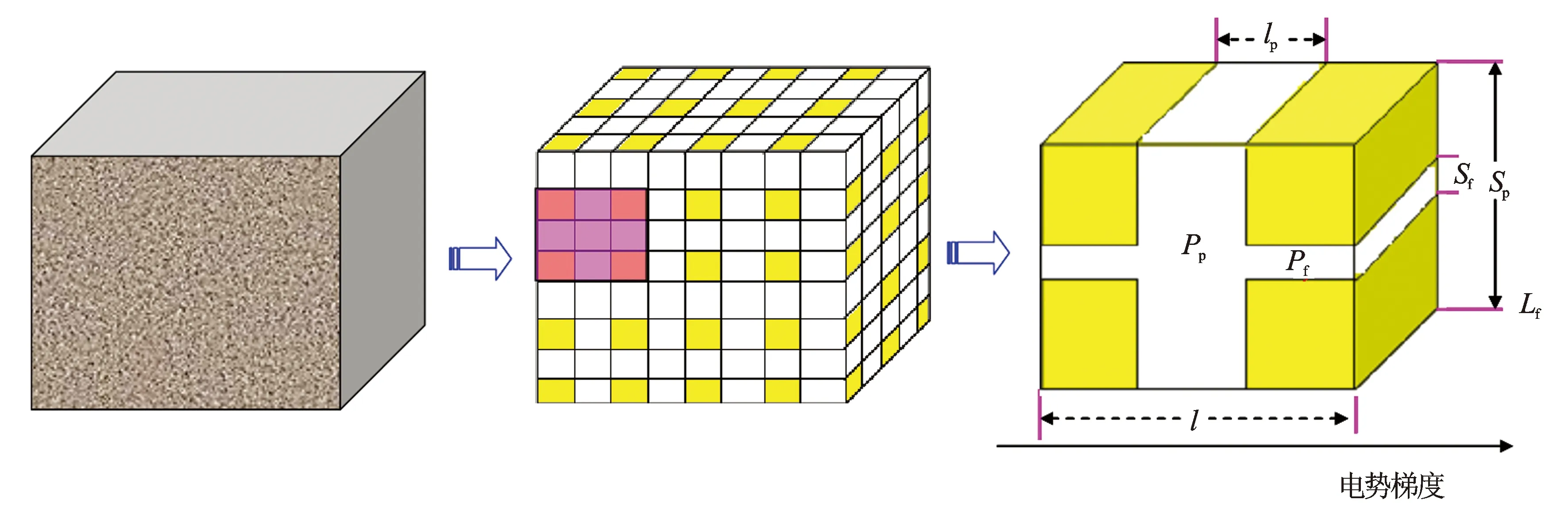
图1 等效岩石组分模型示意图

选取苏北盆地金湖凹陷西斜坡带中段的M6断块砂岩储层为研究对象,储层岩性是细砂岩和含粉砂细砂岩,以钙质胶结和泥质胶结为主,泥质含量分布在6%～12%,泥质含量较少,孔隙度变化范围10.70%～24.30%,平均16.10%,渗透率变化区间(2.90～251.80)×10-3μm2,平均40.80×10-3μm2,属于中低孔隙度中低渗透率储层。

1 含水饱和度解释方法

1.1 Archie公式

1942年,Archie在大量试验研究基础上建立了粒间孔隙砂岩电阻率与孔隙度、含水饱和度之间的试验关系

(1)

(2)

两式联立,得

(3)

式中,R0为100%饱含地层水的岩石电阻率,Ω·m;Rw为地层水电阻率,Ω·m;Rt为岩石的电阻率,Ω·m;F为地层因素,无量纲;I为电阻率增大率,无量纲;φ为孔隙度,小数;Sw为含水饱和度,小数;a、b、m、n为岩电参数,a、b为岩性系数,无量纲;m为胶结指数,无量纲;n为饱和度指数,无量纲。

该公式假设地层是不含泥质和其他导电矿物的高孔隙度高渗透率纯岩石,岩石骨架基本不导电,岩石的导电性取决于连通孔隙中的地层水。通常利用Archie公式确定储集层含油气性时,a、b、m和n在某一层位取为固定值。由于实际地层与Archie公式假设的地层有一定的差别,尤其对于含中高泥质、孔隙度和渗透率都很低的地层,孔隙结构的复杂化使岩石参数取值范围变大,并降低了电阻率测井对流体类型的分辨能力,影响含油饱和度的正确求取。

1.2 基于等效岩石组分理论的饱和度模型(EREM模型)

基于等效岩石组分理论的饱和度模型适用于泥质较少的储层,在等效岩石组分理论中[10],将整个岩石等效为多个网格单元,对于每个网格单元,孔隙空间被划分成2个正交的组分(见图1)。组分Pf平行于电势梯度,而组分Pp垂直于电势梯度。对于每个组分体积,组分Pf的离子迁移效率远比组分Pp高,Pf与Pp的体积比定义为孔隙结构效率C。

依据孔隙结构效率和孔隙度的定义,结合图1可以得到孔隙结构效率C和孔隙度的表达式

(4)

(5)

式(4)和式(5)联合求解,可得

(6)

(7)

由于饱含水岩石由骨架和孔隙空间流体并联导电,则可得如下表达式

(8)

依据地层因素F的定义,式(8)可以转化为

(9)

联合式(6)、(7)和(9),可得地层因素的表达式为

(10)

式中,Vf为元素Pf占孔隙空间的体积;Vp为元素Pp占孔隙空间的体积。

假如不导电的油(气)规则地分布在2种元素中,那么Pwp和Pwf的体积将成比例的减小。由于受孔隙大小、连通性、流体性质及润湿性等因素影响,油(气)并不是规则分布。为了获取在含水饱和度Sw下的地层因素Fw,假设Vf=C,则Vp=1;假设赋存在元素Pf的含水饱和度为rSw,r为比例因子。

依据上述假设,则Pwf的体积Vwf可以表示为

Vwf=CrSw

(11)

由于Vwf+Vwp=(1+C)Sw,则

Vkp=(1+C)Sw-CrSw=[1+C(1-r)]Sw

(12)

依据式(11)和式(12),则修正后的孔隙结构效率Cw为

(13)

比例因子r表示水在2种元素的分布状态,一般与含水饱和度存在一定的关系

(14)

依据图2,可知水占据的孔隙度为φSw,依据式(10),含水饱和度Sw下的地层因素Fw为

(15)

当孔隙介质含有2种或2种以上流体相时,相的分布和存在状态是十分复杂的,并且受控于很多因素,如界面张力、颗粒的润湿性、孔隙尺寸、连通性等。在饱含多相流体的孔隙介质中,导电相必须具有一定的含水饱和度,才能导电。这最小的饱和度常常被称为临界饱和度(导电阀值),研究证实,这部分水往往存在于死孔隙中和被油湿岩石中的油包裹。

一种考虑最小导电饱和度影响的方法是成比例缩小含水饱和度,转为有效导电含水饱和度

(16)

2 关键参数的变化规律及求取方法

2.1 岩样选取

选取A井和B井不同物性的19块砂岩样品进行室内高温高压岩电实验测试,分析实验结果。

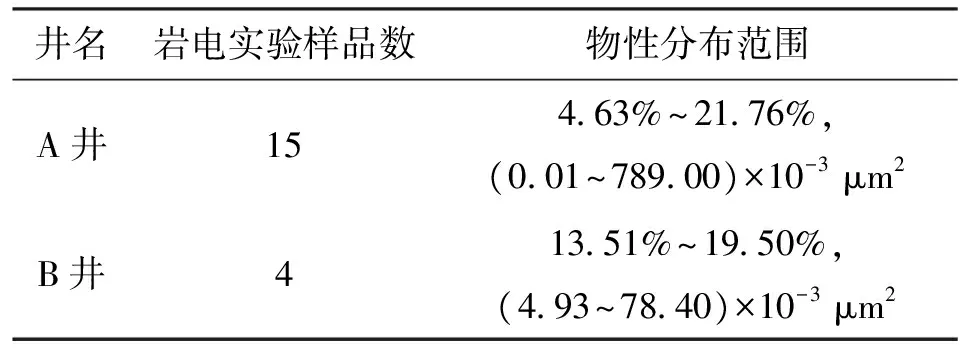
表1 实验样品清单(温度80 ℃,压力20 MPa)

2.2 岩电参数的变化规律及求取方法

(1) 岩电参数为固定值时求取方法。图2是地层因素与孔隙度的关系。从图2可见,当孔隙度小于12.9%的时候,地层因素与孔隙度呈发散现象,且孔隙度越小,地层因素规律性越差,其原因主要是在地层水矿化度较低时,相对于纯砂岩,泥质含量的增加改变了只有孔隙水导电的机理,造成低孔隙度低渗透率岩石的导电性增强,地层因素偏低。当孔隙度大于12.9%的时候,地层因素与孔隙度呈现较好的幂指数关系。

图2 地层因素与孔隙度的关系

基于岩石物理分析,讨论m的确定方法。由式(1)可知,若令a=1,得到m=-logF/logφ,即m为这组实验数据过原点直线斜率的绝对值,由此可以得出m为1.539 4。若令a不等于1,m可以通过图2中F—φ的幂指数关系的系数确定,a为3.938 9,m为0.934 0。而b和n通过电阻率增大系数与含水饱和度的关系确定,b为1.019 1,n为1.653 0。

(2) 岩电参数取变量时求取方法。从F—φ关系中可以得出,岩电参数m在孔隙度的变化中并不是恒定的,如果要想准确求取m值,需要针对m的物理意义重新思考途径。Wempe[11]和Candelario[12,13]认为岩石的总孔隙包括无效导电孔隙和有效导电孔隙,对于物性不好的砂岩储层或者致密储层,由于储层分选差、孔隙结构复杂,造成储层中存在一定的对岩石导电性几乎无贡献的孔隙,虽然这种无效导电孔隙度很小,但是对于孔隙度低于15%以下,特别是10%以下的储层,其对岩石导电性的影响不可忽略。换而言之,从胶结指数m的物理意义来说,它与无效导电孔隙存在着一定的关系。因此,根据Maxwell(1954)提出的地层因素与有效导电孔隙的关系,即

(17)

式中,φf为孔隙度,小数。

通过19块样品的孔隙度和地层因素,结合式(1)和式(17),就可以得到有效导电孔隙和无效导电孔隙。从图3上可以得出无效导电孔隙与胶结指数m之间的关系,单相关性达到了0.9以上,说明利用无效导电孔隙求取m更可行。孔隙度可以通过实验室直接测量得到,有效导电孔隙可以通过孔隙度计算得到。这样,就得到了当a为1时,通过孔隙度转换求取的m的关系,即

m=0.2062ln (0.5368φ+0.0072)+2.1732

(18)

图3 m与无效导电孔隙之间的关系

2.3 EREM模型中参数的变化规律及求取方法

利用19块岩电实验测量的数据,结合式(10)计算出每块样品的孔隙结构效率指数C,C趋近于0.278。然后通过式(13)至式(16)采用遗传算法,可以求取每块岩样的比例系数k和临界饱和度Swc,其中临界饱和度Swc绝大部分的数据点趋向于0.10,比例系数k与孔隙度呈单调递减的关系,相关性较好,单相关在0.88以上,可以利用孔隙度计算出比例系数k。

3 应用效果分析

通过关键参数的求取,结合孔隙度和电阻率曲线,即可得到Archie公式、变参数Archie公式以及EREM模型这3种方法计算的饱和度结果。为了突显哪种方法更接近实际地层情况,本文另外选取M地区试油层段为油层的C井和D井的18个岩心点作为对比对象。该地区没有密闭取心的饱和度资料,因此,引用该地区核磁共振实验得到的束缚水饱和度验证3种方法计算含水饱和度的准确性。

图4是C井3种方法处理的含水饱和度与岩心分析的束缚水饱和度对比的杆状图。该井20号层至26号层合层试油,日产油30.9 t,试油结论为油层。从图4可见,相比Archie公式、变参数Archie公式计算的含水饱和度,利用EREM模型计算的含水饱和度与油层段的束缚水饱和度更接近,而Archie公式、变参数Archie公式计算的含水饱和度偏大。

图4 C井1 975～2 020 m段处理成果图

图5是在C井和D井油层段中,Archie公式、变参数Archie公式以及EREM模型分别计算的含水饱和度与束缚水饱和度的比较。从图5可见,EREM模型计算的含水饱和度基本落在与束缚水饱和度对角线45°线的两边,变参数Archie公式计算的含水饱和度略好于Archie公式计算的结果。从表2中统计的3种方法计算的含水饱和度与束缚水饱和度的绝对误差上可以看出,常规阿尔奇公式计算结果的绝对误差在9.41%,沿用常规阿尔奇公式会造成流体解释的误判。相比之下,EREM模型计算结果的绝对误差在5.57%,变参数Archie公式计算结果的绝对误差在8.91%。由此可见,EREM模型计算结果最接近实际,换而言之,相比较变参数Archie公式和Archie公式,EREM模型更适用中低孔隙度渗透率砂岩储层的饱和度计算。

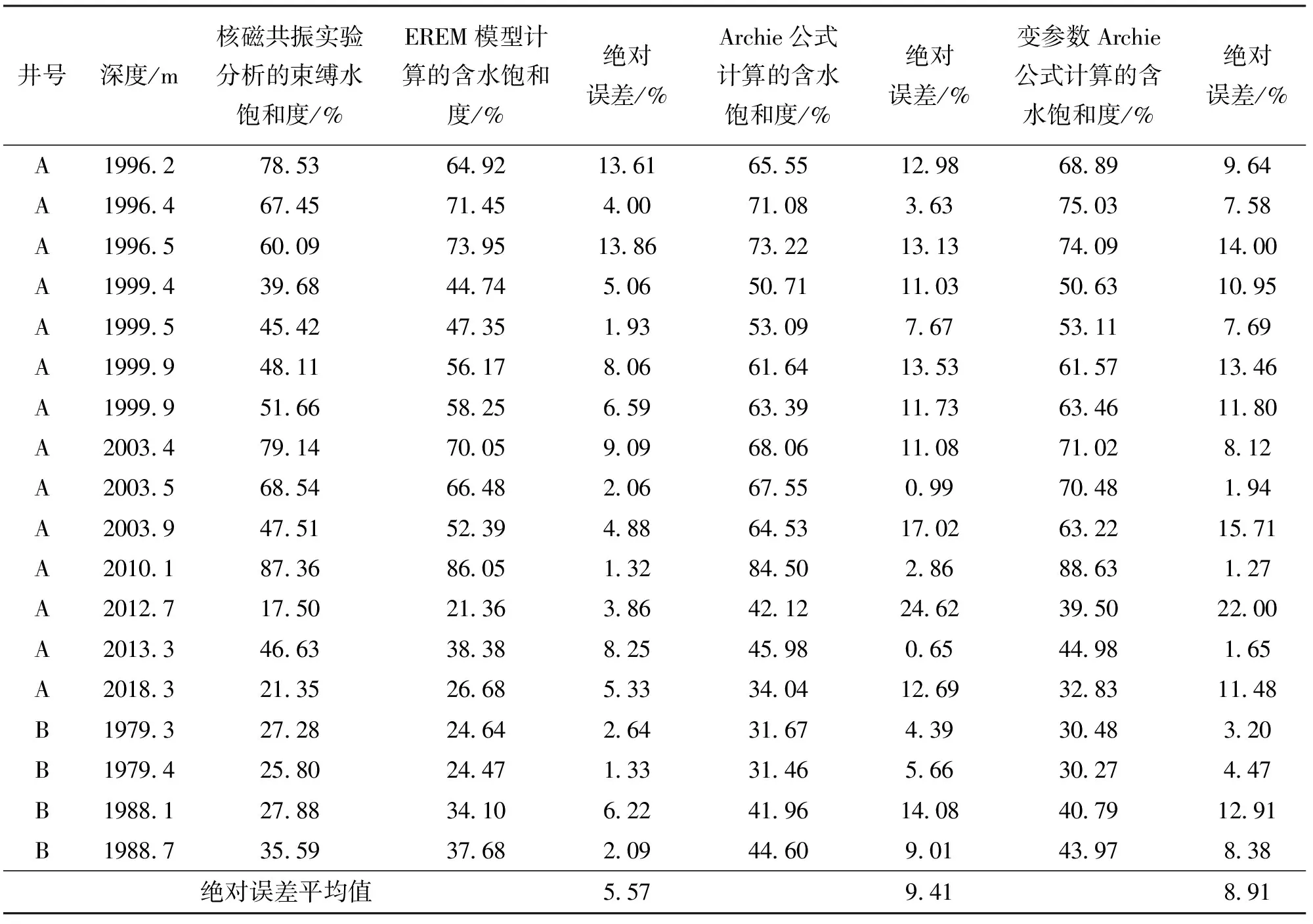
表2 2口井油层段3种方法计算的含水饱和度与束缚水饱和度的对比以及误差分析

图5 3种方法计算的含水饱和度与束缚水饱和度在油层段的比较

4 结 论

(1) 当砂岩储层中F—φ关系不满足Archie线性关系时,岩电参数不能像纯砂岩一样采用固定的参数,应根据储层特征进行调整。

(2) 在对胶结指数m进行讨论时,无效导电孔隙与m有很好的相关性,相比m取固定值,准确求取m可以提高含水饱和度的精度。

(3) 通过实验数据和试油资料验证,3种方法中,EREM模型计算的结果最好,能更好地描述中低孔隙度渗透率储层岩石的导电规律,提高该类储层饱和度的解释精度。

参考文献:

[1] ARCHIE G E. The Electrical Resistivity Log as an Aid in Determining some Reservoir Characteristics [J]. PetroleumTransactions,AIME,1942,146: 54-62.

[2] MARC F,KHOLOUD A N,DOUG B. Water Saturation from NMR,Resistivity and Oil Base Core in a Heterogeneous Middle East Carbonate Reservoir [C]∥SPWLA 46th Annual Logging Symposium,2005.

[3] 李奎周,范宜仁,王晓畅,等. 南堡凹陷复杂砂岩储层含水饱和度模型的研究 [J]. 测井技术,2009,33(3): 253-256.

[4] 张明禄,石玉江. 复杂孔隙结构砂岩储层岩电参数研究 [J]. 测井技术,2005,29(5): 446-448.

[5] 王勇,章成广,李进福,等. 岩电参数影响因素研究 [J]. 石油天然气学报,2006,28(4): 75-77.

[6] 罗娜. 阿尔奇公式数值分析及其意义 [J]. 石油学报,2007,28(1): 111-114.

[7] 刘兴礼,张贵斌,吉云刚,等. 塔中礁滩型碳酸盐岩储集层测井评价技术 [J]. 新疆石油地质,2011,32(3): 321-324.

[8] 李雄炎,秦瑞宝,刘春成,等. 岩电参数对储层饱和度计算精度的影响分析 [J]. 西南石油大学学报(自然科学版),2014,36(3): 68-72.

[9] 宋延杰,张啸,宋杨,等. 基于无效导电孔隙概念的致密砂砾岩有效介质导电模型 [J]. 地球物理学进展,2014,29(1): 209-216.

[10] SHANG B Z,HAMMAN J G,CALDWELL D H. A Physical Model to Explain the First Archie Relationship and Beyond [C]∥SPE Annual Technical Conference and Exhibition,Denver,Colorado,USA.,5-8 October,2004,4.

[11] WEMPE L W. Predicting Flow Properties Using Geophysical Data: Improving Aquifer Characterization [D]. Palo Alto: Stanford University,2000: 33-48.

[12] CANDELANO P R. Generalization of the Maxwell Won for Formation Resistivity Factors [J]. J Pet Tech,1976,28(7): 819-824.

[13] CANDELANO P R. On the Relationship Between Formation Resistivity Factor and Porosity [J]. Society of Petroleum Engineers Journal,1982,22(4): 531-536.