温度对HTPB推进剂疲劳特性的影响

梁 蔚, 吕庆山, 陈 雄, 许进升, 童 心, 闫晓晶

(1. 南京理工大学机械工程学院, 江苏 南京 210094; 2. 中国兵器工艺导航与控制技术研究所, 北京 100089; 3. 晋西工业集团技术研发中心, 山西 太原 030027)

1 引 言

端羟基聚丁二烯(HTPB)推进剂从浇铸到服役过程中受到如温度变化、飞行过程中弹体振动、运输振动以及海浪摇摆环境等引起的交变载荷[1]。这些交变载荷短时间内不会对药柱造成破坏,但长时间循环作用,会对推进剂的性能造成不良影响,最终导致发动机工作异常。因此,研究不同温度下HTPB推进剂的疲劳特性对了解药柱损伤和寿命评估有很好的参考意义。目前,国内外对材料疲劳特性的研究方法基本可以分为三类: 断裂力学法、唯象学法和耗散能法。断裂力学法通过检测裂纹的张开尺寸并计算裂纹尖端的应力强度因子来研究疲劳[2]。这种方法局限性是试验设备复杂并且应力强度因子在高温下不是常数。唯象学法通常研究损伤对材料宏观力学性能的影响以及材料损伤演化的过程和规律[3]。A.D. Drozdov[4]对高密度聚乙烯进行不同温度下的疲劳试验,建立了用残余应变表征的疲劳损伤模型; A.Launay[5]和W.Van Paepegem[6]用剩余强度和剩余刚度耦合的方法建立了考虑初始段循环软化的纤维增强材料的损伤演化模型。高艳宾等[7]建立了应变控制下NEPE推进剂的疲劳损伤演化模型,并分析了疲劳过程中颗粒的“脱湿”和损伤的发展。李金飞等[8]对定应变HTPB推进剂333 K和343 K振动载荷作用下的宏观力学性能变化规律和细观损伤模式进行了研究。耗散能法是近年来研究疲劳损伤较新的方法,物理含义为应力应变滞回曲线所围成的面积[9]。刘著卿[10]和王玉峰[11]等发现应变幅值决定了颗粒与基体之间的“脱湿”并且基于耗散能分析了其在载荷作用下的耗散特性; 王海波[12]等计算了交变温度作用下固体推进剂的耗散能和累积损伤因子,得到了不同载荷条件下的耗散能和累积损伤值; 曲凯[13]和邓斌等[14]基于不可逆能量耗散原理,建立了固体推进剂累积损伤模型并对发动机药柱累积损伤和使用寿命进行了分析。

总之,目前对交变温度下定应变老化过程力学性能的改变研究的较多,对于疲劳振动时温度影响的研究比较少。本研究进行了不同温度下相同应力加载作用的HTPB推进剂疲劳试验,分析了温度对疲劳寿命等参数的影响并建立了含温度效应的损伤演化模型。

2 试验与结果分析

2.1 试件的制备

试验用HTPB推进剂是三组元复合推进剂,组成为: 铝粉(Al)17%,高氯酸铵(AP)70%,基体HTPB橡胶及其他组分13%。由于HTPB推进剂极易受到湿度的影响,原始的方形板状材料都保存在干燥箱里。试验前用模具将原材料压制成15 mm×5 mm×5 mm的试件,然后使用环氧树脂胶将HTPB推进剂试样上下两端和铝制夹头粘接,再通过夹头与试验机夹具联接。试件的尺寸和与夹头的粘接方式见图1。试件制作完成后静置30 min使胶充分固化,然后放入温度为343 K保温箱中保温48 h。

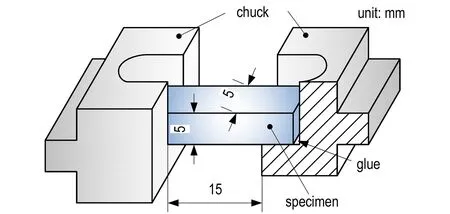
a. schematic graphics

b. physical graphics

图1 HTPB推进剂试件

Fig.1 HTPB propellant specimen

2.2 试验过程

疲劳试验在动态热机械分析仪(DMA,美国BOSE公司ELF3200)上进行,如图2所示。该系统能实现精确的位移和力控制,可确保设定疲劳载荷的准确性和稳定性; DMA的工作频率范围为10-5～200 Hz,温度控制装置可实现的温度范围为123～588 K,精度可达到±1 K。

图2 疲劳试验装置

Fig.2 Fatigue test device

疲劳试验采取的是应力控制脉动正弦波循环加载,由于HTPB推进剂的粘弹态温度范围是173～373 K,运输、贮存等服役环境的频率为0.1～50 Hz,考虑到较小的应力疲劳加载会使材料断裂。因此,频率定为20 Hz,温度设置为213,233,253,273,293,313,333 K,上限应力σmax取0.4 MPa(低于屈服应力0.7～0.8 MPa),下限应力σmin为0,周期t=1/f,每个温度下的疲劳加载试验重复3次,总共21个试件,如图3所示。

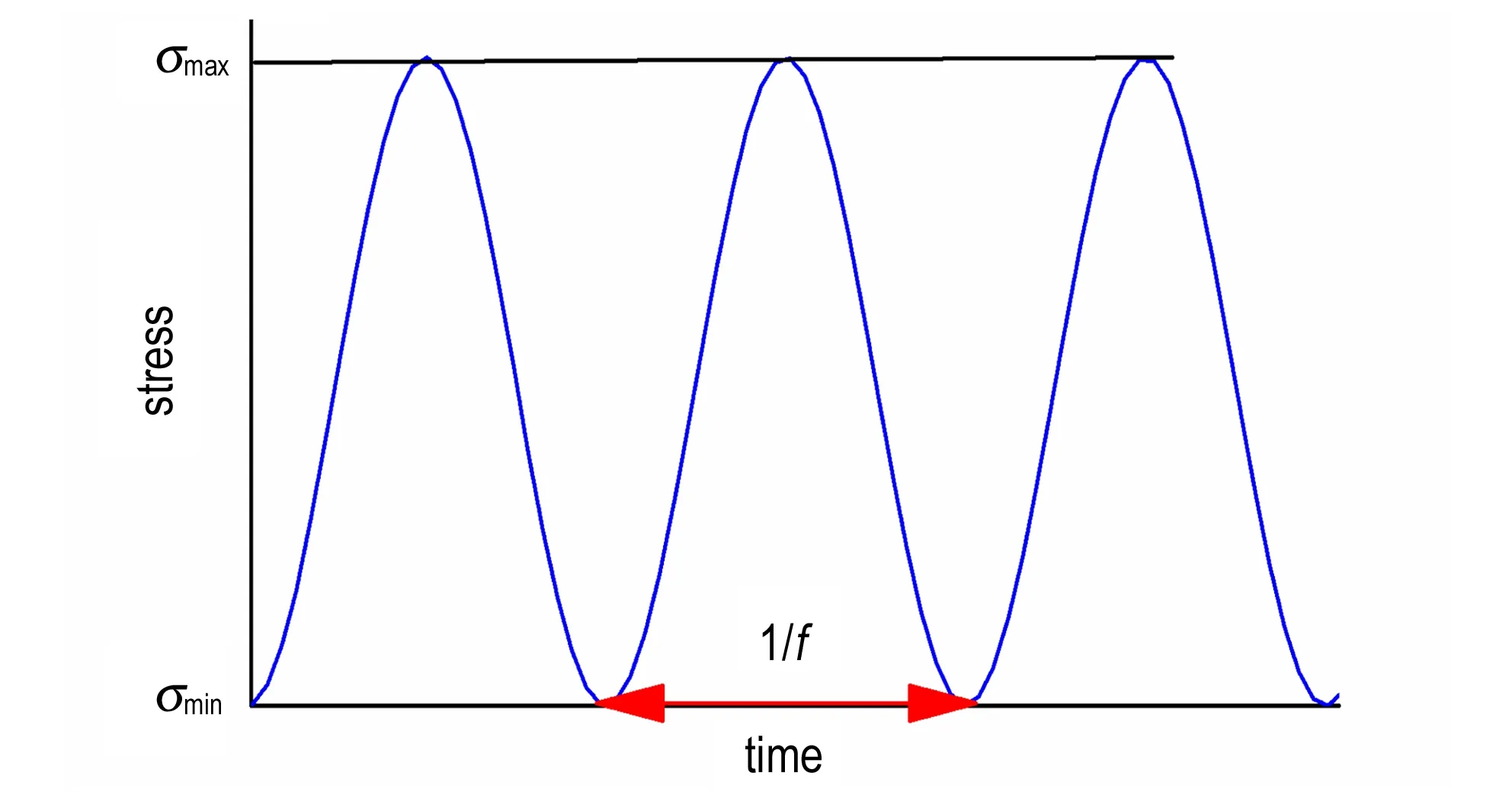
图3 疲劳试验中的应力波形

Fig.3 The waveform of stress during fatigue test

2.3 温度对疲劳寿命的影响

因为疲劳试验成本高、周期长,所以每个温度下只重复了3次,表1给出了不同温度下HTPB推进剂的疲劳试验结果。

表1 不同温度下HTPB推进剂疲劳寿命统计

Table 1 Fatigue life statistics of HTPB propellant at different temperatures

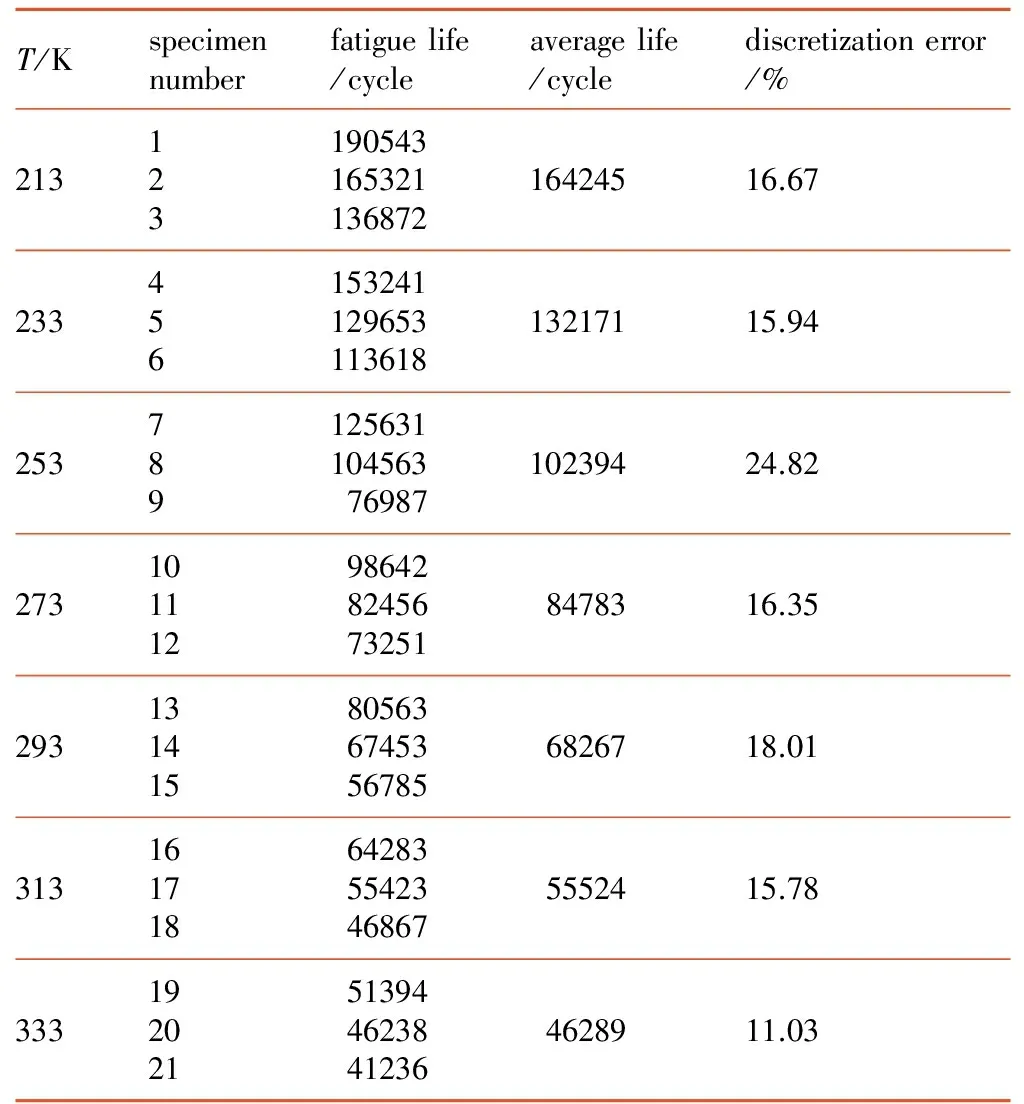
T/Kspecimennumberfatiguelife/cycleaveragelife/cyclediscretizationerror/%21312319054316532113687216424516．6723345615324112965311361813217115．942537891256311045637698710239424．822731011129864282456732518478316．352931314158056367453567856826718．013131617186428355423468675552415．783331920215139446238412364628911．03

从表1可看出,同一温度下的疲劳寿命有一定的散差,最大达到了24.82%,最小的也有11.03%,主要是由于HTPB推进剂属于颗粒复合型材料,制造过程中燃料混合不均,造成固体颗粒分布不均匀,导致药柱力学性能散差大,这也是推进剂工艺不成熟的表现。

总的来看,疲劳寿命随着温度的升高而逐渐缩短,将不同温度下的平均寿命与温度的关系进行拟合,发现满足指数型关系,拟合结果如(1)式,相关系数R2为0.982。

(1)

式中,N是材料的疲劳寿命,次;T是试验的温度,K。原因是在较高温度下,HTPB推进剂的基体材料分子运动加剧,粘性表现更加明显,在相同的应力加载下,基体与颗粒之间的脱湿加剧,从而使得疲劳寿命缩短。

2.4 温度对疲劳变形的影响

由于HTPB推进剂是粘弹性材料,当承受周期性变化的正弦应力时,材料会产生周期性的正弦应变,但是应变落后于应力,应力与应变之间有相位差,称为滞后角[15]。每个温度下滞回曲线随循环加载次数的变化趋势是相同的,本研究以313 K的应力-应变滞回曲线为例进行说明,如图4。

图4 应力-应变滞回曲线(313 K)

Fig.4 Stress-strain hysteretic curves (313 K)

由图4可见,随着循环次数的增加,滞回曲线逐渐右移,表明峰值点和谷点的应变都在不断增加。谷点(应力为0)时,应变不能完全恢复,一般将这种应变定义为残余应变,这说明材料由于粘弹性效应在疲劳加载过程中发生了明显的蠕变现象[16]。同时发现滞回曲线的形状由规整的椭圆形逐渐向弯曲不规则的扁状形变化(在疲劳断裂前的几百次循环中尤其明显),且滞回曲线的面积随着循环周次的增加而增大,这说明材料的损伤发展逐渐增强。

为了体现温度对滞回曲线的影响,选取了相同加载次数(103次)不同温度的滞回曲线,如图5所示。可以看出在相同循环加载次数下,温度越高,滞回曲线越向右移,即残余应变和峰值应变越大。同时滞回曲线面积和宽度也变大,材料粘性更加显著,这与温度升高疲劳寿命缩短的原理是相一致的。

图5 不同温度相同加载次数的滞回曲线

Fig.5 Hysteretic curves with same loading times at different temperatures

图6为不同温度下整个疲劳寿命加载周期内峰值应变演化规律图。可以看出温度越高,在相同循环次数下疲劳变形越大,达到疲劳断裂所需的循环次数越少,疲劳断裂的应变越大。并且随着循环加载次数的增加,温度对峰值应变的影响显著增加。

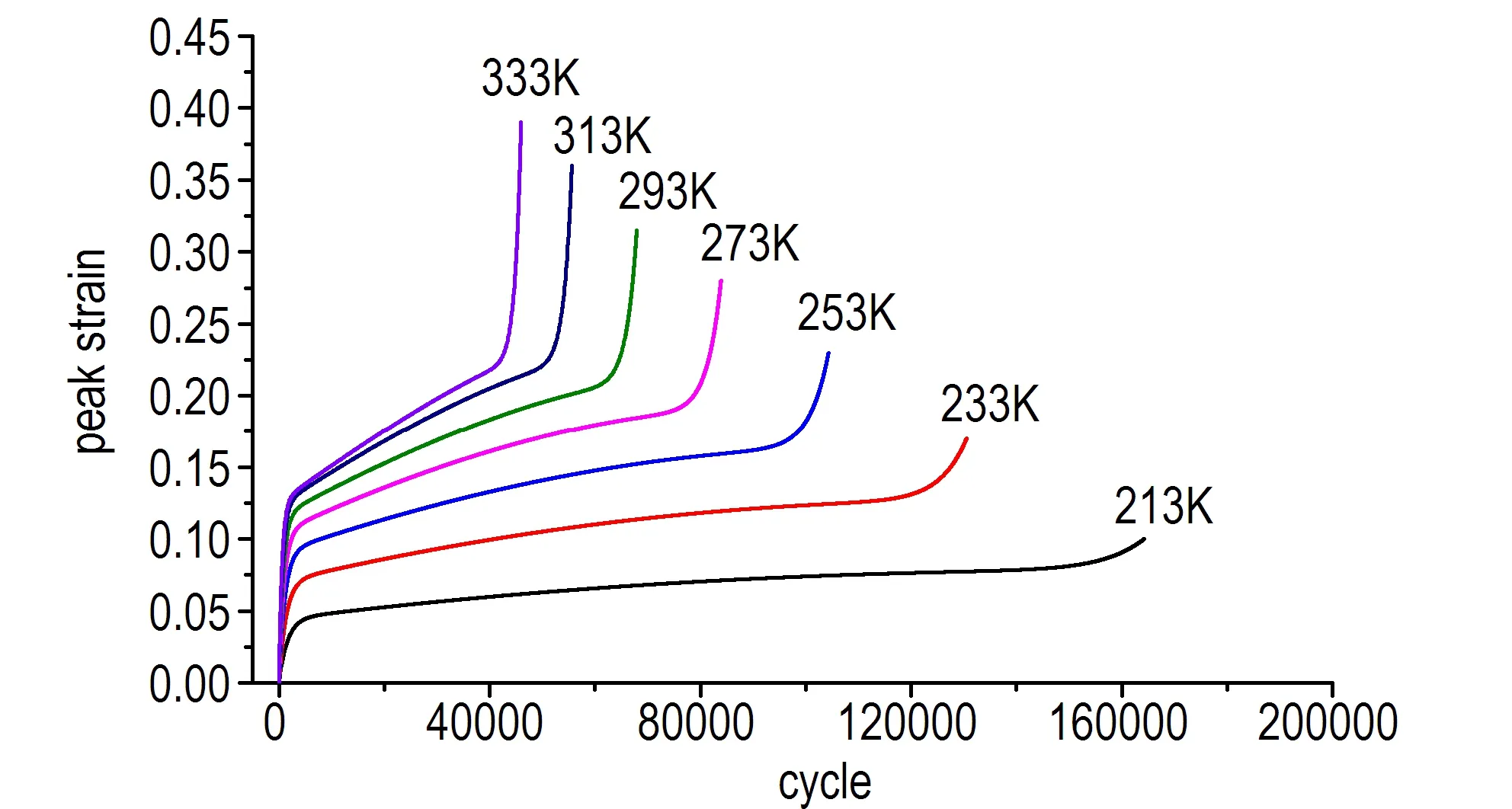
图6 不同温度的峰值应变演化规律

Fig.6 The evolution rule of peak strain at different temperatures

峰值应变随着循环次数的增加呈现出明显的三阶段发展规律: 初始变形阶段、稳定发展阶段和加速阶段。初始阶段,变形增长较快,峰值应变曲线呈现明显上凸状,该阶段持续时间较短,初始阶段变形速率随着循环次数的增加而迅速降低。直到稳定发展阶段,峰值应变演化为一条低斜率直线段,该阶段持续的时间较长。与第一阶段相比,应变增长速率大幅降低,每个循环周期产生的变形积累量很小。加速阶段曲线上凹,峰值应变高速增长直至试样疲劳断裂。所以峰值应变可以看作材料内部疲劳损伤发展的宏观表现。疲劳过程实质就是损伤不断累积,力学性能不断劣化的过程,下节将对不同温度下疲劳损伤演化规律进行研究。

3 疲劳损伤演化模型

3.1 损伤因子的选取

按照损伤演化规律的不同,疲劳损伤模型有线性损伤演化和非线性损伤演化之分。线性损伤演化是损伤与载荷重复作用次数呈线性关系,否则称为非线性损伤演化。疲劳损伤问题中的损伤往往表示成载荷循环次数的函数[17]。目前基于宏观力学性能劣化的剩余强度和剩余刚度模型[18]应用的较为广泛。本文考虑到峰值应变是材料内部损伤的宏观表现,最终选择疲劳过程的峰值应变作为损伤因子。

为了保证损伤因子D从0增加到1(0≤D≤1,其中D=0时材料无疲劳损伤,D=1时材料疲劳破坏),采取(2)式定义损伤因子:

(2)

式中,εn是材料循环加载n次时的峰值应变,εN是材料疲劳破坏时对应循环周期的峰值应变。

从图7中可以看出疲劳损伤呈现三阶段的发展规律: 损伤迅速发展、损伤发展速率较低、损伤加速发展。并且温度越高,相同寿命比下疲劳损伤值越低,第一、二两个阶段占总损伤的比例下降,第三阶段占总损伤的比例增加。

图7 不同温度下HTPB推进剂的疲劳损伤曲线

Fig.7 Fatigue damage curves of HTPB propellants at different temperatures

3.2 损伤模型的建立

目前,对第一、二阶段的损伤演化有较多的描述,如Chaboche模型,Lemaitre模型等[19]。第一阶段为循环应变松弛(蠕变)阶段,发生在循环初期,可以运用Kelvin模型的蠕变方程[20]给出如下表达式:

(3)

式中,X(t)为瞬时应力,MPa;X0为初始应力,MPa;t为时间,s;λ为延迟时间,s。

相应的损伤演化方程为:

D1(n)=Dc[1-exp(-μn/N)]

(4)

式中,Dc为第一阶段的饱和损伤量,μ为拟合常数。

第二阶段为损伤实质发展的阶段,可以通过耗散势函数来推导,本文采用一种常用的损伤演化模型[21]为:

(5)

式中,q为材料参数,对式(5)进行积分,边界条件:

D|n=0=0,D|n=N=Da得到第二阶段损伤演化方程:

D2(n)=Da[1-(1-n/N)β]

(6)

式中,Da为第二阶段的饱和损伤量,β=1/(1+q)为拟合常数。

两阶段疲劳损伤模型反映的是材料内部微孔洞和微裂纹的形成,是材料内部整体能量耗散的情况,并不能表征宏观裂纹形成后,局部应力应变严重集中情况下的疲劳损伤过程。 对于宏观裂纹形成之后,参考文献[22]认为损伤演化函数的关系为幂函数表达式:

(7)

式中,m为材料参数；A为材料疲劳抗力的系数；B为常数，与每一循环的变形量有关。

对式(7)积分,边界条件:D|n=0=0,D|n=N=Di可得:

D3(n)=Di(n/N)γ

(8)

式中,Di为第三阶段的饱和损伤量,γ=m+1为拟合常数。

通过以上推导分析,可以得到疲劳损伤三个阶段的疲劳损伤演化过程:

D=D1(n)+D2(n)+D3(n)=Dc[1-exp(-μn/N)]+

Da[1-(1-n/N)β]+Di(n/N)γ

(9)

为了更直观地看出疲劳损伤的发展过程,以313 K为例,将损伤演化过程分解为三个阶段,如图8所示。

由图8可知,第一阶段的循环应变松弛只占整个疲劳寿命的很小一部分,并很快达到饱和,达到饱和后这部分的损伤不再发展; 第二阶段是微孔洞和微裂纹的萌生和扩展,贯穿整个循环过程并且趋于某一个饱和状态,这个阶段占疲劳寿命的绝大部分; 宏观裂纹是在循环加载后期,当微裂纹和微孔洞增加到一定值时产生的,宏观裂纹产生后,损伤迅速增加直至材料失效。并且三个阶段的饱和损伤值相加为1,即Dc+Da+Di=1。

图8 疲劳损伤演化模型三阶段的分离

Fig.8 Three-stage separation of fatigue damage evolution model

3.3 模型参数的获取和验证

试验所得的HTPB推进剂的疲劳试验数据统计分析结果见表2。从表2中可以看出Dc,μ,Da,β随着温度的升高而逐渐减小,Di,γ随着温度的升高而逐渐增加,相关系数都达到了99%以上。

表2 疲劳试验与模型参数统计结果

Table 2 Fatigue test and model parameter statistical results

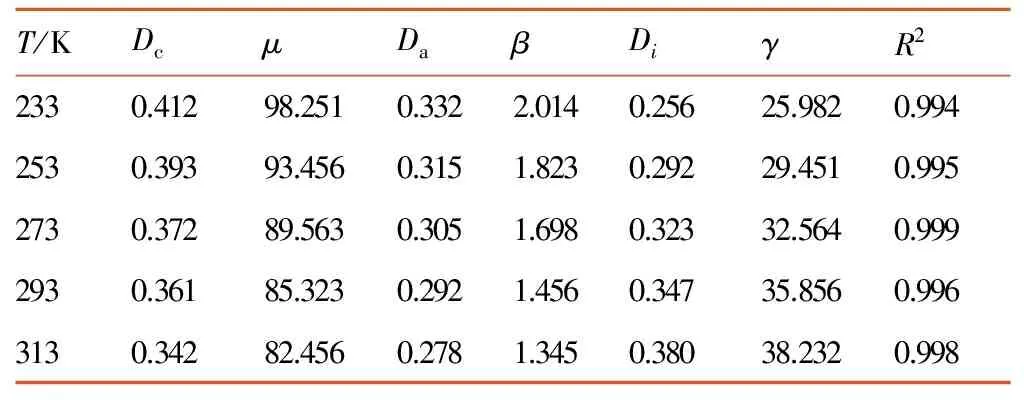
T/KDcμDaβDiγR22330．41298．2510．3322．0140．25625．9820．9942530．39393．4560．3151．8230．29229．4510．9952730．37289．5630．3051．6980．32332．5640．9992930．36185．3230．2921．4560．34735．8560．9963130．34282．4560．2781．3450．38038．2320．998

Note:Dcis the saturation damage of the first stage;Dais the saturation damage of the second stage;Diis the saturation damage of the third stage;μ,β,γare fitting constants.

将表中的模型参数进行拟合,发现其与温度的关系符合线性关系,相关系数都大于97%。

拟合的结果为:

(10)

将式(10)代入到式(9)中即可得到频率为20 Hz,控制应力为0.4 MPa的HTPB推进剂的不同温度的疲劳损伤演化方程。

图9为采用本文所构建的疲劳损伤模型理论结果与图7中T=213 K和333 K的试验结果对比。可以看出,在循环初期理论结果与试验结果吻合很好,随着加载次数的增加,出现了一定的误差,误差产生的原因主要是加载周期微裂纹的扩展和脱湿点的张开闭合比较复杂[23],其次试验本身也存在一定的误差,总的来说试验和理论结果吻合度比较好。

图9 理论和试验结果比较

Fig.9 Comparison of the theoretical results and experimental ones

4 结 论

(1) 同一温度下HTPB推进剂的疲劳寿命具有一定的散差,但总的来看,温度从213 K升高到333 K,疲劳平均寿命从164245次缩短到46289次,主要因为温度升高,材料的粘性增强,基体与颗粒之间的脱湿加剧,从而使得疲劳寿命缩短。

(2) 疲劳载荷作用下,峰值应变首先经历初始变形阶段,然后进入稳定发展阶段,最后应变快速增长直至疲劳失效。并且温度越高,相同循环次数下的疲劳变形越大,达到疲劳断裂所需的循环次数越少,疲劳断裂应变越大。

(3) HTPB推进剂损伤过程主要包括循环应变松弛、微孔洞和微裂纹的萌生和发展、宏观裂纹的萌生和扩展三个阶段。本文建立了考虑宏观裂纹发展的含温度效应的损伤模型,可以很好地表征频率为20 Hz,控制应力为0.4 MPa的HTPB推进剂213～333 K温度范围内的损伤演化规律。

参考文献:

[1] 周红梅, 王连生, 王宏伟, 等. 随机载荷下固体发动机药柱粘弹动力响应[J]. 导弹与航天运载技术, 2009(5): 46-49.

ZHOU Hong-mei, WANG Lian-sheng, WANG Hong-wei, et al. Viscous-elastic dynamic response for SRM grain under random loading[J].MissileandSpaceVehicle, 2009(5): 46-49.

[2] Lin Y K, Yang J N. A stochastic theory of fatigue crack propagation[J].AiaaJournal, 2015, 23(23): 117-124.

[4] Drozdov A D. Cyclic thermo-viscoplasticity of high density polyethylene[J].InternationalJournalofSolids&Structures, 2010, 47(11): 1592-1602.

[5] Jurbergs N, Long A, Ticona L, et al. Cyclic behavior of short glass fiber reinforced polyamide for fatigue life prediction of automotive components[J].ProcediaEngineering, 2010, 2(1): 901-910.

[6] Paepegem W V, Degrieck J. A new coupled approach of residual stiffness and strength for fatigue of fibre-reinforced composites[J].InternationalJournalofFatigue, 2002, 24(7): 747-762.

[7] 高艳宾, 许进升, 陈雄, 等. 应变控制下NEPE推进剂非线性疲劳损伤[J]. 航空动力学报, 2015, 30(6): 1486-1491.

GAO Yan-bin, XU Jin-sheng, CHEN Xiong, et al. Nonlinear fatigue damage of nitrate ester plasticized polyether propellant for strain-control[J].JournalofAerospacePower, 2015, 30(6): 1486-1491.

[8] 李金飞, 黄卫东, 李高春, 等. 振动载荷对定应变HTPB推进剂力学性能影响[J]. 推进技术, 2016, 37(2): 372-377.

LI Jin-fei, HUANG Wei-dong, LI Gao-chun, et al. Effects of vibration load on mechanical properties of HTPB propellant with constant strain[J].JournalofPropulsionTechnology, 2016, 37(2): 372-377.

[9] Lee K O, Hong S G, Lee S B. A new energy-based fatigue damage parameter in life prediction of high-temperature structural materials[J].MaterialsScience&EngineeringA, 2008, 496(1-2): 471-477.

[10] 刘著卿, 李高春, 王玉峰, 等. 应变加载历史对推进剂力学性能的影响[J]. 火炸药学报, 2010, 33(4): 5-9.

LIU Zhu-qing, LI Gao-chun, WANG Yu-feng, et al. Effect of strain loading history on the mechanical property of propellant[J].ChineseJournalofExplosives&Propellants, 2010, 33(4): 5-9.

[11] 王玉峰, 李高春, 刘著卿, 等. 应变率和加载方式对HTPB推进剂力学性能及耗散特性的影响[J]. 含能材料, 2010, 18(4): 377-382.

WANG Yu-feng, LI Gao-chun, LIU Zhu-qing, et al. Effect of strain rate and loading on mechanical properties and dissipated energy for HTPB propellant[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2010, 18(4): 377-382.

[12] 王海波, 王永安, 钟峰. 交变温度作用下推进剂耗散能与累计损伤的数值计算[J]. 舰船电子工程, 2014(11): 90-93.

WANGHai-bo, WANG Yong-an, ZHONG Feng. Calculation of dissipated energy and accumulated damage of propellant under alternating temperature loads[J].ShipElectronicEngineering, 2014(11): 90-93.

[13] 曲凯, 邢耀国, 张旭东. 摇摆载荷作用下舰载固体火箭发动机药柱疲劳损伤[J]. 航空动力学报, 2011, 26(11): 2636-2640.

QU Kai, XING Yao-guo, ZHANG Xu-dong. Fatigue damage of shipborne solid rocket motor propellant under swing loading[J].JournalofAerospacePower, 2011, 26(11): 2636-2640.

[14] 邓斌, 董可海, 谢燕. 基于能量耗散的药柱粘弹性累积损伤[J]. 国防科技大学学报, 2013, 35(1): 24-27.

DENG Bin, DONG Ke-hai, XIE Yan. Viscoelastic cumulative damage of solid propellant grain based on energy dissipation[J].JournalofNationalUniversityofDefenseTechnology, 2013, 35(1): 24-27.

[15] Mivehchi H, Varvani-Farahani A. The effect of temperature on fatigue strength and cumulative fatigue damage of FRP composites[J].ProcediaEngineering, 2010, 2(1): 2011-2020.

[16] 赵欣欣, 王正道. 聚酰亚胺无机杂化薄膜疲劳性能研究[J]. 工程力学, 2008, 25(5): 67-72.

ZHAO Xin-xin, WANG Zheng-dao. Evaluation of the fatigue performance of pi-inorganic hybrid films[J].EngineeringMechanics, 2008, 25(5): 67-72.

[17] Liu R, Zhang Z J, Zhang P, et al. Extremely-low-cycle fatigue behaviors of Cu and Cu-Al alloys: damage mechanisms and life prediction[J].ActaMaterialia, 2015, 83: 341-356.

[18] Dattoma V, Giancane S, Nobile R, et al. Fatigue life prediction under variable loading based on a new non-linear continuum damage mechanics model[J].InternationalJournalofFatigue, 2006, 28(2): 89-95.

[19] Lemaitre J A, Plumtree A. Application of Damage Concepts to Predict Creep-Fatigue Failures[J].JournalofEngineeringMaterials&Technology, 1979, 101(3): 284-292.

[20] 程光旭, 韦玮. 复合材料疲劳损伤演化的两阶段模型[J]. 机械工程材料, 2000, 24(5): 1-4.

CHENG Guang-xu, WEI Wei. A general two stage model for accumulation of fatigue damage in composite materials[J].MaterialsforMechanicalEngineering, 2000, 24(5): 1-4.

[21] Wang Y, Ma L, Fan P, et al. A fatigue damage model for rock salt considering the effects of loading frequency and amplitude[J].InternationalJournalofMiningScienceandTechnology, 2016, 26(5): 955-958.

[22] 吴健栋, 蔡志鹏, 汤之南, 等. 低周疲劳过程损伤变量的复合分析法和三阶段损伤演化模型[J]. 机械工程学报, 2015, 51(10): 86-95.

WU Jian-dong, CAI Zhi-peng, TANG Zhi-nan, et al. Combination analyzing method to characterize damage variable and three stage model of fatigue damage in low-cycle fatigue[J].JournalofMechanicalEngineering, 2015, 51(10): 86-95.

[23] 常武军, 鞠玉涛, 王蓬勃. HTPB推进剂脱湿与力学性能的相关性研究[J]. 兵工学报, 2012, 32(3): 261-266.

CHANG Wu-jun, JU Yu-tao, WANG Peng-bo. Research on correlation between dewetting and mechanical property of HTPB propellant[J].ActaArmamentarii, 2012, 32(3): 261-266.