一种RDX基温压炸药的JWL-Miller状态方程研究

田少康, 李 席, 刘 波, 范 伟, 韩志伟, 王伯良

(1. 南京理工大学化工学院, 江苏 南京 210094; 2. 山西淮海机电有限公司, 山西 长治 046012)

1 引 言

温压炸药(Thermobaric Explosive,简称TBE)是一类含有高能金属粉(如Al) 的混合炸药,一般还添加助燃剂(如高氯酸铵)使其在高能炸药爆炸后快速反应以提供后期铝粉燃烧需要的高温条件,因而与普通含铝炸药反应过程有明显的不同[1],是一种典型的非理想炸药[2]。

JWL(Jones-Wilkins-Lee)状态方程是一种能反映炸药做功能力[3]的半经验状态方程,可以精确地描述爆炸加速金属过程中爆轰产物的压力-体积-能量特性[4],已被广泛应用于炸药爆轰产物的描述。JWL状态方程的参数一般由圆筒试验[5]确定。陈朗等[6]对某含铝炸药进行了Ф50 mm的圆筒试验,通过圆筒试验的二维数值模拟,标定了含铝炸药的状态方程参数; 计冬奎等[7]利用Ф25 mm和Ф50 mm圆筒试验共同确定了含铝炸药JWL 状态方程,并得到了尺寸效应与做功能力的关系。韩勇等[8]通过圆筒试验研究了不同尺寸含铝炸药的做功能力,探讨了含铝炸药二次反应的问题,提出在对含铝炸药的圆筒实验进行数值模拟时 ,必须考虑含铝炸药的反应速率方程; 裴红波[9]等研究认为RDX基含铝炸药中铝粉的完全反应时间为50～200 μs,而圆筒试验破片加速过程中铝粉后燃能量尚未完全释放。因此,仅靠圆筒试验确定的JWL状态方程不能完整描述含铝非理想炸药爆轰产物的状态,难以满足温压炸药威力评价及数值模拟的需要。

A.L.Kuhl等[10-11]采用两相燃烧模型对含铝炸药的爆炸和后燃效应进行了模拟研究。Miller等[12]通过试验得到了含铝炸药中铝粉的反应速率方程,得到了带有二次反应的JWL 状态方程,且与试验结果吻合较好。辛春亮等[13]提出可以通过试验结果反推出Miller反应速率方程参数。温压炸药中铝粉含量较高,铝粉二次反应能量的释放不可忽略。而目前国内在对于温压炸药状态方程的研究过程中,很少考虑非理想成分铝粉的能量释放,这难以对其爆炸能量释放过程进行全面地描述。因此,研究确立带有二次反应的JWL状态方程对温压炸药爆轰性能的研究和应用具有重要的意义。基于此,本研究对RDX基温压炸药(RDX/Al/其它=53/35/12)进行了Ф25 mm圆筒试验,获得了圆筒壁膨胀位移、速度与时间的关系,利用ANSYS/LS-DYNA有限元软件数值模拟,确定了其爆轰产物的JWL状态方程参数,在此基础上,通过野外静爆试验与数值模拟相结合,最终得到了带有二次反应速率的温压炸药状态方程参数,为温压炸药爆轰产物状态方程的更深入研究提供参考。

2 JWL状态方程参数的确定

2.1 圆筒试验

试验按照GJB772A-1997方法705.2[14]进行,采用Ф25 mm的圆筒试验,待测炸药为RDX基温压炸药, 采用压装成型工艺,平均装药密度为1.966 g·cm-1; 圆筒材料为1号无氧铜,尺寸为Ф25 mm×300 mm(壁厚2.5 mm); 试验装置由高压电雷管、传爆药柱、电探针、圆筒管和爆炸光源等组成,固定于两端的电探针与时间记录仪器相连接,用来测量炸药爆速,试验装置见图1[14]。高速摄像拍摄位置距起爆端200 mm,转速7.5×103r·min-1,管壁膨胀扫描图像见图2。

图1 圆筒试验装置图

1,7—电雷管, 2,6—传爆药柱, 3—圆筒, 4—高速相机, 5—光源弹, 8—参试药柱, 9—电探针

Fig.1 Cylinder test setup

1,7—electric detonator, 2,6—booster, 3—cylinder, 4—high-speed camera, 5—lamp-house bomb, 8—sample, 9—electric probe

图2 铜管膨胀扫描图像

Fig.2 Photograph of the copper cylinder expansion process

2.2 试验结果

从一侧起爆装填在圆筒内的温压炸药后,圆筒壁会在爆轰产物作用下沿圆筒的径向和轴向做二维运动,膨胀距离(R-R0)与膨胀时间t的关系如下式:

t=A+B(R-R0)+CeD(R-R0)

(1)

式中,R-R0为圆筒壁膨胀距离,mm;t为圆筒壁膨胀到某距离对应的时间,μs;A、B、C、D为拟合系数。根据最小二乘法原理[14],对试验得到的膨胀时间t与膨胀距离(R-R0)进行拟合,得到系数A=3.2630,B=0.6590,C=-2.4012,D=-0.12803。

利用得到的A、B、C、D值,圆筒壁膨胀到某一距离(R-R0)的壁速u及比动能E,可分别由(2)、(3)式计算:

(2)

(3)

对于Ф25 mm的圆筒试验,选取膨胀距离为6 mm和19 mm时的u和E来表征炸药的做功能力,试验结果见表1。

表1 圆筒试验结果

Table 1 Cylinder test results

R-R0/mmt/μsu/mm·μs-1E/kJ·g-166．101．240±0．0080．768±0．0101915．571．457±0．0011．061±0．002

2.3 圆筒试验数值模拟

采用有限元动力学程序ANSYS/LS -DYNA[15]对圆筒试验结果进行数值模拟,建立Lagrange坐标(R,Z,t),即质量的原始坐标为(R,Z),计算中跟踪质量。按照试验中的实际尺寸,建立1/4对称的3D模型,网格单元采用六面体SOLID164单元,几何模型如图3所示。

图3 圆筒试验的几何模型

Fig.3 Cylinder test model

材料模型: 紫铜管壁材料采用John-cook材料模型[16],Gruneisen状态方程[17-18],其形式为:

(4)

式中,C1是μs-μp(冲击波速度-质点速度)曲线的截距,S1,S2,S3是μs-μp曲线斜率系数,a是Gruneisen系数的一阶体积修正,γ0是Gruneisen系数,E为材料内能。模拟中紫铜的参数由文献[16]获得,具体数据见表2。

表2 紫铜的Gruneisen状态方程参数

Table 2 The parameters of Gruneisen equation of state of copper

C1/mm·μs-1S1S2S3γ0a3．941．489001．990

对于待测温压炸药,采用HIGH-EXPLOSIVE-BURN材料模型和JWL状态方程,其形式为:

p=A[1-ω/(R1v)]e-R1v+

B[1-ω/(R2v)]e-R2v+ωE/v

(5)

在等熵条件下,JWL状态方程形式为:

ps=Ae-R1v+Be-R2v+C/vω+1

(6)

(7)

(8)

(9)

对于大多数炸药来说,R1、R2和ω值的选取范围是R1=4～5、R2=1～2、ω=0.2～0.4。因此,在开始模拟计算时,先代入一组已知的与待测温压炸药组分相近炸药的R1、R2和ω值[8],通过三个关系式计算得到相应的A、B和C值; 将得到的一组参数带入LS-DYNA进行模拟计算,得到圆筒膨胀距离与时间的关系曲线,把它与实验测得的圆筒膨胀距离时间曲线相比较,根据它们之间的差别,调整参数值后进行下一次计算。这样经过多次反复计算,不断修正状态方程参数,直到计算膨胀距离时间曲线与试验曲线间的误差小于1%时,所使用状态方程参数为所要标定的参数。

按照上述方法,最终得到圆筒膨胀距离R-R0与膨胀时间t以及膨胀速度u之间关系分别如图4所示,圆筒膨胀过程中的计算值和试验值的相对误差已小于1%。得到所测温压炸药爆轰产物的JWL状态方程参数见表3。

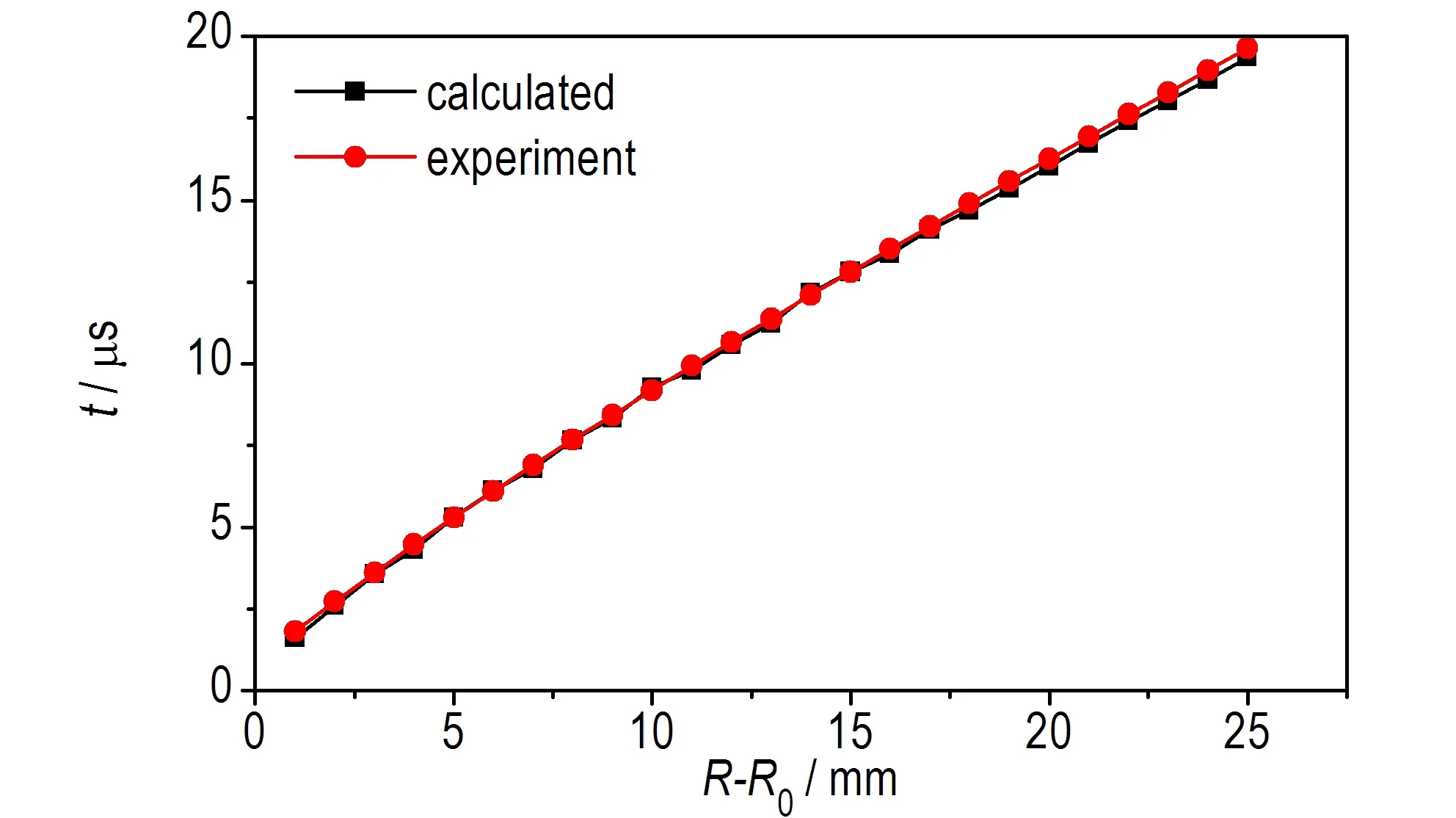
a. (R-R0)-t

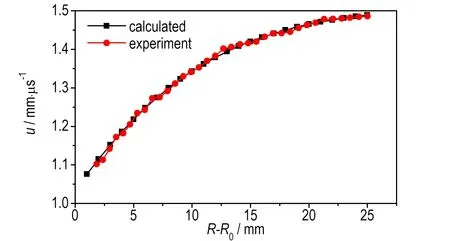
b. (R-R0)-u

图4 温压炸药圆筒试验中圆筒膨胀过程的计算值与测试结果

Fig.4 Calculated and tested expansion velocity and expansion distance curves in cylinder test of TBE

表3 温压炸药爆轰产物JWL状态方程参数

Table 3 The parameters of the JWL equation of state of the detonation product of TBE

ρ0/g·cm-3D/m·s-1pCJ/GPaE0/J·g-1A/GPaB/GPaC/GPaR1R2ω1．966768227．57058752．118．51．534．471．730．38

3 二次反应速率方程参数确定

3.1 温压炸药野外静爆试验

对被测温压炸药进行野外静爆试验。试验场地选择在空旷的野外,地面平坦,硬度适中。爆心距地面1 m,温压药柱药量750 g,直径8 cm,高7.6 cm。均以钝化黑索金作为传爆药,用8号电雷管上端起爆。试验采用压电式压力传感器获取冲击波参数,以药柱在地面上的垂直投影点为圆心,测点分布在半径为3,4,5,7 m的圆周上,传感器分布情况如图5所示。试验所得3 m处冲击波超压曲线如图6所示,其中Δp为冲击波超压峰值,t+为正压作用时间,i+为正压冲量。

图5 传感器分布图

Fig.5 Sensor arrangement chart

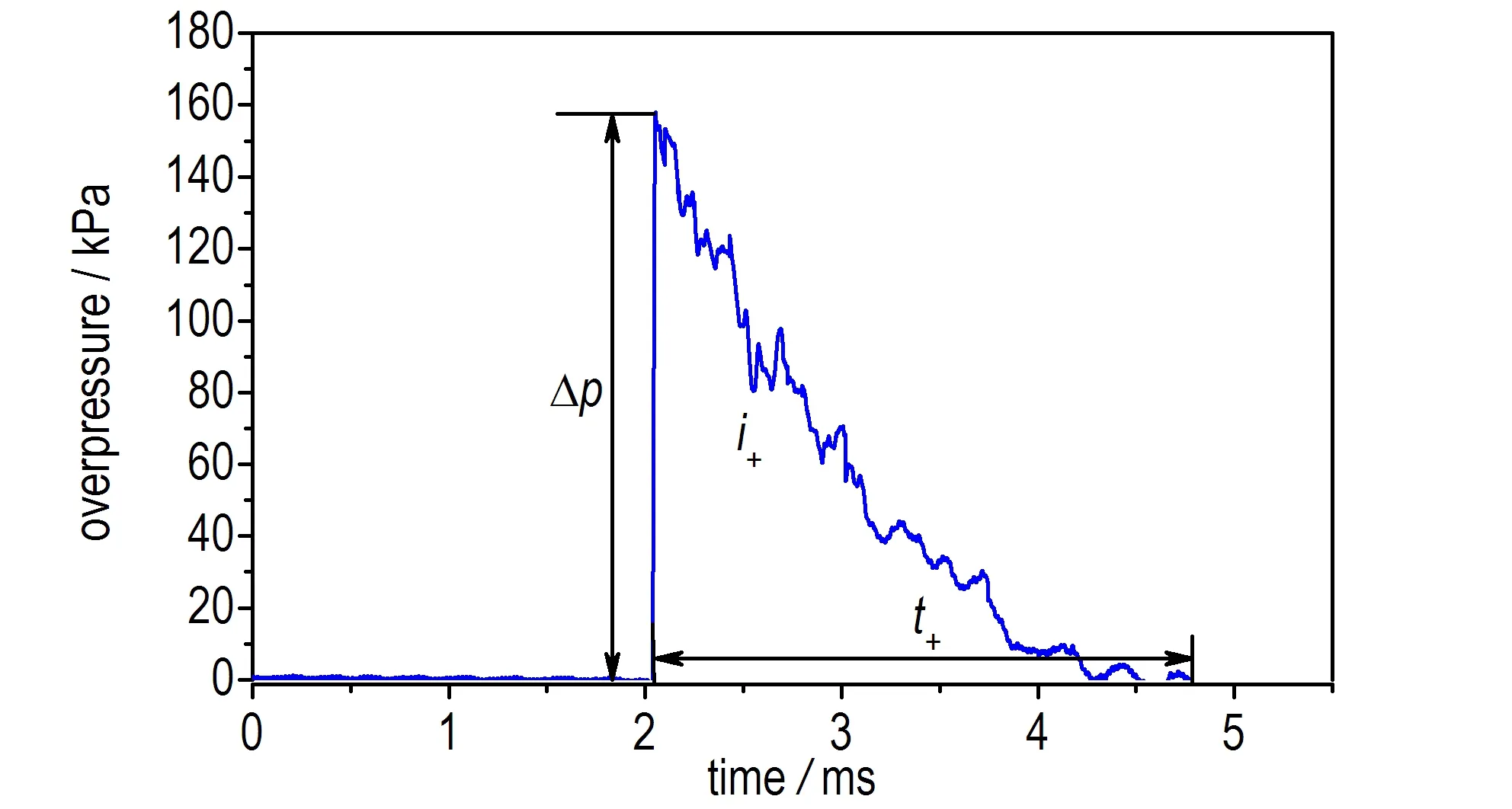
图6 试验所得温压炸药冲击波波形

Fig.6 Shock waves history of TBE measured by the experiment

3.2 二次反应速率方程参数

将2.3中得到的JWL方程参数带入ANSYS/AUTODYN有限元分析软件,对静爆试验进行模拟,建立模型如图7所示,采用轴对称结构,装药量、炸高以及装药尺寸均与试验一致; 空气域网格尺寸为5 mm,炸药域网格尺寸为2 mm,AB线段为对称轴,设置线段BC、CD设置为流出边界,AD线段为刚性地面,在其3,4,5,7 m处添加监测点。

模型中空气域采用理想气体模型,采用AUTODYN默认参数; 爆轰产物状态方程选用带有二次反应的JWL-Miller模型状态方程[13],其形式为:

(10)

从方程(10)中可以看出,与JWL方程相比,JWL-Miller模型方程保持了JWL方程参数不变,额外增加了非理想成分(如铝粉)的能量释放参数λQ,唯象地描述温压炸药中铝粉的二次反应对冲击波能量的补充; 其中,Q为非理想成分含有的热量,kJ·m-3;λ为非理想成分的反应度。其能量释放速率可用(11)式来表述:

(11)

式中,a为能量释放常数;m为能量释放指数;n为压力指数,这些参数与铝粉在后燃中的特性有关。

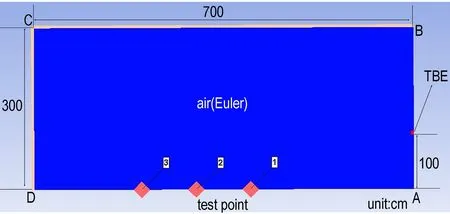
图7 2-D模型

Fig.7 2-D model

在文献[20]的基础上,通过调整a,m,n的值改变铝粉的二次反应速率,模拟爆炸场中的压力变化情况。将超压模拟值与试验值进行比较,根据差别再次调整参数,直到模拟结果与试验结果吻合较好。图8为最终得到的各距离处的压力曲线图; 表4中列出了不同距离处的冲击波超压峰值Δp和冲量i+的试验值和模拟计算值以及二者之间的相对误差ε。

温压炸药的冲击波效应主要以超压峰值与正压冲量为评判依据。与试验值相比,除5 m处的正压冲量的相对误差为7.9%外,其余测点的超压峰值与正压冲量的相对误差小于±5%。根据此结果确定了温压炸药JWL-Miller模型中铝粉二次反应速率方程的参数,a=0.14,m=0.61,n=0.15。

JWL-Miller能量释放模型中充分考虑了温压炸药中铝粉二次反应对能量释放的影响。由图8和表4中可以看出,相比于JWL方程,Miller模型的加入对于超压峰值和正压冲量都有较大提高,平均提高达25%,这也与阚金玲等[19]的研究结果相符,说明了本研究得出参数的有效性,也表明该JWL-Miller模型参数在实际静爆试验的研究计算中可以较为准确地反映爆炸场压力变化情况。

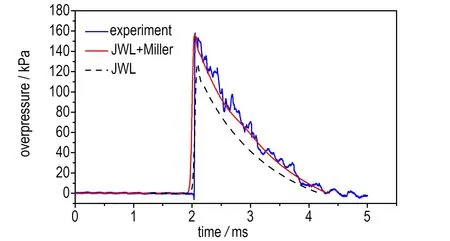
a. 3 m

c. 5 m

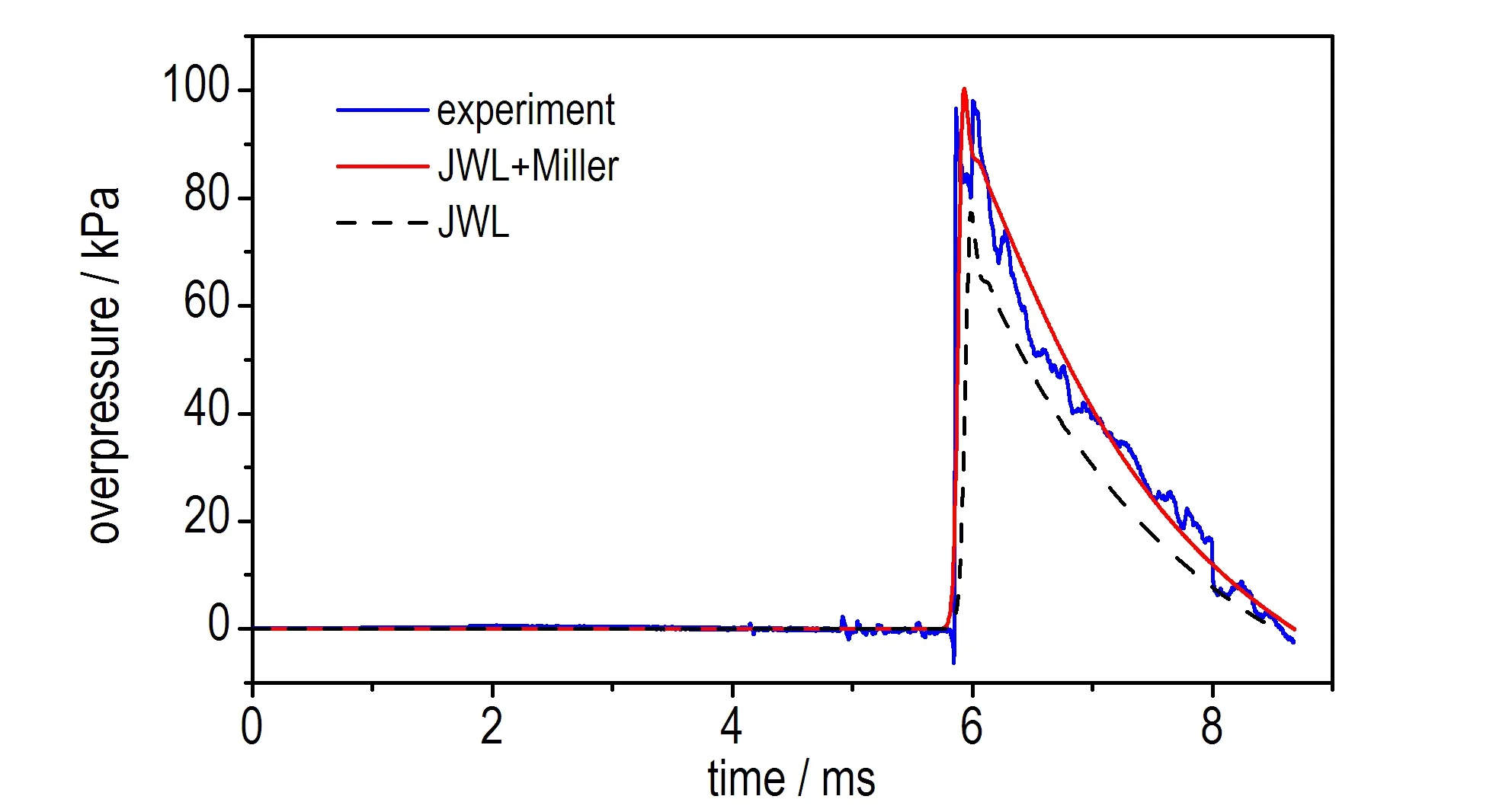
b. 4 m

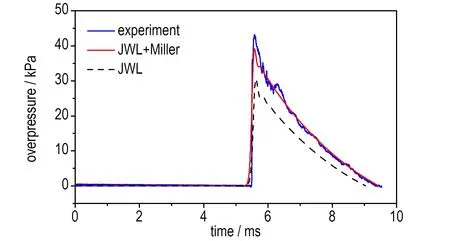
d. 7 m

图8 试验和模拟所得的冲击波波形对比

Fig.8 Comparison between pressure-time curves of numerical simulation and that of testing

表4 试验和模拟所得冲击波参数对比

Table 4 Blast waves parameters comparison of simulation results and experiment data

d/m3Δp/kPai+/Pa·s4Δp/kPai+/Pa·s5Δp/kPai+/Pa·s7Δp/kPai+/Pa·sexperiment157．6132．595．5102．169．778．942．462．1JWL⁃Millercalculated156．7131．596．5103．267．785．740．161．8εi/%-0．6-0．81．01．1-3．17．9-5．00．5JWLcalculated125．694．276．573．152．459．130．242．9εj/%-20．3-28．9-19．9-28．4-24．8-25．1-28．7-30．9

Note: Δpis blast wave overpressure;i+is blast wave impluse;εirepresents the error between expriment and JWL-Miller calculated;εjrepresents the error between expriment and JWL calculated.

4 结 论

针对某RDX基温压炸药,通过圆筒试验确定了其爆轰产物的JWL状态方程; 并通过野外静爆试验与数值模拟相结合,获得了温压炸药中铝粉二次反应速率方程参数,得出了以下结论:

(1) 通过Ф25 mm标准圆筒试验及三维数值模拟,得到了典型温压炸药中理想成分的JWL状态方程参数:A=752.1 GPa,B=18.5 GPa,C=1.53 GPa,R1=4.47,R2=1.73,ω=0.38。

(2) 对被测温压炸药进行野外静爆试验,运用AUTODYN有限元分析软件对其结果进行模拟,确定了JWL-Miller能量释放模型中铝粉二次反应速率方程参数,a=0.14,m=0.61,n=0.15。

(3) 相比于JWL方程的计算结果,JWL-Miller模型计算所得的正压作用时间较长,正压冲量提高超过25%,体现了铝粉二次反应对冲击波的能量补充,说明JWL-Miller模型能够更为准确合理地描述温压炸药中铝粉的后燃特性。

参考文献:

[1] 黄菊, 王伯良, 仲倩, 等. 温压炸药能量输出结构的初步研究[J]. 爆炸与冲击, 2012, 32(2):164-168.

HUANG Ju, WANG Bo-liang, ZHONG Qian, et al. The preliminary investigation on energy output structure of a thermobaric explosive[J].ExplosiveandShockWaves, 2012, 32(2): 164-150.

[2] 恽寿榕, 赵衡阳. 爆炸力学[M]. 北京:国防工业出版社, 2005: 35-36.

YUN Shou-rong, ZHAO Heng-yang. Explosion mechanics[M]. Beijing: National Defense Industry Press, 2005: 35-36. (in Chinese)

[3] Lee E L, Hornig H C, Kury J W. Adiabatic expansion of high explosive detonation products, UCR-50422[R]. Livermore: California University, 1968.

[4] 张宝钅平, 张庆明, 黄风雷. 爆轰物理学[M]. 北京: 兵器工业出版社, 2006: 153.

ZHANG Bao-ping, ZHANG Qing-ming, HUANG Feng-lei. Detonation Physics[M]. Beijing: The Publishing House of Ordance Industry, 2006: 153.

[5] Kury J W. Metal acceleration by chemical explosives[C]∥4th Symp ( International) on Detonation. White Oak: Office of Naval Research, 1965: 3-12.

[6] 陈朗, 冯长根, 黄毅民. 含铝炸药圆筒试验及爆轰产物JWL状态方程研究[J]. 火炸药学报, 2001, 24(3): 13-15.

CHEN Lang, HUANG Yi-min, FENG Chang-gen. The cylinder test and JWL equation of state detonation product of aluminized explosives[J].ChineseJournalofExplosives&Propellants, 2001, 24(3): 13-15.

[7] 计冬奎, 高修柱, 肖川, 等. 含铝炸药做功能力和JWL状态方程尺寸效应研究[J]. 兵工学报, 2012, 33(5): 552-555.

JI Dong-kui, GAO Xiu-zhu, XIAO Chuan, et al. Study on dimension effect of accelerating ability and JWL equation of state for aluminized explosive[J].ActaArmamentarii, 2012, 33(5): 552-555.

[8] 韩勇, 黄辉, 黄毅民, 等. 含铝炸药圆筒试验与数值模拟[J]. 火炸药学报, 2009, 32(4): 14-17.

HAN Yong, HUANG Hui, HUANG Yi-min, et al. Cylinder test of aluminized explosives and its numerical simulation[J].ChineseJournalofExplosives&Propellants, 2009, 32(4): 14-17.

[9] 裴红波, 焦清介, 覃剑峰. 基于圆筒实验的RDX/Al炸药反应进程[J]. 爆炸与冲击, 2014, 34(5): 636-640.

PEI Hong-bo, JIAO Qing-jie, QIN Jian-feng. Reaction process of aluminized RDX-based explosive based on cylinder test[J].ExplosiveandShockWaves, 2014, 34(5): 636-640.

[10] Kuhl A L, Bell J B, Beckner V E, et al. Simulation of Aluminum Combustion and PETN Afterburning in a Confined Explosion[C]∥21st International Colloquium on the Dynamics of Explosions and Reactive Systems (ICDERS). 2007: 23-27.

[11] Kuhl A L, Bell J B, Beckner V E, et al. Numerical simulations of thermobaric explosions[J].EnergeticMaterials, 2007, 38.

[12] Miller P J, Guirguis R H. Experimental study and model calculations of metal combustion in AL/AP underwater explosives[C]∥MRS Proceedings. Cambridge University Press, 1992, 296: 299.

[13] 辛春亮, 徐更光, 刘科种, 等. 含铝炸药Miller能量释放模型的应用[J]. 含能材料, 2008, 16(4): 436-440.

XIN Chun-liang, XU Geng-guang, LIU Ke-zhong, et al. Application of Miller energy release model for aluminized explosive[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2008, 16(4) : 436-440.

[14] GJB772A-1997 方法705.2. 炸药试验方法[S]. 北京:国防科工委军标出版发行部, 1997: 290-299.

[15] ANSYS/LS-DYNA中国技术支持中心. ANSYS/LSDYNA算法基础和使用方法[M]. 北京: 北京理工大学出版社, 1999.

[16] Johnson G R, Cook W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures[C]∥Proceedings of the 7th International Symposium on Ballistics. 1983, 21: 541-547.

[17] Daniel J S. An equation of state for polymethylmethacrylate[R]. UCID-16982, 1975.

[18] Lee E, Breithaupt D, Mcmillan C, et al. The motion of thin metal walls and the equation of state of detonation products, UCID-91490[R]. Livermore-Lawrence Livermore National Laboratory, 1985.

[19] 孙承纬, 卫玉章, 周之奎. 应用爆轰物理[M]. 国防工业出版社, 2000.

[20] 周正青, 聂建新, 郭学永, 等. 一种以RDX为基含铝炸药状态方程的研究[J]. 兵工学报, 2014(增刊2): 338-342.

ZHOU Zheng-qing, NIE Jian-xin, GUO Xue-yong, et al. Studies on equation of state of detonation product for RDX-based aluminized explosive[J].ActaArmamentarii, 2014(Suppl.2): 338-342.

[21] 阚金玲, 刘家骢. 一次引爆云爆剂的爆炸特性-后燃反应对爆炸威力的影响[J]. 爆炸与冲击, 2006, 26(5): 404-409.

KAN Jin-ling, LIU Jia-cong. The blast characteristic of SEFAE effect of after burning on blast power[J].ExplosionandShockWaves, 2006, 26(5): 404-409.