基于改进粒子群优化极限学习机的养殖氨态氮含量预测模型
徐大明+杜永贵+孙传恒 周超
摘要:针对养殖水体氨态氮含量预测准确性低的问题,提出了一种基于改进粒子群算法优化极限学习机的水产养殖氨态氮含量预测模型。引入自适应变异算子改进粒子群算法的搜索性能,利用改进粒子群算法优化极限学习机的初始权值和阈值,最后训练极限学习机预测模型求得最优解。将该预测模型应用在小汤山水产品养殖系统进行有效性验证,通过试验发现,与PSO-ELM和普通BP神经网络相比,IPSO-ELM预测氨态氮含量模型有更高的精度和更好的拟合能力。结果表明,基于改进粒子群优化的极限学习机氨态氮含量预测模型简单易懂、预测精度高、易于实现,具有较好的预测性能。
关键词:氨态氮预测;粒子群算法;变异算子;极限学习机
中图分类号:TP181;S934 文献标志码: A
文章编号:1002-1302(2017)04-0183-04
养殖水质参数预测已经成为水产品集约化、精准化养殖的基础性工作,及时准确的水质预测对预防水质恶化及水产品疾病暴发有着十分重要的现实意义和经济价值[1]。氨态氮(NH3-N)含量过高是造成水体富营养化的重要因素之一,氨态氮常常以游离氨(NH3)和铵态氮(NH+4)的形式存在于养殖水体之中,若含量过高,将导致水产品抵抗力下降,呼吸困难,严重时甚至造成水产品大范围死亡[2]。虽然水体中氨态氮的含量可以在线监测,但由于养殖水体是一个大时滞的系统,存在着明显的时间延迟,氨态氮含量的变化通常滞后于鱼的生理变化[3]。因此,为了满足集约化养殖的实际需求,对氨态氮含量进行预测是很有必要的。
目前的水质参数预测在自然水体中应用得较多,养殖水质预测方面的研究较少。常用的水质预测方法有水质模拟法、专家评估法、历史平均法、回归分析法等[4-6],由于养殖水质参数之间的高耦合关系,这些方法对于模糊不确定性的养殖水质的预测精度效果不甚理想。人工神经网络[7-9]具有非常强的自适应学习能力和对非线性函数的逼近能力,可以作为构建水质预测模型的有力工具,但同时常见的前馈神经网络又存在着收敛慢、过学习、易陷入局部最优解的缺点。极限学习机[10]是一种简单易用、有效的单隐层前馈神经网络学习算法,具有学习速度快且泛化性能好的优点,很好地克服了上述缺陷。[JP+1]但是由于极限学习机初始权值和阈值的随机性,得到的结果通常不是最优解。本研究利用改进粒子群算法对极限学习机初始权值和阈值进行优化,构建养殖水质参数pH值、溶氧量、Mn含量、氨态氮含量和未来某时刻的氨态氮含量之间的非线性关系预测模型,并将该模型运用到小汤山国家精准农业示范基地水产养殖池塘,测试模型的预测精度。[JP]
1试验区域概况与数据来源
1.1试验区域概况
本試验区域是小汤山国家精准农业示范基地水产品养殖池塘,该区域每个池塘约200 m2,配备YSI6600多参数水质检测仪、增氧泵、水泵、物联网水质监控系统。物联网水质监控系统已经稳定、有效地运行了3年并且记录了大量的水质数据。
1.2数据的获取
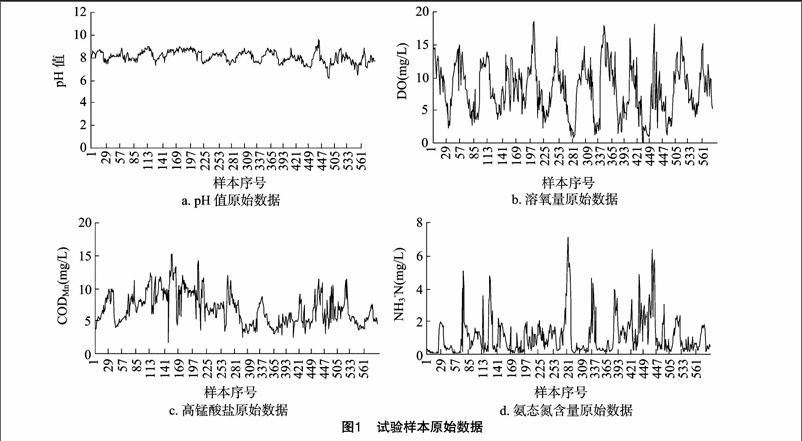
该系统采集的水质参数有pH值、溶氧量、Mn含量、氨态氮含量。本研究使用的数据来自于2015年6月7—12日,共6 d。系统的采样周期是5 min,鉴于每个周期内的数据变化不大,因此本研究选择每15 min的数据为有效值,样本总数为576组。将这些数据分成2个部分:前456组水质数据作为学习样本,供PSO-BNPP水质预测模型建模训练;后120组水质数据作为测试数据,用来检测水质预测模型的性能,原始数据如图1所示。
1.3数据的预处理
高密度水产养殖溶解氧受外界影响因素较大,若直接使用原始数据对预测模型的参数组合进行优化训练,不仅训练时间较长,同时影响所建立模型的准确性和鲁棒性,因此有必要对原始数据进行归一化操作,将所有的数据归一化到区间[0.02,0.98]中。
式中:x表示原始数据;xmax和xmin分别为数据集的最大值和最小值;x′为归一化之后的数据。
2改进粒子群算法优化极限学习机的软测量模型
2.1极限学习机
南洋理工大学黄广斌教授等在2004年提出一种简单易用、有效的单隐层前馈神经网络学习算法,即极限学习机[11-13](extreme learning machine,ELM)。在ELM中,初始权值和阈值是随机设定的,只须要设置网络的隐层节点个数,算法执行过程中不须要对网络的输入权值以及隐元的阈值进行调整,产生唯一最优解。相比于其他前馈神经网络,ELM具有学习速度快、泛化性好等优点。
对于单隐层神经网络,若有n个任意的样本(Xi,Yi),其中Xi=[xi1,xi2,…,xin]T∈Rn,Yi=[yi1,yi2,…,yim]T∈Rm,一个具有k个隐层节点的单隐层前馈神经网络可以表示为:
[JZ(]Fk(x)=∑[DD(]ki=1[DD)]βiG(Ai·Xj+Bi),j=1,…,n。[JZ)][JY](2)
式中:Ai=[ai1,ai2,…,ai3]T为输入权值,βi为连接第i个隐含层节点的输出权值,Bi为第i个隐含层节点的阈值,Ai·Xj表示向量Ai和Xj的内积,G(x)为激活函数。
若此包含k个隐含层的神经网络输出tj逼近这n个样本,使得输出误差最小,则存在Ai、Bi、βi,使得:
[JZ(]tj=∑[DD(]ki=1[DD)]βiG(Ai·Xj+Bi),j=1,…,n。[JZ)][JY](3)
简化得到
[JZ(]Hβ=T。[JZ)][JY](4)
式中:H为隐含节点的输出,β为输出权重,T为期望输出。在ELM中,由于输入权重和隐含层阈值随即给定,因此隐含层的输出矩阵[WTHX][STHX]H[WTBZ][STBZ]是固定的。训练单隐层神经网络可以转化成求解线性系统[WTHX][STHX]H[WTBZ][STBZ]β=T,β可以由式(5)确定:
式中:H+称为隐含层输出矩阵[WTHX][STHX]H[WTBZ][STBZ]的Moore-penrose的广义逆,β[DD(-1][HT6]^[DD)]表示系统的最小二乘解。
2.2基本粒子群算法
粒子群算法[14-17](particle swarm optimization,PSO)是由Eberhart和Kennedy在1995年提出,该算法是一种源于模拟鸟群觅食过程中群聚、迁徙行为的智能全局随机搜索算法。在PSO中,每一个优化问题的候选解都被记作搜索空间上的1个“粒子”,每一个粒子都有1个被目标函数决定的适应值,以及1个决定它们搜索方向和搜索距离的速度。粒子根据自身的位置和当前最优粒子的位置在搜索空间中智能调整,直至满足要求为止。
由n个粒子组成的群体对S维(每个粒子的维数)空间进行搜索,其中第i个粒子表示为Xi=(Xi1,Xi2,…,XiS),代表第i个粒子在S维空间的位置,即问题的潜在解。每个粒子对应的速度可以表示为Vi=(Vi1,Vi2,…,ViS),每个粒子在搜索时要考虑2个“极值”来更新自己,一个是本身的历史最优值Pi=(Pi1,Pi2,…,PiS),i=1,2,…,n;另一个是全部粒子的最优值Pg=(Pg1,Pg2,…,PgS),i=1,2,…,n。
在迭代过程中,粒子的速度和位置在迭代中的更新:
[JZ(]Vk+1iS=ωVkiS+c1ξ(PkiS-XkiS)+c2η(PkgS-XkiS);[JZ)][JY](6)
[JZ(]Xk+1iS=XkiS+rVk+1iS。[JZ)][JY](7)
式中:ω称作惯性权重,系保持原来速度的系数;c1和c2分别为粒子跟踪自己和整个群体最优值的权重系数;ξ和η为均匀分布在区间[0,1]内的随机数;r为约束因子。
2.3改进粒子群算法
粒子在快速向自身历史最佳位置和群体历史最佳位置的聚集过程中形成快速趋同效应,容易出现陷入局部极值、早熟收敛或者停滞的现象[18-20]。为了克服上述缺陷,本研究参照遗传算法中的算子变异思维,将PSO算法中的某些参数以一定的概率初始化。变异操作可以在扩大迭代中不断地缩小搜索范围,跳出搜索到的最佳位置,再次进行搜索,极大地降低了陷入局部极值的可能性,提高了搜索到全局最优解的概率。
2.4改进粒子群优化极限学习机预测算法
由于ELM的输入权值和隐含层的阈值是随机给定的,存在输入权值和隐含层阈值为0的情况,导致部分隐含层节点可能失效,因此在实际应用中,常常须要设置大量的隐含层节点数才能满足精度要求。同时由于ELM的初始权值、阈值都是随机生成的,因此每次训练学习结果都不一样,有时差距较大。
针对上述问题,本研究提出改进粒子群优化极限学习机预测算法(IPSO-ELM),具体步骤如下:
Step 1,初始化PSO的相关参数,包括种群数量、惯性权重、学习因子、最大迭代次数以及位置和速度的取值范围。其中,粒子的初始速度和初始位置随机赋值。
Step 2,根据输入输出信号的个数确定ELM的拓扑结构,并随机生成一组粒子群Wi=[wi1,wi2,…,wiS]T,i=1,2,…,n初始化ELM的权值和阈值,其中
[JZ(]S=S1S2+S2S3+S2+S3。[JZ)][JY](8)
式中:S1、S2、S3分别为ELM的输入层节点数、隐含层节点数和输出层节点数。
Step 3,选择ELM激活函数,根据Step 2中得到的粒子Wi对ELM权值阈值进行赋值。输入学习样本运用ELM对网络进行寻优迭代,计算每组粒子的适应度,根据初始粒子适应度值确定个体极值和群体极值,并将每个粒子的最好位置作为其历史最佳位置。
Step 4,根据公式(6)和公式(7),更新粒子的速度和位置,引入变异算子,在粒子更新之前有一定的概率初始化粒子速度和位置,计算适应度值,更新粒子的个体极值和群体极值。
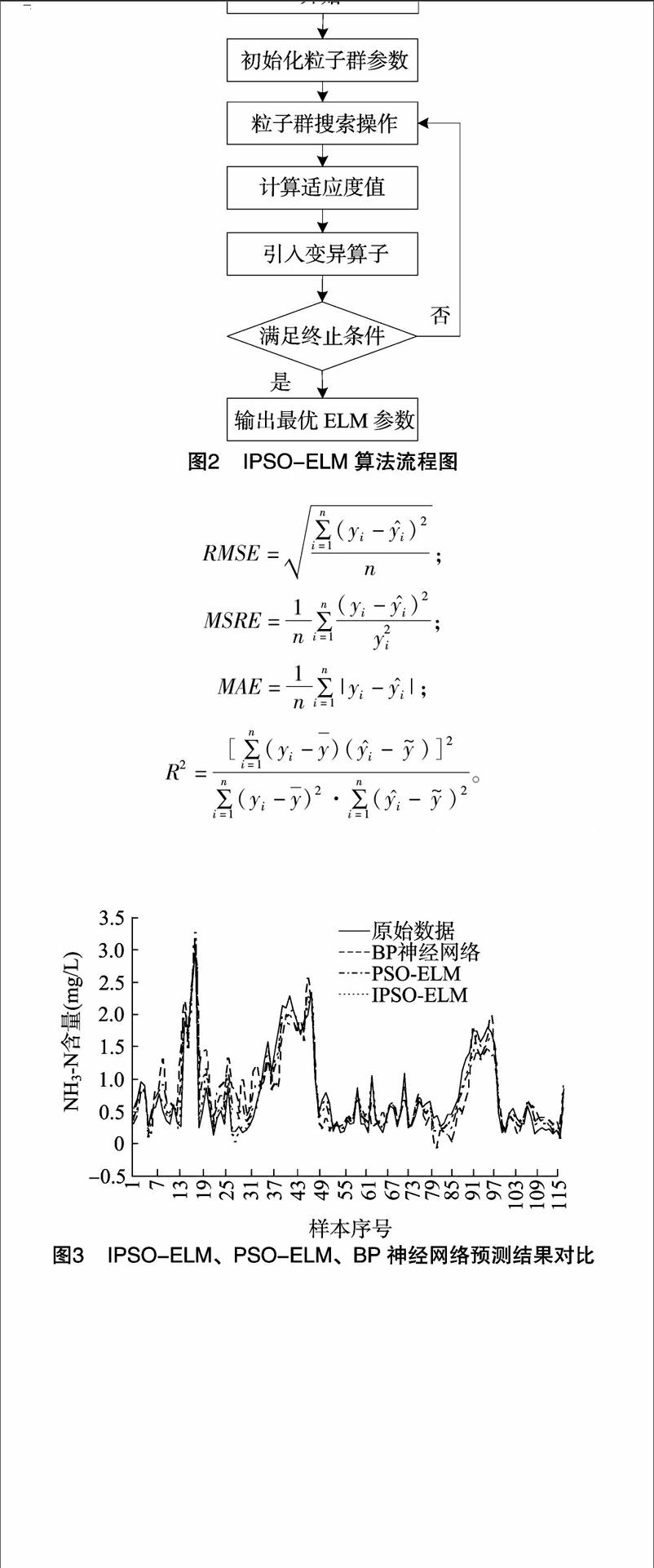
Step 5,判断是否满足结束条件,如果适应度值达到预设的精度,或者误差满足条件,或者达到最大迭代次数,则停止寻优迭代。将其解码后作为ELM的权值、阈值,经过模型训练后输出最优解;如果不满足结束条件,回到Step 4。流程图如图2所示。
[FK(W15][TPXDM2.tif][FK)]
3算法实现与试验结果分析
基于IPSO-ELM氨态氮含量预测模型的开发环境为:酷睿i5 3210M 2.49 GHz,2 GB内存,Windows XP系统,Matlab R2012a试验仿真环境。粒子群算法部分初始化:种群大小个数为35,权重系数c1=c2=1.494 45,约束因子r=0.729,算子变异概率P=0.05,迭代次數设置为50,惯性权重最大值ωmax=1.2,最小值ωmin=0.4,粒子的最大速度Vmax=5,最小速度Vmin=-1。适应度函数采用ELM的预测值和真实值之间的均方根误差(RMSE),ELM的激活函数选择Sigmoid。
3.1基于IPSO-ELM的养殖氨态氮含量预测模型
根据高密度养殖氨态氮含量预测的需要,选择每15 min的养殖水质参数数据:pH值(pHi)、溶氧量(DOi)、高锰酸盐(CODMni)、氨态氮含量为样本的数量。
3.2预测结果分析
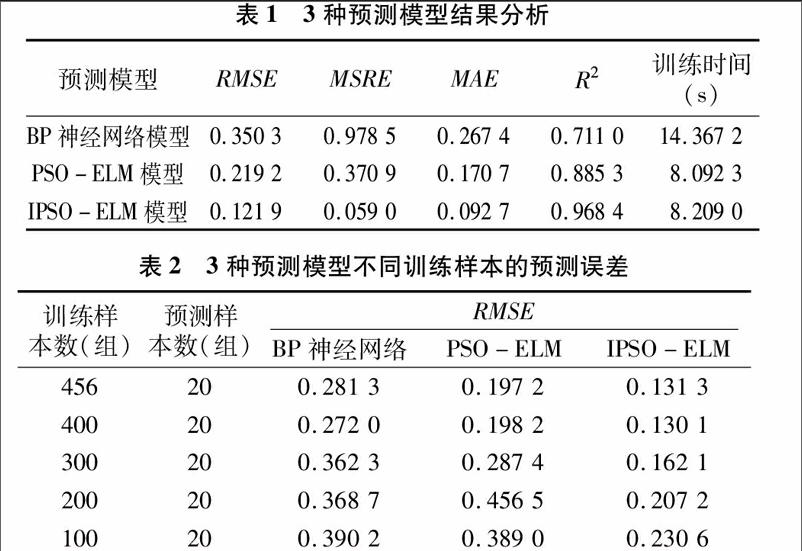
为了检验IPSO-ELM氨态氮含量预测模型的实际应用效果,选取PSO-ELM和传统BP神经网络进行对比。PSO-ELM的初始参数和IPSO-ELM的初始参数一样,BP神经网络采用4输入节点-4隐含节点-1输出节点的拓扑结构,学习率为0.086,激活函数为Sigmoid,训练次数为500次,训练目标为0.000 1。预测的结果拟合曲线对比如图3所示;表1列出了相同前提下各模型的预测误差指标分析。
基于上述分析,对于所有评价指标,本研究提出的 IPSO-ELM氨态氮含量预测模型比传统BP神经网络和 PSO-ELM模型具有更高的预测精度和较少的运行时间,可以满足高密度养殖条件下氨态氮含量预测的需求;训练样本越少,IPSO-ELM模型的预测精度比PSO-ELM模型和BP模型提高得越多,这对实现小样本预测具有重要意义。
4结论
通过对养殖水体氨态氮含量的预测,可以及时掌握氨态氮的含量以及变化趋势,为开展生态养殖环境评价、及时准确的水质预警提供基础法。本研究介绍了一种基于改进粒子群优化的极限学习机水质预测模型,引入变异算子,改善了PSO算法快速趋同效应。将其应用在时间序列上氨态氮含量预测,并同PSO-ELM模型和普通BP神经网络进行对比。试验结果表明,IPSO-ELM 预测模型对非线性时间序列上的养殖氨态氮含量预测是可行的,相比其他2种模型有更高的精度和更好的拟合能力。在IPSO-ELM模型的训练过程中,粒子群的参数决定着预测模型的精度和性能,然而目前参数的选择还是依靠经验和拼凑法,今后须在研究中进一步探讨如何获得粒子群算法的最佳参数组合,实现自适应调整。
参考文献:
[1]Huang G H,Xia J.Barries to sustainable water quality management[J]. Journal of Environmental Management,2001,61(1):1-23.
[2]何力,徐忠法,周瑞琼. 内陆渔业水质环境相关标准的应用和分析[J]. 水利渔业,2004,24(1):39-40.
[3]刘双印. 基于计算智能的水产养殖水质预测预警方法研究[D]. 北京:中国农业大学,2014:13-18.
[4]李如忠. 水质预测模式理论研究进展与趋势分析[J]. 合肥工业大学学报(自然科学版),2006,29(1):26-30.
[5]刘双印,徐龙琴,李振波,等. 基于PCA-MCAFA-LSSVM的养殖水质pH值预测模型[J]. 农业机械学报,2014,45(5):239-246.
[6]Liu S Y,Tai H J,Ding Q S,et al. A hybrid approach of support verctor regression with genetic algorithm optimization for aquaculture water quality prediction[J]. Mathematical and Computer Modelling,2013,58:458-465.
[7]梁毅,刘世洪. 基于遗传算法优化的BP神经网络的组合预测模型方法研究[J]. 中国农业科学,2012,45(23):4924-4930.
[8]朱建良,闻彦,李国辉. 基于灰色理论与BP神经网络的电力负荷预报[J]. 电机与控制学报,2006,10(4):440-442.
[9]祁金秀,陈晶. 基于粒子群算法优化的径向基函数水质预测模型[J]. 甘肃水利水电技术,2014,50(5):1-4.[HJ1.65mm]
[10]Huang G B,Zhu Q Y,Siew C K.Extreme learning machine:theory and applications[J].Neurocomputing,2006,70(1/2/3):489-501.
[11]王杰,毕浩洋. 一种基于粒子群优化的极限学习机[J]. 郑州大学学报,2013,45(1):100-104.
[12]Zong W W,Huang G B. Face recognition based on extreme learning machine[J]. Neurocomputing,2011,74(16):2541-2551.
[13]张翌晖,王贺,胡志坚,等. 基于集合经验模态分解和改进极限学习机的短期风速组合预测研究[J]. 电力系统保护与控制,2014,42(10):29-34.
[14]Ren C,An N,Wang J Z,et al.Optimal parameters selection for BP neural network based on particle swarm optimization: a case study of wind speed forecasting[J]. Knowledge-Based Systems,2014,56:226-239.
[15]粒子群算法研究[EB/OL].[2015-04-18].http://blog.csdn.net/niuyongjie/article/details/1569671.
[16]李珊. 基于粒子群算法的BP神经网络漏钢预测模型[D]. 秦皇岛:燕山大学,2014:23-31.
[17]倪庆剑,邢汉承,张志政,等. 粒子群优化算法研究进展[J]. 模式识别与人工智能,2007,20(3):349-357.
[18]黄树运. 改进的粒子群算法训练BP神经网络的研究[D]. 南宁:广西大学,2013:11-19.
[19]李松,刘力军,翟曼. 改进粒子群算法优化BP神经网络的短时交通流预测[J]. 系统工程理论与实践,2012,32(9):2045-2049.
[20]何勇,李妍琰. 改進粒子群优化BP神经网络的洪水智能预测模型研究[J].

