神经元的形态分类方法研究
李佳 陈亮


摘 要:从神经元几何形态特征的角度考虑,对神经元进行分类。由于神经元的几何形态复杂多样,直接用于分类会使得算法运行时间长、分类精度低。采用稀疏主成分分析法提取神经元的主要特征,不仅能实现几何特征的降维,减小分类难度,而且提取出的主成分部分载荷为0,使得主成分更具解释能力。依据主要特征,采用极限学习机算法对神经元进行分类。实验结果表明,该分类模型具有较高的运行效率和分类精度,能够对神经元实现有效分类。
关键词:神经元;几何形态特征;稀疏主成分分析;极限学习机
中图分类号:TP391 文献标识码:A DOI:10.15913/j.cnki.kjycx.2017.03.013
神经元,又被称为神经原或神经细胞,是构成神经系统结构和功能的基本单位。神经元形态和功能多种多样,但在结构上大致可以分成细胞体和突起两部分。突起又分轴突和树突。神经元有接受、整合和传递信息的功能。一般就长轴突神经元而言,树突和胞体接受从其他神经元传来的信息,并进行整合,
然后通过轴突将信息传递给另一些神经元或效应器。大脑是生物体内结构和功能最复杂的组织,其中包含上千亿个神经元,了解人脑对于当前的科学研究来说是一项巨大的挑战。传统的细胞生物学相关的实验室研究对于解决人脑对复杂信息的获取、处理、加工和高级认知功能的机制非常有限。人类脑计划(Human Brain Project,HBP)致力于开发现代化的信息工具,为全世界的神经信息学数据库建立共同的标准,加速人类对大脑的认识。
作为大脑构造的基本单位,神经元的结构和功能包含很多因素,其中,神经元的几何形态特征和电学物理特性是两个重要方面。电学特性包含神经元不同的电位发放模式;几何形态特征主要包含接受信息的树突、处理信息的胞体和传出信息的轴突三部分。鉴于树突、轴突的生长变化,神经元的几何形态千变万化。电学特性和空间形态等多个因素一起综合体现了神经元的信息传递功能。要想加深对大脑的研究,应先认识神经元的特性,实现神经元的分类。
神经元的分类有多种方法,常以神经元突起的数目、功能和所释放的递质进行分类。根据神经元突起的數目可以分为假单极神经元、双极神经元和多极神经元;根据神经元的功能,
可将其分为感觉神经元、运动神经元和中间神元;按照释放的递质的不同,可将其分为胆碱能神经元、胺能神经元、氨基酸能神经元和肽能神经元。
本文基于神经元的几何形态,利用神经元的空间几何特征,通过稀疏主成分分析和极限学习机建立神经元的分类模型,提出神经元的一个空间形态分类方法,并将神经元根据几何形态进行了较为准确的分类。
1 稀疏主成分分析
神经元的形态复杂多变,大量的参数从不同的角度刻画了
神经元的形态特征。此外,在实际研究中,对象的特征不会直
观显示出来,而需要从中提取。为了全面表示对象,在特征提取的过程中,可能尽量选择比较多的特征变量,以防对象特征的丢失。这就容易出现2种情况:①为了避免遗漏重要信息而选择尽可能多的特征;②随着特征的增多增加了问题的复杂性,同时,造成信息的大量重叠。鉴于此,需要合理处理并提取数据,在尽可能代替原始变量的所有信息的同时,还要求减少处理后的变量数。
主成分分析是一种广泛应用于工程学、生物学和社会科学等领域的数据处理与统计降维的方法,它可以将原来变量重新组合成一组新的互相无关的几个综合变量。然而,主成分分析存在一些不足之处,由于每一个主成分都是其他原始变量的线性组合,也就是说主成分依赖于所有原始变量,因此,很多时候主成分难以作出解释。用主成分分析处理某些实际问题时,往往只能给出数据的统计、解释,而很难给出对应的实际意义的解释。
Zou.H提出了一种新的方法——稀疏主成分分析。该方法将主成分的求解问题转化为LASSO(Least absolute shrinkage and selection operator)回归问题,因此,稀疏主成分的求解就有效转化为线性模型的变量选择问题。在此基础上,引入弹性网(E-lasticNet)惩罚结构,提出了稀疏主成分分析方法。其计算步骤如下。
3 实验与分析
本文使用的神经元数据来自于Neuronmorpho.Org网站。根据神经元的特征描述,选取神经元的胞体表面积、干的数目、分叉的数目等20个空间几何特征量,采用稀疏主成分分析法对数据进行降维处理,研究神经元的分类。
表1为神经元的20个几何特征参数的含义及计算方法。
选取7类神经元的空间几何数据记为数据集D,共选取98个样本进行实验。其中,70个样本为训练集Dtr,28个样本为测试集Dte,用于训练ELM网络。具体实验步骤如下:①数据预处理,对数据集D进行标准化处理;②利用稀疏主成分分析对数据进行降维,提取主要特征;③ELM训练,给定训练样本集的特征向量xi和类别标签ti,设置隐层结点的个数N0,ELM随机产生输入权值wi和偏值bi,求解输出权值;④ELM测试,输入未知样本的特征向量,利用ELM训练时求解得到的输出权值矩阵β构建分类模型。
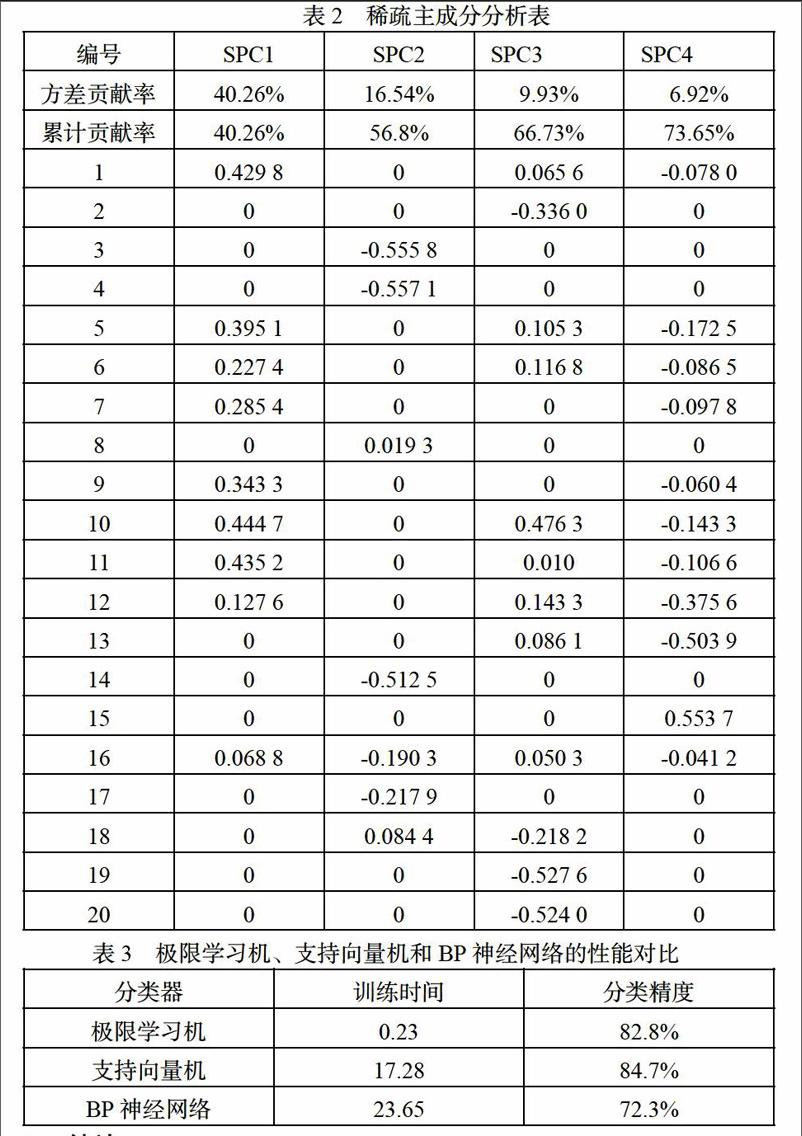
表2给出了稀疏主成分的分析结果,前4个稀疏主成分的累计贡献率超过70%,因此,神经元的20个形态特征可以用4个主成分来表示。从几何形态的意义上分析,4个主成分表征了神经元的4个方面,即:①第一主成分SPC1反映了胞体的表面积、宽度、高度、深度、长度、表面积和体积7个特征,表征了神经元的空间形态的几何轮廓信息;②第二主成分SPC2反映了分叉数目、分支数目、分支级数、破碎程度、非对称分化5个特征,表征了神经元空间形态的分支分叉的相关信息;③第三主成分SPC3反映了干的数目、直径、罗尔比率、局部分叉角和远端分叉角5个特征,表征了神经元空间形态的房室和分叉角度的相关信息;④第四主成分SPC4反映了欧式距离、路径距离、压缩比3个特征,表征了神经元空间形态的伸缩性。
为了验证提出的神经元形态分类方法的有效性,对比极限学习机、支持向量机和BP神经网络的性能,结果如表3所示。其中,支持向量机采用libsvm工具箱,BP神经网络采用MATLAB神经网络工具箱。由表3可知,极限学习机的分类精度与支持向量机有微小的差距,但是,训练速度远快于支持向量机和BP神经网络。支持向量机和BP神经网络训练参数耗时比较长,如果训练样本较大,则二者的训练会非常缓慢;极限学习机只要给定合适的隐层结点数目,就能获得良好的分类性能,并一次求得全局最优解,泛化性能好于BP神经网络。
4 结论
从神经元的空间几何形态出发,利用稀疏主成分分析法对神经元的几何特征进行降维,通过原变量的少数几个线性组合来解释原变量的绝大多数信息,大大减少了分析时变量的维数,增强了主成分的可解释性,为后续分类奠定了良好的基础。在稀疏主成分分析的基础上,采用ELM算法对神经元分类,实验结果表明,ELM算法的分类精度比较高,相比于支持向量机和BP神经网络的训练速度更快,能够对神经元进行有效分类。
参考文献
[1]Shepherd G M,Mirsky J S,Healy M D,et al.The Human Brain Project:neuroinformatics tools for integrating,searching and modeling multidisciplinary neuroscience data.Trends in Neurosciences,1998,21(11):460.
[2]Jiang R,Liu Q,Liu Q,et al.A proposal for the morphological classification and nomenclature of neurons. Neural Regeneration Research,2011,6(25):1925-1930.
[3]Wang T,Liao D.Neuronal morphology classification based on SVM.International Conference on Computer Science and Service System.IEEE,2011:3344-3347.
[4]尚小晶,劉小梅,李成凤,等.神经元的几何形态分类[J].吉林大学学报(信息科学版),2011,29(3):237-244.

