石墨烯中的量子输运性能简析

赵珊

摘 要：石墨烯作为目前发现的最薄、导电导热性能最强、结构强度最大的新型纳米材料已经广泛应用于各个领域，其中，最有潜力的应用则是成为硅的替代品。所以，对石墨烯中量子输运性能分析与建模已经成为当今的研究热点。文章采用从相对论流体磁动流体力学出发，结合Boltzmann方程（BTE）推出石墨烯的流体力学方程，引入剪切粘度与雷诺数（Reynolds number）作为石墨烯输运性能分析指标，表明了石墨烯作为纳米材料的优异性能。

关键词：石墨烯；量子输运；流体力学方程；剪切粘

石墨烯由于其准粒子的无质量相对分散特性和高迁移率吸引了各界关注，并且它还显示出了一系列优异的性质，如：超高的导电率[1]；剪切粘度与熵之比超低[2]；不仅有特殊的结构强度，而且结合了力学灵活性[3]和光透明度[4]。最近的研究显示石墨烯提供了一种特有方式，去观察在适度的高温下，极端相对论粒子的等离子体输运特性[5]。如将纯石墨烯设在一个特定的参数空间，则其费米表面收缩至两点，且在许多其他方面的表现，也与接近更复杂量子临界点的系统非常相似[6]。由于石墨烯的无质量狄拉克（Dirac）粒子，其相对极端夸克-胶子等离子体性质也很特别。通过对这些性质的分析和计算可以推导出其流体力学方程。

1 性能介绍

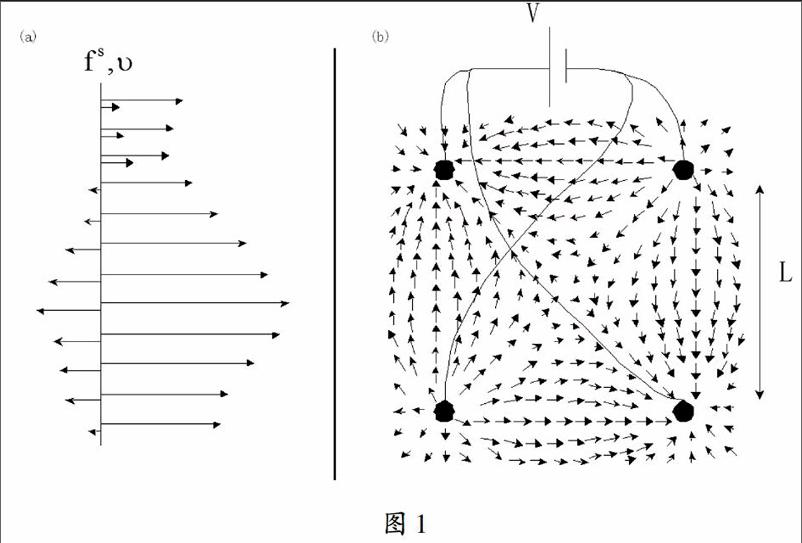
剪切粘度η用来测量流体阻值，从而建立横向速度梯度，见图1，粘度越小则其流体力学越趋于复杂。类似于导体的电阻率，粘度通过降低速度场中的多相性而引出熵增率。虽然η=0的理想流体不存在，但能找到非常接近于理想流体的完美的流体。

（b）在一个分源点和漏极点保持在±V/2的四点几何形中，不均匀电流的预期分布。当没有粘性和其他非局域效应时，电流将与外加电压V成比例，与两点之间的距离L无关，而粘性效应随着L减小而减小。

粘度的单位为？捩n，其中，n表示密度。为了量化剪切密度的大小，通常将η/？捩与热激励nth比较，nth可以通过熵密度计算，s～kBnth。受石墨烯在RHIC实验[7]中优异性能的启发，Kovtun等人提出广泛系统中η与s之比的下限[8]：

由于在无碰撞的光学区间？捩ω>>kBT[12]内，电子间相互作用对导电性σ（ω，Τ）的影响非常小，而在相反区间？捩ω<

石墨烯中，当能量低于几个电子伏，其电子特性则如Hamiltonian所示：

其中，费米速度υF≈108cm/s， 为动量算子，l=1，…，N为N=4自旋和谷自由度的下标，σ（σx，σy）为Pauli矩阵在蜂巢晶格结构两个底晶格空间的表示。如果没有库伦相互作用，公式（2）则变成自由无质量狄拉克粒子的N类Hamiltonian[14]。

2 流体力学方程推导

接下来讨论在存在库伦相互作用的相对论流体磁动流体力学，在流体力学模型中的响应函数适用于在狄拉克点附近的石墨烯[17]。特征速度υF≠c决定了相对分散，在流体中的（反）粒子的电荷为±e。下面采用υF=e=？捩=1为单位。

由于库伦作用传播速度约为光速c>>υF，所以可认为它是瞬时的，则很显然通过将实验框架设为一个特定的参照系，打破了流体的相对不变性。

上述表达式包含了耗散项νμ，？子μν用来计算热电流和粘性力，P代表压强，ρ代表电荷密度。若无粘性项，则在流体元在类空间入口的压力以及在类时间入口的能量密度这样的静止参考系中，应力能量张量为一个对角矩阵。坐标系中各分量为：

T00=ε，（5）

其中，ε，P，ρ为局域化学势μ（r）的函数，ε表示能量密度，局域温度T（r），磁场为B，μ（r）包含了由不均匀的电荷分布而引起的库伦势。

电荷、能量及动量守恒如下：

其中，电磁场张量，

包含一个由于系统本身的不均衡电荷密度而自发产生的空间变化场：

其中，式（14）中已将统一的本底电荷密度减去。

在坐标系中线性守恒定律则明确表示为：

此外，包含了一个由于微弱杂质散射而产生的弛豫时间τ。电流的本构方程如下：

基于上述推导出的流体力学方程以及石墨烯中电子的量子BTE，分析出了传输系数——流体剪切粘度[18]，也即下述模型中的输入参数。当电子-电子间相互作用主导无弹性散射率时，即低杂质、高温且稳定场情况下，流体力学方法就能有效应用于石墨烯[19]。为了忽略电子-声子间作用，选择在100K左右的合适高温区间[20]。无磁场时，即B=0，准粒子分布函数为f，由BTE，则：

其中，-Ω[f]表示考虑电子-电子间相互作用的碰撞项，

则式（17）、（18）、（19）、（20）可推导为：

其中，式（23）为电荷守恒，式（24）为能量密度守恒，式（25）为动量守恒，ρr≡（ε+P）/υF2。

3 性能分析

对于纯石墨烯（μ=0），电荷密度由于热能而存在，则可写成，

然而，当石墨烯掺杂时，杂质会使石墨烯样品产生电位，此时，则必须要考虑由于化学势产生的修正，

其中，Φρ为无量纲递增函数。

式（25）中的剪切密度η可由下述方程計算：

其中，Cη～Ο（1）为一个数值系数。熵密度可由Gibbs-Duhem关系ε+P=Ts计算，此等式是在|■|<υF的假设下推导出来的，因此相对修正项∝？坠P/？坠t可忽略，而恢复为经典的Navier-Stokes方程。所以，尽管电子速度很快，|■|～0.1υF，但由于样品的纳米级尺寸和石墨烯中电子流的高剪切密度，雷诺数依然稳定。

基于式（25），線性尺寸为L0的石墨烯样品其动态粘度由式（28）给出，此等式可写成以下形式：

其中，引入特征频率ωf=υF/L0，通过解合适的量子BTE，得Cη？勰0.45[21]。式（29）也可以写成η=Cηqf-2 ？捩/L02，qf≡？捩ωf/（kBT）。由此，为了应用经典电子流体力学描述，激励能量必须远低于热能，即qf<<1，也是所谓的碰撞主导模式。拿一组特定参数，υF=106，L0=10-6，T=100K，η/s～0.2？捩/kB，则得到η～10-20。因雷诺数由流体的动力粘度，而非动态粘度所决定，则就不涉及质量密度，这有利于估算石墨烯中电子流体的动力粘度。

为了达到这个目的，鉴于式（25），定义雷诺数为：

其中，ν0=υFL0。通过将雷诺数写成Re=υ0L0/ν，与上述方法类似，可得到：

利用η/s=0.2？捩/kB3，qf？勰0.07，则得到ν？勰10-2。尽管石墨烯动态粘度极低，但石墨烯的动力粘度依然大约比水的动力粘度大四个数量级。这四个数量级的差距是由于电子的高速而产生的，也即电子的高速是雷诺数产生高值的最终决定因素。

4 结束语

在本文中，忽略了电子-杂质及电子-声子的相互作用，仅基于对石墨烯中的电子流体力学方程描述，对其剪切粘度、动力粘度、动态粘度及雷诺数进行了探讨，表明石墨烯具有低剪切粘度与熵密度之比、高动力粘度以及低动态粘度。而通过对石墨烯动力粘度的分析，可以看出，在微米级的比例下，雷诺数可以在石墨烯样品中实现高值。在后续的研究工作中，还将对电子-声子、电子-杂质和声子-声子建模及量子输运性能分析。

参考文献

[1]Novoselov， K. et al. Two-dimensional gas of massless Dirac fermions in graphene[J].Nature Letters 438，197（2005）.

[2]Muller， M.， Schmalian， J. & Fritz， L. Graphene： A nearly perfect fluid[J]. Phys. Rev.Lett. 103，025301（2009）.

[3]Lee， C.，Wei， X.， Kysar， J. W. & Hone， J. Measurement of the elastic properties and intrinsic strength of monolayer graphene[J]. Science 321，385-388（2008）.

[4]Kuzmenko， A. B.， van Heumen， E.， Carbone， F. & van der Marel， D. Universal optical conductance of graphite[J]. Phys. Rev. Lett. 100，117401（2008）.

[5]L. Fritz， J. Schmalian， M. Muller， and S. Sachdev.Lifshitz hydrodynamics[J].Phys.Rev. B 78，085416（2008）.

[6]D. E. Sheehy and J. Schmalian， Phys. Collective excitations in graphene in magnetic field[J].Rev. Lett. 99，226803（2007）.

[7]E. Shuryak.Physics of strongly coupled quark-gluon plasma[J]. Progress in Particle and Nuclear Physics 53，273（2004）.

[8]P. Kovtun， D. T. Son， and A. O.Ratio of viscosity to entropy density in a strongly coupled one-component plasma[J]. Starinets， Phys. Rev.Lett. 94，111601（2005）.

[9]Geim， A. K. & MacDonald， A. H. Graphene： Exploring carbon flatland[J]. Phys.Today 35（2007）.

[10]A.F. Ioffe and A. R. Regel， Prog.Anderson localization and superconductivity. Semicond. 4，237（1960）.

[11]S. Sachdev， Quantum Phase Transitions[J]. Cambridge University Press， Cambridge （1999）.

[12]I. F. Herbut， V. Juricic， and O.Vafek， Phys. Interaction corrections to the minimal conductivity of graphene via dimensional regularization[J].Rev. Lett.100，046403（2008）.

[13]A. B. Kashuba， Phys. Rev.Conductivity of defectless grapheme[J]. B 78，085415（2008）.

[14]P. R. Wallace， Phys.Effect of doping on photovoltaic characteris

tics of grapheme[J]. Rev.71，622（1947）.

[15]J. Gonzalez， F. Guinea， and M. A. H. Vozmediano， Nucl.Phys.Non-Fermi liquid behaviour of electrons in the half-filled honeycomb lattice[J]. B 424，595（1994）； Phys. Rev. B 59，R2474 （1999）.

[16]J. Ye and S. Sachdev.The effects of weak disorders on Quantum Hall critical points[J]. Phys. Rev. Lett. 80，5409（1998）.

[17]Markus Muller and SubirSachdev.Collective cyclotron motion of the relativistic plasma in grapheme[J].Department of Physics.MA 02138（2008）.

[18]Novoselov， K. S. et al. Electric Field Effect in Atomically Thin Carbon Films[J].Science 306，666-669 （2004）.

[19]Muller， M.， Fritz， L. &Sachdev， S. Quantum-critical relativisti

c magnetotransport in graphene[J]. Phys. Rev. B 78， 115406（2008）.

[20]Bao， W. S.， Liu， S. Y.， Lei， X. L. &Wang， C. M. Nonlinear dc transport in graphene[J]. Journal of Physics： Condensed Matter 21，305302（2009）.

[21]M. Mendoza1， H. J. Herrmann& S. Succi，Hydrodynamic Model for Conductivity in Graphene[J].Freiburg Institute for Advanced Studies， Albertstrasse， 19，D-79104（2013）.