复模态参数的特征曲线法及其应用研究

于 澜，李启伦

(1.长春工程学院理学院，长春 130012； 2.长春工程学院国际教育学院，长春 130012)

复模态参数的特征曲线法及其应用研究

于 澜1，李启伦2

(1.长春工程学院理学院，长春 130012； 2.长春工程学院国际教育学院，长春 130012)

提出了复模态参数特征曲线法。利用多节点数值技术，绘制复频率、复模态及复模态的一阶灵敏度的曲线，对具有代表性的复模态参数特征曲线的几何性态进行分析，不仅有利于结构优化与控制，而且可以有效地检验灵敏度的精度。利用一个具有7自由度的卡车集成结构系统来展示该方法的有效性及可行性。

复模态参数；灵敏度；特征曲线；三次样条插值

0 引言

在结构振动分析中，常需求解广义特征问题(s2M+sC+K)u=0，其中K、C和M是结构的刚度、阻尼和质量矩阵，s为复频率，u为复模态向量，二者统称为复模态参数。一个结构的动力特性可以用它的复模态参数进行完整地描述，复模态参数在分析系统结构的性能及振动响应等方面起到重要的作用，因此，对它们的研究伴随着工程应用的设计[1]、分析[2]、修正[3]、损伤识别[4]等各个方面。

灵敏度即求导信息，它是一种度量，是一种评价由于设计变量或参数的改变而引起结构特性变化的程度的方法。结构系统的灵敏度分析的主要目的是确定设计参数变更时，系统响应、复频率及复模态向量等发生的变化率，因此，通过灵敏度分析可得到为实现最优化、修正和损伤识别等目标所需要的设计导数。灵敏度分析算法的研究趋势表明，目前较为活跃的几种方法是：1)模态法[5-7]；2)代数法[8]；3)直接法[9]；4)迭代法[10]。前两类方法为精确算法，后两类方法多数为近似算法。针对前两种精确算法，因为模态法的精确计算要求使用全部模态，一旦采用截模态算法，就成为近似算法了，但全模态算法的计算量较大。代数法的计算难点出现在解方程组的环节中，一旦采用解方程组的数值技术，也必然获得的是灵敏度近似解。因此，计算灵敏度的精度与验算问题是一个难点。目前绝大多数多自由度系统的灵敏度算法，包括有阻尼或无阻尼，它们的验证方法都是将灵敏度计算结果与差分灵敏度结果或泰勒近似值相比较，却很难与灵敏度精确值相较。与此同时，随着数值技术和计算机技术的不断进步，我们开始思考，求得的模态参数的灵敏度虽然是单节点处的，但它反映的却是模态参数在随设计参数连续变化过程中所发生变化的趋势和程度，那么它的有效性和可靠性必定还是要在模态参数本身的变化样貌中得以印证。

为此，本文提出了一种新的研究复模态参数变化及其与灵敏度之间关系的新方法，即复模态参数的特征曲线法，简称为复特征曲线法，并在一个复杂阻尼结构的动特性分析中得以应用和展示。

1 复特征曲线法

复特征曲线法是指首先依据结构在设计参数的某点处计算其复模态参数及复模态的一阶灵敏度的算法公式，在设计参数的某连续变化的可行域内，利用多个节点处计算复模态参数及复模态的一阶灵敏度的离散值，然后用数值方法拟合整个可行域内复模态参数及复模态的一阶灵敏度随设计参数变化而变化的函数曲线，最后根据灵敏度的几何意义及函数曲线的几何性态来分析结构设计中需要了解的各种信息。可见，复特征曲线法是在一个设计参数的可行域内，通过多节点灵敏度分析，来发现和分析特征对象的变化特点及规律的一种新的手段。在此之前，通常我们计算灵敏度时，都是在一个节点处进行，那么数据是静止的，依据本文方法将再次利用这些灵敏度信息，把对灵敏度信息的掌握程度转化为更为经济的价值来源。从数据变化和行进轨迹来预测可能发生的改变或即将维持的稳定，从单纯依靠灵敏度数据的精度，转变为对灵敏度数据的相对比较和动态观测。当然，我们不是放弃了对每个节点处的灵敏度更高精度的计算追求，只是不过多地沉迷于此，尤其是当对精度追求变得不太可行的时候，更多的努力应放在宏观层面上，将使我们拥有更强的洞察力。

复特征曲线法包含着对3条特征曲线的分析：

1)复频率曲线：这条曲线的绘制意义在于，我们可以寻找设计区间内复频率的相互逼近、远离及稳定等规律，以及对复频率进行分区等。

2)复模态曲线：绘制这组曲线的目的，首先是用来发现设计区间内复模态的跳跃、弯转及尖峭等现象，这些现象所包含的意义目前还不是十分清楚，但至少发现这些现象是个良好的开端；其次是用来检验复模态的一阶灵敏度的计算精度。

3)复模态的灵敏度曲线：首先利用这组曲线更有助于我们理解复模态跳跃、弯转及尖峭等动态行为；其次从数值角度把握这些变化的程度(即变化率)；再者可用于检验复模态的二阶灵敏度的计算精度，因此具有十分重要的价值。

工程设计分析的目的并不止于此，我们希望了解与结构的动力特性变化相关的因素，当这些特征曲线已经表征了特征值与特征向量的变化规律时，我们最关心的当然是这些因素的变化与结构动态行为变化之间的相关程度，剔除相关度小的影响因素，聚焦那些相关度大的影响因素，从而实现更好地把握结构控制规律的目标。

2 复频率及复模态曲线

对N自由度阻尼振动系统，自由振动方程为

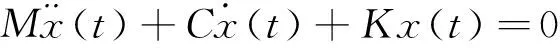
(1)

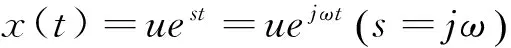
(2)

对于N自由度振动系统，特征方程

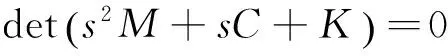
(3)

3 复模态的灵敏度曲线

随着研究的深入和工程应用的发展，在模态参数灵敏度分析的实施过程中还可能面临着一些新问题，例如按系统性质矩阵的对称与非对称性分类，或按实或复频率的性态分为单频、重频及密频系统[11]，再者依据实或复模态空间的特点还要考虑完备[5]及亏损[12]两种情况等等。在具体的应用过程中由于系统的复杂性[13]，可能这些分类方法还存在多种形式的交叉。下面以最简单的对称单频阻尼系统的复模态参数的灵敏度分析为例，展示复特征曲线法的基本思路、步骤和分析方法。而对于其他类型的结构，除了在计算灵敏度的算法方面有所区别外，有关复特征曲线法的基本思路、步骤和分析方法这一方面的内容基本是一致的。

如果系统的复频率全不相同，那么称之为单频系统。对这样的系统。存在规范正交关系为

ΦTAΦ=E，

(4)

ΦTBΦ=diag(-s1，…，-s2N)，

(5)

其中状态向量矩阵为Φ=[φ1，φ2，…，φ2N]，状态向量为

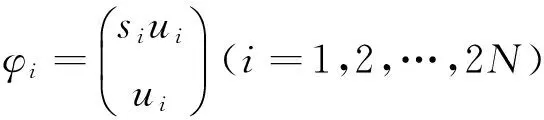
(6)

且

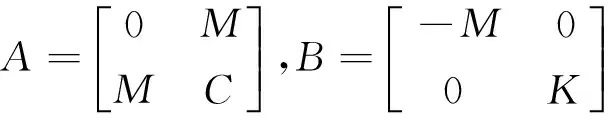
所满足的广义特征矩阵方程为

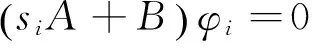
(7)

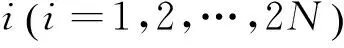
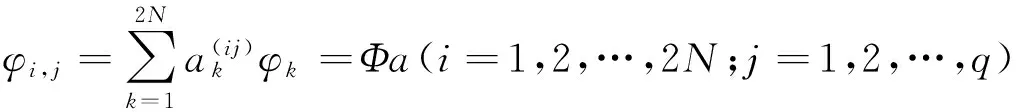
(8)

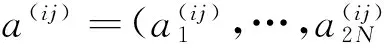
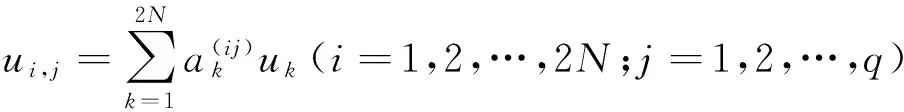
(9)

其中

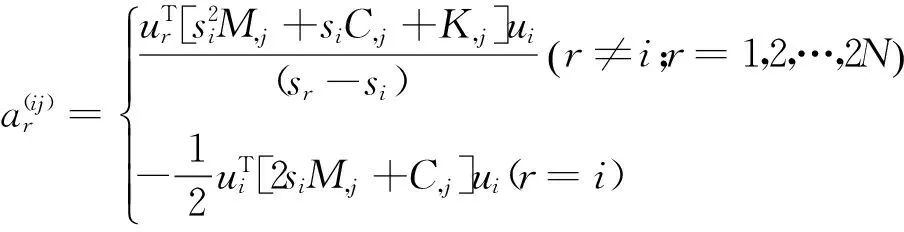
(10)

代入式(9)就可求得复模态ui(i=1，2，…，2N)的一阶灵敏度ui，j(j=1，2，…，q)。

这种利用灵敏度进行结构分析的方法不仅有利于观察复模态参数本身的变化特点，而且具有较为明显的数学意义。在系统(1)的某设计参数的可行域内，用复模态一阶灵敏度的计算值作为采样值，可绘制复模态的灵敏度曲线。

4 复特征曲线法在复杂阻尼结构中的应用

4.1 复频率曲线

首先利用式(2)将m5从1 782 kg变化至1 818 kg，每隔2 kg取为节点采样系统复频率数据，并分别利用三次样条插值绘制这些复频率的实部和虚部的拟合曲线图如图2和图3所示，因为系统的14个复频率呈复共轭对出现，所以只需考虑s1，s3，s5，s7，s9，s11，s13即可。

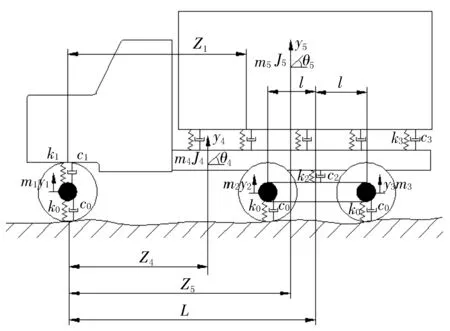
图1 卡车集成结构系统

m5图2 复频率的实部曲线图

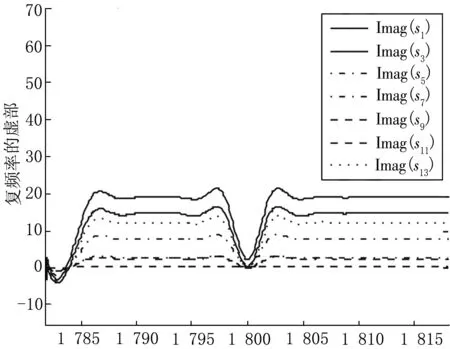
m5图3 复频率的虚部曲线图

4.2 复模态曲线

利用式(2)将m5从1 782 kg变化至1 818 kg，每隔2 kg取为节点来采样系统复模态向量数据。然后利用式(6)构造状态向量，依据式(4)规范化状态向量后，取状态向量的后N维，即为满足式(2)和式(4)的复模态向量数据。因为系统的14个复模态向量呈复共轭对，所以只需考虑u1，u3，u5，u7，u9，u11，u13即可，本文仅以u1，u3，u5为例分别利用三次样条插值绘制这些复模态数据的实部和虚部的拟合曲线图，如图4～9。

m5图4 复模态u1的实部曲线图

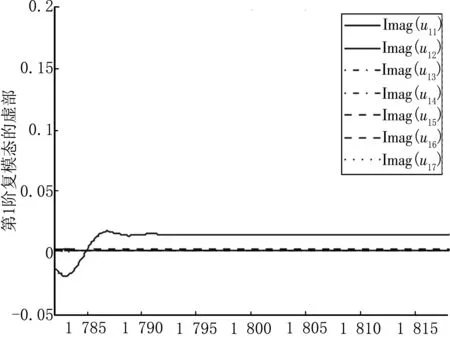
m5图5 复模态u1的虚部曲线图

m5图6 复模态u3的实部曲线图

由图4～9可见，复模态在复频率出现密集现象的范围内，也发生了弯转和跳跃，而在其他复频率稳定的范围内复模态也较为稳定。

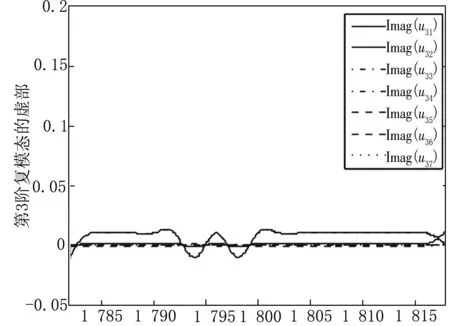
m5图7 复模态u3的虚部曲线图

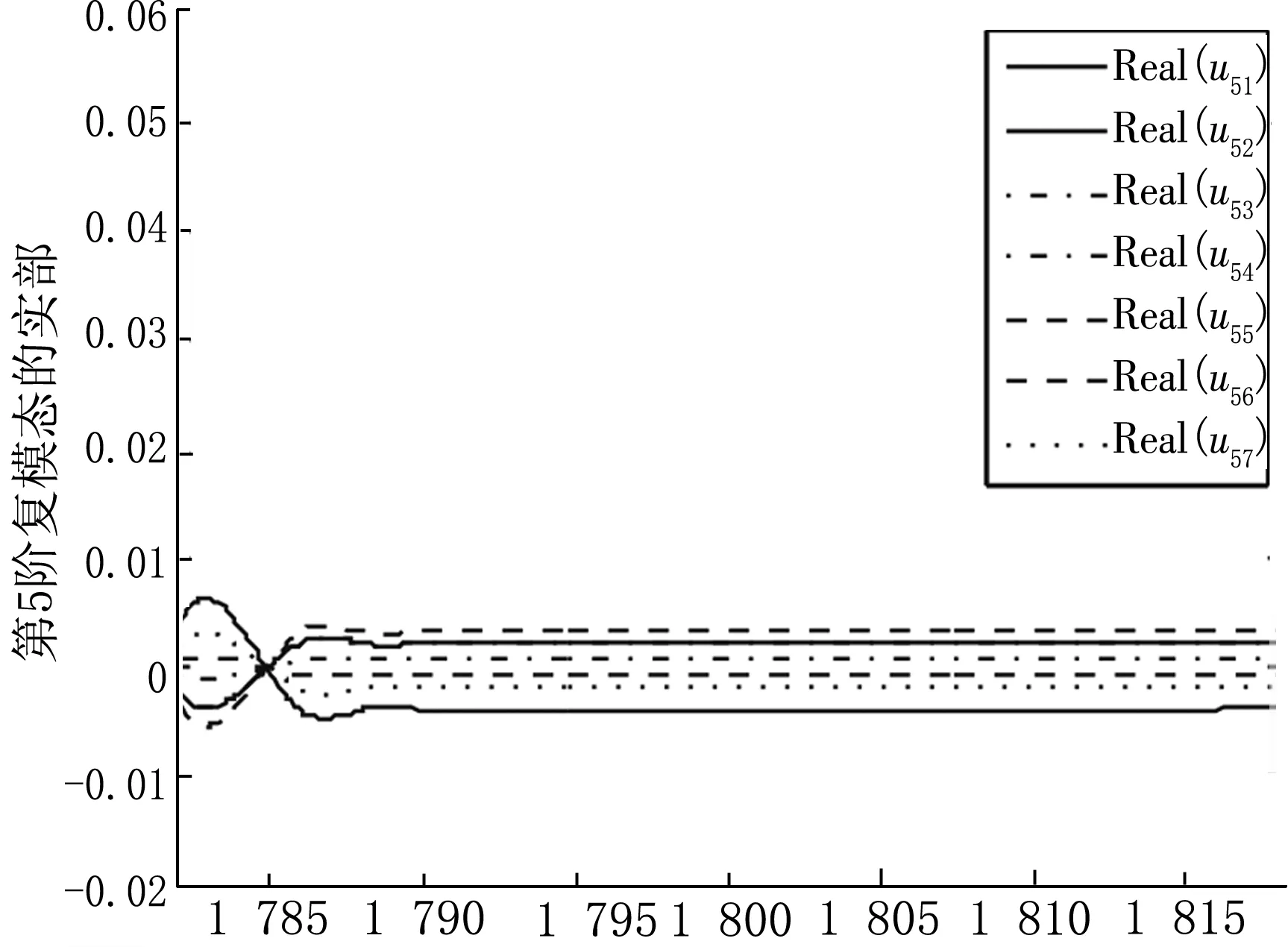
m5图8 复模态u5的实部曲线图

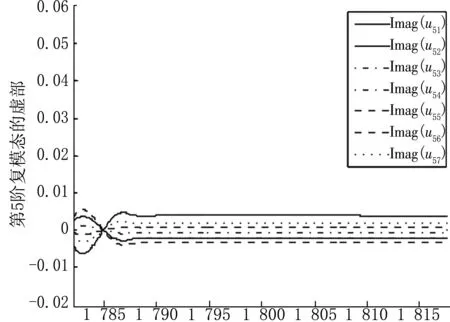
m5图9 复模态u5的虚部曲线图

4.3 复模态的灵敏度曲线

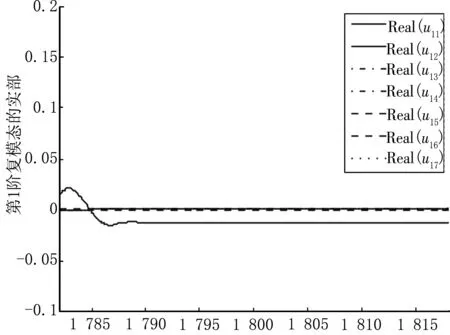
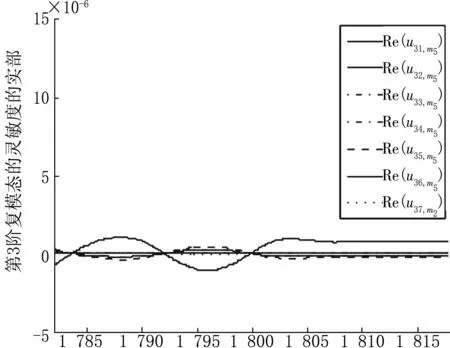
将m5从1 782 kg变化至1 818 kg，每隔2 kg取为节点，在每个节点处利用式(10)计算一阶灵敏度系数，代入式(9)获得系统复模态灵敏度向量数据。因为系统的14个复模态向量呈复共轭对，所以只需考虑u1，m5，u3，m5，u5，m5，u7，m5，u9，m5，u11，m5，u13，m5即可，本文仅以u1，m5，u3，m5，u5，m5为例，分别利用三次样条插值绘制这些复模态灵敏度数据的实部和虚部的拟合曲线图，如图10～15。

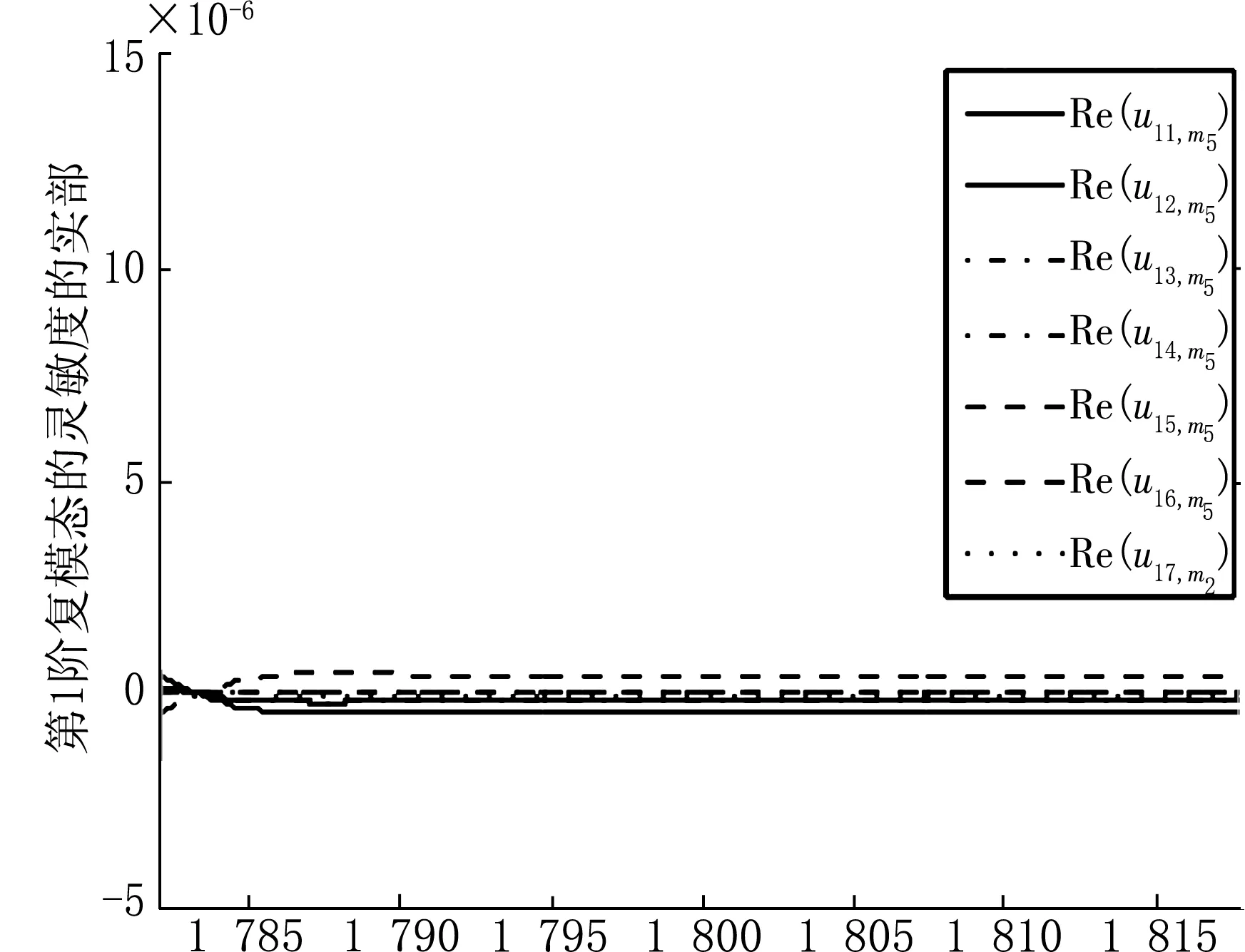
m5图10 复模态u1的灵敏度实部曲线图

m5图11 复模态u1的灵敏度虚部曲线图

m5图12 复模态u3的灵敏度实部曲线图

观察图10～15，首先注意到复模态的灵敏度的数量级，可见灵敏度非常小，反映出复模态的稳定性；其次在复模态发生跳跃及弯转的位置，其灵敏度也确实发生了相对较大的变化，这说明复模态的一阶灵敏度在反映复模态的几何性态方面是比较有效的。因为灵敏度毕竟属于局部特性，因此适当加大灵敏度值的采样密度，能够更为全面地反映复频率及复模态随设计参数变化而变化的动态特征。

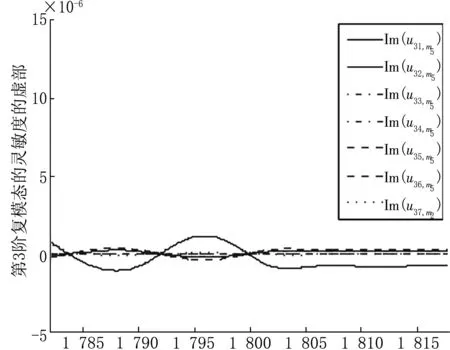
m5图13 复模态u3的灵敏度虚部曲线图

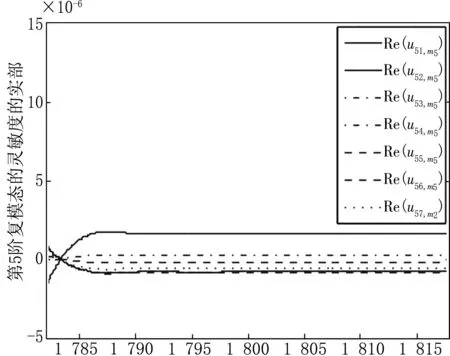
m5图14 复模态u5的灵敏度实部曲线图

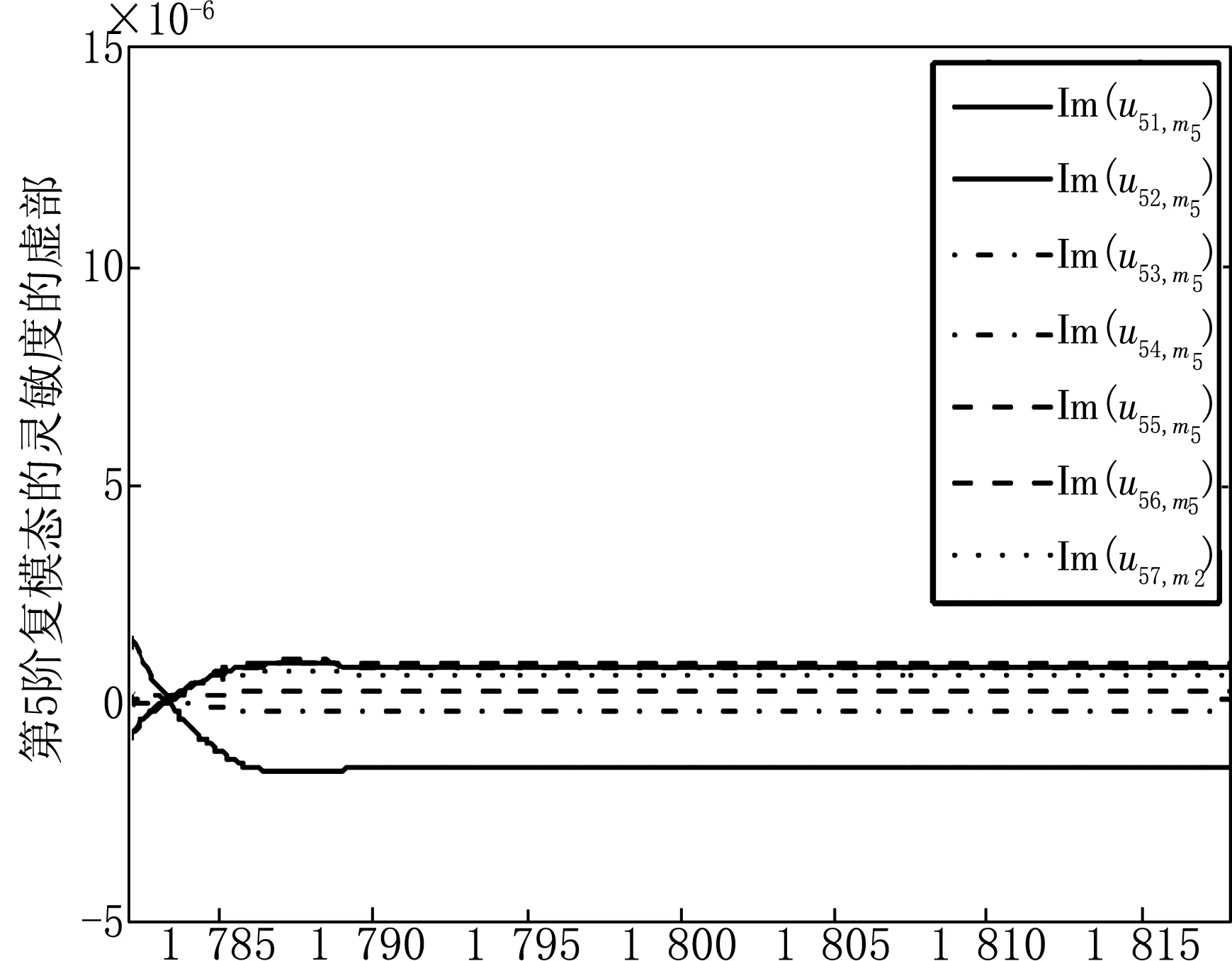
m5图15 复模态u5的灵敏度虚部曲线图

5 结语

本文提出了复模态的特征曲线法，在一个7自由度的卡车集成结构系统中，应用复模态特征曲线法，首先绘制了复频率及复模态向量与设计参数的关系图来分析设计参数对系统状态的影响，尤其是研究发生复频率重复现象时，复模态向量的变化特点；再利用复模态向量关于设计参数的灵敏度曲线图来分析和验证上述结果，表明复模态参数的灵敏度分析确实能在很大程度上反映结构性态。

[1] 张淼，于澜，鞠伟.基于频响函数矩阵计算阻尼系统动力响应的新方法[J].振动与冲击，2014，33(4)：161-166.

[2]XieYM，StevenCP.Evolutionarystructuraloptimizationfordynamicproblems[J].ComputersandStructures，1996，58:1067-1073.

[3]ChoukseyM，DuttJK，ModakSV.Modelupdatingofrotorssupportedonjournalbearing[J].MechanismandMachineTheory，2014，71:52-63.

[4]Sheng-EnFang，RicardoPerera，GuidoDeRoeck.Damageidentificationofareinforcedconcreteframebyfiniteelementmodelupdatingusingdamageparameterization[J].JournalofSoundandVibration，2008，313:544-559.

[5] 张淼，于澜，鞠伟.重频结构模态灵敏度分析的高精度截模态算法[J].振动工程学报，2014，27(4):526-532.

[6] 张淼，于澜，鞠伟.重频系统的频率灵敏度分析算法研究[J].华南师范大学学报:自然科学版，2014，46(3)：39-43.

[7]MoonYJ，KimBW，KoMG，etal.Modifiedmodalmethodsforcalculatingeigenpairsensitivityofasymmetricdampedsystem[J].InternationalJournalforNumericalMethodsinEngineering，2004，60:1847-1860.

[8]LiL，HuYJ，WangXL.Aparallelwayforcomputingeigenvectorsensitivityofasymmetricdampedsystemswithdistinctandrepeatedeigenvalues[J].MechanicalSystemsandSignalProcessing，2012，30:61-77.

[9]ZhangDW，WeiFS.Dynamicflexibilitymethodwithhybridshiftingfrequencyforeigenvectorderivativeswithconcentratedeigenvalues[J].AIAAJournal，2002，40(10)：2047-2052.

[10]XieHQ.IRAM-basedmethodforeigenpairsandtheirderivativesoflargematrix-valuedfunctions[J].NumericalLinearAlgebrawithApplications，2011，18:513-538.

[11] 张淼，于澜，鞠伟.模态跳跃现象对振动分析的影响研究[J].合肥工业大学学报：自然科学版，2015，38(11)：1524-1529.

[12] 张淼，于澜，鞠伟.亏损振系广义状态向量灵敏度的移频算法[J].计算力学学报，2013，30(6)：872-878.

[13] 张淼，于澜，鞠伟.复模态正交性理论的异常现象及对策分析[J].应用数学和力学，2014，35(10)：1081-1091.

The Research on Method for Eigen-curve of Complex Modal Parameter and Its Application

YU Lan，et al.

(SchoolofScience，ChangchunInstituteofTechnology，Changchun130012，China)

The method for eigen-curves of complex modal parameters is presented in this article.Several graphs are drawn，such as curve of complex frequency，curve of complex mode and curve of the first-order sensitivity of complex mode by using the numerical technique at more nodes.The analysis to the representative eigen-curves of complex modal parameters can not only optimize and control structure but also examine the accuracy of sensitivity.A truck integrated structural system with 7 degrees of freedom is used to demonstrate the effectiveness and feasibility of this method.

complex modal parameter；sensitivity；eigen-curve；Spline interpolation

10.3969/j.issn.1009-8984.2017.01.027

2016-11-21

吉林省科技发展计划项目(20160101342JC) 吉林省教育厅“十三五”科学技术研究项目(2016302)

于澜(1971-)，女(汉)，吉林永吉，硕士，副教授 主要研究计算力学与结构优化设计。

O32

A

1009-8984(2017)01-0113-06