四平市城区地下水水质评价

秦 雨，王兆波，杨焕欣

(1.长春工程学院水利与环境工程院，长春 130012； 2.吉林省水工程安全与灾害防治工程实验室，长春 130012； 3.长春工程学院理学院，长春 130012)

四平市城区地下水水质评价

秦 雨1,2，王兆波1,2，杨焕欣3

(1.长春工程学院水利与环境工程院，长春 130012； 2.吉林省水工程安全与灾害防治工程实验室，长春 130012； 3.长春工程学院理学院，长春 130012)

在四平市2012年城区地下水水质监测数据的基础上，利用改进的内梅罗指数法模糊综合评判法对研究区的地下水进行了水质现状评价。评价结果显示，改进的内梅罗指数法削弱了最大值评价指标在最终评价等级中的贡献，使得评价等级“居中”(占90%)；而模糊综合评判法由于“相乘取大”的运算法则使得权重矩阵A和隶属度矩阵R都与指标的质量浓度相关，夸大了超标指标在最终水质评价等级中的贡献，导致评价等级多为Ⅰ类和Ⅴ类水(占60%)。结合地下水水质监测数据，认为改进的内梅罗指数法更贴近真实地下水水质情况，也说明了任何的水质评价都不能脱离监测数据而只依赖数学的计算方法进行。

地下水；水质评价；改进的内梅罗指数法；模糊综合评判法

1 研究区概况

四平市区位于市境南部，东南部至西南部与辽宁省为邻。市区面积1 080 km2，辖铁东区和铁西区，2个乡和3个镇，市区人口63万人[1]，地下水资源量6.174×107m3[2]。市区地处松辽平原腹地与长白山余脉低山丘陵地带，东高西低。按地形分区划分，东南部为低山丘陵区，面积804 km2；中西部为松辽平原区，面积276 km2。辖区内主要的地表水体有条子河、下山台水库和山门水库。四平市土质肥沃，草原辽阔，是国家重点商品粮基地，素有“松辽平原黄金玉米带”之称，也是吉林省最的重要交通枢纽之一。

2 地下水水质评价方法

水质评价是对区域内的水环境要素进行综合分析，对水质优劣进行定量评价，来判断该地下水等级的过程。水质评价是确保水质安全、合理利用水资源的前提。自20世纪60年代Horton等人提出水库质量评价的水质指标概念以来，国内外对水质评价指标的选取和评价的方法开展了一系列的重要研究。

美国是较早开展水质评价的国家。1965年，Horton提出将质量指标法用于水质评价；接着Brownd提出了水质质量指数(WQI)；Nemerow提出了内梅罗法；Ross提出了利用生化需氧量、氨氮、悬浮物及溶解氧4 项指标评价水质[3-7]。目前，水质评价不仅考虑物理和化学指标，还考虑生物指标，使水质现状评价更加全面、科学。我国的水环境质量评价工作开始于1973年，大体上经过了4个阶段：初步尝试阶段、广泛探索阶段、全面发展阶段和环境影响评价阶段。

国内外的大量讨论综合水质评价方法的文献中，目前已有几十种评价方法，现行的典型水质评价方法主要有单因子评价法、模糊综合评价法、灰色系统评价法、BP人工神经网络评价法、主成分分析法、层次分析法等。已颁布的GB/T 14848—93《地下水质量标准》中根据地下水的不同用途把地下水质分为了5个等级。目前常用的水质评价方法有F值法、内梅罗指数法和模糊综合评价法[8]。

3 地下水水质现状评价

本次选取四平市城区具有代表性的潜水监测井2012年实测数据进行水质评价，数据来源于四平市水文局。

3.1 改进的内梅罗指数法

内梅罗指数法在计算式中含有评价参数中的最大分指数项，可以突出质量浓度最大的水质指标对环境质量的影响和作用。近年来，为克服传统的内梅罗指数过于突出最大污染因子对水质影响和未考虑权重因素的特点，有学者[9]提出采用改进的内梅罗指数计算公式代替典型的内梅罗指数计算公式：

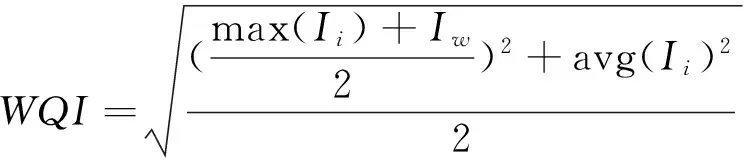
(1)

式中：WQI为综合污染指数；max(Ii)为n项水质指数的最大值；Iw为权重最大的某项水质指标的污染指数；

avg(Ii)为n项水质指标污染指数的算数平均值。

本文采用GB/T14848—93《中华人民共和国地下水质量国家标准》，将地下水按水质划分为5类。各项指标按照其在地下水中的含量划分为5类，评价时需先进行各单项组分评价，划分所属质量类别，不同类别标准值相同时，从优不从劣。本次地下水水质评价主要选取氨氮、硝酸盐氮、亚硝酸盐氮、氟离子、高锰酸盐指数、总硬度、矿化度等15个指标为评价因子进行评价。改进的内梅罗指数法进行水质评价的评价结果详见表1。

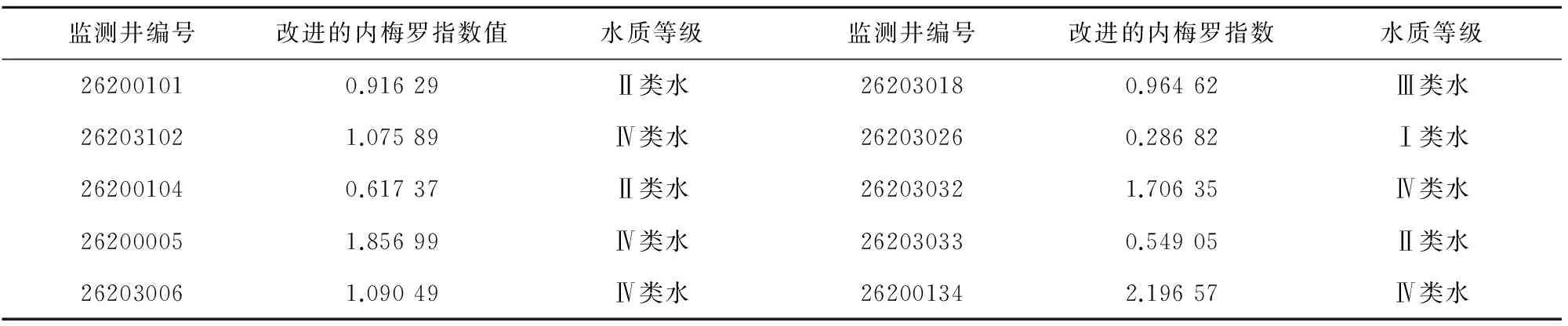
表1 改进的内梅罗指数法水质评价成果表

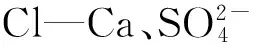
3.2 模糊综合评判法

在水质的定性和定量评价中，广泛存在着随机性和模糊性，如评价参数的性质、参数的时间变化、污染程度和污染分区界限的确定等，都是典型的模糊问题。模糊数学应用于地下水质量评价，是通过函数关系把地下水质指标的监测值转化为水质质量优劣程度的质量值。它克服了“非此即彼”的分类的不合理性，提出了以隶属度为原则进行分类的方法，这一方法更强调事物对某范畴的“亦此亦彼”的客观存在的“中间过渡的不分明性”，即模糊性。

模糊综合评判法建立在比较严谨的数学模型基础上，通过综合评价值的计算以及模糊级别判断，可以较直观地判断水质优劣，并从总体上判断地下水所属质量等级。是目前在水质评价中应用最为广泛的模糊数学评价方法[10-11]，其计算公式为：

B=AR，

(2)

式中：B为综合评判结果，表示评价样本对评判分类的隶属度；A为参与评价指标的权重向量，一般通过超标倍数归一化得到；R为各评价指标与评价标准之间的模糊关系矩阵，由定义的隶属函数确定。

3.2.1 确定评价因子及评价标准

同样选取氨氮、硝酸盐氮、亚硝酸盐氮、氟离子、砷、汞、铬、氰化物、挥发性酚、高锰酸盐指数等15个指标为评价因子，以国家GB/TL14848—93《地下水质量标准》为评价标准进行四平市地下水水质评价。

3.2.2 确定因子权重矩阵

地下水环境受到多因子共同影响时，考虑到每项指标对地下水环境的影响程度不同，在水质质量中的作用大小不一，需要求其权重，计算方法可用“超标倍数归一法”。计算公式如下：

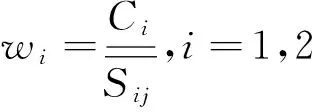
(3)

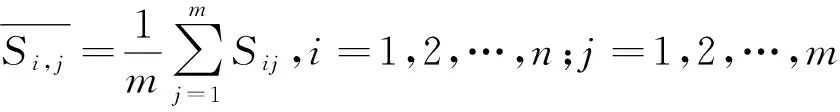
(4)

式中：wi为第i项水质指标的权重；Ci为第i项水质指标的实测质量浓度；Si,j为第i项指标第j类水的质量浓度限值。

在计算求得权重的基础上，对权重进行归一化处理，以求得权重向量。计算公式为：

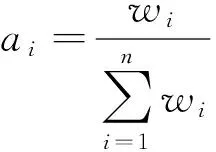
(5)

3.2.3 确定模糊关系矩阵

地下水水质类别分为5类，即Ⅰ级、Ⅱ级、Ⅲ级、Ⅳ级、Ⅴ级。

当第i项水质指标实测质量浓度为Ⅰ类水质时，其对应的隶属函数为

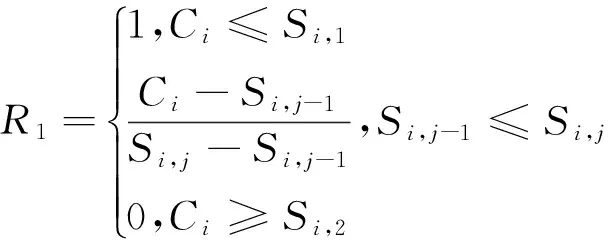
当第i项水质指标实测质量浓度为第j类水时(Ⅱ≤j≤Ⅳ)，其对应的隶属函数为

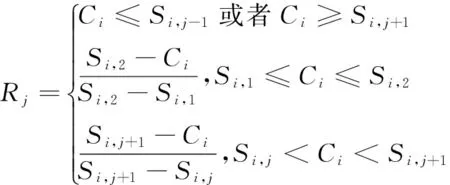
当第i项水质指标实测质量浓度为Ⅴ类或劣Ⅴ类水时，其对应的隶属函数为

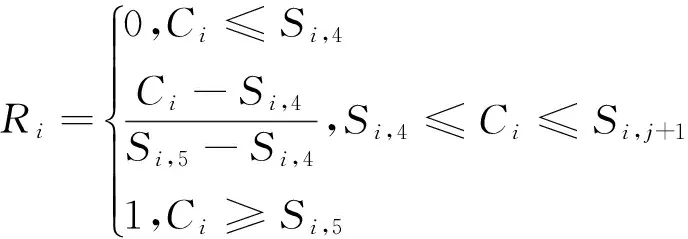
式中：μj为水质指标实测质量浓度对j类水的隶属度；Ci为水质指标i的实测质量浓度值；Si,j为水质指标i第j类水的浓度限值。

将各个评价因子对各水质等级的隶属度作为行向量就可以形成模糊关系矩阵R。以监测井26200101为例，其隶属度矩阵R为

以本论文中1号监测井(26200101)为例，计算各评价指标归一化后的权重向量A为

A=(0.00 0.00 0.00 0.00 0.21 0.08 0.00 0.01 0.01 0.00 0.00 0.07 0.14 0.17 0.31)

隶属度B为：B=AR=(0.432 0.402 0.166 0 0)

根据“相乘取大”的原则，可以最终判定该监测井综合水质为Ⅰ类。以此类推，可得出其他观测井的水质评价结果。

3.2.4 评价结果

采用模糊综合评判法对四平城区地下水水质评价结果详见表2。

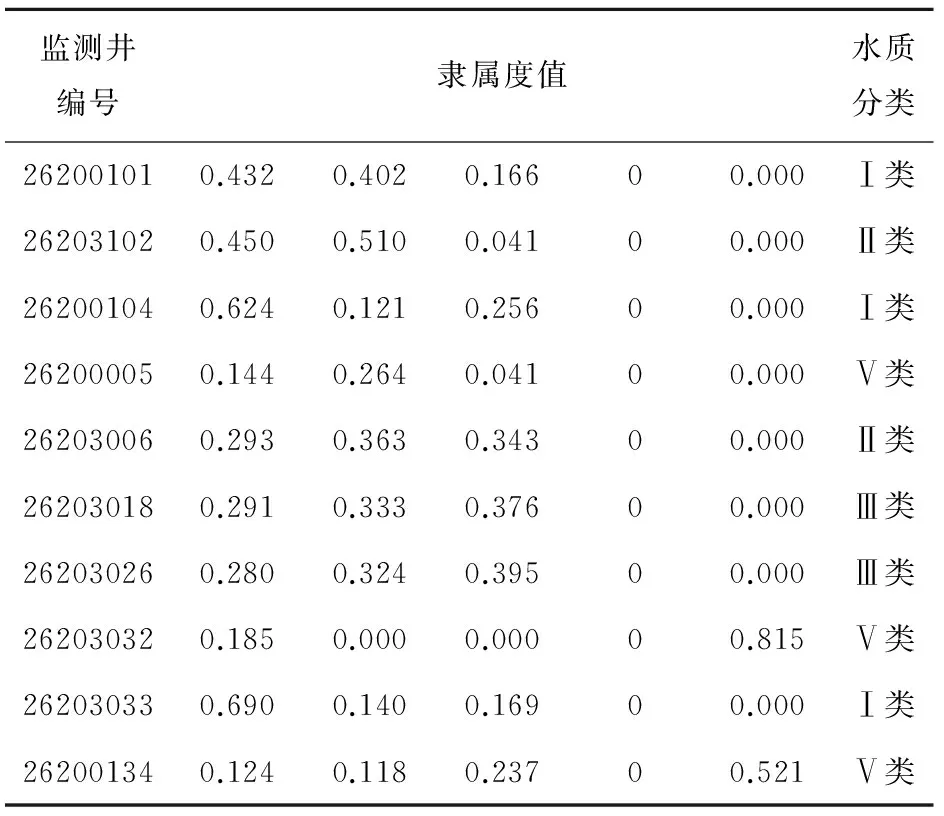
表2 模糊综合评判法水质评价成果表

水质评价结果显示，运用模糊综合评判法确定的水质等级集中在Ⅰ类和Ⅴ类的两个极端等级，占评价监测井的60%，即采用模糊综合评判法确定的水质等级出现或极优或极差的两极分化情况。结合本文评价水质监测井的监测数据，利用模糊综合评判法评价为Ⅴ类水的3个监测孔(26200005、26203032、26200134)利用改进的内梅罗指数法均评价为Ⅳ类水，利用模糊综合评判法评价为Ⅰ类水的3个监测孔(26200101、26200104、26203033)利用改进的内梅罗指数法均评价为Ⅱ类水。分析出现这种情况的原因是模糊综合评判法的“相乘取大”原则在运算中的权重矩阵A和隶属度矩阵R都与指标的质量浓度相关，做相乘运算后实际上是与指标的质量浓度平方相关，因此夸大了超标指标在最终水质评价等级中的贡献。而改进的内梅罗指数法考虑了参评评价因子项目和数目的差异，从而降低了最大评价因子在评价结果中的贡献，使得评价结果较“居中”，未出现模糊综合评价法“两极分化”的评价结果。

4 结语

运用改进的内梅罗指数法对研究区地下水现状评价，其结果显示四平城区地下水多为Ⅱ-Ⅳ类水(占90%)；而运用模糊综合评判法对研究区地下水现状评价，其结果显示四平城区地下水多为Ⅰ类和Ⅴ类水(占60%)。

综上所述，笔者认为采用改进的内梅罗指数法对四平城区地下水水质进行评价的评价结果更符合实际情况，也与文献报道的结论相一致[12]。此外，可采用“相乘相加”、“取小相加”等其他隶属度函数的复合运算方法改进模糊综合评判法进行水质评价，并结合水质监测数据进行进一步分析，从而确定地下水水质等级。这也说明，任何水体的水质评价都不能够脱离基础的监测数据，而单单依靠数学的计算方法来进行。

[1] 高世毅.四平市地下水资源管理现状评价研究[J].水科学与工程技术,2015(4):4-7.

[2] 张骄阳，梁雨华.吉林省四平市饮水水源现状及保护对策研究[J].旅游纵览(下半月),2014(6):253-254.

[3] Odada Eric O，Olago Daniel O,Bugenyi Fred,et al.Environmental assessment of the East African Rift Valley lakes [J].Aquatic Sciences-Research across Boundaries,2002,65(3):254-271.

[4] Bhuyan S J,Koelliker,Marzen L J,et al.An integrated approach for water quality assessment of a kansas watershed [J].Environmental Modelling and Software,2003,18(5):473-484.

[5] Neelakantan T R,Pundarikanthan N V.Neural network-based simulation-optimization model for reservoir operation [J].Journal of Water Resource Planning and Management,2000,126(2):57-64.

[6] Xue Ming.A novel water quality assessment method based on combination BP neural network model and fuzzy system [J].Journal of Computers,2013,8(6)：1587-1593.

[7] Wan Jun,Bu Hongmei,Zhang Yuan,et al.Classification of rivers based on water quality assessment using factor analysis in Taizi River basin,northeast China[J].Environmental Earth Sciences,2013,69(3)：909-919.

[8] 张晓叶，张永祥，任仲宇，等.不同地下水水质评价方法的比较及实例应用[J].水资源与水工程学报,2014(4):98-101.

[9] 关云鹏.利用内梅罗指数法模型评价地下水水质的探讨[J].山西水利科技,2012(1):81-84.

[10] 尹静章，傅静，谢营，等.改进的模糊数学评价法在德州市地下水水质评价中的应用[J].治淮，2010(12)：22-25.

[11] 寇文杰.修正的模糊综合评判法在地下水水质评价中的应用[J].南水北调与水利科技,2013(4):71-75.

[12] 房春生，孟赫，单玉书，等.基于GIS 的吉林省地下水水质模糊评价[J].吉林大学学报(地球科学版),2011(9):293-297.

The Groundwater Quality Evaluation for Siping Urban Area in China

QIN-Yu，et al.

(SchoolofWaterConservancy&EnvironmentEngineering,ChangchunInstituteofTechnology，Changchun130021，China)

Based on the monitor data of groundwater quality in Siping China，this paper evaluates the groundwater quality by the improved Nemerow index method and the puzzle comprehensive evaluation.The evaluation result shows that the improved Nemerow index method decreases the contribution of the max evaluation index in the final groundwater quality level，which leads the quality to the “middle” level(90%)，while the puzzle comprehensive evaluation builds up the contribution of over index in final groundwater quality evaluation for the “multiplication take the big” the algorithm which correlates the concentration with both the weight matrixAand the membership matrixR，with the result in the quality of Ⅰ and Ⅴ level (60%).Combining with the monitor data of groundwater quality，the paper concludes that the evaluation by the improved Nemerow index method is more real to the real groundwater quality，and any water quality evaluation can’t be evaluated only by mathematics calculation without the monitor data.

groundwater；water quality evaluation；improved Nemerow index method；puzzle comprehensive evaluation

10.3969/j.issn.1009-8984.2017.01.018

2016-10-09

长春工程学院校青年基金(320140011) 吉林省发改委项目(2013G049)

秦雨(1982-)，女(汉)，黑龙江齐齐哈尔，博士，讲师 主要研究水文学及水资源。

TV211.12

A

1009-8984(2017)01-0071-04