由机械能守恒给出第二类Lagrange方程的探究
马天麒赵靖宇
(清华大学航天航空学院,北京100084)
由机械能守恒给出第二类Lagrange方程的探究
马天麒1)马天麒,清华大学航天航空学院钱学森力学班2015级学生.E-mail:matq15@mails.tsinghua.edu.cn赵靖宇2)赵靖宇,清华大学航天航空学院钱学森力学班2015级学生.E-mail:zhaojing15@mails.tsinghua.edu.cn
(清华大学航天航空学院,北京100084)
保守系统的运动微分方程,可以使用第二类Lagrange方程列写,从Langrage方程也可以推导出保守系统的机械能守恒.有老师提到,曾有学生在作业中用机械能守恒给出正确的Lagrange方程.本文探讨这种做法的可行性,并针对某些特殊情况给出了由机械能守恒得到Lagrange方程的具体步骤.
机械能守恒,第二类Lagrange方程,保守系统
1 问题的导入
以椭圆摆为例,来说明本文研究的求Lagrange方程的方法.如图1所示,取两物块质量分别为m1和m2,物块1的位移为x,摆与竖直方向的夹角为θ.摆的长度为l,质量不计,则

由Lagrange方程可以很容易地求得系统的运动微分方程


图1
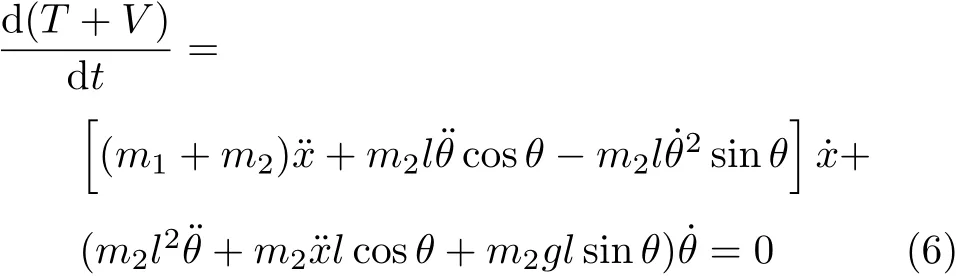
这种方法究竟是否具有普适的正确性?操作步骤又该是什么样的?本文将从Lagrange方程出发,试着探讨在什么情况下,用这种“能量求导”的方法,可以得到正确的微分方程,并具体讨论了从能量守恒得到Lagrange方程的方法.
2 由机械能守恒给出Lagrange方程的方法
对于保守系统,机械能是一个守恒量,即E= T+V=const.且由于保守系统的约束必是理想、完整、定常的,则有
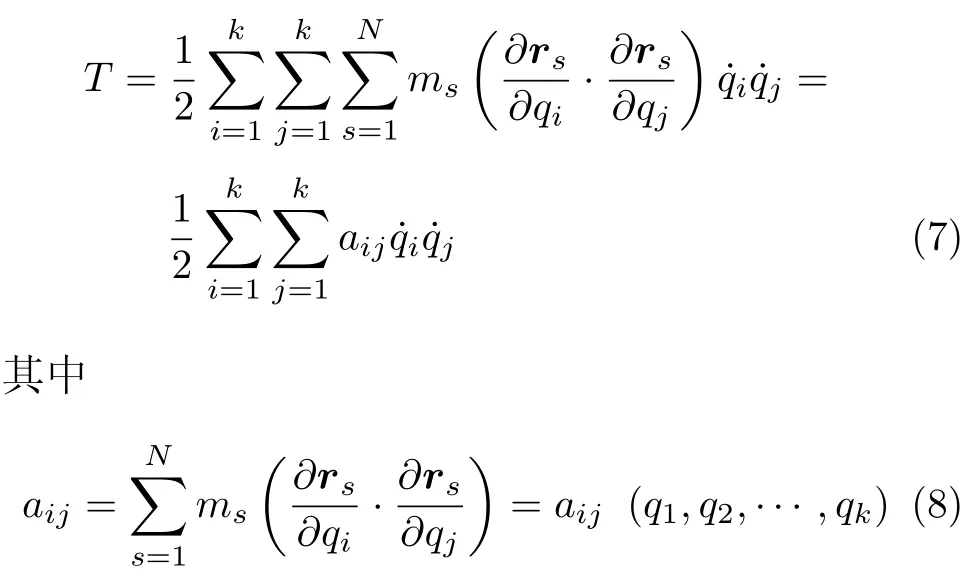
即aij是关于广义坐标q1,q2,···,qk的函数,且观察表达式可得aij=aji.此时Lagrange方程可以写为
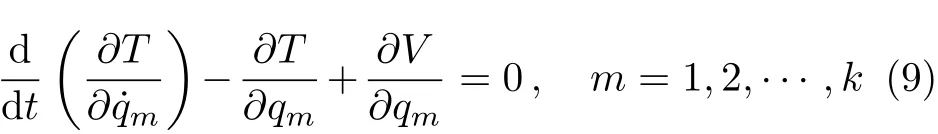
现将式(7)代入式(9)得

接下来再来看机械能守恒,即


事实上,由分析力学知识可知,在推导广义能量守恒时已经运用过上面的方法,所以由式(10)可以很容易地推得式(11),即这种方法从理论上讲是可以实现的.现在的问题是如何从式(11)反推出式(10),可以看出式(11)中

这2k2+k项,恰好是式(10)中
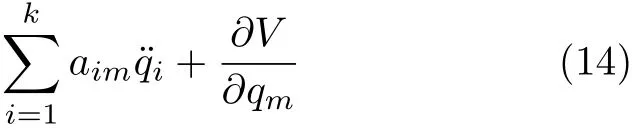
3 方法的可行性
在由式(10)和式(11)推导式(12)时可以发现,求和之前的2k3个含广义坐标一阶导数交叉乘积的项通过求和后得到的2k3项,将会通过合并同类项变成k3项,因此当反向进行上述过程,即从机械能守恒推导Lagrange方程时,就可能需要人为地将某些已经合并过的项拆分出来,但是这在一般情况下是不容易做到的.接下来对一些比较简单的特殊情况做一些讨论.
3.1 不含交叉项的情况
由于主要难度出现在广义速度的交叉项上,因此只要想办法在机械能守恒中不出现交叉项,就一定能够保证可以直接拆分,即要求

在此条件下,由机械能守恒得到Lagrange方程的步骤概括如下:
(1)确定广义坐标qi(i=1,2,···,k),并列写系统机械能E;
(2)求E对时间的导数;
3.2 弱耦合情况
3.1 节中对aij的要求是比较高的,一般情况下较难达到,所以将上述要求放宽,即要求aij满足
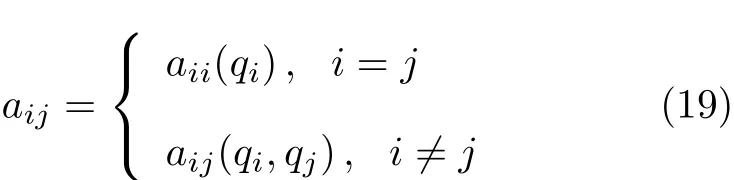
即动能中的每项系数只与它所关联的两个广义坐标有关.此时,式(10)和式(11)分别可以化为
研究表明,高血压患者的QRS-T夹角大于正常人群。Dern等[17]发现在高血压治疗过程中,高血压人群的QRS-T夹角随着血压的降低而减小,因此认为QRS-T夹角的变化可能与心肌缺血及心肌肥厚有关。Atsma等[18]在969名不伴有左室肥厚的绝经后妇女中发现,血压的升高与QRS-T夹角增大相关,并提出在发生左室肥厚前,血压升高可导致心室去极化和复极化异常。至于能否在临床上应用QRS-T夹角来评价高血压治疗效果,仍需进一步的研究证实。

对比可以发现,上下两个方程同样具有相似的形式,只需令˙qm的系数分别等于0,同样可以得到系统运动的微分方程.并且注意到,在上式中将˙qm提出后,只有广义速度的平方项,而没有交叉项,所以可以较容易地写出.此时由机械能守恒得到Lagrange方程的步骤概括如下:
(1)确定广义坐标qi(i=1,2,···,k),并列写系统机械能E;
(2)求E对时间的导数;
容易看出,引言中的椭圆摆问题的解答就是这样做的.
3.3 一般情况
为了方便进行重组,将动能对时间的导数写成下面的形式

那么,可以证明

即为系统的第m个运动微分方程.事实上,对比式(10)与式(11)可以很容易验证上述结论成立.
现在用一个简单的问题验证上述方法.
研究一个质量为m质点的二维运动,质点在xOy平面内运动,且xOy平面为铅垂面,y轴指向正上方,质点只受重力作用.如果选取直角坐标,则为第1小节中的情况.为了说明本小节中的情况,我们现在选取极坐标研究些问题,则有

显然,此时的动能不满足上述两种特殊情况的

容易验证上述两个方程是正确的.如果仍直接套用第1小节的方法,无法得到正确的结果.
综上,进行上述拆分后,仍可以在保守系统下得到系统运动的微分方程,但是运算已经十分繁琐.然而,通过之前的分析可以知道,采用这种方法只需要算出k3个广义速度的交叉项,相比之下Lagrange方程共需要计算2k3个广义速度的交叉项.所以采用本方法会减少运算量.
4 结论
本文研究了理想完整定常约束下的保守系统中机械能守恒和Lagrange方程的关系,并就某些特殊情况给出了由机械能守恒得到Lagrange方程的具体步骤.需要指出的是,本文所论证和给出的方法仅是求Lagrange方程的一个小技巧,在某些简单情况下确实可以用,可以帮助我们理解为什么有些同学用错误的方法“将错就错”得到了正确的Lagrange方程.
(责任编辑:胡漫)
O31
A
10.6052/1000-0879-16-414
2016–12–20收到第1稿,2017–01–03收到修改稿.
马天麒,赵靖宇.由机械能守恒给出第二类Lagrange方程的探究.力学与实践,2017,39(2):214-217,174 Ma Tianqi,Zhao Jingyu.Derivation of Lagrange equation from the law of conservation of mechanical energy.Mechanics in Engineering,2017,39(2):214-217,174

