旋转单元电场矢量法的真解判定方法

卫旭芳

（中国空空导弹研究院，河南洛阳471009）

旋转单元电场矢量法的真解判定方法

卫旭芳

（中国空空导弹研究院，河南洛阳471009）

旋转矢量法可被用来进行有源相控阵列的通道校准。每轮测试后在计算相应通道的幅相时会出现伪解。通过调整固定场矢量的幅度，进行两轮测试，判定两轮测试中绝对解不变的那组解为真解。其辨别方法，在有效判定真解的同时，也降低了计算量与测试量。另外，由于两轮测试时只需测量幅度信息，降低了测试设备复杂度。数值仿真结果证明了此方法的有效性。

旋转单元电场矢量法，校准，真解辨别

0 引言

有源相控阵列阵元通道不一致会导致通道幅相误差的存在，会带来指向精度变差，副瓣抬升等恶劣影响，因此，需要对阵元通道进行一致性校正。旋转单元电场矢量法（REV，Rotating-element Electric-field Vector），是日本学者Seji Mano和Takashi Katagi提出的有源相控阵列通道校准方法［1-2］。该方法的特点是不需要任何的相位测量，而仅仅依靠功率测量然后通过数学计算就可以确定各个单元的初始电场参数。具体实施时，通过软件控制阵列单元前端的移相器，当单个阵元相移值改变时，测量合成电场矢量电场强度的变化，并记录其测量最大功率、最小功率和相应的相差，最后将测试结果进行数学处理，便可得到该阵元的幅度和相位值。由于只需要测量功率信息，因而设备量和校正复杂度大大减小，并且该方法在测量时将阵元之间的互耦也考虑在内，因此，工程实际中该方法获得了广泛应用［3-5］。

但是REV方法求解时会得到两组解，为了判定出真解，文献［1］给出了3种方法，文献［6］对文献［1］中的方法进行比较分析，指出其优点和不足，同时给出了一种有效消除解的二义性的方法。本文对上述方法进行研究，根据真解伪解的物理意义，判定两次测试中绝对解维持不变的那组为真解。本文使用的真解辨别方法，相比文献［6］降低了计算量与测试量，由于两轮测试均只需测量幅度信息，因此，在测试设备和场地受限的情况下也适用。

1 REV法简介与其解的二义性

当一个单元的移相器相移改变时，该单元的矢量以类似于圆半径的形式旋转，合成电场矢量端点位置落在这个圆上，如图1所示。

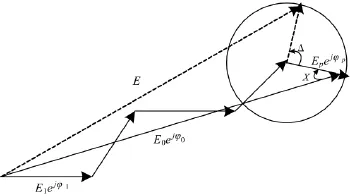
图1 旋转矢量法原理图

设所有天线单元的合成场矢量的初始幅度和相位记为E0和φ0，其中第p个天线单元的幅度和相位记为Ep和φp，当调整第p个天线单元的移相器使其相位变化为Δ，此时对应的合成场矢量可以表示为:

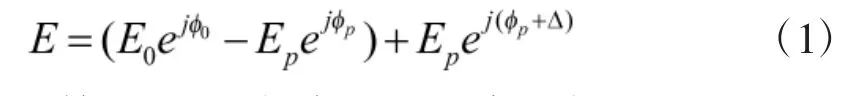
定义第p个天线单元相对合成场矢量的相对幅度和相对相位定义为:

由式（4）可知，复功率系数Q随着单元相位移动而变化，且变化规律符合余弦函数的形式。定义Q的最大值和最小值的比值如下:

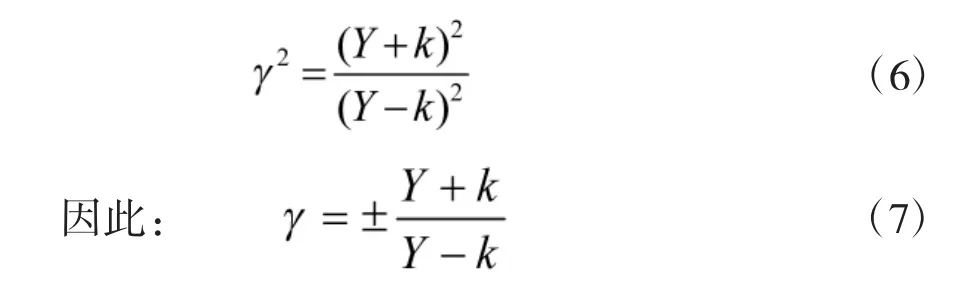
定义

那么可以得到如下两组解:

当γ=（Y+k）/（Y-k）时:

由式（4）、式（5）可以看出，通过调整第p个阵元的相位，并同时测量整个阵列的功率，可得到功率最大时对应的相位变化-Δ0，最大功率和最小功率的比值γ2，再利用式（9）、式（10）可计算出相对幅度和相对相位。若已知k＜Y，判定第1组解为真。若已知k＞Y，判定第2组解为真［1，3］。由于未知k和Y的大小关系，所以需要判定真解的方法。可以证明两组解中一组解为移相阵元场矢量的相对幅相，另一组解则为除移相阵元以外的其他阵元的合成场矢量的相对幅相［6］。

2 真解的判定方法

文献［1］给出了几种判定真解的方法:

①对于每个待测阵元，调整阵列其阵元通道移相器相位，使得条件k＜Y满足再进行矢量旋转功率测试，这种情况下第1组解始终就是真解。

②调整待测阵元的移相器从0°变化到360°，在测量阵列合成功率的同时，加入对阵列合成相位的测量，并监测阵列合成相位变化范围，若合成相位变化小于180°，对应于k＜Y的情形，选择第1组解作为真解；若合成相位变化大于180°，对应于k＞Y的情形，选择第2组解作为真解。

③对于待测初始幅相阵元，分别针对两种不同的初相分布，进行两次旋转矢量测试，真解是两次测试中维持不变（remain identical）的那组解。

第①种方法在测量之前要加入校正，比较复杂，且只适用于阵列中各个阵元的初始场矢量幅值相差不大的情况，因为当其中某个阵元的初始场矢量幅值远远大于其他阵元的幅值时，无论怎么调整其他阵元移相器相位也无法满足k＜Y的条件［1］，如图2所示。第②种方法虽然思路清晰，但是由于要进行相位测量，增加了测量的复杂性，在测试场地和测试设备受限的情况下无法实现。

图2 初始场矢量过大示意图

文献［6］对上述真解辨别方法进行分析，并指出第③种方法存在描述有误的状况:根据式（9）、式（10）求出的k和X实际上是待测单元初始场矢量相对初始总场的相对幅度和相对相位，由于两轮测试而言初始相位分布不同，初始总场也就不同，两轮测试得到的真解也不同，因此，不存在“不变的解”。并针对第③种方法提出了解决方案:对求解量进行变换，分别设置多组不同的初始相位分布，进行多轮旋转矢量测试，最终消除解的二义性。但是这种方法增大了计算量和测试量，每轮测试都需要计算4组解，有可能需要3轮或者更多轮的测试。本文基于以上讨论，在真解伪解的物理意义的基础上，采用如下的真解判定方法:对于待测阵元，分别针对两种不同的初始相位分布，进行两次旋转矢量测试，真解是两次测试中幅度或相位的绝对解维持不变的那组。注意，相比于原有方法，这里维持不变的意思指的是求出的幅度和相位的绝对解维持不变，因此，要测量所有阵元合成场矢量的幅相，最后利用算出的相对解和式（1）求出绝对解。若观测量是幅度，其示意图如图3所示，具体实施过程见第4部分。同理，若观测量是相位，其示意图如图4所示，具体实施过程不再详述。

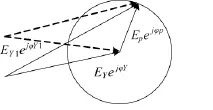
图3 改变固定场矢量幅度

图4 改变旋转矢量相位

3 实施过程

采用改变初始相位使两次测量的固定矢量的幅度改变时，详细描述如下几步:

第1步，测量所有阵元的合成幅度，然后对待测阵元（记为第p阵元），进行旋转矢量测试，并依据式（9）、式（10）计算出相对幅度和相对相位，结合合成幅度，可以得到该待测阵元p的两组绝对幅度，记为Ep1=［Ep1（1），Ep1（2）］；

第2步，调整除待测第p阵元外的其余阵元的初始相位，测量所有阵元的合成幅度，然后对待测阵元，进行第2次旋转矢量测试，同样依据式（9）、式（10）计算出的相对幅度和相对相位，结合合成幅度，可以得到该待测阵元p的两组绝对幅度，记为Ep2=［Ep2（1），Ep2（2）］；

第3步，比较Ep1（1），Ep1（2），Ep2（1），Ep2（2），其中维持不变的那个解就是真解。

示意图如图4所示，两次测试待测阵元p的初始场向量Epejφp均不变，通过调整其他阵元相位使得固定场矢量的场强由EYejφY变为EY1ejφY1，如图4虚线所示，由于旋转矢量初始值没有变动，因此，在后面的REV测试中求得的其绝对幅度也不会变化，幅度绝对解不变的就是真解，幅度绝对解变化的就是固定场矢量的解即伪解。

4 真解判定数值实例

仿真采用8阵元直线阵列，各个阵元间距半波长，数字移相器衰减器的位数均为6位，数字移相器移相范围为0～2π，相位误差服从均值为0、标准差为80°的高斯分布；数字衰减器幅度误差服从均值为0、标准差为1 dB的高斯分布［7-9］。首先设定k和Y的大小关系，分如下3种情况，分别记为条件1、2、3:①第1阵元k＞Y，其余阵元k＜Y；②第2阵元k＞Y，其余阵元k＜Y；③所有阵元都满足k＜Y。

仿真是在未知k和Y相对大小关系情况下进行的。采用本文提出的方法记为方法④判定真解。第1次测试时所有阵元都采用初相，旋转第p阵元的相位进行测试。第2次测试时使得除了第p阵元外的其余阵元的相位发生随机改变，这样两次测试过程中固定场矢量的绝对幅度是会发生改变的，而对于第p阵元（待测阵元），其两次测试的幅度是保持不变的。

表1～表3分别对应于条件1～3下的数值仿真结果。幅度1_1、幅度1_2表示第1轮测试第1组解、第2组解；幅度2_1、幅度2_2表示第2轮测试第1组解、第2组解。可以看到3种条件下判定出的结果和初始设定条件一致。条件3校正前后的阵列增益图见下页图5。可见校正后的阵列增益逼近理想情况（无通道误差）下阵列增益。本文方法在两次测试时都无需测量相位。因此，可降低对测试设备和测试场地的要求。

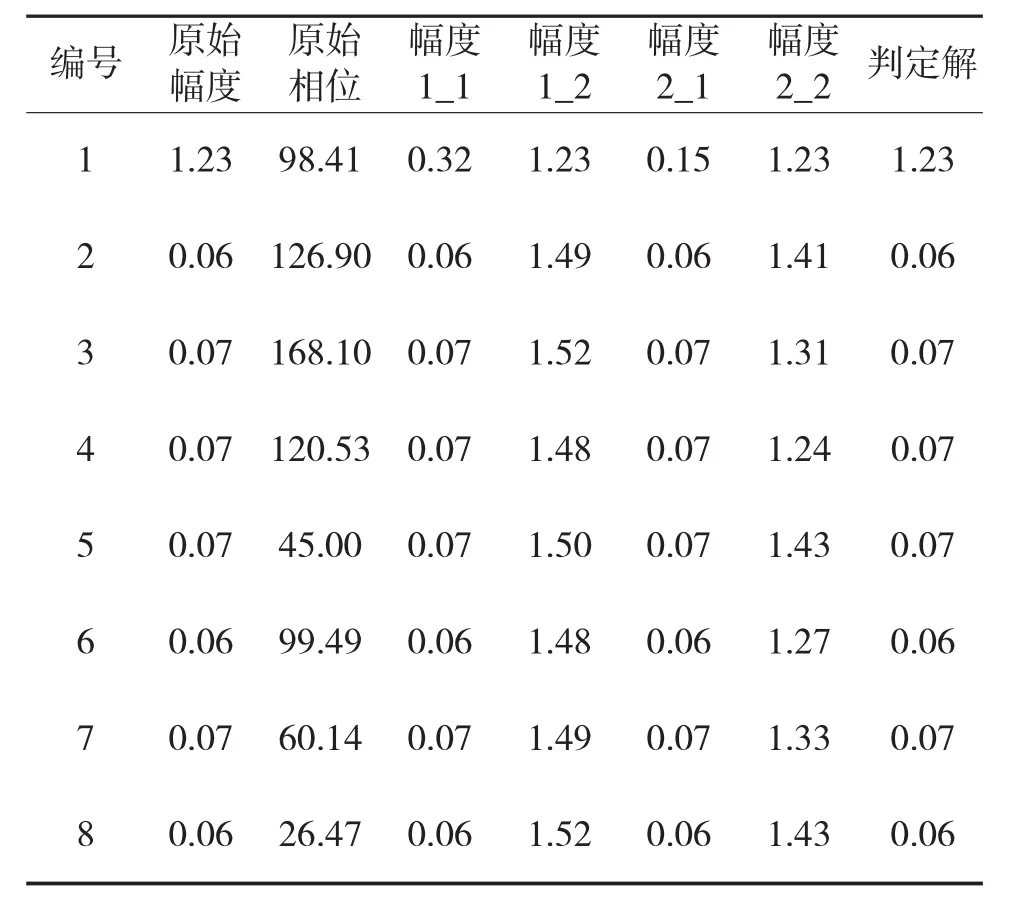
表1 条件1数值仿真结果（方法4）

表2 条件2数值仿真结果（方法4）

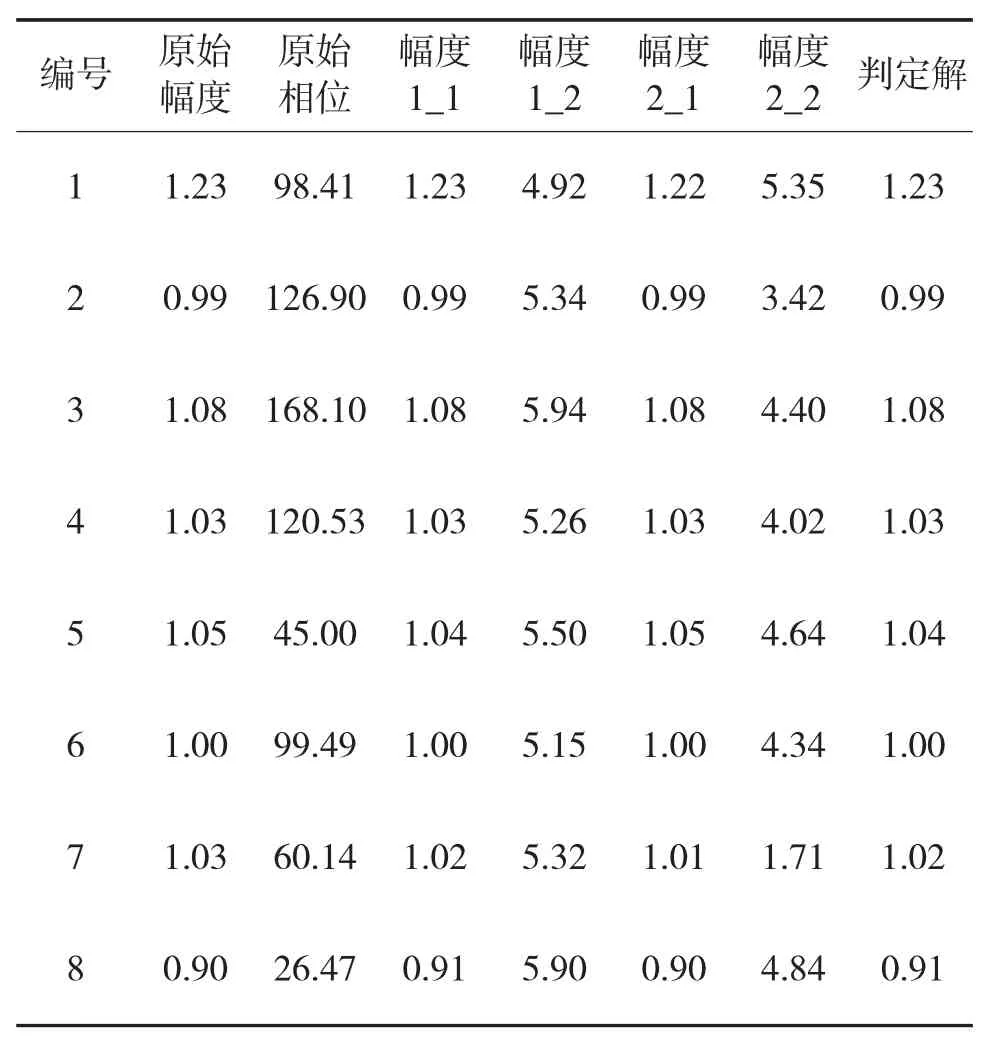
表3 条件3数值仿真结果（方法4）

图5 条件3幅度解与校正前后增益比较图

5 结论

当用REV法进行通道校准时，为了辨别真解，规划两轮测试。通过使固定场矢量的幅度发生改变进行两次测试，判定两次测试中幅度绝对解不变的那个是真解。数值仿真结果证明了本文方法的有效性。由于该真解辨别方法避免了相位测量，在测试场地和测试设备受限的场合也适用。

［1］KOJIMA N，SHIRAMATSU K，CHIBA I.Measurement and evaluation techniques for an airborne active phased array antenna［J］.IEEE International Symposium on Phased Array Systems and Technology，1996（10）:231-236.

［2］SEIJI M，TAKASHI K.A method for measuring amplitude and phase of each radating element of a phased array antenna［J］.Electonics and Communication in Japan，1982，65-B（5）:58-61.

［3］樊小景.弹载相控阵天线校正方法研究［D］.北京:中国航空研究院，2011.

［4］刘明罡.5_8GHz通信系统阵列天线设计与校正［D］.北京:清华大学，2008.

［5］刘明罡，冯正和.分组旋转矢量法校正大规模相控阵天线［J］.电波科学学报，2007，22（3）:380-384.

［6］翟禹，苏东林.旋转矢量法解的二义性及其消除方法［J］.北京航空航天大学学报，2012，38（11）:1450-1453.

［7］金荣洪，耿军平，范瑜.无线通信中的智能天线［M］.北京:北京邮电大学出版社，2006:193-200.

［8］MANO S，KATAGI T.A method for measuring amplitude and phase of each radiating element of a phased array［J］.Electronics and Communication in Japan（IEICE），1982，65（5）: 58-64.

［9］张钰.DBF阵列幅相误差校正及其稳健性算法［D］.南京:南京理工大学，2012.

Solution Decision Method for Rotating-element Electric-field Vector in Calibration

WEI Xu-fang
（China Airborne Missile Academy，Luoyang 471009，China）

Rotating-element electric-field vector（REV）method is used for calibration of phased array antenna.The pseudo solution may appear when the amplitude and phase of array channels are calculated.This paper adjusts the amplitude of the fixed electric-field vector by changing the phase of elements to test twice.The true solution is the sets which absolute solution remain identical during the twice test.The method used in this paper reduces the computation and test load.Besides，because the amplitude is needed only，this method has advantage of low requirement for test system.The simulation results verifies the effectiveness of the method used in this paper.

rotating-element electric-field vector，calibration，true solution decision

TN99

A

1002-0640（2017）04-0154-04

2016-03-05

2016-04-28

航空科学基金重点实验室基金资助项目（20140169001）

卫旭芳（1983-），女，河南孟津人，工程师。研究方向：阵列信号处理。