不确定条件下装备器材供应网规划模型*

于双双，王铁宁，李宁，徐胜良

（1.装甲兵工程学院，北京100072；2.解放军78416部队，重庆400054；3.驻618厂军代室，北京100072）

不确定条件下装备器材供应网规划模型*

于双双1，王铁宁1，李宁2，徐胜良3

（1.装甲兵工程学院，北京100072；2.解放军78416部队，重庆400054；3.驻618厂军代室，北京100072）

装备器材供应网是装备器材供应保障工作的重要基石，其规划问题是我军装备器材保障过程的重要战略决策之一。针对节点、边和需求的不确定性，对不确定条件下由多个区域供应子网构成的装备器材供应网的规划问题展开研究。针对问题的特点，用区间分析理论对供应网规划中的不确定性因素进行度量和运算，得到不确定性规划模型，通过区间运算转化，将不确定性模型转化为确定性混合整数规划模型，并设计采用基于禁忌搜索算法的两阶段算法进行求解，分别得到了不同参数设置下的模型求解结果，并将所用算法与模糊规划和随机规划算法的求解结果进行了比较分析。实例分析结果表明所建立的模型和算法具有较强的实用性。

不确定条件，供应网，规划模型，禁忌搜索算法，区间规划

0 引言

装备器材供应网是在上级主管机关统一决策下，以保障装备维修为目的，以统一计划为基础，以一种或多种装备器材为对象，由具有供求关系的装备器材保障单位与装备维修部（分）队需求单位组成的网络。装备器材供应网的规划问题是装备器材供应保障过程中的重要战略决策之一，它为整个装备器材供应保障任务的稳定高效展开奠定了基础。然而由于不确定因素的存在，如节点选择、供应线路、运输环节、需求等的不确定性，导致装备器材供应网规划过程中存在多重不确定性，属于不确定优化问题。尽管已有学者对后勤供应网络［1］、装备保障网络［2-3］、装备维修保障网络［4］进行了研究，但针对不确定性条件下的装备器材供应网的研究还比较欠缺。

早在上世纪50年代，不确定性优化问题就引发了广大学者的研究热情，产生了一系列不确定分析与优化方法，在不确定性决策分析、不确定性信息管理等方面的应用也取得了较大进步，如供应链优化［5］、模块化产品优化设计问题［6］等。近年来，越来越多的学者采用区间数进行不确定性优化分析，并逐渐形成区间规划理论［7］，成为有效解决不确定性优化问题的主要手段之一［8-9］，并在区间型运输规划［10］、资源配置优化［11］、物流网络规划［12］等实际应用中具有较好的表现。鉴于此，结合装备器材供应网的特性及运作实际，采用区间规划理论对不确定条件下的装备器材供应网的规划问题进行研究，构建不确定性装备器材供应网的规划模型，并采用两阶段算法对模型进行求解。

1 不确定需求下装备器材供应网规划模型的构建

1.1 问题描述与模型符号说明

装备器材供应网主要由节点和边构成。供应网的节点分为提供器材的保障节点、具有器材中转功能的连接节点和接收器材的需求点3种类型，保障节点包括工厂、区域配送中心和基层资源点，连接节点包括重要的车站、港口等交通枢纽。供应网中的边主要是各网络节点间的保障与被保障关系以及中转关系，并最终通过运输线路呈现。在待建的供应网中，一般默认各网络节点之间都是连通的，同时任意两个节点之间的线路是两者之间最经济的运输方式，任意两个节点之间最多只能有一条边。

装备器材供应网由多个区域供应子网构成，区域供应子网主要是由区域配送中心、基层资源点和部队需求点构成的供应网络，每个区域内仅设置一个区域配送中心，统筹该区域内的供应保障活动。

为此，首先构建装备器材区域供应子网，最后将各个子网进行边的相互关联即可构成装备器材供应网的整体结构，针对区域配送中心、基层资源点的两级供应保障关系，同时结合网络规划的不确定性进行装备器材供应网的规划设计研究。

设i=1，2，…，I表示器材；j=1，2，…，J表示区域配送中心；k=1，2，…，K表示基层资源点；m=1，2，…，M表示部队需求点；器材、区域配送中心、基层资源点、部队需求点集合分别记为Io，Jo，Ko，Mo，区域配送中心j向基层资源点k供应器材，k向部队需求点m供应器材，此外j也可越级向m供应器材。

模型假设装备器材供应网的节点在一定的备选地域范围内进行设置；候选区域配送中心、基层资源点的位置与数量是已知的；区域配送中心、基层资源点的容量是有限制的；各需求点间的器材需求是相互独立的。

模型所采用的符号如下:

Nim:需求点m对器材i的预估需求量，为区间变量；

Tim:需求点m对器材i的供应时间要求，也为区间变量，本文将其定义为需求点m从提出器材i的需求开始直到需求满足时的间隔时间；

决策变量如下:

yj:0-1变量，yj=1表明在j处设置区域配送中心作为供应网的供应节点，否则yj=0；

yk:0-1变量，yk=1表明在k处设置基层资源点作为供应网的供应节点，否则yk=0；

1.2 装备器材供应网模型的建立

1.2.1 目标函数的确定

装备器材供应网规划过程中的成本主要包括固定成本和运输成本。固定成本主要是区域配送中心、基层资源点的建设和维护成本，即

运输成本包括以下3个部分:器材从区域配送中心经基层资源点供应到需求点的运输成本；器材从基层资源点直接供应到需求点的运输成本；器材从区域配送中心越级供应到需求点的运输成本，即

装备器材供应网的规划目标就是要使总成本最小，则其目标函数为

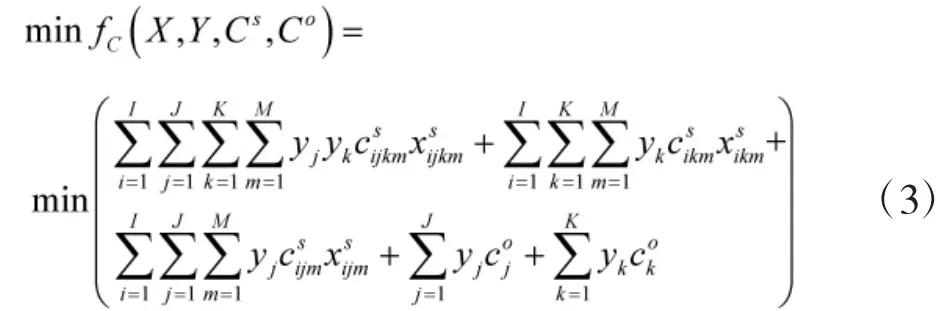
1.2.2 约束条件的确定

模型的约束条件如下:

基层资源点处的器材平衡关系，即基层资源点接收到的器材资源与存储资源总和与从该处转运和直接供应保障的器材资源数量总和保持一致:

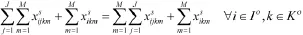
区域配送中心和基层资源点的最大数量约束:

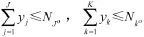
由于不确定性的影响，在满足部队单位器材供应要求时，就不可能100%的满足，但仍要达到一定的器材满足率，即要求部队单位的器材需求满足率必须大于某个置信水平，设ξm表示部队需求点m对于器材i的最小满足率阈值，则有

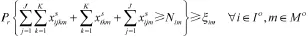
由基层资源点直接供应的及时性限制:

由区域配送中心越级直达供应、层级连续供应的及时性限制分别为:

所有器材供应量决策变量满足非负约束:

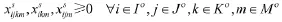
变量为0-1整数变量约束:

1.2.3 模型的确定性转化

①目标函数的确定性转化

首先对区间变量进行区间标度，根据区间运算法则，式（3）可转化为

此外，除区间决策变量外，模型中还存在其他区间参数csikm、csijm、csijkm等，导致最终的决策出现偏差，设为d（fC），满足

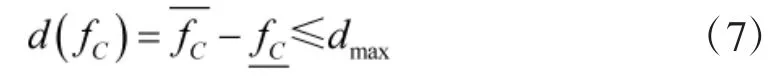
式中，dmax为事先给定的误差控制范围。

定义惩罚因子σ，则式（6）变为

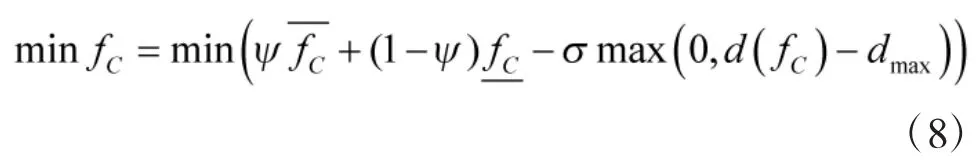
②约束条件的确定性转化

运用区间运算法则，约束条件可转化为s.t.

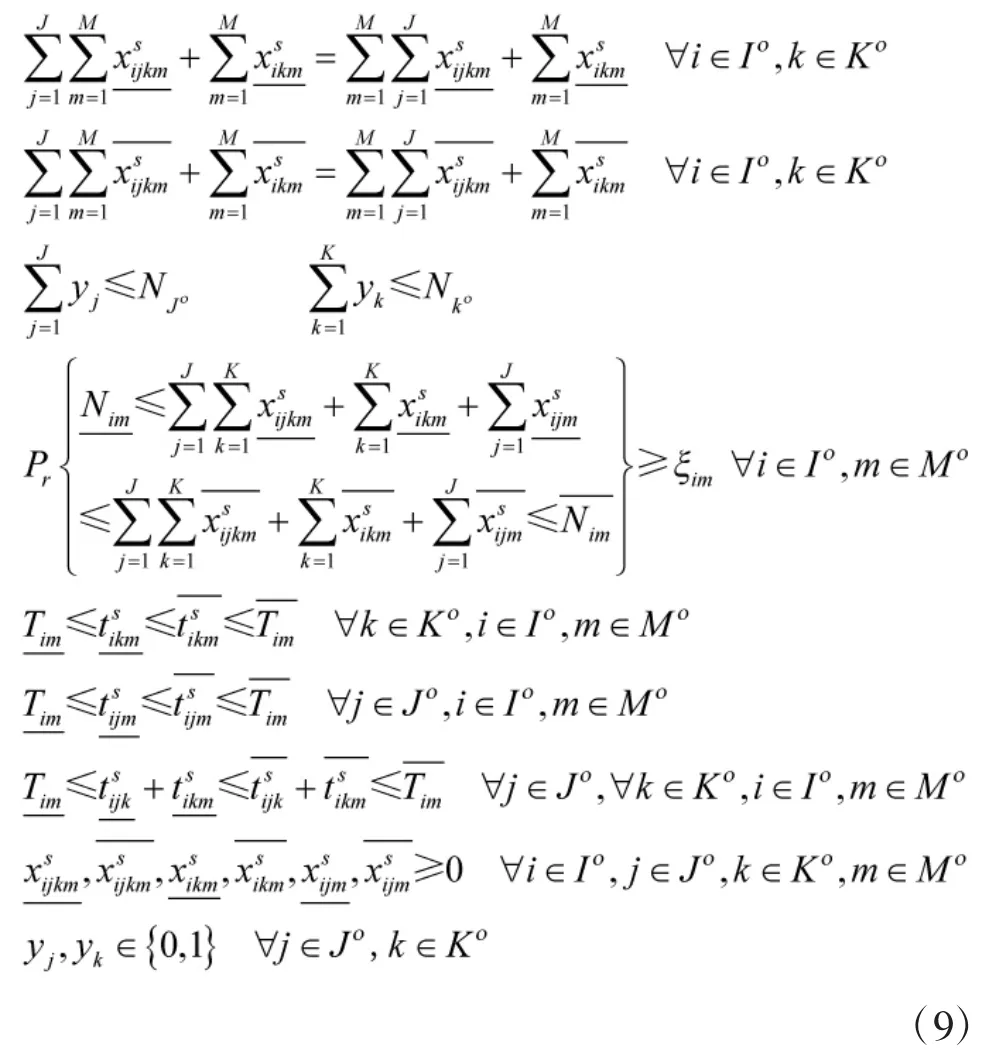
2 模型求解的两阶段算法设计

经过转化，问题转变成包含0-1整数变量的混合整数规划模型。由于模型中既存在随机优化搜索的求解，同时还包含非线性子优化问题，故可采用两阶段优化算法［13］进行求解。在问题求解的第1阶段，解决多种类物资容量有限的设施选址问题，即确定yj、yk的数值，根据Marvin等［14］对不同算法的比较分析，可知禁忌搜索算法［15］在解的质量、求解速度方面表现较好，因此，在问题求解的第一阶段采用禁忌搜索算法进行选址求解，将问题转化为运输问题，第2阶段采用MATLAB进行求解。禁忌搜索过程如下:

①以选址方案Y={yj，yk}构造问题的解时表示选择在j处备选点建立区域配送中心，在k处备选点建立基层资源点。

②将当前解中的0、1元素进行交换，以此邻域映射规则获得当前解的邻域解集。

禁忌表的长度Lmax设为定值，在第k次迭代过程中，选择某个移动后，将禁忌表中所有移动的非0禁忌值均减少1，并将当前进行的移动操作所对应的禁忌表中的元素设定为Lmax。

④采用③中的禁忌规则对所有邻域解集中的解进行筛选，从而得到当前解的候选解集。

⑤当迭代次数超过Tmax，或目标函数值持续无改进的次数超过Tr_max时，迭代终止。

综上，基于禁忌搜索的模型求解过程如下:

Step1初始化禁忌表，生成初始解Ynow，计算该选址方案下的优化结果；

Step2检测终止规则，若满足终止规则，转Step3。否则，依据②中的邻域映射规则生成当前解的邻域解集合，并依据③中的禁忌规则产生当前解Ynow的候选解集；若候选解集非空，则对候选解进行计算，选择评价值最佳的解Ynext，以Ynext更新Ynow，若候选解集合为空，则从当前解的邻域解中选择最佳的解Ynext加以解禁，更新下一迭代过程的起始解Ynow；更新禁忌表，重复Step2；

Step3停止计算，输出结果。

通过上述方法求解得到较优的选址方案Y={yj，yk}，相应的区域配送中心、基层资源点集合分别为J0o、K0o，则问题可转化为一个在运力约束和时间约束条件下的运输问题，分析该模型可知，经确定性转化，模型转变成一个混合0-1整数规划问题，采用MATLAB进行计算求解。

转化后的数学模型为:

3 实例设计与结果分析

现需在一定的区域内构建装备器材供应网的区域子网，在该区域内有3个备选的区域配送中心，7个备选的基层资源点，4个部队需求点对于3种器材的需求待满足。区域配送中心的数量限定为1个，NJo=1，基层资源点的数量为4个，NKo=4。各备选区域配送中心、备选基层资源点的供应能力（单位:件）、固定建设成本（单位:元）以及需求点的需求量（单位:件）、保障时间（单位:min）数据分别见表1、表2，各节点之间的供应保障时间见表3。

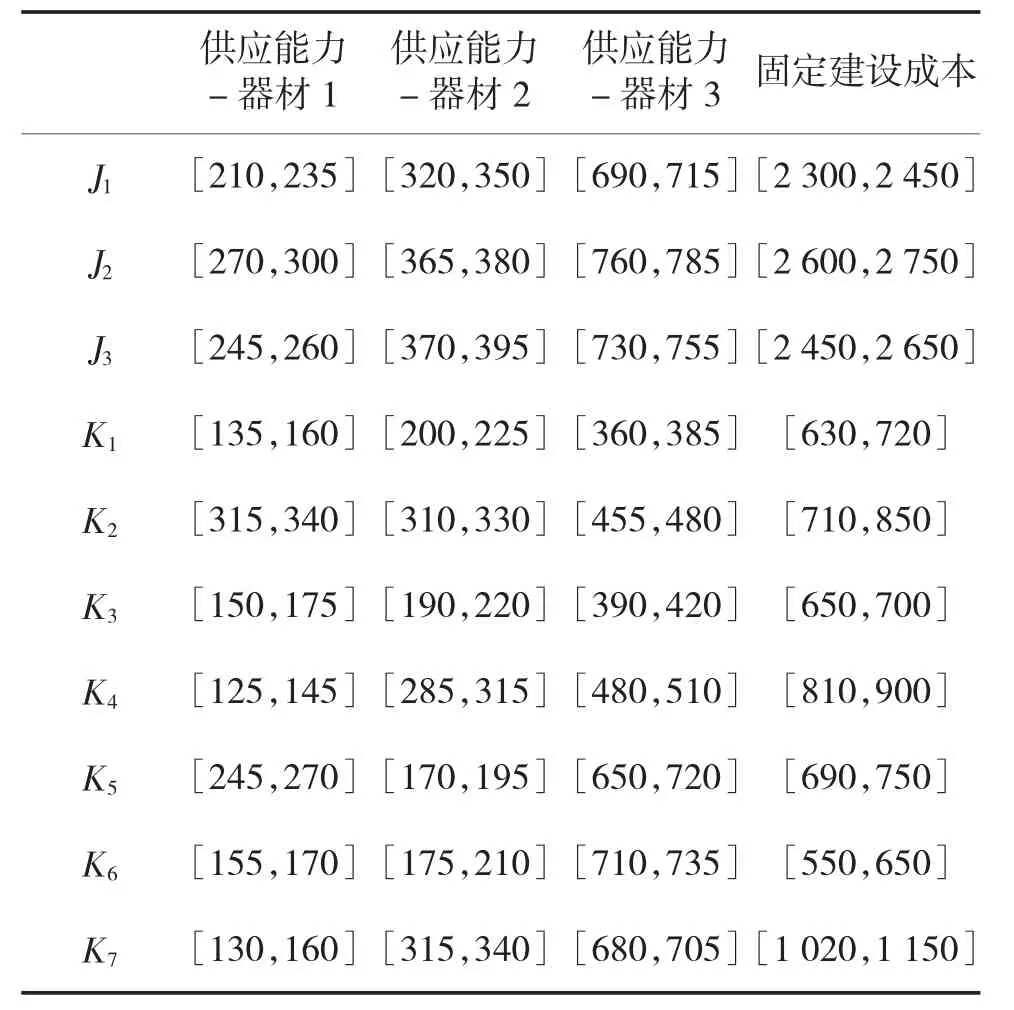
表1 配送中心、基层资源点的供应能力、固定建设成本数据

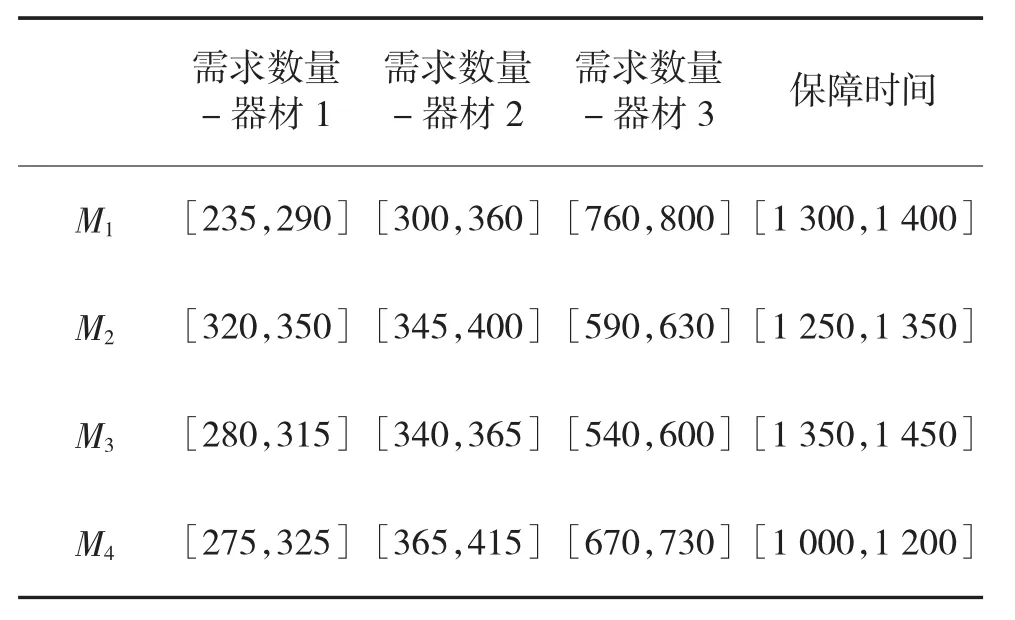
表2 部队需求点的需求数量、保障时间数据

定义初始种群Ue，算法参数设置如下:Tmax=300，Tr_max=3，Lmax=5，σ=120，在不同的风险因子ψ=0.2，0.6，0.9和最大偏差dmax=300，500下利用MATLAB进行仿真计算，结果如下页表4所示。

分析表4可知:在不同的风险因子和最大偏差情况下，区间不确定优化问题求解得到的最优解也存在一定的差异。在同样的风险因子ψ下，不同dmax对应的求解结果不同，而在同样的dmax下，不同ψ对应的求解结果也不同。这表明本文设计的模型和算法不仅能够获取区间最优解，还具有在不同类型场景下决策的优势，区间最优解反应出需求的不确定性造成的目标变动情况，而决策方案的不同则取决于决策者的决策态度和决策取向。对比表4中各约束条件下的最优解和对应的决策方案，可知在ψ=0.2和dmax=550的场景下，决策具有较大的优势，但其最优解的区间上界与区间下界的值相差较大，这也直接反映出装备器材供应网的不确定性。在ψ=0.2下，不同dmax对应问题的仿真决策结果如表5所示。

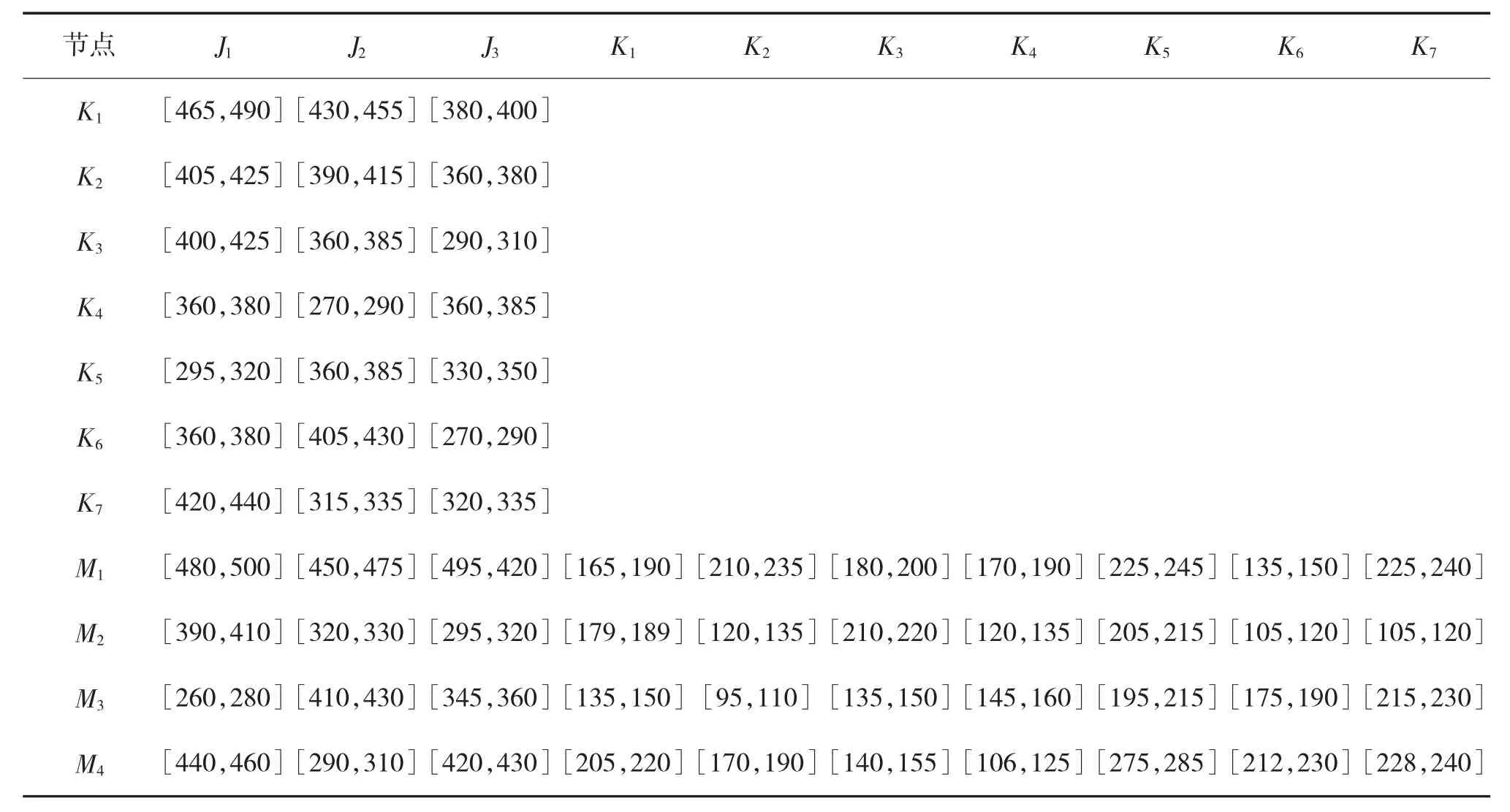
表3 区域配送中心向基层资源点、基层资源点向部队需求点供应器材的保障时间

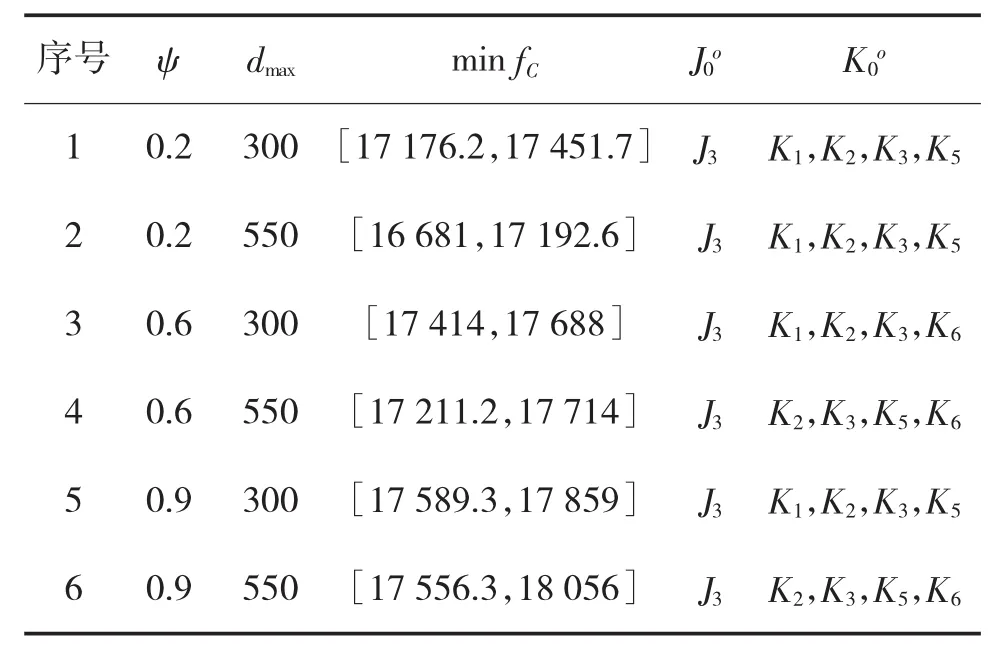
表4 不同ψ、dmax参数下的仿真计算结果

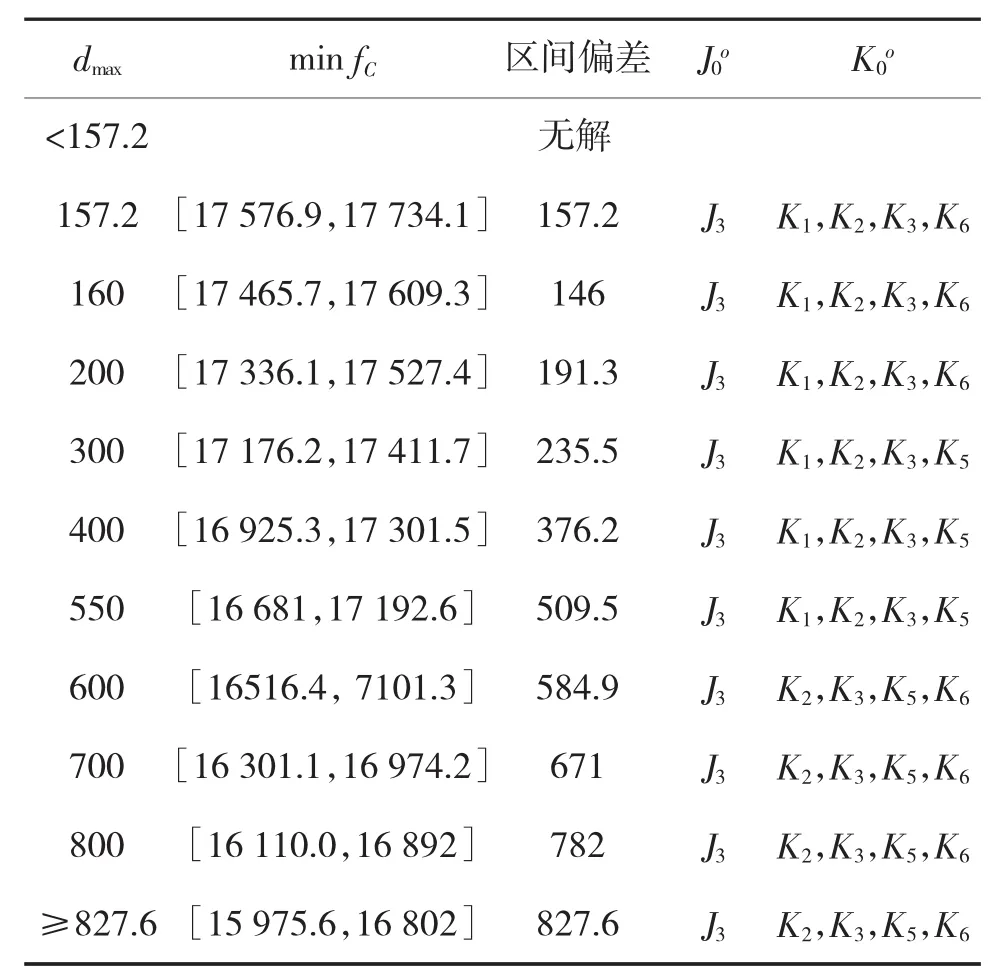
表5 不同dmax参数下的仿真决策计算结果（ψ=0.2）

分析表5可知:在给定的dmax约束下，仿真运算结果的区间偏差均小于dmax，如表中191.3＜200，509.5＜550等，即在满足特定的参数ψ和dmax约束下，均能求得相应的区间最优解。但是区间解的区间大小必须满足一定的限制条件，否则无法得到最优解，该实例中，在dmax＜157.2的场景下，模型无解，在预先设定参数时，运算偏差不能小于157.2；而在dmax≥827.6的场景下，区间最优解minfC的值保持在［15 975.6，16 802］的范围不变，求解结果完全一致，即在设置最大偏差参数dmax时，不能随意设置，不能随意减少或者扩大。

表6 不同算法的计算结果比较（ψ=0.2，dmax=550）

表6比较了不同算法的计算结果。在需求不确定条件下，除区间规划外，也可采用随机规划或者模糊规划进行确定性转化求解，但是这3种求解策略存在一定的差异性，尤其是在区间解的比较和以决策者的不同偏好为场景的决策上差异较大，本文模型与算法能求解得到更低的总成本。此外，本文算法所需运算时间也比其他算法的运算时间要短，表明本文算法具有更高的效率和更好的效果。

4 结论

装备器材供应网的规划过程中涉及要素多，存在多种不确定性，对我军装备器材供应保障决策带来了难题。为此，有针对性地对不确定条件下的装备器材供应网的规划问题进行研究，更是意义重大。结合区间规划理论的发展，采用区间分析方法，用区间数度量供应网规划中不确定性变量，并根据区间运算规则将模型简化，根据模型特点，结合实例，设计采用基于禁忌搜索的两阶段求解算法，为装备器材保障决策人员提供良好的辅助决策，有助于保障效率的提高。

区间规划方法的应用，能够较好地适应参数的变化属性，反映出决策者在追求问题最优解时的不同偏好及承担的风险程度。实例分析验证了基于禁忌搜索的两阶段求解算法的有效性，但仍需要探讨搜索速度更快、性能更加优化的求解算法，这也是下一步努力的方向。

［1］任骥，郑晓蕾.战场不确定环境下考虑敌方打击的后勤供应网络设计［J］.火力与指挥控制，2014，39（6）:126-130.

［2］傅学庆，马良，郭传福，等.基于最大效能通路的核心装备保障网络构建方法［J］.四川兵工学报，2014，35（7）: 29-32.

［3］张勇，杨宏伟，杨学强，等.基于复杂网络理论的装备保障网络模型研究［J］.上海理工大学学报，2012，34（5）: 429-434.

［4］王文峰，刘亚杰，郭波.战役装备维修保障网络设计问题研究［J］.兵工学报，2008，29（12）:1501-1508.

［5］张国防，何莉辉.基于不确定优化解的供应链优化模型研究［J］.产业与科技论坛，2011，10（22）:228-229.

［6］刘电霆，李明.产品绿色设计多重广义算子模型及不确定优化［J］.机械设计与制造，2014（5）:267-272.

［7］MOORE R.Method and application of interval analysis［M］. London:Prentice-Hall，1979.

［8］孙玉华，曾庆铎，王来生.区间规划问题的Wolfe型对偶理论［J］.江西师范大学学报（自然科学版），2012，36（6）: 594-597.

［9］孙玉华，许平，王来生.区间规划问题的最优性条件［J］.运筹与管理，2014，23（1）:39-43.

［10］苏白云.一种运用Vague集理论转化区间运输规划的方法［J］.数学的实践与认识，2013，43（4）:193-199.

［11］张相斌，倪友谊.网格环境下制造资源优化配置的区间规划模型［J］.数学的实践与认识，2012，42（6）:17-24.

［12］李利华，胡列格，符卓.复杂物流网络区间规划模型及算法［J］.系统工程，2012，30（4）:117-122.

［13］张春江，李宪民.基于运输费用折扣的供应链网络设计模型［J］.物流技术，2015，34（5）:214-216.

［14］MARVIN A，SUKRAN N，BASHEER M.An empirical comparison of tabu search，simulated annealing，and genetic algorithms for facilities location problems［J］.International Jour nal of Production Economics，2006，103（2）: 742-754.

［15］梁旭，黄明，宁涛，等.现代智能优化混合算法及其应用［M］.北京:电子工业出版社，2014.

Design Model of Equipment Materiel Supply Network under Uncertain Condition

YU Shuang-shuang1，WANG Tie-ning1，LI Ning2，XU Sheng-liang3
（1.Academy of Armored Force Engineering，Beijing 100072，China；2.Unit 78416 of PLA，Chongqing 400054，China；3.Military Representative Office in No.618 Factory，Beijing 100072，China）

Equipment materiel supply network is the importance cornerstone of equipment materiel supply support，its designing problem is one of the important strategy decisions of our military equipment material support process.In view of the node uncertainty，side uncertainty and demand uncertainty，the model of equipment materiel supply network consisting of several regional supply subnetworks under uncertain condition is explored.Aimed at the characteristic of the problem，interval analysis theory is adopted to measure and operate the uncertain factors and variables in designing materiel supply network，and the uncertain designing model is carried out as a result.Interval operation is applied to convert the uncertain model into determinate mixed integer programming model，and then the two-stage approach based on Tabu Search algorithm is designed to solve the model.The solution result of the model under the circumstance with different parameters is achieved respectively，and the result using the method in the paper is compared with fuzzy programming and stochastic programming. The result shows that the operability of the model and solution is stronger.

uncertain condition，supply network，design model，tabu search algorithm，interval programming

E92；TP301

A

1002-0640（2017）04-0079-06

2016-02-26

2016-04-18

军队科研计划基金资助项目

于双双（1987-），女，湖北枣阳人，博士研究生。研究方向：装备信息管理与决策。