基于量子双向RRT算法的多平台反舰导弹协同航路规划*

张承果，丁勇，申兴盼

（南京航空航天大学自动化学院，南京211106）

基于量子双向RRT算法的多平台反舰导弹协同航路规划*

张承果，丁勇，申兴盼

（南京航空航天大学自动化学院，南京211106）

针对反舰导弹航路规划面临的动态威胁环境和多平台协同打击问题，提出了一种基于量子双向RRT算法的反舰导弹协同航路规划方法。采用动态坐标设置动态威胁，实时地避开动态威胁；通过取预规划终点方法，实现对目标的时间和空间协同打击；结合量子进化思想，将RRT算法中的扩展方向量子化表示，提出了一种量子双向RRT算法，并应用于航路规划。仿真结果表明，该方法可有效规避动态威胁和解决多平台反舰导弹航路规划的协同问题，并显著地改善了RRT算法的全局收敛性，得到了航程更短的航路。

反舰导弹，多平台，协同航路规划，动态威胁，量子双向RRT算法

0 引言

反舰导弹（Anti-ship Missile）是从舰船、岸基或者飞机上发射，用于攻击水面舰船的导弹［1-2］。通常反舰导弹的作战任务会面临复杂多变的战场环境和多平台协同作战，实现精确打击需要导弹良好的突防。因此，复杂环境下的协同航路规划成为了反舰导弹完成作战任务的关键。

目前，大多数反舰导弹航路规划研究主要针对静态威胁环境下建立规划空间［3-4］，动态威胁下的航路规划方法研究少有涉及。然而，实际战场环境是复杂多变的，只研究静态威胁下的战场环境不能满足实际需求；由于单平台反舰导弹打击突防效率欠缺，更多的时候需要多平台发射导弹进行协同攻击，目前针对多平台反舰导弹协同航路规划方法却鲜有讨论［5-6］；在算法研究上，应用于航路的规划方法众多，可分为基于几何学原理的航路规划方法［7-8］和基于智能型优化算法的航路规划方法［9-10］。其中，智能型优化算法采用自适应的搜索方法，更适用于解决航路规划的问题。在众多智能航路搜索算法中，RRT［11-13］算法（Rapidly-exploring Random Tree，RRT）是一种经典的路径规划方法，它的特点是逻辑流程较为简单，且易于实现。但是，搜索的随机性使算法极易陷入局部最优，导致所搜索解并非全局最优路径。

针对上述问题，本文首先以动态坐标设置动态威胁，实时地避开动态威胁；然后，通过取预规划终点方法实现航路的空间协同和时间协同；最后，结合量子进化思想［14］，对传统RRT算法进行改进，将随机扩展方向角进行量子化编码，提出一种QBRRT（Quantum Bidirectional Rapidly-exploring Random Tree，QBRRT）算法，并将其应用于反舰导弹的航路规划。

1 多平台反舰导弹协同航路规划问题

由于反舰导弹从起点到目标点的最优航路受到复杂的战场环境和反舰导弹自身性能的约束，搜寻多平台反舰导弹的协同最优突防航路问题，可转化为一定约束条件下搜寻最优解的数学问题。

1.1 障碍和静态威胁的规避

基于反舰导弹掠海飞行的特点，反舰导弹突防区域中存在着许多的障碍，敌方拦截平台和探测设备的威胁。本文所提出的航路规划方法中，障碍和威胁的规避规则如下。

假设反舰导弹处于中间航路点P（x，y）位置，设置静态威胁和障碍，对应威胁半径为RSTHi，障碍半径为ROBj。定义P点到障碍的距离dpo为:

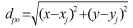
规避障碍规则为:

同理，定义P点到威胁的距离dps为

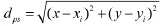
规避静态威胁规则为:

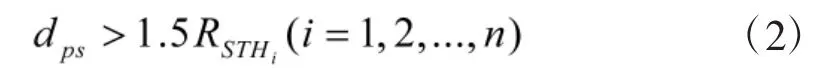
根据上述规则，要求中间航路点到障碍和威胁的距离满足式（1）和式（2），才能安全地避开障碍和威胁，否则重新选取扩展航路点。

1.2 动态威胁设置

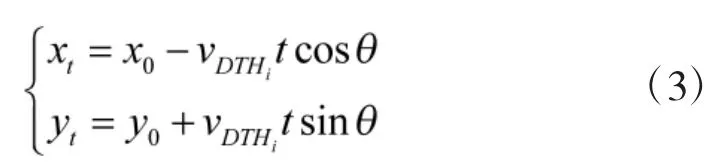
1.3 多平台反舰导弹协同打击

多平台反舰导弹协同打击目的是对目标进行全面地饱和打击，协同打击目标的关键在于解决多条航路的空间和时间协同。

1.3.1 空间协同打击

反舰导弹飞行过程是掠海飞行，航路交叉可能导致导弹弹头碰撞提前发生爆炸，从而导致攻击任务失败。因此，在协同航路规划过程中必须全程防止航路的交叉状况。而且，在末端制导阶段反舰导弹采用超低空飞行，反舰导弹需要从不同的攻击角度向目标射击，才能达到预想的快速隐蔽的饱和打击效果。

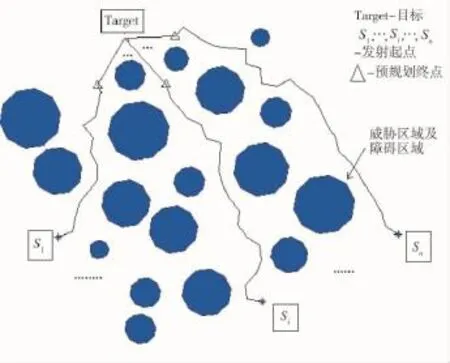
图1 预规划空间协同打击航路

如图1所示，空间协同航路规划是指在规划前，各平台以不同的攻击角度取临近目标点的预规划终点，对航路进行预规划，然后在末端打击阶段从不同的攻击角度对实际目标点进行打击，形成完整的协同打击航路，防止多条航路交叉，使得航路规划实现空间协同打击的目的。

1.3.2 时间协同打击

为了使反舰导弹能够可靠地突防敌方防控体系，实现饱和打击，不同平台反舰导弹要求几乎同时抵达目标点。由于多平台发射反舰导弹起点位置不同，存在飞行速度和航路航程的差异，根据这些差异调整各个平台发射的时间差便可实现时间协同。假设航路规划得到n个不同平台发射的反舰导弹规划航程分别为L1，L2，…，Ln，反舰导弹速度为v1，v2，…，vn，则所有反舰导弹中最大航程时间由式（4）可得:

根据式（4），得到最大航程时间。各平台的发射时间tj由式（5）给出:

各平台根据发射时间按顺序相继发射，即可达到多平台打击的时间协同。

2 航路规划算法

2.1 传统RRT算法

传统RRT算法扩展随机树的过程示意图，如图2所示。

图2 RRT算法扩展过程图示

其构造航路的思路是，首先将起始点定义为初始根节点xinit，以概率pg选择目标位置xgoal为随机点xrand，或者以概率1-pg随机选择一个规划空间里的点为xrand，从随机树的所有当前叶节点选出距离xrand最近的叶节点xnear，由该叶节点向xrand方向延伸步长为ls的距离，得到新节点xnew，判断xnew是否在障碍和威胁区域内，若不在区域内，将该新节点xnew记为树的新叶节点；若在障碍或威胁区域内，则舍弃该新节点，重新进行随机点xrand的选取。通过随机树连续的延伸扩展，当存在叶节点与目标节点距离足够近时，认为随机树构造完成，以距离目标点最近的叶节点开始向上搜索父节点，这样就形成了一条完整的由起始点到目标点的航路。

2.2 量子双向RRT算法

传统RRT算法在规划空间内采用随机采样点搜索航路，只要迭代次数足够，必定能够搜索得到符合突防要求的导弹航路。但是由于其随机搜索的特点，算法无效搜索代价比较高，使其搜索效率不高，搜索速度较慢。本文结合量子进化思想［15-16］，针对以上问题对RRT算法进行改进，提出了QBRRT算法。

2.2.1 航路编码与译码

首先取发射平台为随机树T1的根节点xinit1，取目标点为随机树T2的根节点xinit2。将扩展方向离散化为8个方向:0°、45°、90°、135°、180°、225°、270°、315°，这8个方向分别是45°的0、1、2、3、4、5、6、7倍。对这些倍数进行二进制编码，得到000、001、…、111 8个二进制数，它们表示的方向如图3所示。说明一个扩展方向角可以用3个量子态来表示，于是可以得到以下量子编码。

图3 量子化编码扩展转角

量子编码的一个量子比特的状态可以取0或 1，其状态可表示为，其中，α、β为两个复数，满足分别表示量子比特处于状态0和1的概率。则对扩展转角进行量子编码为

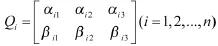
n为扩展次数。

量子译码过程为

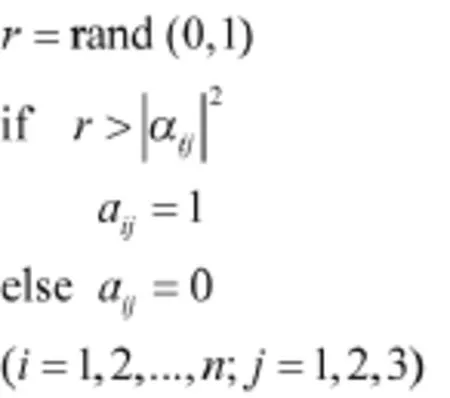
该节点量子译码为

根据量子编码译码取得扩展角为

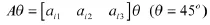
由xinit1向扩展角方向延伸步长ls，得到一个新节点xnew，根据式（1）和式（2），计算该新节点是否在威胁及障碍区域内，如果不在则取该新节点为随机树的一个叶节点。扩展下一节点时，取距离目标点最近的叶节点xnear向着扩展角方向延伸一个步长ls。同时，xinit2按上述扩展规律一起扩展。

根据前文所描述的反舰导弹航路规划空间，采用以上随机树扩展规律，分别以起始点和目标点作为随机树的根节点，将扩展方向角量子化，考虑威胁代价指标和障碍约束，扩展随机树直到两棵树交叉的时候，航路搜索结束，形成一条量子化编码的随机树航路。重复以上过程，形成多条航路，航路Pt的随机树量子编码为

量子译码为

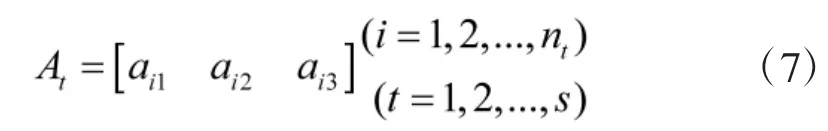
定义两棵树交叉表示T1存在一个叶节点与T2的某一叶节点距离小于一个步长ls，即

2.2.2 量子门更新

量子门更新使得个体向目前最好个体进化，即在Pt中选择出一条航程最短的航路Pbest，其航路随机树量子编码为Qbest，量子译码为

任意航路量子编码为

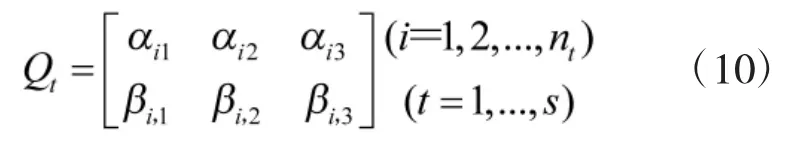
由于航路量子编码Qt量子位数量的不同，选择更新Qt的nmin位量子，这里

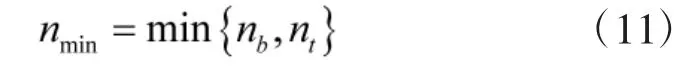
取Abest作为量子参考位，对Qt进行旋转门更新

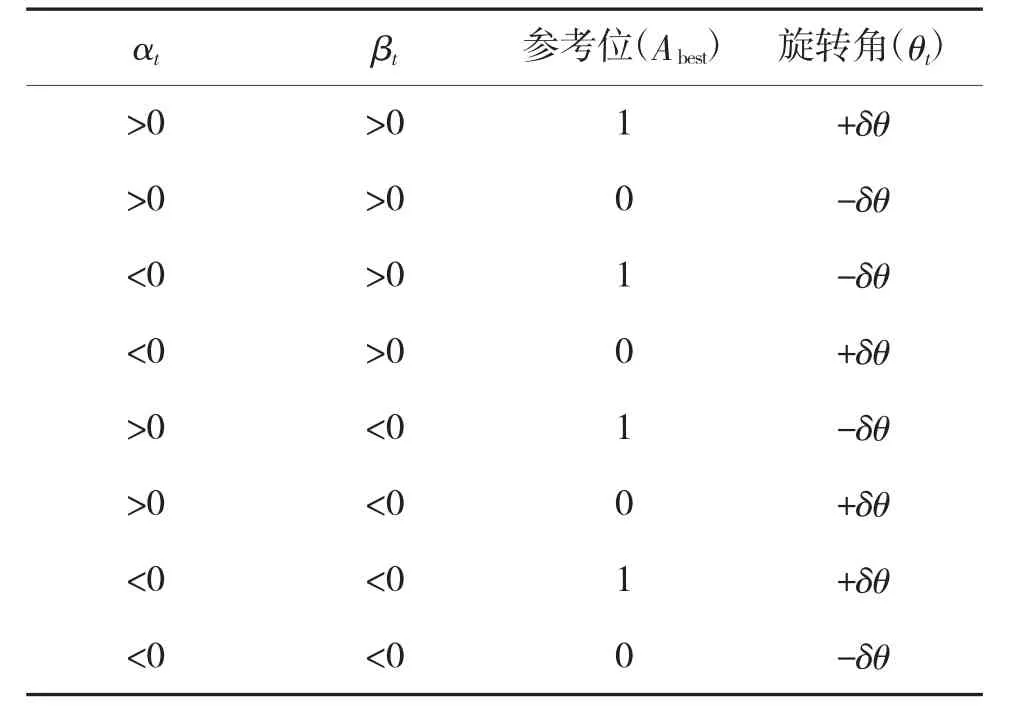
表1 旋转角

不同量子态对应量子门更新的旋转角选取规则如表1所示。参考位为目前所得航程最小个体量子译码Abest的对应基因位置的值，δθ这里取π/25。

根据量子更新思想，利用式（12）量子门更新航路，航路得到不断的进化。

综上，量子双向RRT航路规划算法步骤总结为:

Step2选取航程最短的个体为Pbest，其量子译码为Abest，航路坐标为，则Pathbest=Pbest；如果N= Nmax，算法迭代结束，最好个体为Pathbest。若N＜Nmax，则进入下一步。

Step3采用量子旋转门更新个体得到新的航路量子编码Qt'（t=1，…，s），量子译码为At'（t=1，…，s）。

Step4根据At'（t=1，…，s）扩展随机树可得到新的航路Pt'{（x1'，y1'），…，（xn'，yn'）}。跳转到Step2。

3 算法仿真及结果分析

仿真部分首先对QBRRT算法与RRT算法规划航路进行了比较；其次，对预规划终点方法解决多平台反舰导弹协同打击目标和动态威胁下的航路规划方法进行了仿真分析。

表2为威胁和障碍区域的中心坐标设置；表3为威胁和障碍区域半径设置。

表2 威胁和障碍中心坐标设置

表3 威胁和障碍区域半径设置

3.1 QBRRT算法与RRT算法规划航路比较

利用QBRRT算法和RRT对相同的单平台打击单目标作战任务航路规划仿真分析。如图4所示，作战区域大小为100 km×100 km，分别用QBRRT（迭代次数Nmax取50）和原始RRT算法搜索由平台Start（0 km，50 km）到目标Target（100 km，0 km）的航路。

图4 QBRRT与RRT算法航路规划比较

可以看出，由于原始RRT算法存在严重的随机性，搜索得到的航路航程明显过长。由于QBRRT算法在RRT算法基础上加入量子进化的思想，使得算法具有更优的全局收敛性，经过算法迭代，不断向最优解进化，算法搜索得到了航程更短的航路。

3.2 基于QBRRT算法的动态威胁下多平台反舰导弹协同航路规划

基于QBRRT算法的动态威胁下的多平台反舰导弹协同航路规划进行了仿真实验和分析。首先假设当前打击任务是由3个平台岸基S1（0 km，50 km）、舰船S2（50 km，0 km）和飞机S3（100 km，0 km）向目标舰船Target（100 km，0 km）发射反舰导弹进行协同打击。

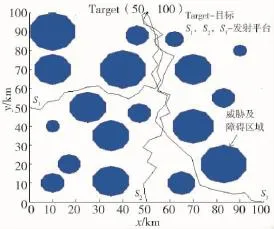
图5 未取预规划点的多平台航路规划

在图5中，威胁及障碍区域按照表2和表3参数进行设置。由图可以看出，由于未选取预规划终点，多平台的规划航路产生交叉，无法满足空间协同打击的目的。

在图6中，选取预规划航路终点T1（35 km，90 km），T2（55 km，80 km），T3（65 km，93 km）。在打击末段，由预规划终点以不同的攻击角度向目标实施打击，根据式（4）计算3个平台的发射时间。从而，实现多平台反舰导弹航路规划的空间和时间协同。

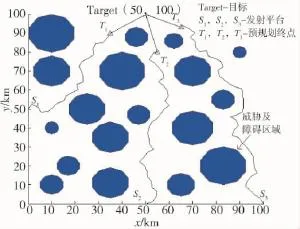
图6 取预规划点后的多平台协同航路规划

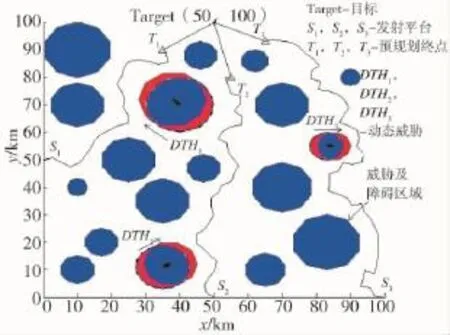
图7 动态威胁下的多平台协同航路规划

图7中，将表2和表3中的最后3个静态威胁设置为动态威胁，其余静态威胁及障碍区域保持不变。设置动态威胁中心起始坐标为DTH1（40 km，70 km）、DTH2（35 km，11 km）和DTH3（83 km，55 km），动态威胁半径分别为RDTH1=10 km、RDTH2=8 km、RDTH3=5 km，DTH1向西北方向运动，DTH2向东偏北30°方向运动，DTH1向东运动。动态威胁运动速度均定义为导弹巡航速度的1/20，以式（3）所计算得到的动态威胁坐标，根据动态威胁规避规则，航路未与动态威胁区域产生交叉或重叠，实现了在航路规划过程中合理地规避动态威胁。

4 结论

多平台反舰导弹协同航路规划是一个基于复杂环境的协同打击问题。为了得到更加优化的多平台协同打击航路，文中采用了动态坐标方法设置动态威胁，以保证航路规划过程中实时地躲避动态威胁；以选取预规划点的方法实现了多平台反舰导弹航路的空间和时间协同；对传统RRT算法进行改进，结合量子进化思想提出了QBRRT算法，有效地提高了传统RRT算法收敛性，减少了规划航路航程。

本文所提出的航路规划方法主要针对静态目标的作战环境来进行航路规划，未来的工作可扩展到对动态目标环境下的多平台协同航路规划方面进行深入研究。

［1］刘钢，老松杨，谭东风，等.反舰导弹航路规划问题的研究现状与进展［J］.自动化学报，2013，39（4）:347-359.

［2］高曼，刘以安，张强.优化蚁群算法在反舰导弹航路规划中的应用［J］.计算机应用，2012，32（9）:2530-2533.

［3］李红亮，宋贵宝，刘铁.基于自适应A*算法和改进遗传算法的反舰导弹航路规划［J］.弹箭与制导学报，2013，33（2）:7-11.

［4］刘钢，老松杨，侯绿林，等.约束引导的反舰导弹航路规划遗传算法［J］.弹道学报，2012，24（4）:11-17.

［5］曾家有，王国卫，钟建林，等.多平台舰舰导弹饱和攻击几个协同问题与模型［J］.兵工学报，2014，35（2）:256-261.

［6］李红亮，宋贵宝，李高春.反舰导弹协同攻击航路规划与重规划［J］.电光与控制，2012，19（12）:19-21.

［7］陈玉文.反舰导弹航路规划快速搜索算法［J］.系统仿真学报，2009，21（20）:6424-6435.

［8］刘钢，老松杨，谭东风.基于功能区域的反舰导弹逆向航路规划［J］.系统工程与电子技术，2011，33（4）:799-805.

［9］YUAN Z H，YAN J，LANG Z.Route planning for unmanned aerial vehicle（UAV）on the sea using hybrid differential evolution and quantum behaved particle swarm optimi-zation［J］.IEEE Transactions on Systems Man&Cybernetics Systems，2013，43（6）:1451-1465.

［10］MOHANTA J C，PARHI D R，PATEL S K.Path planning strategy for autonomous mobile robot navigation using Petri-GA optimisa-tion［J］.Computers&Electrical Engineering，2011，37（6）:1058-1070.

［11］ZANG X Z，YU W T，ZHANG L，et al.Path planning based on bi-RRT algorithm for redundant manipulator［C］//International Conference on Electrical，Automation and Mechanical Engineering，2015.

［12］XIE B.Fault tolerant motion planning of robotic manipulators based on a nested RRT algorithm［J］.Industrial Robot，2012，39（1）:40-46.

［13］KONG Y，PAN Y，CHEN X.A kind of two-stage RRT algorithm for robotic path planning［J］.International Journal of Wireless&Mobile Computing，2013，6（1）:34-38.

［14］CHUANPEI X U，DONG P.Network-on-Chip mapping research of quantum evolutionary algorithm［J］.Computer Engineering&Appli-cations，2011，47（1）:70-73.

［15］LIN C C，CHAKRABARTI A，JHA N K.Optimized quantum gate library for various physical machine descriptions［J］.Very Large Scale Integration Systems IEEE Transactions on，2013，21（11）:2055-2068.

［16］LAYEB A，SAIDOUNI D E.A new quantum evolutionary algorithm with sifting strategy for binary decision diagram ordering problem［J］.International Journal of Cognitive Informatics&Natural Intelligence，2010，4（4）:47-61.

Cooperative Path Planning for Anti-ship Missiles on Multi-platform Based on Quantum Bidirectional RRT Algorithm

ZHANG Cheng-guo，DING Yong，SHEN Xing-pan
（School of Automation Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 211106，China）

Aiming at the problems that anti-ship missiles on multi-platform cooperatively attack target in dynamic threatening environment，a cooperative path planning method for anti-ship missiles based on quantum bidirectional RRT algorithm is proposed.Setting dynamic coordinates are used to solve the problem that path avoid the dynamic threats in real time.The preplanned-destination method is used to achieve that anti-ship missiles attack the target collaboratively.By combining the traditional RRT algorithm with quantum evolution theory，the extended direction angle of RRT is represented by quantum states，a Quantum Bidirectional RRT algorithm（QBRRT）is proposed to search the path of anti-ship missiles.The simulation results show that this method effectively avoid the dynamic threat and solve the cooperative problem of path planning for anti-ship missiles on multi-platform.The QBRRT significantly improves the global convergence of the RRT algorithm and gets a shorter path for anti-ship missiles.

anti-ship missiles，multi-platform，cooperative path planning，dynamic threat，quantum bidirectional RRT algorithm

TJ765.2

A

1002-0640（2017）04-0036-06

2016-03-07

2016-04-24

国家自然科学基金资助项目（61374130）

张承果（1991-），男，贵州遵义人，硕士研究生。研究方向：智能决策。