一种长周期伪码信号的跳跃式扩展重叠捕获方法

刘芳，冯永新

（沈阳理工大学通信与网络工程中心，沈阳110159）

一种长周期伪码信号的跳跃式扩展重叠捕获方法

刘芳，冯永新

（沈阳理工大学通信与网络工程中心，沈阳110159）

随着直扩技术的发展，为提高应用系统的信号质量，出现了长周期伪码信号。然而，正是由于长周期伪码的出现及广泛应用，引发了系统接收的同步搜索误差大、速度慢等关键问题。为此，针对长周期伪码特性，考虑现有方法的局限和不足，提出了一种跳跃式扩展重叠捕获方法，通过扩展分段的跳跃式重叠技术来扩大搜索范围及提高处理速度。仿真结果表明，新方法在捕获性能及处理速度、检测概率等方面都明显优于现有的方法。此研究可以为扩频信号的高效同步及系统应用提供技术基础。

扩频通信，长周期伪码，捕获，仿真

0 引言

直接序列扩频（DSSS，Direct Sequence Spreading Spectrum）［1］，即:直扩，凭借其在保密、抗噪、抗干扰、高精测量等方面的优势，逐渐成为移动通信、卫星导航等领域的重要支撑。为更好地提高直扩应用系统的通信质量，提高抗欺骗能力，传统短周期扩频伪码已不能满足日益增长的抗干扰通信、高精测距等需求。为此，扩频伪码从较短周期，向长周期演进，如GPS（Global Position System）［2-3］系统中应用了周期为266.41天的P码、移动卫星通信系统中应用了周期大于一年的PIN码等。然而，正是由于长周期伪码的出现及广泛应用，也引发了系统接收的同步关键问题。考虑长周期伪码信号的近似无周期特性，当信号发射及接收终端时钟存在钟差时，在一次积累时间内本地伪码与接收信号可能无时间重叠，也即无相关性，从而出现时间不确定现象。随着钟差的进一步增大将引发搜索范围巨大的问题，为此相关处理速度也将骤然降低。从而必然引发接收端的同步搜索误差大、速度慢等关键问题。

近年来，相继呈现了一些以降低伪码搜索不确定度为主体的同步方法［4-8］，如XFAST法、均值法，以及在此基础上提出的压缩相关法、相位相干法、改进的FFT（Fast Fourier Transform）同步方法、时频域结合［9］、频域并行［10］等同步方法。其中，压缩相关法主要是对接收信号进行前端数据处理，进而通过建立特定的相关通道来提高适应性和同步速度；相位相干法主要是通过引入复杂的向量以及多层相位相干运算来减小噪声影响，并可以降低处理复杂度，但是上述方法在高采样率条件下考虑还不全面，不能满足高时效性需求。改进的FFT同步方法是对接收信号进行均值等数据处理、提高搜索范围，但是当高采样率处理时，不能满足时效需求；时频域结合方法是进行多通道并行Doppler补偿、均值及扩展处理，提高搜索速度，但在高动态情况下同步效率较低。

综合考虑搜索误差及处理速度的问题，较为有效的方法为分段相关捕获（SCA，Subsection Correlation Acquisition）及扩展重叠捕获（SSA，Spread Superposition Acquisition）方法。其中，分段相关类方法的主要思想是通过本地产生的扩频伪码进行分段处理，或是依赖接收信号中短码的周期进行分段，进一步对分段后的本地序列与接收序列进行循环相关运算，通过计算最大相关峰位置来估计伪码相位。扩展重叠类方法的主要思想是利用扩频伪码的良好自相关及互相关特性，对多段本地扩频伪码进行重叠处理来扩大搜索范围，重叠后的本地序列与接收序列进行循环相关运算，并通过峰值判决来估计伪码相位。分段相关类方法和扩展重叠类方法虽然都能够提高捕获速度，且可以有效估计伪码相位，但是在收发钟差偏差较大的条件下其搜索速度还有待提高。

1 跳跃式扩展重叠方法原理

考虑目前长周期伪码信号捕获技术的局限和捕获高效能需求，借鉴扩展重叠技术，利用积累时间和相关运算关系来选择分段，并控制分段的跳跃式重叠，从而提出一种跳跃式扩展重叠捕获（JSSA，Jumping Spread Superposition Acquisition）方法。

首先，对经过接收天线及降频、滤波等前端处理的接收序列进行积累，其积累长度为L，其积累的接收序列可表示为:

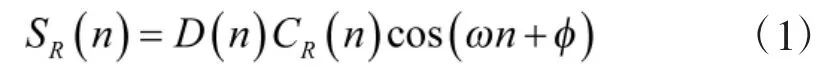
产生较长时间的本地扩频伪码序列CL（n），考虑扩频伪码的良好相关特性，对本地序列进行分段，分为N段，每段长度为L，但是各个分段间的序列并非连续的，而是跳跃性的，即各个段间舍弃L/2长度的序列，其原理如图1所示。分段后的本地序列分别记为

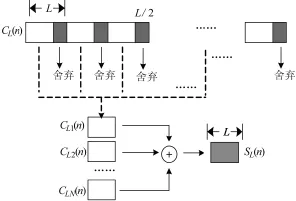
图1 跳跃式扩展重叠原理

对分段后的各段序列进行重叠处理，过程如式（2）所示。

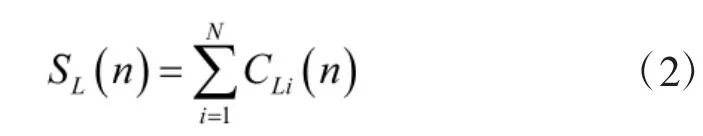
然后，接收序列与重叠后的本地序列进行循环相关运算:

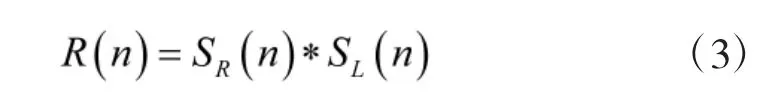
相关运算后，对长度为L的相关结果进行峰值计算如式（4），并利用其与判决门限比较，如果小于门限则重新产生本地序列以及进行上述处理，如果大于门限则表明当前的本地序列与接收信号有相位的重回位置，因此，继续执行。

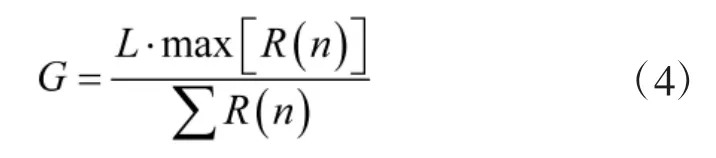
进一步，接收序列分别与本地序列CL1（n）、CL2（n）、…、CLN（n）进行循环相关运算如式（5），分别记为，其中，i的取值范围为1~N，从而得到R1（n）、

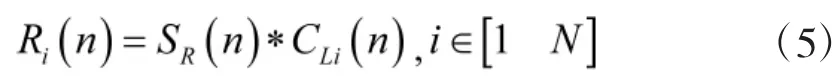
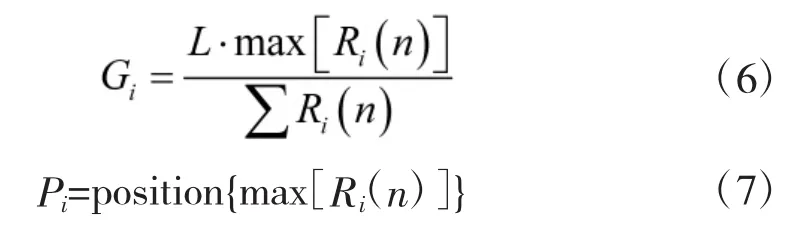
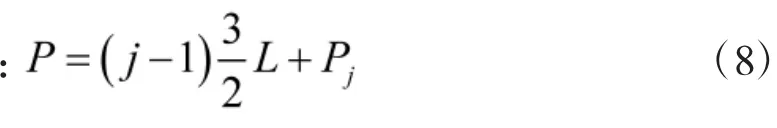
2 仿真分析

为了验证JSSA法的有效性及优越性，从对比角度出发，与较为有效的SCA法和SSA法进行比较分析，其仿真参数为:伪码速率1.023 MHz，中频频率为2.046 MHz，接收信号积累10 ms，一次搜索范围为750 ms。

首先，考虑相关峰值结果作为捕获成功的重要指标，其相关峰值越大则捕获成功概率越大，而相关峰值越低则捕获结果越模糊；此外考虑绝对峰值的高低受环境及干扰影响较大的因素，为此，设置最大峰值与平均峰值的比值作为判决捕获方法的一项指标。随着SNR的变化，3种方法的峰值比（最大峰值与平均峰值的比值）变化趋势如图2所示。结果可见，随着SNR的逐渐增大，3种方法的峰值比都逐渐增大，相对而言，JSSA方法的峰值比最大，而SCA方法与SSA方法的峰值比较接近，且略低于JSSA方法。从而表明JSSA方法的捕获相关结果最优。进一步，从捕获方法的伪码估计误差角度出发，3种方法的捕获结果如图3所示。可见，随着信噪比（SNR）的增加，3种方法的伪码相位估计误差都在减小，而且3种方法在SNR＞-20 dB时都可以达到估计误差近似为0，即3种方法的工作条件适应性都为＞-20 dB。

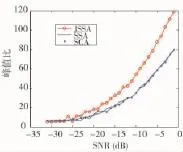
图2 捕获峰值比结果

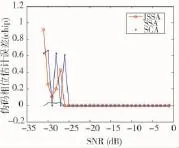
图3 捕获伪码相位误差结果

进一步，考虑长周期伪码信号捕获的搜索范围巨大的问题，从处理速度角度出发进行对比分析。一次性搜索750 ms范围条件下，3种方法的处理时间如图4所示，可见，SCA方法的处理速度最慢，SSA方法的处理速度居中，而JSSA方法的处理速度相对最快。进一步，当搜索范围扩大至75 s时，3种方法的处理速度变化如图5所示，可见，随着搜索范围的增大，3种方法的处理时间也都增加，但是相对而言，JSSA方法的处理速度明显优于SCA方法和SSA方法，为此，依据图4和图5的结果及分析，验证了JSSA方法的捕获速度明显优于其他两种方法，而且在搜索范围越大的条件下其搜索速度改善的越明显。

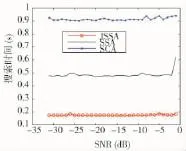
图4 一次搜索条件下捕获时间结果

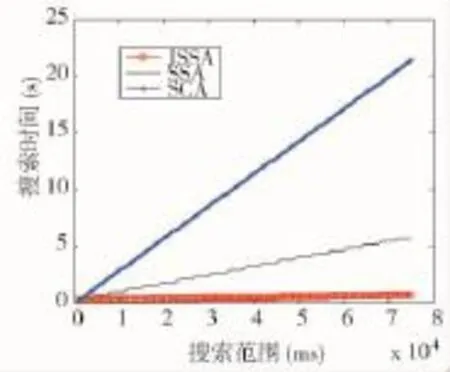
图5 大搜索范围条件下捕获时间结果

最后，考虑捕获概率作为衡量接收机捕获目标信号能力的重要依据，为此，从不同SNR角度出发，进行信号检测概率的对比分析。设定恒定虚警概率pfa=0.01条件下，测试结果如图6所示。结果表明，在同等条件下JSSA方法的主相关峰的检测概率优于其他两种方法。

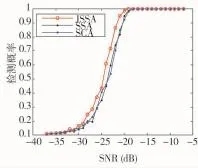
图6 检测概率结果

3 结论

考虑长周期伪码信号的近似无周期特性，当信号发射及接收终端时钟存在钟差时，将出现时间不确定现象，随着钟差的进一步增大将引发搜索范围巨大的问题以及处理速度骤然降低的问题。综合考虑搜索误差及处理速度的问题，提出了一种JSSA方法。通过仿真分析表明，JSSA方法的峰值比最大，即捕获性能优于现有的SSA和SCA方法；其有效工作SNR为不低于-20 dB。而且，在搜索范围较小及较大的条件下，JSSA方法的处理速度都明显优于SSA和SCA方法；此外，JSSA方法的检测概率也优于其他两种方法。

［1］CHUNG S，MCLANE P.Code hopping-direct sequence spread spectrum to compensate for intersymbol interference in an ultrl-wideband system［J］.IEEE Transactions onCommunications，2008，56（11）:1785-1789.

［2］SUBBURAJ K，BHATARA S，TANGUDU J，et al.Spur mitigation in high-sensitivity GNSS receivers［J］.IEEE Transactions on Circuits and Systems II:Express Briefs，2014，61（2）:100-104.

［3］KONG S H.A deterministic compressed GNSS acquisition technique［J］.IEEE Transactions on Vehicular Technology. 2013，62（2）:511-521.

［4］CHEN T W，WANG J，FAN X，et al.A research of carrier tracking loop for high hopping rate DS-FH Receiver［C］// IEEE International Conference，Signal Processing，Communication and Computing（ICSPCC），2013:1-5.

［5］BINHEE K，KONG S H.Design of FFT-based TDCC for GNSS acquisition［J］.IEEE Transactions on Wireless Communications，2014，13（5）:2798-2808.

［6］HSIRH W H，CHANG C F，KAO M S.Efficient acquisition algorithm for long pseudorandom sequence［J］.IEEE Transactions on Aerospace and Electronic Systems，2014，50（3）: 1786-1797.

［7］TA T H，QAISAR S U，DEMPSTER A G，et al.Partial differential postcorrelation processing for GPS L2C signal acquisition［J］.IEEE Transactions on Aerospace and Electronic Systems，2012，48（2）:1287-1305.

［8］章兰英，袁嗣杰，陈源.航天扩频测控系统中伪码捕获方法研究［J］.电子学报，2011，39（6）:1471-1476.

［9］刘芳，冯永新.一种解决时频不确定问题的长码捕获算法［J］.航空学报，2013，34（8）:1924-1933.

［10］田明浩，冯永新，潘成胜.一种基于P码的频域直接捕获算法的研究［J］.电子学报，2007，35（3）:549-552.

［11］刘正堂，薛寒，王军，等.分布式干扰对扩频接力通信干扰效果分析［J］.2013，38（12）:92-95.

A Jumping Spread Superposition Acquisition Method for Long Period Pseudo Code Signals

LIU Fang，FENG Yong-xin
（Communication and Network Institution of Shenyang Ligong University，Shenyang 110159，China）

With the development of Direct Sequence Spread Spectrum technology，the long period pseudo code signals emerged in order to improve the signal quality of the application system.Whereas，the synchronization problems of the search error and the processing speed are derived by the long period pseudo code.Thus，a jumping spread superposition acquisition method is proposed，through studying the signal mechanism and characteristics based on the long period pseudo code，as well as the deficiencies and limitations of existing acquisition methods.The simulation results demonstrate that the new method is better than the traditional algorithms in the acquisition performance，the processing speed and the detection probability.The research will provide the technical foundation to the efficient spread spectrum signal synchronization and system application.

spread spectrum communication，long period code，acquisition，simulation

TP391.9

A

1002-0640（2017）04-0033-03

2016-02-18

2016-04-27

国家自然科学基金（61501309）；中国博士后科学基金资助项目（2015M580231）

刘芳（1979-），女，黑龙江伊春人，博士，副教授，研究生导师。研究方向：扩频通信、卫星导航。