基于稀疏子空间聚类的人脸识别方法*
张彩霞,胡红萍,白艳萍
(中北大学理学院,太原030051)
基于稀疏子空间聚类的人脸识别方法*
张彩霞,胡红萍,白艳萍
(中北大学理学院,太原030051)
在现有的稀疏子空间聚类算法理论基础上给出两种稀疏子空间聚类优化算法:稀疏线性子空间聚类和稀疏仿射子空间聚类。这两种优化算法针对不同的数据集会有不同的聚类效果。通过稀疏表达得到不同的稀疏系数矩阵,把稀疏系数矩阵应用到较为简单的改进的正则化谱聚类算法中实现聚类。应用Yale B数据对人脸图像进行识别分类得出:采用稀疏线性子空间聚类算法优于稀疏仿射子空间聚类算法;在算法执行时间上和算法聚类错误率比传统的稀疏子空间聚类较为快速高效。
子空间聚类,稀疏子空间聚类,谱聚类算法,人脸识别
0 引言
在很多实际应用中,高维数据无处不在,如计算机视觉、图像处理、运动分割、人脸识别等。实际上,高维数据可以被相应的低维子空间分别表示。
近年来,子空间聚类在压缩感知问题上的应用已吸引了很多学者的注意,在信息科学上是一个很热的研究领域。子空间聚类的目的在于把高维数据划分在其潜在的子空间并应用到尽可能多的领域中。子空间聚类算法有4种:迭代法[1-2],代数法[3],统计法[4]和基于谱聚类方法[5-7],而前三种方法都需要知道子空间的个数和维数或对数据初始值,噪声,奇点比较敏感,谱聚类算法利用数据点之间的信息建立相似性,能够很好地避免上述缺点。
稀疏子空间聚类是基于谱聚类提出一种稀疏表达的聚类方法。Elhamifar等[8]利用稀疏恢复算法的先进性提出一种稀疏子空间聚类算法(Sparse Sub space Clustering,SSC),通过稀疏表示(Sparse representation,SR)构造相似度矩阵,并应用到谱聚类算法中,从而聚类数据,高维数据空间可由线性或仿射子空间稀疏表示,得到两个稀疏最优化算法:稀疏线性子空间优化算法,稀疏仿射子空间优化算法。本文首先在此理论基础上应用Yale B数据对各种不同的人脸图像识别、分类。
1 稀疏子空间聚类
稀疏子空间聚类是一种全新的数据聚类方法,是目前机器学习、计算机视觉、图像处理、模式识别等领域的研究热点。
稀疏子空间聚类[8]的基本思想是:设有N个D维数据,处于RD空间的n个线性或仿射子空间中,子空间的维数分别为,将数据表示为所有其他数据的线性组合,


其中,系数矩阵Z∈RN×N满足:当xi和xj属于不同的子空间时,有Zij=0,属于同一子空间时Zij≠0,式(2)用数据集本身表示数据,称为数据的自表示。若已知数据的子空间结构,并将数据按类别逐列排放,则在一定条件下可使系数矩阵Z具有块对角结构,即
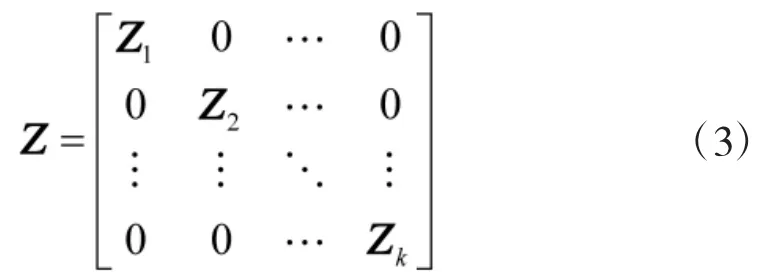
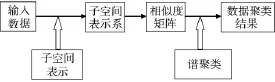
图1 稀疏子空间聚类的流程
通常,稀疏子空间聚类基于系数向量的一维稀疏性或系数矩阵的二维稀疏性来建立高维数据在低维子空间的表示,利用表示系数矩阵Z构造数据的相似度矩阵,最后利用谱聚类算法得到最终的聚类结果。图1描述了稀疏子空间聚类的流程。
2 稀疏最优化算法
位于线性或仿射集合的高维数据可以稀疏地被同一个子空间的点线性或者仿射表示。本文通过文献[8]中稀疏表示技巧获得高维数据的稀疏表示。
2.1 高维数据空间由线性子空间稀疏表示
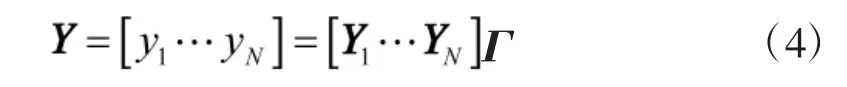
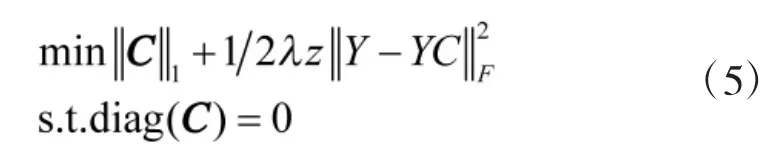
2.2 高维数据空间由仿射子空间稀疏表示
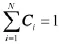
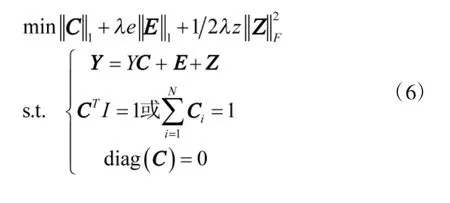
其中,C为稀疏系数矩阵,E为稀疏奇异值矩阵,Z为噪声矩阵,系数
本文的算法不需要提前知道子空间个数和维数最优化的求解通过ADMM(Alternating Direction Method of Multipliers)算法下完成[9]。
3 正则化谱聚类算法
谱聚类算法[10]是建立在图谱理论基础上的一种重要的数据聚类的方法,首先根据给定的数据集建立数据间的相似度矩阵,然后构造加权图,通过寻找图的最优划分实现数据聚类的目的,相似度矩阵建立的方法有很多种,本文采用上节所述稀疏表示的方法,获得相似度矩阵,然后,根据加权图的最优划分准则,产生不同的Laplacian矩阵:
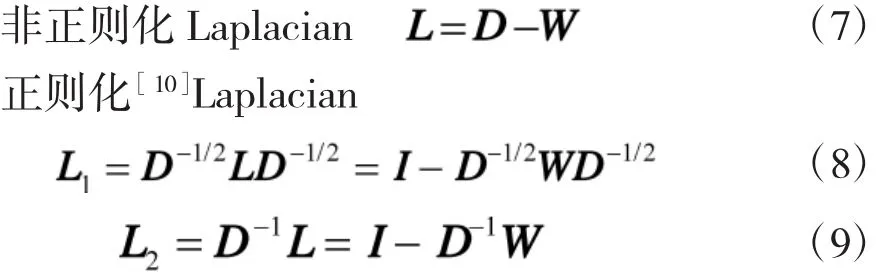
谱聚类算法[11]寻求相似加权图的最优划分,要求类间切割权值最小而类内相似权值最大,然而非正则化谱聚类有时不能满足类内相似权值最大这个要求,而正则化谱聚类能够很好地满足这两个条件。因此,正则化的算法优于非正则化谱聚类算法。谱聚类算法涉及到特征向量的计算,两种正则化Laplacian矩阵的特征可知,L2特征向量计算L1比特征向量更为简单,算法执行时间较为快速。由L2包含聚类信息的特征向量组构成的矩阵具有分段常值性,所反映的聚类信息比较明显。而由L1包含聚类信息的特征向量组构成的矩阵具有分段平行性,其所反映的聚类信息不如矩阵L2的明显[12]。在稀疏子空间聚类算法中,Elhamifar等选择了L1,而本文经过实验研究比较选择了L2。
4 最优化SSC算法
本文算法在获得稀疏系数矩阵之后,选择文献[10]的正则化谱聚类算法。
①把n维线性或仿射空间的数据点{yi}iN作为输入利用稀疏子空间式(5)或式(6),获得稀疏系数矩阵C,算法实现在ADMM算法下完成;
③根据稀疏系数矩阵建立相似加权图,每个数据点只与其稀疏表示中的数据点连接,不同子空间的数据点无连接,权值矩阵为;
④把相似加权图应用到谱聚类算法[10]中,求Laplacian矩阵L2,对其求特征值,子空间个数n为特征值零的次数,获得前n小个特征值,把其对应的特征向量形成N×n的矩阵U;
⑤把U的每一行作为n维空间的一个向量,对U进行K-means聚类,N行所对应的类就是其N个数据点对应的类。得出输出数据点所对应的类Y1,Y2,…,Yn。
5 实验结果与分析
本文的数据来自Yale B数据集,为1 024维的高维数据,包含38个不同人的人脸图像,每一个人在不同变换条件下的正面脸部图像有64个,每一个图像由1 024维向量表示,为了清楚地理解Yale B数据,把像素点表示为32×32的像素读成图片如图2所示。此高维数据空间可能由多个线性子空间组成或者由多个仿射子空间组成,利用前面提到的两类稀疏最优化算法,结合改进的谱聚类算法分别对不同人脸图像进行分类识别。

图2 两人的人脸图像
为突出本文数据选择优化算法和对优化算法作出的改进,实验选取了8个不同人的人脸图像,从算法聚类错误率和执行时间两方面作出比较。error1和error2表示稀疏线性和仿射子空间聚类结合正则化谱聚类L1聚类错误率。error3和error4表示稀疏线性和仿射子空间聚类结合正则化谱聚类L2聚类错误率。t1和t2表示稀疏线性子空间聚类结合L1和L2的算法执行时间。t3和t4表示稀疏仿射子空间聚类结合L1和L2的算法执行时间。N表示人脸图像个数,S表示分类个数。所有的算法均在MATLAB R2014a下运行。
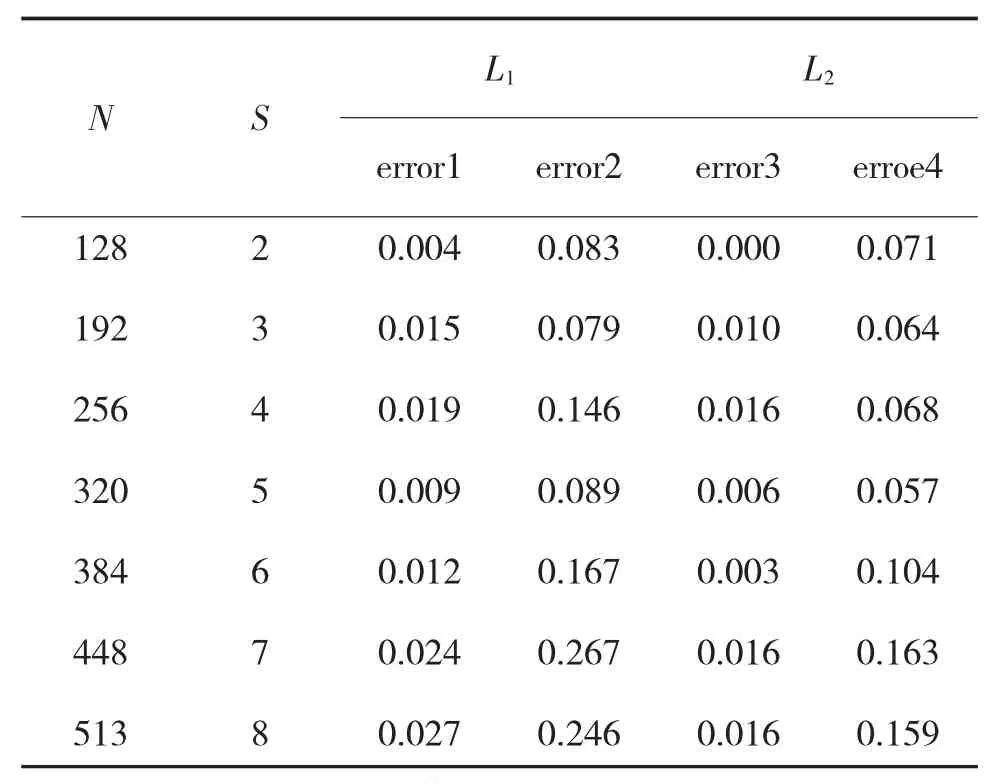
表1 算法聚类错误率
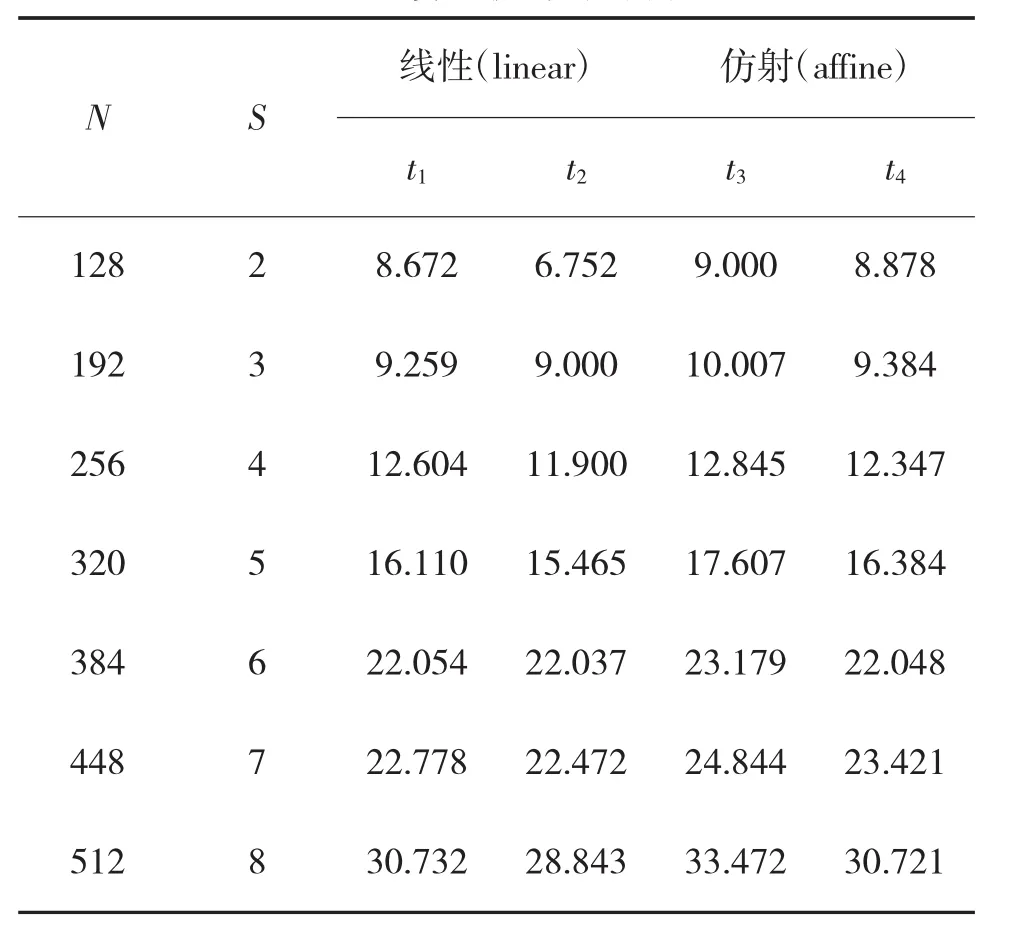
表2 算法执行时间(s)
从表1得出Yale B数据人脸识别应用稀疏子空间聚类结合正则化谱聚类L2聚类错误率低于L1:利用稀疏线性子空间优化算法聚类错误率低于稀疏仿射子空间优化算法聚类错误率。从算法执行时间上,L2较L1快速。
6 结论
本文指出Yale B数据集在稀疏线性子空间聚类效果优于稀疏仿射子空间聚类,而文献[8]的实验结果中稀疏仿射子空间聚类效果优于稀疏线性子空间。从而得出稀疏线性或仿射子空间聚类优化算法并不是对任何数据集聚类有效,两种优化算法聚类数据有选择性。应用改进的一种较为简单的正则化谱聚类算法L2比L1实时高效。
[1]TSENG P.Subspace clustering[J].Signal Processing Magazine,2001,28(2):52-68.
[2]HO J,YANG M H,LIM J,et al.Clustering appearances of objects under varying illumination conditions[C]//IEEE Conference on Computer Vision and Recognition,2003.
[3]COSTERIRA J,KANADE T.A multibody factorization method for independently moving objects[J].International Journal of Computer Vision,1998,29(3):159-179.
[4]TIPPING M,BISHOP C.Mixtures of probabilistic principal component analyzers[J].Neural Computation,1999,11(2): 443-482.
[5]WEISS Y.On spectral clustering:analysis and algorithm[J]. Neural Information Processing Systems,2001:849-856.
[6]YAN J,POLLEFEYS M.A general framework for motion segmentation:Independent.Articulated,rigid.non-rigid.Degenerate and non-degenerate[C]//in European Conf.on computer,2006:94-106.
[7]CHEN G,LERMAN G.Spectral curvature clustering(SSC)[J].International Journal of Computer Vision,2009,81(3): 317-330.
[8]ELHAMIFAR E,VIDAL R.Sparse subspace clustering:Algorithm,theory,and applications[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(11): 2765-2781.
[9]BOYD S,PARIKH N,CHU E,et al.Distributed optimization and statistical learning via the alternating direction method multipliers[J].Foundations and Trends in Machine Learning,2010,3(1):1-122.
[10]LUXBURG U.A tutorial on spectral clustering[J].Statistics and Computing,2007,17(4):395-416.
[11]欧阳佩佩,赵志刚,刘桂峰.一种改进的稀疏子空间聚类算法[J].青岛大学学报(自然科学版),2014,27(3): 44-48.
[12]苏木亚.谱聚类方法研究及其在金融时间序列数据挖掘中的应用[D].大连:大连理工大学,2011.
[13]封睿,李小霞.基于GLC KSVD的稀疏表示人脸识别算法[J].四川兵工学报,2014,35(4):88-92.
Face Recognition Method Based on Sparse Subspace Clustering
ZHANG Cai-xia,HU Hong-ping,BAI Yan-ping
(Faculty of Science,Department of Maths,North University of China,Taiyuan 030051,China)
We offer two kinds of sparse subspace clustering optimization algorithm,sparse linear space clustering and sparse affine subspace clustering,based on the existing theory of sparse subspace clustering algorithm.For different data gathering,these two kinds of optimization algorithm has different clustering results.In this paper,different sparse coefficient matrix by sparse expression is obtained.In order to achieve cluster,the sparse coefficient matrix is applied to relatively simple regularization of spectral clustering algorithm.Application of Yale B data,we recognize and classify face image:using sparse linear space clustering algorithm is better than the sparse affine subspace clustering algorithm;Comparing with the traditional sparse subspace clustering,it is more fast and efficient in the time of execution and error rate of algorithm.
subspace clustering,sparse subspace clustering,spectral clustering algorithms,face regulation
TP391
A
1002-0640(2017)04-0029-04
2016-02-16
2016-03-25
国家自然科学基金(61275120);2014年校自然科学基金资助项目
张彩霞(1989-),女,山西朔州人,在读硕士研究生。研究方向:现代最优化算法。

