不含辅助矢量的矢量形式六自由度弹道计算模型

王兆胜

(南京炮兵学院, 南京 211132)

0 引言

六自由度弹道模型在弹道仿真[1]、射表计算[2]、弹道落点预测[3]等领域有广泛的应用。文献[4]以瞬时弹轴方向的单位矢量x表示弹轴的空间姿态,给出了动量矩H的矢量形式。通过引入过程辅助矢量h=H/Iy,研究力与力矩与x和h关系,将弹丸质心运动方程和绕质心转动方程与x和h联系起来,在单一的地面坐标系下给出含有x和h的弹丸质心运动方程和弹丸绕质心转动方程,其特点是弹丸转动方程含有x和h两个矢量。能否在不引入辅助矢量h情况下,用单一的矢量x建立起弹丸绕质心转动方程,此时的矢量形式六自由度弹道模型分量形式如何,下面对此进行研究。

1 矢量形式的六自由度弹道方程组

地面坐标系采用文献[4]中的表示符号,即地面坐标系记为O-123,原点O在炮口断面中心,3个坐标轴记分别为1、2、3,其中1、3轴所在的平面过原点且平行于原点处地球的切平面,1轴指向射向,2轴在发射点垂直向上,3轴按右手法则确定。图1为地面坐标系示意图,地面坐标系O-123简记为坐标系[1,2,3]。

设弹丸质心运动速度为V(见图1),则弹丸质心运动方程为:

(1)

式中:ΣFi为弹丸飞行中各项气动力的合力;mg为重力;mΛ为科氏力。

设弹丸绕质心转动的动量矩为H,则绕质心转动的弹丸动量矩方程为:

(2)

式中:ΣMi为弹丸飞行中对质心的各项气动力矩之和。

设x为沿弹轴方向指向弹尖的单位矢量(见图1),对于轴对称弹丸,弹丸绕质心转动动量矩H为[4]:

(3)

式中:Ix为弹丸极转动惯量;p为弹丸绕弹轴的自转角速度;Iy为绕通过质心且垂直于x的任意轴的转动惯量。

将式(3)代入式(2),得弹丸动量矩方程为:

(4)

1.1 弹丸飞行中所受的气动力

弹丸飞行中所受的气动力包括空气阻力、升力、马格努斯力及俯仰阻尼力,设v为弹丸质心的相对速度,则:

(5)

式(5)右端中简略符号的含义如下:

(6)

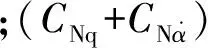
1.2 弹丸飞行中所受的气动力矩

弹丸飞行中所受的气动力矩包括极阻尼力矩、尾翼导转力矩(如果弹丸有尾翼)、俯仰力矩、马格努斯力矩及俯仰阻尼力矩。因此有:

(7)

式(7)右端中的简略符号含义如下:

(8)

1.3 矢量形式六自由度弹道方程组

将ΣFi的表达式(5)代入式(1),得：

(9)

将ΣMi的表达式(7)代入式(4),并考虑到x×(x×v)=(x·v)x-v,得弹丸动量矩方程为:

(10)

2 单一矢量形式的六自由度弹道模型

从方程(10)中不能直接解出d2x/dt2及其分量的显式表达式,为了能在不引入辅助矢量的条件下得到完整的六自由度模型,需对式(10)进一步处理,为此先对单位矢量进行求导运算。

2.1 单位矢量的求导

由于x是单位矢量,因此有:

x·x=1

(11)

地面坐标系下对式(11)两边求导,得到:

(12)

继续对式(12)两边求导,得到:

(13)

2.2 六自由度弹道矢量方程组的具体形式

以x点乘方程(10),得:

(14)

再以x×式(10),并考虑到:

(15)

得:

(16)

将式(13)代入式(16),得:

(17)

式(17)即为d2x/dt2的显式表达式,是矢量形式弹丸动量矩方程的另一种表示式。取式(9)、式(14)、式(17),它们构成了矢量形式六自由度弹道组的完整形式。

3 矢量形式六自由度弹道计算模型的分量表示与数值计算方法

将式(9)向地面坐标系投影,得地面坐标系下的分量方程组如下:

(18)

将式(17)向地面坐标系投影,得分量方程组如下:

(19)

设弹道上任一点的坐标为(X,Y,Z),则在地面坐标系中,dX/dt=V1,dY/dt=V2,dZ/dt=V3,联立式(14)、式(18)及式(19),并将方程组化为一阶常微分方程组,这样就能够用四阶R-K法或R-K-F方法[8]进行微分方程组的数值计算。

需要说明的是,由于数值计算误差的存在,计算过程中x3个分量x1、x2和x3积分值的平方和往往并不完全等于1,此时如果不对x的模修正,将会产生错误的计算结果。计算过程中归一化x的方法为:

(20)

4 弹道计算初始条件的确定

4.1 初始速度V0

设弹丸初速的高低角为θ0,初速的方向角为φ0,则弹丸初速V0在地面坐标系[1,2,3]上的分量为:

(21)

由于相对速度v=V-W,因此v0在地面坐标系[1,2,3]上的分量为:

(22)

4.2 初始单位向量x0

受起始扰动的影响,弹轴矢量x0与初速矢量V0可能出现不一致,设α0为初始高低扰动角,β0为初始方向扰动角,则x0在地面坐标系[1,2,3]上的分量为:

(23)

4.3 初始单位向量的一阶导数

1)y0和z0的确定

设y0_1、y0_2和y0_3为y0在地面坐标系[1,2,3]中的分量,由于y0在炮口处的铅直面内,又因为其垂直于x0,即y0·x0=0,因此可取y0_1=-x0_2,y0_2=x0_1,y0_3=0。于是:

(24)

根据z0=x0×y0,得z0在地面坐标系[1,2,3]上的分量为:

(25)

(26)

5 算例分析

下面根据文中的矢量形式六自由弹道模型,计算某炮不同起始扰动条件下弹道的射程X和侧偏Z。弹道计算的条件如下:标准气象条件,初速V0=930 m/s,射角θ0=45°,φ0=0°,起始扰动条件α0、β0、ωy、ωz及数值计算积分步长h见表1,计算结果如表1所列。作为对比,表1中同时列出了采用文献[4]中矢量形式六自由弹道模型及采用弹轴系欧拉角形式的六自由度弹道模型(参见文献[5])的计算结果。

从计算结果看,文中模型的计算结果与文献[4]中模型的计算结果及弹轴系欧拉角模型的计算结果是完全一致的。

表1 不同六自由度模型下计算结果比较

6 结论

参考文献:

[1] 唐成荣, 宋卫东, 许芹祖, 等. 某型激光未制导炮弹六自由度弹道仿真 [J]. 科学技术与工程, 2012, 10(26): 6453-6458.

[2] 闫章更, 祁载康. 射表技术 [M]. 北京: 国防工业出版社, 2000: 41-50.

[3] 李兴隆, 贾方秀, 王晓明, 等. 基于线性弹道模型的未段修正弹落点预测 [J]. 兵工学报, 2015, 36(7): 1188-1194.

[4] MCCOY ROBERT L. Modern exterior ballistics: the launch and dynamics of symmetric projectiles [M]. Atglen: Schiffer Publishing Ltd, 1999: 187-194.

[5] 韩子鹏. 弹箭外弹道学 [M]. 北京: 北京理工大学出版社, 2008: 132-143.

[6] 徐明友. 火箭外弹道学 [M]. 哈尔滨: 哈尔滨工业大学出版社, 2004.

[7] 中国华阴兵器试验中心. 兵器试验理论研究与实践: 闫章更学术讲座及论文选 [M]. 北京: 国防工业出版社, 2013: 74-85。

[8] 王兆胜. R-K-F方法在外弹道计算与火控系统中的应用 [J]. 数值计算与计算机应用, 2012, 33(1): 41-47.