破坏性测量与非破坏性测量相结合的火工品二元Wiener过程退化失效建模
王耀冬, 宣兆龙, 朱 宏, 俞卫博, 李翰朋
(1 解放军军械工程学院, 石家庄 050003; 2 西安现代控制技术研究所, 西安 710065)
0 引言
相对于火工品进行加速寿命试验来获取不多的失效数据评估可靠性,基于火工品性能退化数据的可靠性估计逐渐成为人们研究的重点。涂小珍[1]在双因素和恒定温度的单因素条件下,对某火工品进行了加速试验,通过计算试验后各性能指标的显著性变化,分析关键性能指标,并以此评估火工品的寿命;赵婉[2]通过分析爆炸螺栓性能退化数据随时间的变化趋势以及可靠性与退化数据的关系,间接得到可靠性与时间的关系曲线;麻宏亮[3]根据火工品不同时期关键性能参数的回归分析及容忍区间两方面,提出了基于趋势线分析的火工品寿命评估方法。可以看出,以上研究中评估火工品可靠性及寿命最后都归结为某一关键性能的变化,该性能到达了失效阈值,则火工品判为失效,进而评估可靠性。但是火工品的性能指标多样,各性能之间大多相互影响,且多数火工品的关键性能不止一个,若仅用单一性能的退化来评估可靠性,存在一定误差。
火工品作为一次作用的产品,一个样品只能检测一次获得一个或多个性能数据,测量之后即退出试验,因而获得的性能退化数据较少,同时,由于火工品个体之间的差异导致破坏性测量获得的退化数据具有一定波动性,可以通过增大样本量来减小这种波动,但必然增大工作量及成本,另一种方法可以通过Wiener过程[4]的独立增量性来解决。对于电火工品,其电阻可通过相应的电阻测试仪获得,一个样品可获得多个性能退化数据。但是文献[1,5]中指出,火工品在储存过程中,电阻随时间的退化过程非常缓慢,在可靠寿命及相当长一段时间内不会达到其失效阈值。结合火工品电阻以上特点,可将电阻与另一关键性能参数的退化数据联合建模,提高可靠性与寿命估计精度。因此,文中针对电火工品,通过对贮存或加速试验后的火工品进行破坏性与非破坏性检测相结合的方法获得性能退化数据,建立具有火工品相关性的二元Wiener过程的退化模型,并给出参数的估计方法,对火工品进行可靠性评估和寿命预测。
1 二元Wiener过程建模
1.1 模型选择
1)已知火工品为累积退化失效产品,其内装火工药剂和材料的失效都是由微小损失量逐渐累积造成的,符合Wiener过程建模要求,即产品的性能退化是由很多微小的损失量造成,且退化过程均匀平缓[4],因此,火工品的性能退化服从Wiener过程。
2)在一元Wiener过程中由于时刻t到t+Δt之间的变化量ΔX服从正态分布,因此ΔX可以大于、小于或等于0,即一元Wiener过程X(t)不是单调退化过程[7],由于火工品个体之间的差异导致破坏性测量获得的退化数据具有一定波动性,因此,Wiener过程适合火工品破坏性测量的性能退化建模。
3)由于火工品具有多个性能,且各性能之间具有一定的影响,因此,建立二元Wiener过程,即对两个具有相关性的一元Wiener过程进行联合建模。
对于电火工品,在已知电阻退化量不会超过其失效阈值的情况下,可以利用其与药剂之间的相关性,对火工品的威力、作用时间、点燃能力等通过破坏性测量获得的性能退化数据进行扩充,提高可靠性评估精度。
1.2 模型建立
记产品的性能参数分别为X和Y,假设其性能退化过程[X(t)Y(t)]′为二元Wiener过程,且在初始时刻X(0)=0,Y(0)=0,若X(0)≠0,只需令失效阈值为l-X(0)[8]。则由二元Wiener过程的性质可知,t时刻[X(t)Y(t)]′服从二维正态分布:
[X(t)Y(t)]′~N(tμ,tΣ)
(1)
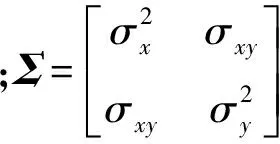
假设产品性能参数Y的退化趋势缓慢,其退化趋于而不会达到失效阈值,因此,仅考虑性能参数X,设失效阈值为l。由于性能参数Y可以进行多次非破坏性测量,得到多个时刻的性能退化数据,而性能参数X由于破坏性测量只能得到试验结束时刻的性能退化量,因此,一个产品在一次试验中可以获得一个性能退化数据X和多个性能退化数据Y。设产品i在恒定应力加速试验过程中,分别在时刻ti1,…,timi对性能参数Y进行mi次测量,而仅在时刻timi对性能参数X进行一次测量,timi即为加速试验中的定时截尾时间,此后产品i受到破坏退出试验。每个产品在试验中的测量过程都可以由图1表示。
对于性能参数Y,记相邻两次测量之间的时间间隔为Δtij=tij-ti(j-1),变化量为ΔY=Yij-Yi(j-1);对于性能参数X,虽然测量值仅为Ximi,但仍记变化量为ΔX=Xij-Xi(j-1),其中j=1,2,…,mi。由初始时刻性能退化量为0,得ΔXi1=Xi1,ΔYi1=Yi1。由二元Wiener过程的独立增量性,得[ΔXi1ΔYi1],…,[ΔYimiΔYimi]′相互独立且均服从二元正态分布[ΔXi1ΔYi1]′~N(Δti1μ,Δti1Σ),…,[ΔXimiΔYimi]′~N(Δtimiμ,ΔtimiΣ)。
记:C=[ΔXi1ΔYi1… ΔXimiΔYimi]′
(2)
则C服从维数为2mi的正态分布:
C~N(μC,ΣC)
(3)
式中:
μC=(Δti1μxΔti1μyΔti2μxΔti2μy…
ΔtimiμxΔtimiμy)′
调整C的顺序,令A=[ΔYi1ΔYi2… ΔYimiΔXi1ΔXi2… ΔXimi]′,则A也服从维数为2mi的正态分布:
A~N(μA,ΣA)
(4)
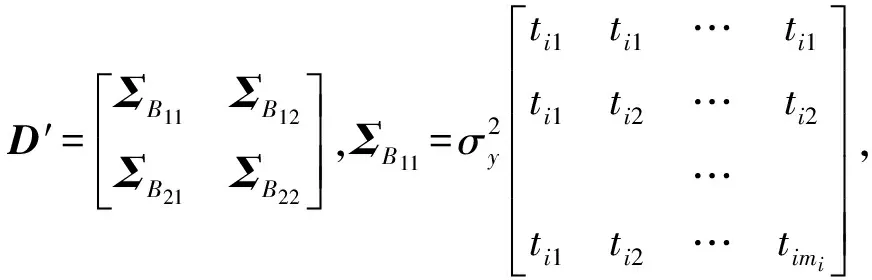
则:B~N(μB,ΣB)
(5)
2 参数估计

(6)
交换B中元素顺序,记W=[XimiYi1Yi2…Yim]′,可知W服从m+1维正态分布,W~N(μW,ΣW)。
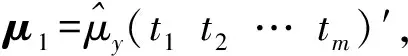
(7)
式中:
μXim=μxtm+ΣW12ΣW22(yi-μi)
(8)
记常数D,Ci(i=1,2,…,m)为:
(yi-μi)
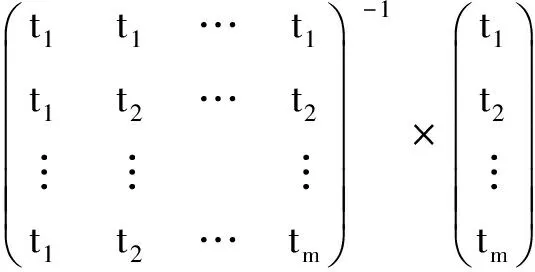
对数似然函数为:
(9)
(10)
3 剩余寿命预测
假设某产品在运行过程中在时刻t1,t2,…,tk测得其性能参数Y的值为Y1=y1,…,Yk=yk,由式(7)可知产品在tk的性能参数退化量Xk服从一元正态分布:
(11)
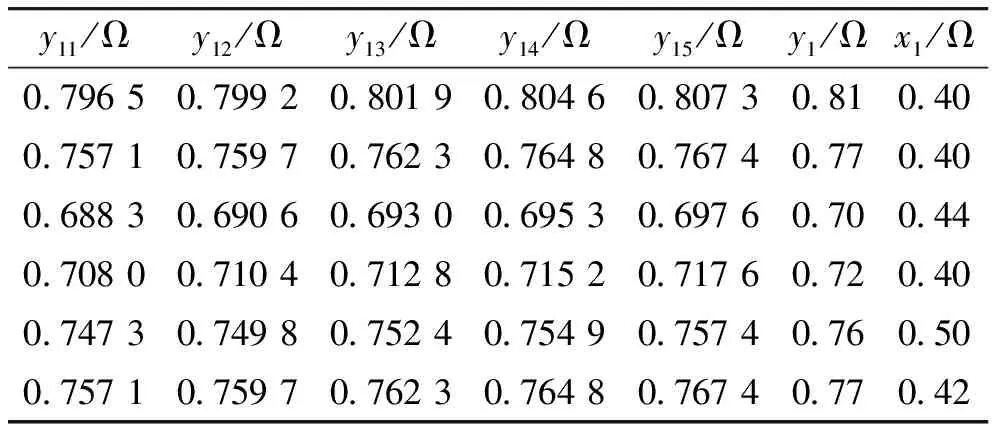
若到时刻tk产品仍未失效,设tk时刻性能参数退化量为xk(xk (12) 文献[2]对某库存电点火器进行了不同贮存时间的电阻及作用时间的性能检测,获得了一定数据,现以该电点火器为例运用以上方法进行可靠性评估及寿命预测。 该电点火器的技术指标为电阻(0.5~1.5 Ω),作用时间上限1 ms。由于文献[2]的检测方法一个产品只能获得一个电阻及一个作用时间的数据,与文中获得性能数据的方法不同,因此对试验数据进行以下改进: 设在检测时间ti测得第nij个火工品的电阻值为yij,需要在时间段(0ti)内生成k个电阻。文献[5]通过试验指出,随着电火工品老化其桥丝电阻缓慢增加,当增加2%以后则基本保持不变,即电阻增加速率逐渐递减。由于对数均匀分布估计法[10]可对区间内的数据进行估算,所得数据先密后疏,适合失效率随时间递减的产品,因此,可将这kr个电阻的对数均匀分布在[ln(0.98yij),lnyij]内,利用式(13)计算得到电阻yrm。 m=1,…,kr (13) 设k=5,应用MATLAB得到改进后的性能数据,在此仅列出第一个检测时间点即贮存13 a时6个电点火器样品电阻及作用时间的检测和改进数据,如表1所示。 表1 第一个检测时间电阻及作用时间的检测和改进数据 利用文中提出的方法进行估计,得到: 则该火工品的寿命分布密度函数为: (14) 通过以上分析可以看出,文中提出的破坏性测量与非破坏性测量相结合的方法扩大了获取性能退化数据的信息量,对于电火工品具有很强的实用性,建立的二元Wiener过程退化失效模型考虑了性能之间的相关性,能够得到火工品退化失效分布及剩余寿命概率分布,与只以单一性能退化数据或多种性能退化散布估计火工品可靠性及寿命的方法相比,通用性更强,不局限于某型火工品,获得寿命评估数据更全面,为火工品可靠性评估和寿命预测提供了新的思路。 参考文献: [1] 涂小珍, 李敬明, 韦兴文, 等. 某火工品贮存老化效应分析研究 [J]. 含能材料, 2008, 16(5): 539-542. [2] 赵婉, 杨静. 基于性能退化数据评价火工品贮存可靠性的方法 [J]. 含能材料, 2012, 20(4): 406-408. [3] 麻宏亮, 张蕊, 李芳, 等. 趋势分析方法在火工品寿命评估中的应用 [J]. 火工品, 2013(3): 53-56. [4] 彭宝华. 基于Wiener过程的可靠性建模方法研究 [D]. 长沙: 国防科学技术大学, 2012. [5] 陈明华. 加速老化对电火工品电阻与发火时间的影响 [J]. 火工品, 2008(5): 37-38. [6] 周彬. 桥丝式电火工品瞬态脉冲无损检测技术研究 [D]. 南京: 南京理工大学, 2004. [7] 孙权, 冯静, 潘正强. 基于性能退化的长寿命产品寿命预测技术 [M]. 北京: 科学出版社, 2015: 33-36. [8] 王小林. 基于非线性Wiener过程的产品退化建模与剩余寿命预测研究 [D]. 长沙: 国防科学技术大学, 2016. [9] WHITMORE G A. Estimating degradation by a wiener diffusion process subject to measurement error [J]. Lifetime Data Analysis, 1995, 1(3): 307-319. [10] 茆诗松, 王玲玲. 加速寿命试验 [M]. 北京: 科学出版社, 1997: 26-28.4 实例分析
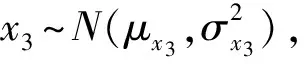
5 结论

