基于序列近似优化算法的固体运载火箭弹道设计
彭 科,胡 凡,张为华
(国防科学技术大学 航天科学与工程学院,长沙 410073)
基于序列近似优化算法的固体运载火箭弹道设计
彭 科,胡 凡,张为华
(国防科学技术大学 航天科学与工程学院,长沙 410073)
采用打靶法研究固体运载火箭弹道优化设计问题。针对打靶法中智能优化算法效率、优化问题中约束条件提法等方面的不足,引入序列近似优化算法,提出算法中径向基函数高斯核宽度的高效确定方法。数值仿真实验表明,提出的方法可在基本不带来计算量增加的前提下,显著提高代理模型精度,使序列近似优化算法得到改进,提高优化效率。设计固体运载火箭飞行程序。建立弹道优化设计问题数学模型,并将模型中相关等式约束合理转化为不等式约束,降低优化问题求解难度;基于改进后的序列近似优化算法完成某固体运载火箭弹道优化,原始计算模型调用308次之后便搜索到最优解,较传统智能优化算法显著提高了优化效率,优化方案末助推级液体推进剂消耗比原方案减少25.7%。
固体运载火箭;弹道优化;打靶法;序列近似优化;径向基函数;高斯核宽度
0 引言
固体运载火箭具有响应速度快、机动性强、成本低、可靠性高的特点,是各国研制的热点[1]。运载能力是火箭发射最大有效载荷的能力,是描述运载火箭性能的关键指标[1]。固体火箭运载能力相对较小,运载能力受飞行弹道影响较大,开展弹道优化设计研究对提高其运载能力和降低发射成本具有重要意义[2]。
运载火箭弹道优化是一类终端时刻自由、终端状态固定且带有路径约束的多阶段、非线性最优控制问题[3],求解该问题的数值方法一般分为间接法和直接法[4]。间接法存在收敛域小、难以估计共轭变量初值等不足,且推导过程较为复杂[3];直接法采用参数化方法,将连续空间的最优控制问题转化为非线性规划问题进行数值求解,在飞行器弹道优化领域得到广泛应用[4]。根据参数化方法不同,直接法可分为同时离散控制变量和状态变量的配点法[5]和仅离散控制变量的打靶法,配点法难以保证获得的解是原最优控制问题的解[4]。本文采用打靶法完成固体运载火箭弹道优化。
固体运载火箭弹道优化问题存在多个不等式约束和等式约束,对打靶法中优化算法的全局寻优能力和精度提出严峻挑战。已有研究中主要采用智能优化算法[6-7]、智能优化与局部寻优结合的算法[8-9]、智能优化与非线性方程组迭代求解方法结合的算法[10-12]。现有优化方法在减少计算量、提高全局优化能力、减轻对优化初值依赖等方面尚有较大改进空间。序列近似优化算法(Sequential Approximate Optimization,SAO)基于少量初始采样点构造初始代理模型,采取一定的加点策略更新采样点,逐步提高代理模型对最优解的近似精度,根据收敛准则终止算法并输出最优解[13-15]。相比智能优化算法,SAO算法可在保证全局最优的前提下大幅降低原模型调用次数,显著提高优化效率[14]。代理模型构造是SAO算法的关键技术,提高其精度对改善SAO算法效率具有显著作用[16]。代理模型构造基本思想是在一定的精度条件下,用一个相对简单的逼近函数近似替代复杂高精度性能分析模型,利用已知点(样本)的响应信息来预测未知点响应值,国内外学者对代理模型相关方法进行了大量研究[13, 17-19]。径向基函数在精度和鲁棒性方面皆较为可靠[20],是SAO算法中被广泛使用的代理模型,其核宽度的合理确定对近似精度有决定性影响。文献[13]提出了一种采样点个数趋于无穷情况下的非均匀核宽度确定方法;文献[14]提出了基于采样点局部密度的核宽度确定方法,但算法中总影响体积这一关键参数依赖经验确定,难以实现最优的近似精度;文献[18]解决了采样点较为均匀条件下的径向基函数核宽度确定问题。序列近似优化过程中样本点数量由少逐渐增多,样本分布较不均匀,建立不同规模、非均匀样本的径向基函数(radial basis function, RBF)核宽度确定方法,对提高序列近似优化过程代理模型精度、提高优化效率具有重要意义。此外,运载火箭弹道优化问题中等式约束的存在使得可行域范围较小,往往需要对等式约束进行特殊处理,处理策略尚无一般规则,是一个有待研究的难题[6]。将等式约束转化为不等式约束,从而改进优化问题描述方式,可显著利于运载火箭弹道优化问题的求解。
针对现有弹道优化方法的不足,引入SAO算法,提出算法中径向基函数高斯核宽度的高效确定方法,提高代理模型精度;设计固体运载火箭飞行程序;构建弹道优化设计问题数学模型,并将其中相关等式约束合理转化为不等式约束,降低优化问题求解难度;基于SAO算法完成某固体运载火箭弹道优化,并分析结果。
1 序列近似优化算法及其改进
为方便讨论,给出一般优化问题的数学表述:
(1)
本文SAO算法的流程如图1所示[14],主要步骤:(1)采用式(2)将设计空间线性映射到n维单位立方体内,采用拉丁超立方法得到初始采样点,并计算初始采样点目标函数与约束值;(2)基于径向基函数构建目标函数与各约束值的代理模型;(3)基于代理模型,采用自适应采样策略更新样本点;(4)收敛判断。
(2)
式中XiU、XiL分别为第i维设计变量的上下界;Xi、xi分别为原设计空间与映射后单位立方体中第i维设计变量的取值。
样本点更新的自适应采样策略取文献[21]中的方法,该策略通过求解以下优化问题实现,将最优解作为新采样点加入样本中。
(3)
(4)
(i,j=1,2,…,N,i≠j)
(5)
式中N为采样点个数;xi、xj为样本点的坐标。
采样初期样本点较少,δ数值较大,使得新采样点向未知区域探索,随着样本点数量的逐渐增多,δ数值逐渐减小,逐渐趋向最优区域搜索,即采用式(5)所示的最小距离约束可使得根据优化问题(3)得到的新采样点具有自适应特性[21]。
本文采用粒子群算法求解式(3)所示优化问题,收敛判断准则采用文献[14]中的方法。提出新的径向基函数核宽度确定方法,提高代理模型精度,改进SAO算法,提高优化效率。
给定N个训练样本S:[xi,yi](i=1,2,…,N),基本径向基函数的数学模型为[22]:
(6)
式中x为设计变量向量;xi是第i个样本点的位置向量;ri=x-xi为欧式距离;wi为第i个基函数的权系数;φ为基函数。
本文取基函数为Gauss函数,即:
(7)
式中σi为第i个基函数的核宽度。
将N个训练样本代入式(6),即得包含N个未知数wi(i=1,2,…,N)的N维线性方程组,求解该方程组即可求得基函数的权系数wi,本文采用QR分解法求解。
式(7)中基函数核宽度σi的确定对代理模型预测精度有决定性影响,文献[14]提出了基于样本点局部密度并估计总影响体积的核宽度σi计算方法,局部密度定义如下:
(8)
其中
(9)
文献[14]中,总影响体积这一关键参数较难确定,难以实现较优的核宽度估计。本文在样本点局部密度计算的基础上,提出新的核宽度确定方法。
核宽度σi表征了第i个样本点影响区域的大小[14],σi的n次方应与密度函数ρ(xi)成反比,即
(10)
式(10)包含N-1个独立的方程,待解的核宽度σi为N个,求得任意样本点核宽度后即可求解其余样本点的核宽度。
考虑局部密度最小的样本点xs,设其核宽度为σs,其基函数在距xs最近的样本点的数值为
(11)
若σs数值过小,其余样本点的核宽度σi也将过小,将导致径向基函数代理模型不光滑;反之若σs数值过大,将导致龙格现象。合理的σs取值应保证样本点xs的基函数的影响域应到达离其最近的样本点的位置,即φ(ds,min)的数值应足够大,φ(ds,min)与σs/ds,min的数值关系如图2所示。
当σs/ds,min<0.659 2时,φ(ds,min)<0.1,数值偏小,即样本点xs的影响偏弱;当σs/ds,min>1时,φ(ds,min)>0.376 9。本文取σs/ds,min=1,以保证样本点xs的影响域到达离其最近的样本点,确保代理模型光滑,即
σs=ds,min
(12)
由式(10)与式(12)得,各样本点核宽度σi(i=1,2,…,N)计算如下:
(13)
采用下式准则比较本文提出的核宽度确定方法和文献[13]与文献[23]提出的方法对应径向基函数的近似精度:
(14)

R2≤1,越接近于1表明近似模型精度越高;R2=1时表明近似模型在验证样本处的误差为0。
取如下所示5个典型测试函数。
函数I(一维函数):
f(x)=xsin(1.5x),0≤x≤10
函数II(低维低阶函数):
f(x)= sin(x1+x2)+(x1-x2)2-1.5x1+
2.5x2+1,|xi|≤5
f(x)= (10+x1cosx1)×[3+exp(-x22)],
|xi|≤5
函数IV(高维低阶函数):
f(x)= 2(x1-1)2+x22-x1x2+(4-x3)2+3(x4-6)2+
0.5(x5-2)2+(x6-10)2+4(x7-9)2+
2(x8-5)2+33,|xi|≤20
函数V(高维高阶函数):
|xi|≤4
采用文献[24]的方法,验证本文提出的核宽度确定方法的性能,函数I取10个随机样本点,函数II、III取50个随机样本点,函数IV、V取200个随机样本点,根据3种核宽度确定方法建立近似模型,为保证近似精度R2计算的准确性,取足够多的验证样本点,数量为1 000,进行20次独立的随机数值仿真实验,计算R2与R2的平均值MR2。3种核宽度确定方法的MR2值比较如图3所示。结果表明,本文方法近似精度显著优于其他2种方法,可改善SAO算法效率和精度。
2 固体运载火箭总体参数与飞行程序设计
2.1 总体参数
适宜气候:温暖湿润;年均气温10~20 ℃,1月份平均气温3~9 ℃,7月份平均气温24~28 ℃,极端最高气温低于35 ℃,极端最低气温高于0 ℃,年均降水量600~1 200 mm,年平均日照600~1 200 h[7]。
本文研究的固体运载火箭由三级固体发动机与液体末助推级组成,各级固体发动机参数性能参数如表1所示。末助推级液体推进剂质量为230 kg,真空比冲Isp=2 850 N·s/kg,真空推力Tb=2 000 N。全箭最大直径为1.4 m,目标轨道为300 km太阳同步圆轨道,入轨质量约450 kg。
2.2 飞行程序设计
本文固体运载火箭采用直接入轨方式,飞行过程一级动力飞行段、一级滑行段、二级动力飞行段、二级滑行段、三级动力飞行段、三级滑行段、末助推段等7个阶段[8],飞行程序如下:
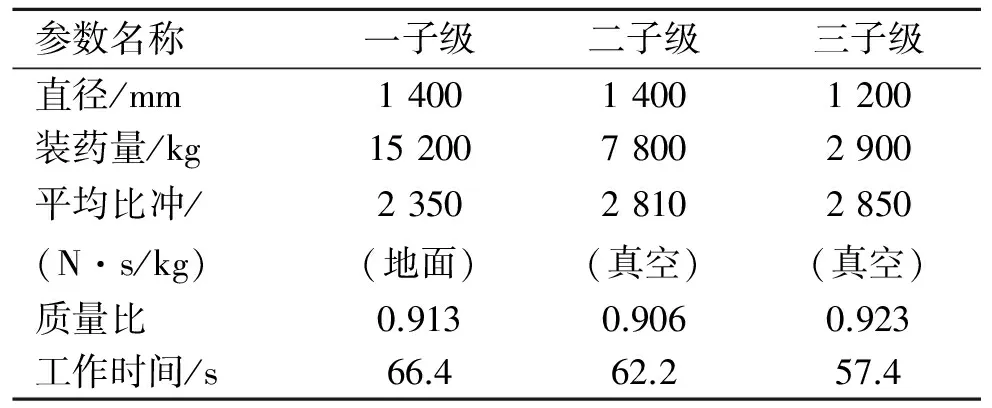
参数名称一子级二子级三子级直径/mm140014001200装药量/kg1520078002900平均比冲/(N·s/kg)2350(地面)2810(真空)2850(真空)质量比0.9130.9060.923工作时间/s66.462.257.4
(1)一级飞行段
运载火箭一级在稠密大气层中飞行,火箭垂直起飞,而后按攻角程序转弯,飞行速度进入跨声速前结束转弯[25],而后保持零攻角飞行,飞行程序为
(15)
其中
α(t)=-αmsin2f(t),t1 (16) (17) 为便于处理,引入λm=(tm-t1)/(t2-t1)。 (2)二级飞行段 运载火箭真空飞行动力段最优俯仰角程序近似为线性[25]: (18) 运载火箭二级及以上飞行段大气已较稀薄,飞行程序按真空飞行段设计[25]: (19) (3)三级飞行段 运载火箭三级飞行段飞行程序设计: (20) (4)末助推段 末助推段飞行程序设计: 末助推关机时刻应达到入轨条件。 3.1 设计变量 根据飞行程序,取固体运载火箭弹道优化设计变量为 x=[x1x2x3x4x5x6x7x8x9x10x11x12x13]T (22) 式中A0为发射方位角。 本文取设计变量上下限如表2所示。 表2 固体运载火箭弹道优化设计变量上下限 3.2 目标函数 本文弹道优化设计问题目标函数的实质是燃料消耗最省。由于助推系统三级固体发动机均采用耗尽关机工作模式,选取末助推级消耗液体推进剂质量mp最小作为目标函数[3],即 (23) 3.3 约束条件 本文弹道优化设计问题约束条件包括不等式约束和等式约束。为保证火箭安全飞行,对法向过载ny、一级程序转弯结束时马赫数Mat2与一二级分离时动压qsep进行约束,得如下所示不等式约束: (24) 式中nymax为法向过载上限值,nymax=0.05;Mat2max为一级程序转弯结束时马赫数上限值,Mat2max=0.75;qsepmax为一二级分离时动压上限值,qsepmax=10 kPa。 目标轨道为300 km太阳同步圆轨道,得等式约束: (25) 式中h、v、e、i分别为实际入轨高度、入轨速度、偏心率和轨道倾角;hobj=300 km、vobj=7 725.84 m/s、eobj=0、iobj=96.67°分别为目标轨道高度、速度、偏心率和轨道倾角。 式(25)中轨道倾角i主要受设计变量中发射方位角A0影响,优化过程中Ceq4(x)较易满足。Ceq1(x)、Ceq2(x)、Ceq3(x)对大多数设计变量敏感,优化过程难以满足,约束条件的处理难度较大,优化问题难以求得全局最优解。 本文建立的运载火箭弹道优化问题不考虑式(25)中Ceq1(x)、Ceq2(x)、Ceq3(x)等3个等式约束。根据末助推关机点参数计算出轨道近地点高度hp,以hp≥hobj=300 km为约束,因目标函数为燃料消耗最省,优化问题的最优解必然为300 km圆轨道,即满足式(25)中的Ceq1(x)、Ceq2(x)、Ceq3(x)等3个等式约束。得本文运载火箭弹道优化问题约束条件如下: (26) 采用改进后的SAO算法,优化过程弹道计算采用发射系中空间三自由度弹道方程,具体计算模型见文献[25]。取初始样本点为200个,优化过程目标函数收敛曲线如图4所示,迭代至第108步,原始计算模型调用308次之后,便搜索到全局最优解,较传统智能优化算法上万次的原始计算模型调用次数[6],显著提高了优化效率。 优化后弹道与优化前的原始弹道设计变量与性能参数的对比如表3、表4。其中,原始弹道为人工调节得到的弹道方案。优化方案末助推级液体推进剂消耗量为147.62 kg,比原始方案减少25.7%,各项设计指标与约束满足要求。优化弹道高度、速度、动压、俯仰角、当地速度倾角随时间变化曲线如图5、图6所示。 表3 固体运载火箭弹道优化方案与原方案设计变量数值 表4 固体运载火箭弹道优化方案与原方案对应特征参数 (1)提出了巧妙、高效、可靠的径向基函数高斯核宽度的确定方法。基于样本点局部密度计算结果,合理确定局部密度最小的样本点基函数核宽度,进而巧妙地确定其他样本点的核宽度。提出的核宽度确定方法在基本不带来计算量增加的前提下,显著提高了代理模型精度。 (2)设计了固体运载火箭飞行程序。建立了弹道优化设计问题数学模型,并将模型中与入轨点高度、速度、当地速度倾角关联的3个等式约束合理转化为与轨道近地点高度关联的1个不等式约束,降低了优化问题求解难度。 (3)基于改进后的SAO算法,完成了某固体运载火箭弹道优化,原始计算模型调用308次之后,便搜索到最优解,较传统智能优化算法显著提高了优化效率。优化方案各项指标与约束满足设计要求,末助推级液体推进剂消耗比原方案减少25.7%。 [1] 洪蓓, 梁欣欣, 辛万青. 固体运载火箭多约束弹道优化[J]. 导弹与航天运载技术, 2012(3): 1-5. [2] 龙乐豪.总体设计(上)[M].北京:宇航出版社,1989. [3] 杨希祥, 张为华. 基于Gauss伪谱法的固体运载火箭上升段轨迹快速优化研究[J]. 宇航学报, 2011, 31(1): 15-21.[4] 雍恩米, 陈磊, 唐国金. 飞行器轨迹优化数值方法综述[J]. 宇航学报, 2008, 29(2): 397-406. [5] 龚春林, 韩璐. RBCC可重复使用运载器上升段轨迹优化设计[J]. 固体火箭技术, 2012, 35(3): 290-295. [6] 杨希祥, 江振宇, 张为华. 基于粒子群算法的固体运载火箭上升段弹道优化设计研究[J]. 宇航学报, 2010, 31(5): 1304-1309. [7] 李振华, 鲜勇, 雷刚, 等. 基于混合粒子群算法的上升段交会弹道快速优化设计[J]. 航空动力学报, 2015, 30(12): 3029-3034. [8] 杨希祥, 张为华, 肖飞, 等. 小型固体运载火箭运载能力分析[J]. 固体火箭技术, 2009, 32(4): 355-359. [9] Volker Maiwald. About combining tisserand graph gravity-assist sequencing with low-thrust trajectory optimization[C]//International Conference on Astrodynamics Tools and Techniques, Darmstadt: 2016. [10] 崔乃刚, 黄盘兴, 路菲, 等. 基于混合优化的运载器大气层内上升段轨迹快速规划方法[J]. 航空学报, 2015, 36(6): 1915-1923. [11] 黄文博, 张强, 肖飞, 等. 空间快速响应航天器轨道/弹道一体化规划[J]. 固体火箭技术, 2012, 35(1): 11-16. [12] Abolfazl Shirazi. Trajectory optimization of spacecraft high-thrust orbit transfer using a modified evolutionary algorithm[J]. Engineering Optimization,2015: 1-19. http://dx.doi.org/10.1080/0305215X.2015.1115026. [13] Kitayama S,Arakawa M,Yamazaki K.Sequential approximate optimization using radial basis function network for engineering optimization[J]. Optimization and Engineering,2011, 12: 535-557. [14] Wang D H,Wu Z P,Fei Y,et al. Structural design employing a sequential approximation optimization approach[J]. Computers and Structures,2014, 134: 75-87. [15] Kitayama S, Arakawa M, Yamazaki K. Sequential approximate optimization for discrete design variable problems using radial basis function network[J]. Applied Mathematics and Computation,2012, 219(8): 4143-4156. [16] Jacobs J H,Etman L F P,Keulen F Van,et al. Framework for sequential approximate optimization[J]. Structural And Multidisciplinary Optimization,2004, 27: 384-400. [17] Deng Y M,Lam I C,Tor S B. A CAD-CAE integrated injection molding design system[J]. Eng. Computation,2002, 18: 80-92. [18] Kitayama S,Yamazaki K. Simple estimate of the width in Gaussian kernel with adaptive scaling technique[J]. Applied Soft Computing,2011, 11: 4726-4737. [19] Luo C,Zhang S,Wang C. A meta model-assisted evolutionary algorithm for expensive optimization[J]. Journal of Computational and Applied Mathematics,2011, 236: 759-764. [20] Jin R,Chen W,Simpson W T. Comparative studies of metamodeling techniques under multiple modeling criteria[J]. Journal of Structural and Multidisciplinary Optimization,2001, 23: 1-13. [21] 武泽平, 王东辉, 杨希祥,等. 基于径向基代理模型的序列优化中自适应再采样策略[J]. 国防科技大学学报, 2014, 36(6): 18-24. [22] Hardy R L. Multiquadratic equations of topography and other irregular surfaces[J]. Journal of Geophysical Research,1971, 76: 1905-1915. [23] Nakayama H,Arakawa M,Sasaki R. Simulation-based optimization using computational intelligence[J]. Optimization and Engineering,2002(3): 201-214. [24] Wang Dong-hui,Hu Fan,Ma Zhen-yu, et al. A CAD/CAE integrated framework for structural design optimization using sequential approximation optimization[J]. Advances in Engineering Software,2014, 76: 56-68. [25] 陈克俊, 刘鲁华, 孟云鹤. 远程火箭飞行动力学与制导[M]. 北京: 国防工业出版社, 2014. (编辑:吕耀辉) Solid launch vehicles trajectory design based on sequential approximate optimization algorithm PENG Ke, HU Fan, ZHANG Wei-hua (College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China) Solid launch vehicles trajectory optimization problem was researched using shooting method. Current shooting methods have shortcomings on the efficiency of intelligent optimization algorithms and constraints formulation. The sequential approximate optimization (SAO) algorithm was introduced to solve solid launch vehicles trajectory optimization problem. A high efficiency Gaussian kernel width determining method for radial basis function (RBF) used in SAO was proposed. Numerical experiments show that the proposed kernel width determining method improves the approximate accuracy of RBF remarkably and generates almost no excessive calculation cost. Flight program and trajectory optimization problem for solid launch vehicles were established. In order to reduce the difficulty of solving solid launch vehicles trajectory optimization problem, equality constraints in optimization problem were transformed into an inequality constraint ingeniously. Based on improved SAO algorithm, trajectory optimization for a launch vehicle was accomplished, and the global optimal solution was obtained after calculating original model 308 times. Propellant consumption of the upstage in optimization scheme is 25.7% less than primary scheme. solid launch vehicle;trajectory optimization;shooting method;sequential approximate optimization;radial basis function;Gaussian kernel width 2016-01-27; 2016-04-20。 彭科(1989—),男,博士生,研究方向为飞行器总体设计优化。E-mail:pengke_pk@163.com 张为华,男,教授,博士生导师,研究方向为飞行器总体设计。E-mail:zhangweihua@nudt.edu.cn V412.1 A 1006-2793(2017)02-0250-07 10.7673/j.issn.1006-2793.2017.02.021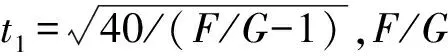
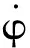



3 弹道优化设计问题数学模型

4 优化结果与分析


5 结论

