金融泡沫与过度自信模型

方灿琦

金融泡沫与过度自信模型

方灿琦

过度自信模型通过投资者过度自信解释了的金融泡沫形成，但存在一些局限性。为了弥补和充实该模型研究的薄弱之处，本文依照实际经济环境中，不限投资者数量，并考虑所有投资者的信息，推导出N维过度自信模型。在这基础上，本文得出对单位资产价格定价模型。定价模型中的递归结构意味着投标者不仅将获得资产，而且还将获得再售期权。投标者愿意支付比其评估资产的基本价值更高的价格，超额部分是再售期权的价值，这也被定义为过度自信泡沫。

金融泡沫；过度自信；再售期权

一项资产的股权，不仅意味着可以获得相关的分红，而且还可以通过出售资产，从别人手里获得对未来的股价和股息支付高估的盈利机会。当股价与股票内在价值大幅偏离时，就会出现金融泡沫。在近现代世界经济史上，金融泡沫出现了许多次，如郁金香，南海泡沫和大萧条，被称为“三大著名投机风潮”。金融泡沫主要就是经济上的宏观调空不当，过度的投资引起资产价格的过度膨胀，盲目追求经济增长，导致虚假繁荣的一种假象，引发社会经济混乱。

Scheinkman和Xiong（2003）在所创建的二维金融泡沫均衡模型中，认为股票投资者具备异质信念，在卖空机制缺失的条件下，异质性会促使连续交易的行为，增加换手率，容易引起股票市场价格单方向偏离股票的内在价值，加速泡沫的形成。本文在此基础上考虑所有投资者，和所有投资者的信息，推导出更为符合实际情况的N维过度自信模型。

一、文献综述

目前，国外有许多优秀的学者建立了一些经典模型，说明金融泡沫的形成机理。Shiller等人（1984）认为股票价格受到社会运动和时尚潮流的影响。投资者高度关注彼此可能会导致泡沫。De Long等人（1988）用噪声交易者构建了一个投资组合模型，他们对期望收益有不正确的信念。噪声交易者可以获得比理性交易者更高的预期收益，同时，他们的行为会引起系统风险的增加。De Long等人（1990）也提出了一个积极的反馈模型。噪音交易者遵循正反馈策略，当价格上涨时买入资产，当价格下跌时卖出。当理性投机者收到好消息时，他们意识到最初的价格上涨将吸引正反馈交易者购买。当他们意识到这种交易时，理性交易者将在当前时间购买大量的这种资产，使得价格高于内在价值。然后，正反馈交易者对价格的上涨做出反应，从而使价格偏离基本面。Topol（1991）提出了一个模型，他认为个人投资者和集体意见可能存在的市场。他描述了一种情况，交易者知道他们有不完整的信息。基于缺乏完整的信息，和最近的买家和卖家的平均价格，投资者进行评估给出他们的价格。泡沫发生和价格波动增加会随着投资者的模仿行为增加而增加。

在诸多研究中，有一部分学者专门针对过度自信进行研究。过度自信的个人会高估他所收到的信息的精确度。Allen和Evans（2005）考虑实证竞价数据，发现约40%的受试者表现出过度自信。还特别发现，经验丰富不会减少过度自信程度。Miler（1977）解释，不确定性和风险影响不同的信念，这将导致资产在一个市场很少或没有高估而卖空的机会。Harrison and Kreps（1978）考虑了一个简单的金融泡沫模型，为了以更高的价格卖给对未来股票价值有信心的其他投资者，投资者购买股票。Scheinkman和Xiong（2003）提出了基于投资者过度自信产生的异质信念，一种资产交易模型，其均衡是广泛适用的。这个模型可以看作是Harrison和Kreps的论文中完整的框架。他们认为投资者可能存在过度自信，并且准备在未来以更高的价格出售所持有的资产。投资者的这种行为很大程度上会引发金融泡沫的发生。

在本文中，根据Scheinkman和Xiong（2003）的基本模型，构建一个资产交易模型。在模型中，不考虑大于两个的风险中性投资者小组，而是假设每个小组都有一个独立的信号。所有投资者都可以观察到其他投资者的信号。从每组信号的信息的高估，可以得到N个条件均值信念集合和N×N异质信念矩阵。在未来某个时间里，较乐观的投资小组可能变得不如其他投资小组乐观，其预测平均波动将产生交易。在卖空受限的条件下，资产所有者有权将资产出售给那些更为乐观，且能支付交易成本的投资者，如托宾税。再售期权具有递归结构，这意味着下一个成功的投标人将同时获得资产和再售期权。因此，买方支付的价格高于其对资产内在价值的估值。该超额部分是再售期权的价值，同时也被定义为资产泡沫。从模型可以看出，即使信用差异很小，足够的交易量也会导致可见的资产泡沫。泡沫的出现总是伴随着高交易量和高价格波动。

二、模型推导

Scheinkman和Xiong（2003）的模型是针对具有有限供给的风险资产和有限数量投资者的单一风险资产的连续时间模型。其中，这些投资者被分为两组，组A和B。与f相关的资产的当前股利和两个信号然可以通过投资者小组观察到，其中，投资者对信号中获得的信息的过度相信会产生对未来股息不同的预测。

本文模型遵循Scheinkman和Xiong的基本观点。他们构建了一个考虑红利的单一风险资产的模型，由两个参数组成，一个是不可观察的基本变量f，另一个是噪声。因此，可得出累计红利Dt，如下：

其中ZD是标准布朗运动①布朗运动是随机运动。当流体中随机分布的流体中悬浮的颗粒移动不规则时，它们将具有不规则运动，称为布朗运动。，σD＞0是恒定波动率参数，t是时间。假设基本变量f不可观察，但满足随机过程，

其中λ≥0是平均反转参数，f是f的长期均值，σf＞0是恒定波动参数，Zf是标准布朗运动。

不同于Scheinkman和Xiong（2003），本文将风险中性投资者分成N组，x（ii=1，...，N）。除了累计红利外，所有投资者观察得到一组信号向量并满足下式：

在组xi(i=1,2,…,N)中的投资者将作为自己的信号，同时他们也可以观察其他人的信号。当来自投资者表达的信号的信息量大于真实的信息量时，可能会出现投资者的异质信念。因此，在这里，假设组xi中的投资者认为在信号中的噪声和在（2）式中的噪声dZf相关，其中φ定义为0＜φ＜1。在（3）式中，投资者xi认为的信号满足，

投资者虽然获得了信号的正确的波动情况，但是由于两个噪声之间存在相关性，这引起了投资者对信号的过度反应。

三、过滤问题

由于所有的噪声都是正态分布，因此可以通过减少过滤问题，得到投资者信念的条件均值和方差。根据正态分布条件，投资者小组为I∈x1,x2,…,xn，投资者小组的信念满足条件均值fI和条件方差的平稳偏差γI的正态分布。根据在Liptser和Shiryaev（1978）书中的定理12.7，可以获得条件方差γI之前的平稳解和条件均值fI的演化。

条件方差的平稳解是：

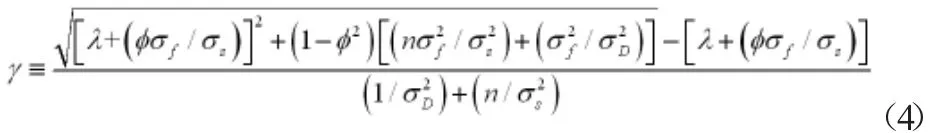
让u(φ)=λ+(φσf/σs),v(φ)=(1－φ2)[(nσf2/σs2)+(σf2/σD2)]

将u和v代入（4）式得

γ关于φ求导得

由于σD,σf,σs＞0,0＜φ＜1和λ≥0

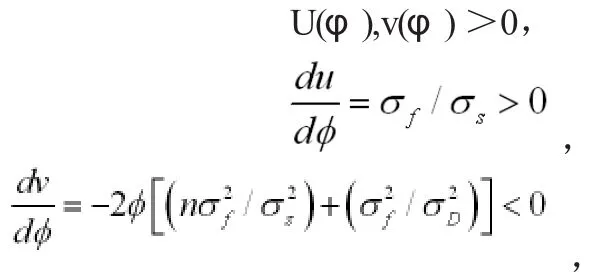
因此，

在（6）式中，条件稳定方差γ随着参数φ的增加而减小，因此，（6）式表明了参数φ与过度自信有关。

通过Liptser和Shiryaev（1978）0书中的定理12.7，可推导出来投资者条件均值在组xi中的演化，如下：

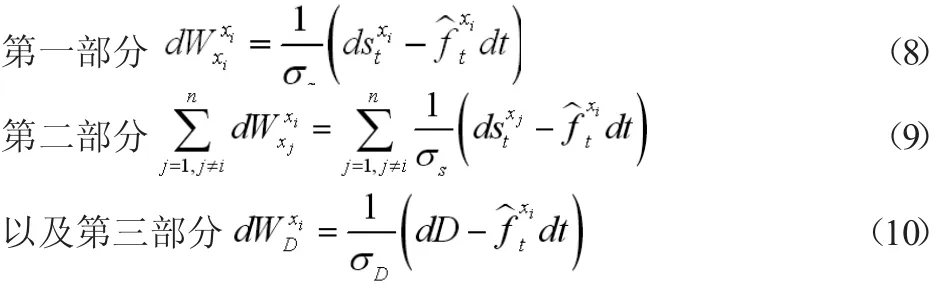
根据以上内容，本文将组xi中投资者信念的条件均值称为，简称为信念。

四、异质信念的演变

设投资者小组xi和xj的异质信念矩阵。

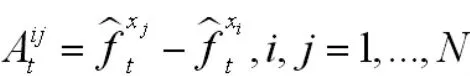
然后，给出方程来表达异质信念的变化

直接带入（7）式，得

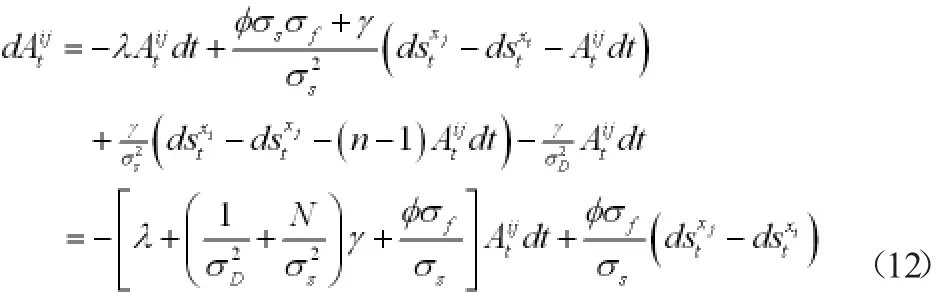
通过（4）式定义Atij的平均反转参数ρ为

将（12*），（8）和（9）式代入（12）式

得WAxi=Wxjxi－Wxixi，

那么，可以证明，对于组xi的投资者来说，对组xi的创新与中的创新是正交的。

该方程可以被写成

其中σA=φσf，

且WAxi是组xi中的投资者的标准布朗运动。（13）式意味着异质信念Atij遵循投资者组xi的均值回归的扩散过程。异质信念的波动为零，即不存在过度自信（φ=0），并且异性信念随着φ的增加而增加。因此，－ρ/2σA2测量到原点的拉力，Conley（1997）0认为这是均值回复的正确度量。

五、单位资产定价

投资者的异质信念的差异引起交易的产生。出于对未来股价和股息支付的高估，投资者将对该资产竞价。此外，假设卖方为每单位已售资产支付交易成本c≥0（例如交易费用，如托宾税等）。

假设组xi中的投资者愿意每单位资产支付ptxi。由于假设有限数量的资产和数量无限的潜在买家的卖空限制，最终完成交易的买方将支付其保留价值。投资者的保留价格①保留价格是指买方所能接受的最高价格或卖方所能接受的最低价格。可以反映他对资产的估值以及在其他投资者组中未来销售价格的利润。

设x0∈{xi}为当前资产所有者小组，是其他组，Etx0是组x0的所有者的期望，以及在t时间他们获得信息，因此单位风险资产的价格是

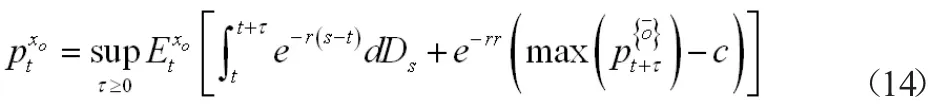
其中R是未来贴现收益率（假设每个投资者可以贷入借出相同的收益率），τ是停止时间，pxit+τ是组xi在t+τ时间买方保留价格，意味着在t+τ时间其他组的投资者出售资产获得的利润。

根据（1）式，可得

因此，将（7）代入（15）中，得

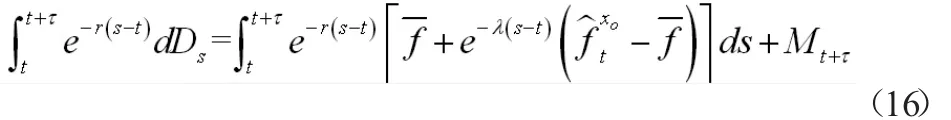
其中Etx0(Mt+τ)=0。根据（16），（14）式可以表示为

（17）式积分整理得

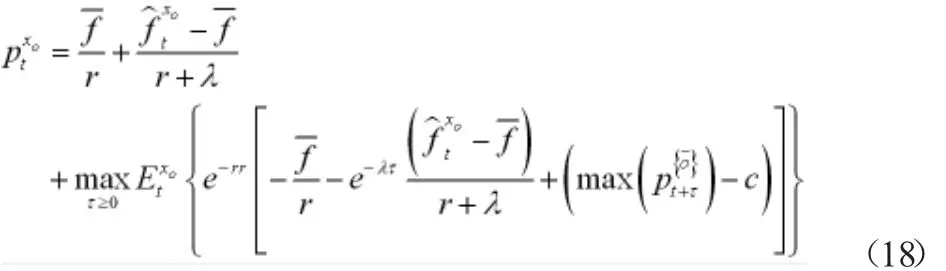
根据Scheinkman和Xiong（2003），假设本文的价格函数的均衡形式如下，

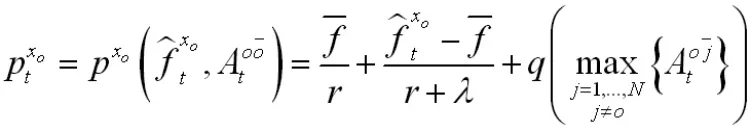
其中q＞0和q'＞0。因此，该函数可以写做

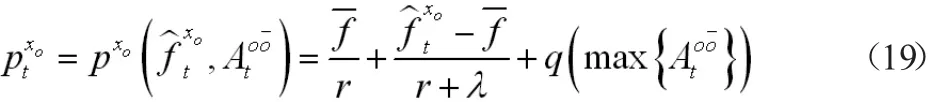
假设在时间t+τ，组xm(xm∈{x0})具有与组x0的信念的最大差异，且最大预留价格pt+τxm由组xm提出。根据（19）式，且{xm}∈可得

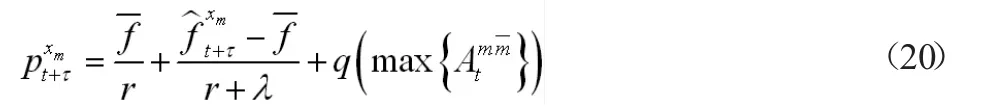
将式（20）代入（18），得到

因此，再售期权的价值可以写为

由于存在（19）式的均衡形式，需要构建满足等式（22）的价值函数q。资产所有者可以选择在最优行权时间以价格行权。

式（14），（17）和（18）表明资产的价格具有有限的形式，但再售期权q的价值取决于下一个期权价值，因此形成最优执行价格的无限形式。

六、总结

本文构建一个N维模型来讨论金融泡沫和单位资产定价。假设可以收集到一组关于所有投资者信号的向量，但他们对其信号的信息水平的高估会引起对资产的未来股利的异质信念。根据由两个噪声和组成的新信号，计算得出条件方差的平稳解，并导出每小组的条件均值的演变。接着得出所有组之间异质信念的N维矩阵。

本文基于这种异质信念来定义交易的定价方案。考虑卖空限制和有限数量资产对应的无限买家条件，本文选择当前所有者想要出售资产时下一个买家的最大保留价格作为资产定价。其中，再售期权也选择了当前所有者和潜在买家之间最大信念差异。

虽然Scheinkman和Xiong（2003）0给出了二维的均衡形式，但N维的均衡形式仍然需要通过其他有效的方法来解决。同时，本文再售期权的递归结构也难以导出期权均衡价值。

[1]JoseAScheinkman and WeiXiong.Overconfidence and speculative bubbles.JournalofpoliticalEconomy,111(6):1183-1220,2003.

[2]Robert JShiller,Stanley Fischer,and Benjamin M Friedman.Stock prices and social dynamics.Brookings papers on economic activity, 1984(2):457-510,1984.

[3J Bradford DeLong,Andrei Shleifer,Lawrence H Summers,and Robert JWaldmann.The survival ofnoise tradersin financial markets, 1988.

[4J Bradford De Long,Andrei Shleifer,Lawrence H Summers,and Robert J Waldmann.Positive feedback investment strategies and destabilizing rational speculation.The Journal of Finance,45(2): 379-395,1990.

[5]Richard Topol.Bubbles and volatility of stock prices:effect of mimeticcontagion.TheEconomicJournal,101(407):786-800,1991.

[6]W David Allen and Dorla A Evans.Bidding and overconfidence in experimentalfinancialmarkets.TheJournalofBehavioralFinance,6(3): 108-120,2005.

[7]Edward M Miller.Risk,uncertainty,and divergence ofopinion.The Journaloffinance,32(4):1151-1168,1977.

[8]JMichaelHarrisonandDavidMKreps.Speculativeinvestorbehavior in a stock market with heterogeneous expectations.The Quarterly JournalofEconomics,pages323-336,1978.

[9]Robert Shevilevich Liptse,Albert Nikolaevich Shiryayev,and AB Aries.StatisticsofrandomprocessesII:Applications.Springer,1978.

[10]TimothyG Conley,LarsPeterHansen,Erzo GJLuttmer,andJoseA Scheinkman.Short-term interest rates as subordinated diffusions. ReviewofFinancialStudies,10(3):525-577,1997.

方灿琦，上海海事大学经济管理学院研究生。

F830

A

1008-4428（2017）04-77-04