12kV真空断路器半双稳态永磁机构的设计

王凯东， 王 毅， 张明志

(北京交通大学电气工程学院， 北京 100044)

12kV真空断路器半双稳态永磁机构的设计

王凯东， 王 毅， 张明志

(北京交通大学电气工程学院， 北京 100044)

应用于真空断路器的永磁操动机构一般分为双稳态和单稳态永磁机构。对于单稳态永磁机构，通过调整分闸弹簧在分闸位的预拉力，可以实现对分闸特性的调节。增大预拉力可以缩短分闸时间，降低分闸弹跳，但预拉力过大会导致合闸状态时的保持合力减小，可能造成合闸的不可靠，也会对合闸动态特性造成不利影响，如合闸时间增加等。本文提出了应用于12kV真空断路器的半双稳态永磁机构的设计方法，该机构在分闸状态由较小的永磁保持力和弹簧力共同实现分闸保持。分闸位保持力大有助于抑制分闸弹跳，同时永磁保持力在动铁芯离开分闸位置后迅速减小，对合闸保持以及合闸动态特性几乎没有不利影响。利用Ansoft Maxwell软件建立永磁机构模型，进行静态和动态的仿真。根据设计结果制作实际样机，对其进行测试，实验结果验证了设计与仿真的正确性。

永磁机构； 半双稳态； 设计； 真空断路器

1 引言

永磁操动机构真空断路器具有免维护、寿命长、可靠性高、可以频繁操作等众多优点，其应用领域愈来愈广泛。20世纪90年代末，ABB Calor Emag公司推出了VMI型永磁式真空断路器，引起了国内外的普遍关注。永磁操动机构根据其工作原理可分为双稳态和单稳态永磁机构，二者在合闸特性方面比较相似，但分闸特性有较大差异。双稳态永磁机构与断路器的分闸负载特性不相匹配，而单稳态永磁机构的分闸速度特性与弹簧操动机构较相似，具有刚分点前加速、刚分点后减速的优点[1]，广泛地应用在中压断路器中。本文提出一种半双稳态永磁机构的设计方法，所谓半双稳态，即分合闸共用一个线圈，采用电磁合闸与弹簧分闸，合闸状态永磁保持，分闸状态由较小的永磁保持力和弹簧力共同实现分闸保持。

2 永磁机构设计前处理

图1为配半双稳态永磁机构的真空断路器结构示意图。左侧为真空灭弧系统，采用某公司的TGD-12/4000-31.5UH3型真空开关管固封极柱，额定工作电流4000A，额定短路开断电流为31.5kA，表1给出了该型号真空灭弧室的主要技术参数。

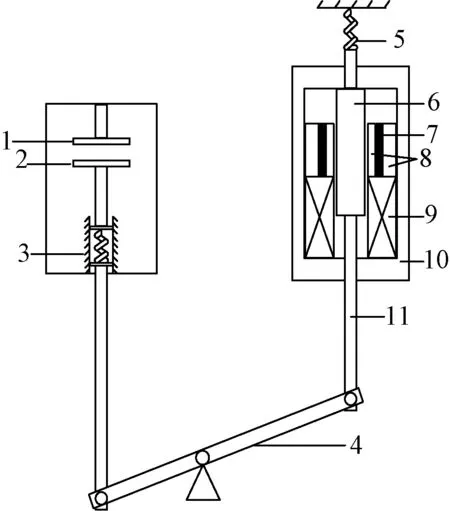
1—静触头; 2—动触头; 3—触头弹簧; 4—连杆; 5—分闸弹簧; 6—动铁心; 7—永磁体; 8—导磁环; 9—线圈; 10—磁轭； 11—驱动杆图1 配半双稳态永磁机构的真空断路器示意图Fig.1 Schematic diagram of vacuum circuit breaker with half bistable state permanent magnetic actuator

表1 真空灭弧室主要技术参数
Tab.1 Main technical parameters of vacuum arc extinguishing chamber

参数数值额定电压Ur/kV12额定电流Ir/A4000额定短路开断电流Isc/kA31.5触头自闭力/N220±50额定触头压力/N3100±200触头初压力/N2200±200触头开距/mm9±1超行程/mm4±1额定开距下的触头反力/N320±50真空开关管运动部分质量/kg2.5

触头初压力、终压力、开距和超行程是开关电器的4个主要触头参数，是对开关电器操动机构设计的依据。根据表1，12kV真空灭弧室触头开距取9mm，超行程取3mm，触头自闭力取220N，触头初压力取2200N，触头终压力取3100N，采用这些参数进行计算。该永磁机构的动铁心行程设计为22mm，故永磁机构传动系统的传动比，即断路器触头侧导杆长度与永磁机构侧的导杆长度之比为6/11。分闸弹簧个数为2，每个弹簧的弹性系数为19N/mm。

首先，将灭弧室侧参数折算到操动机构侧，结果如表2所示。

表2 灭弧室侧参数折算到操动机构侧的值Tab.2 Parameter values of operating mechanism converted from parameters of arc extinguishing chamber

根据上述参数计算永磁体保持力F：

F=(1+k)[ni(F1-F2+m1g)-m2g+F3]

(1)

式中，k为安全系数，根据经验选取范围在0.2～0.3，本文取0.3；n为断路器相数，若为单相则取1，三相取3，本方案取1；i为传动系统的传动比，若为直动式结构则取1，本方案取为6/11；m1为真空开关管运动部分质量， 2.5kg；m2为操动机构运动部分质量，包括动铁心和驱动杆，根据经验近似取5kg；F1为额定触头压力， 3100N；F2为灭弧室自闭力， 220N；F3为分闸弹簧在合闸位置时的拉力，计算为1216N。将以上参数值代入式(1)求得F为3600N，本文取保持力为4000N。

3 半双稳态永磁操动机构结构设计

3.1 动铁心与驱动杆尺寸设计

本文所设计的永磁机构为圆形机构，动铁心采用电工纯铁，利用麦克斯韦电磁吸力公式可计算动铁心截面积，如式(2)所示：

(2)

式中，B1为工作气隙的磁通密度；S为动铁心的表面导磁面积；μ0为真空磁导率，4π×10-7H/m。

工作气隙的磁通密度B1的选择很重要，通常取动铁心所用材料的磁化曲线膝点附近的数值[2]，本文取1.5T。计算求得动铁心表面导磁面积S=4468mm2。驱动杆的直径取为14mm，其材料为不锈钢。动铁心的半径R1可通过式(3)求得：

S1=S+S2

(3)

式中，S为动铁心的表面导磁面积；S1为动铁心总面积，S1=πR12；S2为驱动杆截面积，S2=πR22，其中R2为驱动杆半径。

代入数值求得动铁心的半径R1为39mm，则合闸保持时气隙磁通为：

Φ=B1S=6.94×10-3Wb

(4)

3.2 永磁体尺寸设计

永磁机构的性能、设计制造特点等都与永磁材料的性能密切相关。本文的永磁体选用钕铁硼材料，是目前磁性能最好的永磁材料。其退磁曲线全部为直线，回复线与退磁曲线基本重合[3]，可以使永磁机构的磁性能在运行过程中保持稳定。图2为钕铁硼的退磁曲线。

图2 钕铁硼的退磁曲线Fig.2 Demagnetization curve of NdFeB

永磁体选用某公司生产的N38型烧结钕铁硼。其剩余磁感应强度Br为1.26T，矫顽力Hc为899kA/m，其工作点的确定是设计的关键。

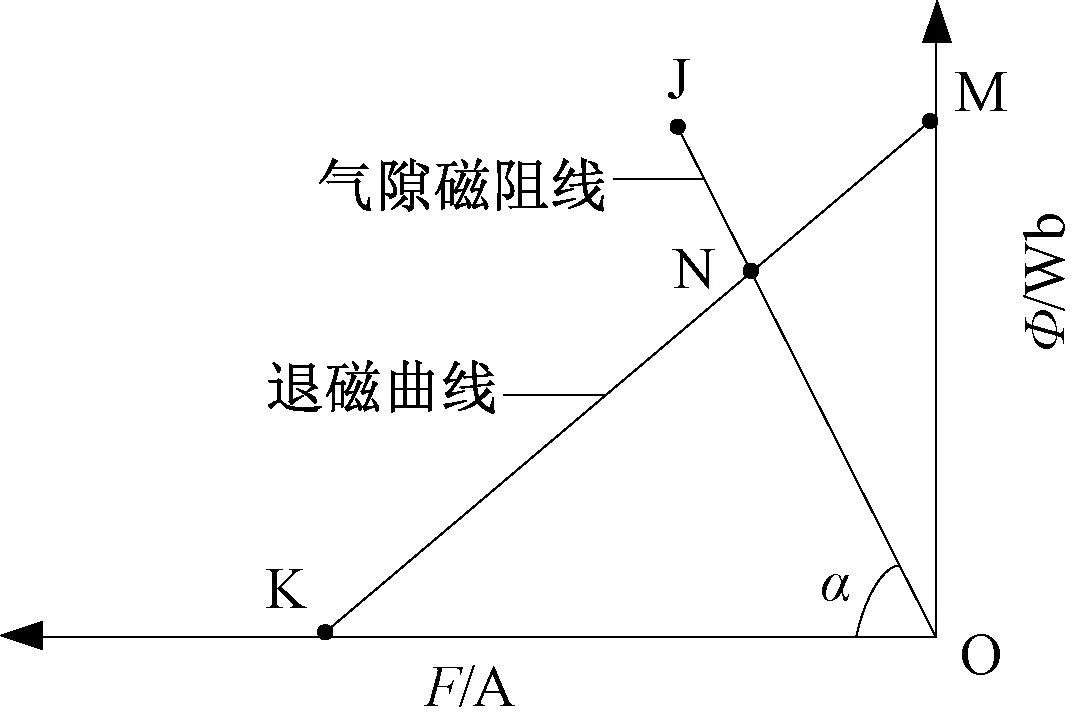
图3 钕铁硼工作点的确定Fig.3 Determination of working point of NdFeB

(1)永磁体高度h的确定

一些文献常用最大磁能积作为设计依据，还有一些文献所用永磁体的工作磁密为剩磁的75%[4]，本文选择永磁体的工作磁密B2为剩磁Br的60%，则永磁体的截面积S3为：

(5)

永磁体采用扇形结构，每块跨圆周45°，共八块。图1中，用两个导磁环把永磁体固定，取内导磁环与动铁心的间隙为1mm，并设内导磁环的厚度为7mm，则永磁体的高度计算公式为：

(6)

式中，D为永磁体的内径，为94mm。求得永磁体的高度h为31mm。

(2)永磁体厚度l的确定

在合闸位置，要保证动铁心与静铁心之间有足够的吸力，永磁体必须能供给足够的磁动势。所以首先需估算磁路消耗的磁动势，其包括以下两方面。

1)气隙消耗的磁动势

气隙消耗的磁动势与磁通密度B和气隙长度δ相关。如图4所示，动铁心与静铁心间的主气隙δ1=0.1mm。4个非主气隙[5]分别为：动铁心与内导磁环之间的气隙δ2=1mm，内导磁环与永磁体之间的气隙δ3，永磁体与外导磁环之间的气隙δ4，磁轭与下端盖板之间的气隙δ5，且δ3=δ4=δ5=0.1mm。主气隙的磁密B1=1.5T，设非主气隙的磁密B2=1.1T，则磁路气隙消耗的磁动势IN1为：

(7)

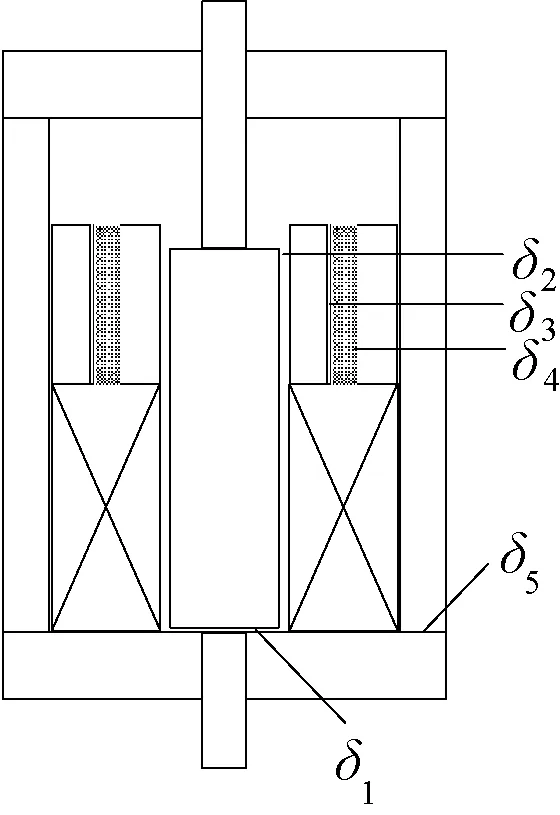
图4 主气隙与非主气隙示意图Fig.4 Schematic diagram of main air gap and non main air gap

2)动铁心和磁轭等磁路部件消耗的磁动势

各磁路部件消耗的磁动势与磁通密度B的大小和材料性质有关。本文选取Q235钢作为导磁材料。设动铁心磁密为B3，其余磁路部件磁密为B4，则各部件消耗的磁动势IN2为：

(8)

式中，μr为Q235钢的相对磁导率；l1为磁路在动铁心中的长度；l2为磁路在其余导磁部件中的长度。

由于磁轭和动铁心的全部尺寸还未知，所以需要假设磁路消耗的总磁动势IN为1800A。则l的计算公式为：

(9)

式中，H为永磁体的工作点处的磁场强度，大小为359.6kA/m，代入求得永磁体的厚度l=5mm。

最后确定永磁体的高度h为31mm，厚度l为5mm，每块跨圆弧45°，共八块。

3.3 线圈的设计

本文设计的是单线圈永磁机构，即合分闸共用一个线圈。分闸时，只需通以与合闸操作时方向相反的电流即可。下面首先分析操动机构的反力特性。

合闸过程中涉及到的反力主要为触头的自闭力、灭弧室侧和操动机构侧运动部件的重力、分闸弹簧拉力、触头弹簧压力等。根据灭弧室侧归算到操动机构侧的参数值，可求得操动机构的反力特性。

在合闸过程中，设动铁心的位移为x(mm)，则x∈[0，22]。触头反力可以看成是一个弹性阻尼，随着触头的闭合逐渐减小[6]，刚合闸时触头反力减为零，折算后可以表示为175-10.6x(N)。分闸弹簧的弹力公式为：380+38x(N)。

合闸过程中动铁心向下运动，整个过程可分为以下两部分。

1)当0≤x≤16.5时，此阶段存在的反力为触头自闭力、触头反力、分闸弹簧拉力、灭弧室侧运动部件折算到操动机构侧的重力、操动机构侧运动部件重力。故此阶段的反力公式可表示为：

(10)

2)当16.5≤x≤22时，此阶段存在的反力为触头自闭力、分闸弹簧拉力、操动机构侧运动部件重力、触头弹簧的反力。此阶段的反力公式可表示为：

(11)

综上，可得到操动机构的反力函数方程：

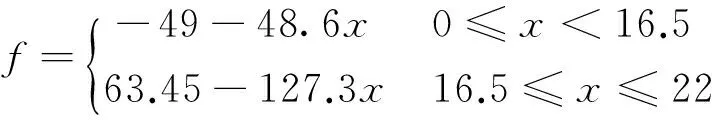
(12)

根据式(12)，可以得出归算后的操动机构反力特性，如图5所示。

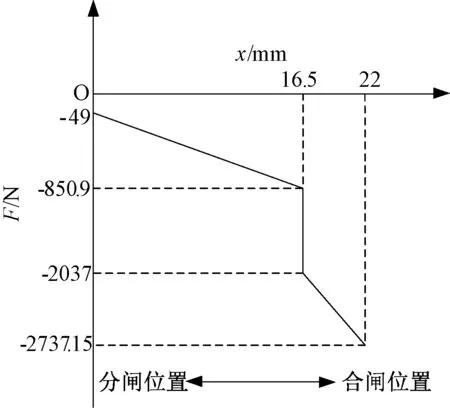
图5 归算后的操动机构反力特性Fig.5 Reaction force characteristic of operating mechanism after conversion

图6为永磁机构吸力与反力特性图。曲线A为合闸过程中动铁心受到的电磁吸力，曲线B为归算后的操动机构反力特性，曲线C为永磁体产生的吸力，曲线D为A与C两方面的力叠加后的总合闸吸力特性。可以看出，从合闸起始位置至触头刚合位置所需要的合闸力较小，一旦触头弹簧开始压缩，所需要的合闸力会突然增大。

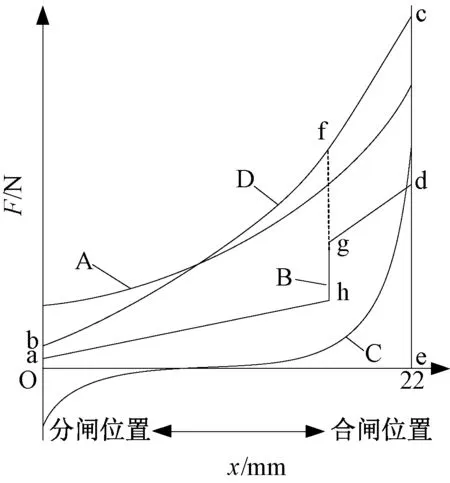
图6 永磁机构吸力与反力特性Fig.6 Suction and counter force characteristics of permanent magnetic actuator

真空断路器与永磁机构两者理想的合闸配合，不仅要求点b高于点a，点f高于点g，而且要求obce的面积大于oahgde的面积[7]。

线圈励磁方式采用电容放电励磁，以合闸过程为例，在分闸位置，线圈提供的电磁吸力要足以克服永磁体在分闸位置的保持力和各种机械反力，才能保证断路器成功合闸。

合闸过程初始需要线圈提供的电磁合闸力F合为：

F合=F永-(F2+F4-m1g)i-m2g+F分

(13)

式中，F永为分闸状态时永磁体的保持力，大小取为1500N；F2为触头自闭力，220N；F4为触头反力，320N；m1为真空开关管运动部分质量，2.5kg；m2为操动机构运动部分质量，5kg；i为传动系统的传动比， 6/11；F分为分闸弹簧预拉力， 380N。经计算，得出F合=1450N。

线圈向气隙提供的磁动势包括：主气隙中的磁压降、非主气隙的磁压降和各导磁部件的磁压降，即

IN=INδ+∑(IN)δ′+∑(IN)1

(14)

式中，INδ为主气隙中的磁压降；∑(IN)δ′为非主气隙的磁压降总和；∑(IN)1为各导磁部件的磁压降总和。

根据麦克斯韦电磁吸力公式F合=Bδ2S/(2μ0)，可求出线圈向气隙提供的磁密Bδ为0.9T，再由公式：

(15)

求得主气隙中的磁压降INδ为15756A。

初步设计时，一般取非工作气隙的磁压降与导磁体各部分磁压降为气隙磁压降的0.2～0.55倍[8]。本文取0.4，则线圈向气隙提供的磁动势为：

IN=1.4INδ=22058(A)

(16)

设合闸线圈通过的工作电流峰值Im为30A，则线圈匝数为：

(17)

这里取整数，选为700匝。

动铁心与线圈间隙取1mm，线圈的内径为80mm，并设其厚度为20mm，则线圈的外径为120mm，线圈的平均直径D1为100mm。利用式(18)可以求得线圈导线直径：

(18)

整理后得到线圈铜导线直径d的公式为：

(19)

式中，d为线圈铜导线的直径；lpj为线圈平均匝长，lpj=πD1；ρ为铜的电阻率， 0.02029Ω·mm2/m；U为线圈的电压， 220V；IN为线圈提供的磁动势。

代入数据得d=0.902mm，按照漆包线国家标准GB6109.1-90的规定，取铜导体的直径为0.9mm，将其按照二级漆膜处理后，得到漆包线的外径为0.989mm。

由于线圈厚度为20mm，取横向绕16层，纵向匝数为44匝，线圈高度为55mm。

3.4 上下端盖和磁轭的设计

磁轭的内半径Rcn可以根据3.3节所求的线圈外半径来决定，为60mm，取其厚度为15mm，则外半径Rcw为75mm，磁轭导磁面积为：

(20)

Sc大于动铁心的导磁面积S，符合要求。上下端盖的半径为75mm，因分闸永磁保持力比合闸保持力小得多，故上端盖材料应选为导磁材料，且动铁心在分闸位置时与上端盖的接触面积应小于合闸时与下端盖的接触面积。由于接触面积小，设计时需将此接触部分做成凸起的空心圆台，上端盖其余部分与动铁心留有约5mm的气隙。动铁心受到反向的永磁保持力，而此反向保持力可有效减小断路器的分闸反弹，以避免分闸后重燃引起事故。两端盖由于会受到动铁心的撞击，二者的厚度暂取15mm。下端盖还需固定线圈，所以需要设计台阶定位，具体尺寸可根据仿真结果再继续调整。上下端盖和磁轭的材料统一使用Q235钢。

4 永磁机构的动静态仿真

按照第3节设计的结构参数，用Ansoft Maxwell软件建立永磁机构的模型[9,10]，然后对其进行动静态的仿真。

4.1 永磁机构静态吸力特性

永磁机构的二维和三维模型如图7所示。永磁机构的静态吸力特性如图8所示。

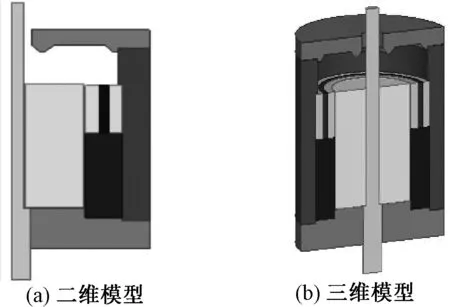
图7 永磁机构模型Fig.7 Model of permanent magnetic actuator

图8 动铁心在行程不同位置时所受到的永磁吸力Fig.8 Permanent magnetic suction force of moving iron core in different position

永磁体单独作用且机构线圈中无电流通过时，动铁心处于行程不同位置时磁场的分布情况如图9所示。

图9 永磁体单独作用时机构的静态磁场分布Fig.9 Static magnetic field distribution with single action of permanent magnet

4.2 机构驱动电路模型

动态特性仿真时，通过Maxwell Circuit Editor编辑外电路，如图10所示。其中C为电容，R和L分别为线圈的等效电阻和等效电感。永磁机构在工作时，电容被预先储能，通过回路对线圈进行放电，线圈获得电流后产生的磁动势推动铁心运动。电容初始电压为250V，电容大小为10000μF。

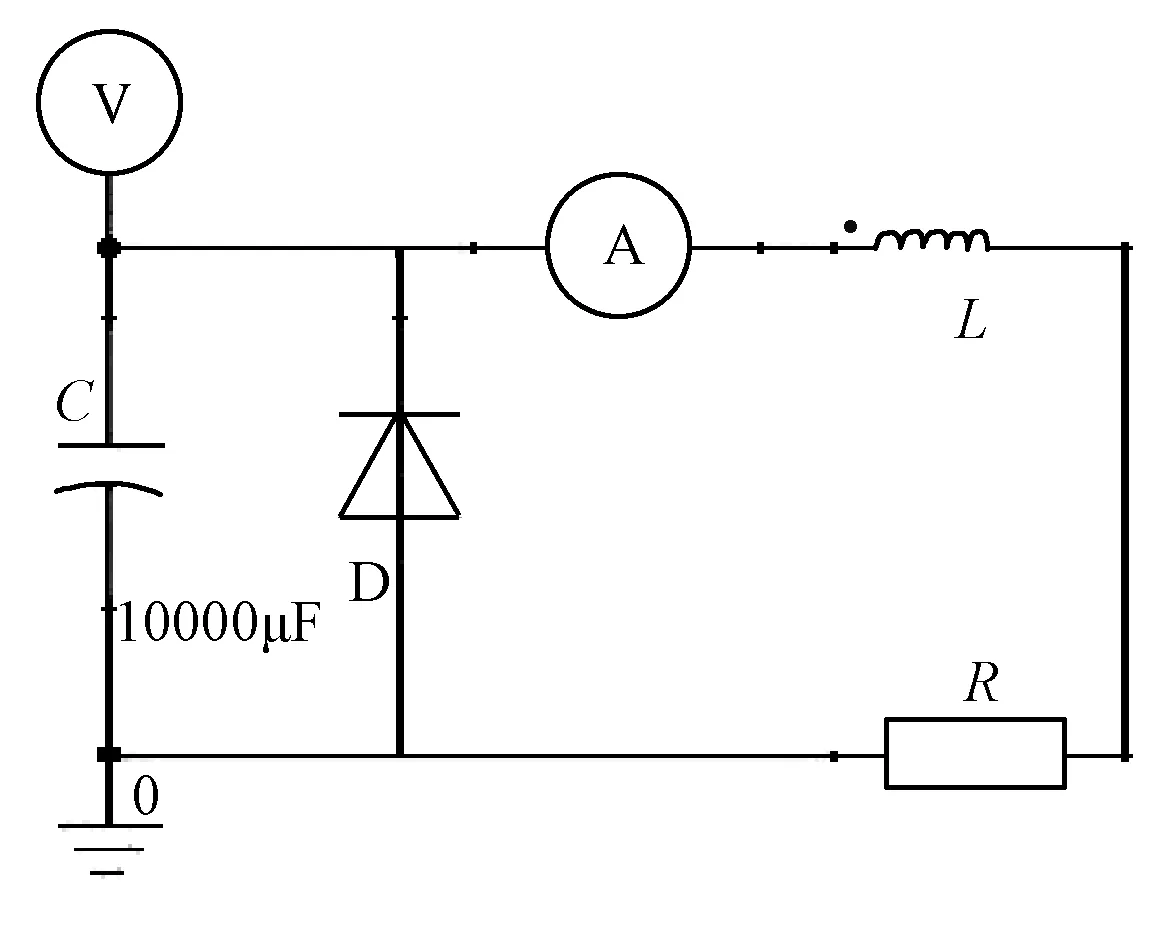
图10 电容供电的励磁电路Fig.10 Excitation circuit with capacitive power supply

4.3 动态特性

对永磁机构的合闸与分闸过程分别进行仿真，得到动铁心从分闸位置运动到合闸位置所需时间为29.5ms，从合闸位置运动到分闸位置所需时间为20ms。合闸过程中线圈峰值电流为18.6A，分闸过程中线圈的峰值电流为5.37A。

5 实验结果及分析

5.1 永磁机构静态保持力测试

永磁机构静态吸力测试的装置如图11所示。根据设计，在机构中放置8块永磁体，测得的合闸保持力为4800N，分闸保持力为1900N，数值都偏大。调整永磁体的数量为7块，测得的合闸保持力为4100N，分闸保持力为1600N。

图11 永磁机构静态保持力测试装置图Fig.11 Testing device diagram for static retaining force of permanent magnetic actuator

5.2 永磁机构动态特性测试

对样机进行合闸和分闸的测试，图12为实验与仿真的合闸动态曲线对比图，图13为实验与仿真的分闸动态曲线对比图。

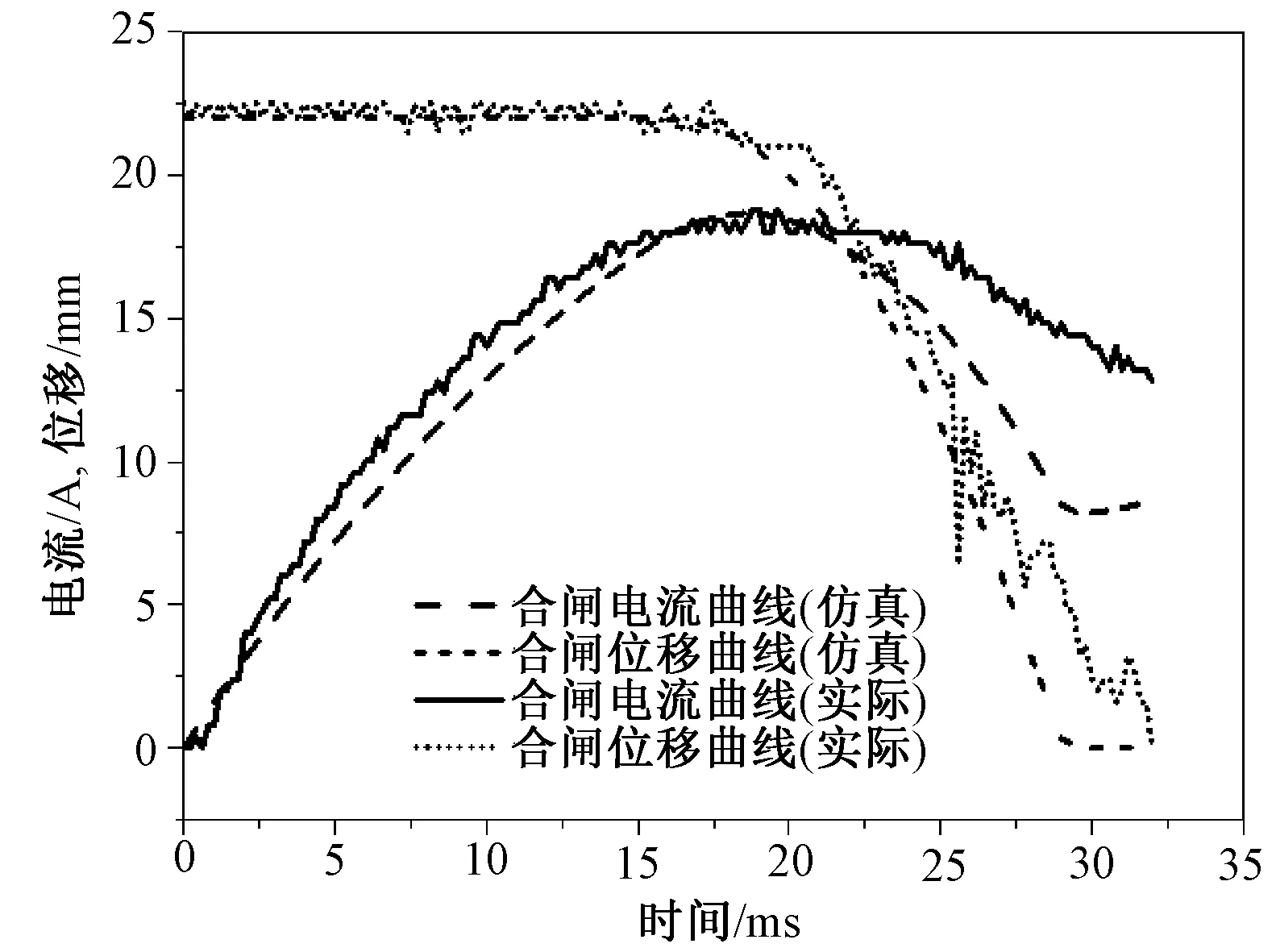
图12 合闸过程的电流与位移曲线Fig.12 Actual current and displacement curve of closing process

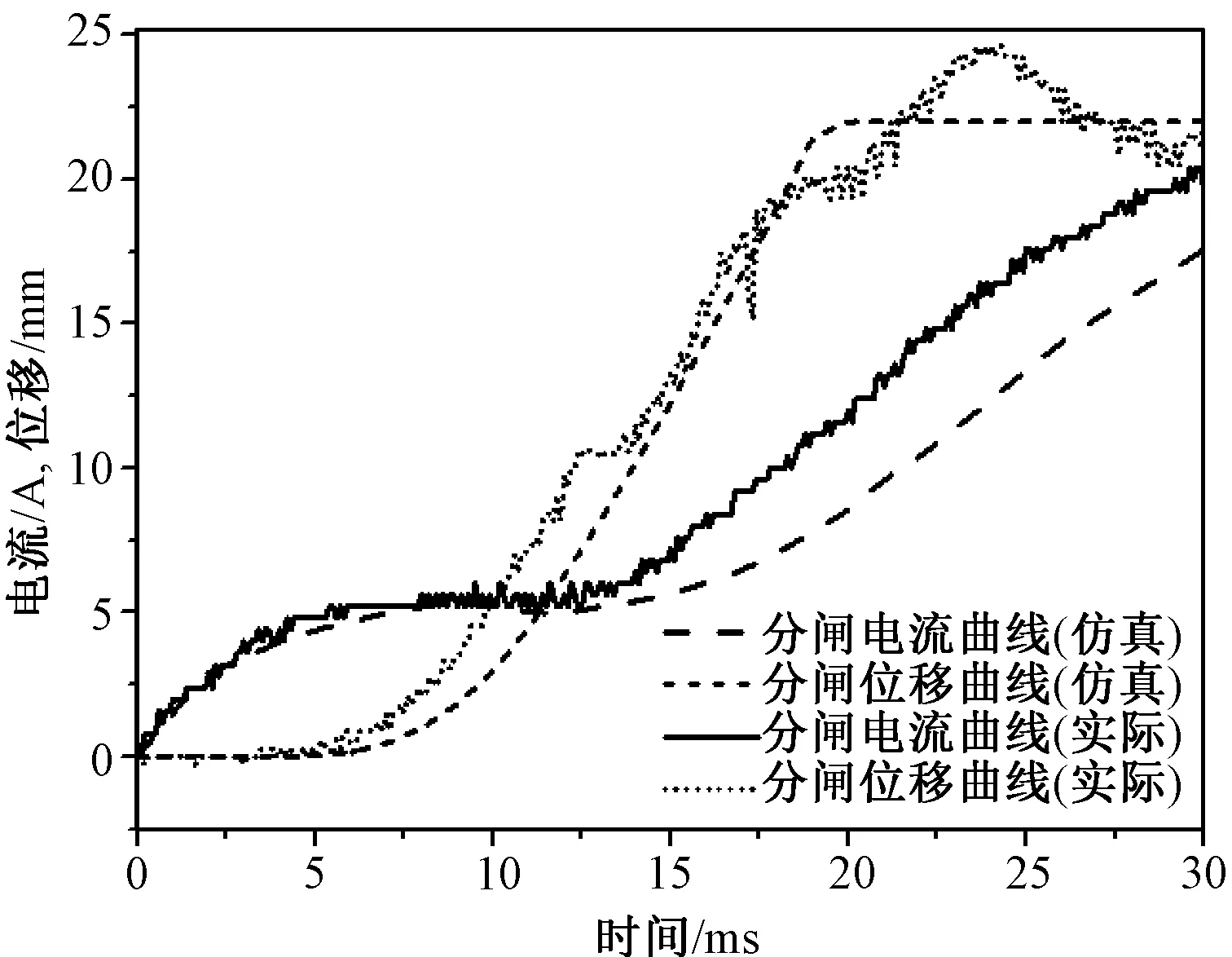
图13 分闸过程的电流与位移曲线Fig.13 Actual current and displacement curve of opening process

在实际合闸测试中，合闸电流峰值为19A，合闸时间为32ms；分闸电流峰值为5.2A，分闸时间为22ms。表3为仿真与实测结果的误差表。

表3 仿真与实测的误差表Tab.3 Error table of simulation and actual measurement

由于实际的分合闸保持力比仿真结果偏大一些，这会导致实际的分合闸时间比仿真所得时间略长一些，再加上环境及实验方法的影响，现场测试不可避免地会产生误差，但从表3中可以得出，实测结果与仿真结果比较接近，误差在允许范围内。

6 结论

本文介绍了一种半双稳态永磁机构的设计方法，并通过Ansoft Maxwell软件建立机构模型，进行仿真，得到永磁机构的静态和动态特性。根据仿真结果确定的最后机构参数，制作样机进行实际测试，实测值与仿真结果吻合，说明了该设计方法的准确性和仿真的可靠性。该机构分闸状态由较小的永磁保持力和弹簧力共同实现分闸保持，其需要的合闸保持力比仅由弹簧力提供相同分闸保持力的单稳态机构小。在合闸过程中，分闸端的弹簧预拉力很小，且永磁吸力迅速减小，相比于一直存在较大弹簧预拉力的单稳态机构，其合闸速度要快。在半双稳态永磁机构中，动铁心在分闸保持时受到反向永磁吸力，该反向保持力可有效减小断路器的分闸反弹，从而避免分闸后重燃引起事故。本文为设计不同电压等级或不同结构的永磁机构提供了较好的依据和参考。

[1] 林莘(Lin Xin). 永磁机构与真空断路器 (Permanent magnetic actuator and vacuum circuit breaker) [M]. 北京：机械工业出版社 (Beijing: China Machine Press), 2002.

[2] 谭东现(Tan Dongxian). 永磁操动机构设计与动态分析软件的开发(The design of permanent magnetic actuator and development of dynamic analysis software) [D]. 沈阳：沈阳工业大学 (Shenyang：Shenyang University of Technology)，2006.

[3] 游一民, 张敬菽, 陈德桂(You Yimin，Zhang Jingshu，Chen Degui). 关于永磁机构一些问题的讨论 (Discussion on some problems of permanent magnetic actuator) [A]. 全国智能化电器及应用研讨会(National Symposium on Intelligent Electrical Apparatus and Applications) [C]. 2001. 110-115.

[4] 左全璋，胡双，左才科(Zuo Quanzhang，Hu Shuang，Zuo Caike). 双稳态永磁操动机构结构设计和性能计算(Structural design and performance calculation for flip-flop permanent magnetic operating mechanism) [J]. 华通技术(Huatong Technology)，2002，(2)：13-17.

[5] 游一民，陈德桂，孙志强，等(You Yimin, Chen Degui, Sun Zhiqiang, et al.). 基于动态分析的永磁机构最佳设计参数的选择(Optimal design of permanent magnetic actuator based on dynamic behavior analysis)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering & Energy)，2004，23(1)：43-46.

[6] 石运强(Shi Yunqiang). 永磁式真空断路器操作机构的研究(Study on the operating mechanism of permanent magnetic vacuum circuit breaker) [D]. 成都：西南交通大学(Chengdu：Southwest Jiaotong University)，2012.

[7] 魏本纪(Wei Benji). 双稳态永磁操动机构与真空断路器的特性配合问题探讨(Discussion on the coordination of the characteristics of the double steady state permanent magnetic actuator and vacuum circuit breaker) [J]. 高压电器(High Voltage Apparatus)，2002，38 (1)：27-30.

[8] 夏克鹏(Xia Kepeng). 开关电器中永磁操动机构设计与仿真分析(Design and simulation analysis of permanent magnetic actuator in switching device) [D]. 沈阳：沈阳工业大学(Shenyang：Shenyang University of Technology)，2010.

[9] 刘志远，谢克松，王仲奕，等(Liu Zhiyuan, Xie Kesong, Wang Zhongyi, et al.). 杯状纵磁真空灭弧室三维涡流场仿真(Analysis of 3D eddy current field in cup-type axial magnetic field vacuum interrupter) [J]. 电工电能新技术(Advanced Technology of Electrical Engineering & Energy), 2004，23(2)：26-28.

[10] 郭凤仪，李朋，李斌，等(Guo Fengyi，Li Peng，Li Bin，et al.). 电磁操动机构的电磁缓冲仿真实验研究(Simulation and experimental research on electromagnetic buffer of electromagnetic actuator) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering & Energy), 2010，29(3)：68-71.

Design of half bistable permanent magnetic actuator used in 12kV vacuum circuit breaker

WANG Kai-dong, WANG Yi, ZHANG Ming-zhi

(School of Electrical Engineering, Beijing Jiaotong University, Beijing 100044, China)

The permanent magnetic actuator used in vacuum circuit breaker is generally divided into bistable state and single steady state permanent magnetic actuator. For the single steady state permanent magnetic actuator, it can achieve the regulation of break-brake characteristics by adjusting the pretension of the break-brake spring in the open position. Increasing the pretension can shorten the opening time and reduce the switch-off bounce. But if the pretension is too large, it will lead to the decrease of the resultant force in the closing state, and this may cause the unreliability of closing operation. The pretension will be also unfavourable to the dynamic characteristics of the closing process, such as the increase of the closing time,etc. This paper presents the design method of a half bistable permanent magnetic actuator used in 12kV vacuum circuit breaker, and the actuator maintains in the opening position by a small permanent magnetic retaining force and a spring force. Large retaining force in the open position helps to restrain the switch-off bounce. At the same time, the permanent magnetic retaining force decreases rapidly after the moving iron core leaves the open position, and it almost has no adverse effects on the closing retaining force and the dynamic characteristics of the closing process. Ansoft Maxwell software is used to establish the model of permanent magnetic actuator to carry out the static and dynamic simulation. An actual prototype has been made according to the results of the design, and it has been tested. The results have verified the correctness of the design and the simulation.

permanent magnetic actuator; half bistable state; design; vacuum circuit breaker

2016-05-20

王凯东(1991-)， 男， 河北籍， 硕士研究生， 研究方向为智能电器； 王 毅(1958-)， 男， 辽宁籍， 教授， 博士， 研究方向为智能电器、 电力设备在线监测、 气体放电在环保中的应用等。

TM561

A

1003-3076(2017)04-0029-08