PCC点系统侧戴维南等值电路参数的估计方法研究
张 坤, 戴传凯, 孙媛媛, 尹志明
(1. 山东大学电气工程学院, 山东 济南 250061;2. 国网潍坊供电公司, 山东 潍坊 261021;3. 国网北京市电力公司培训中心, 北京 100041)
PCC点系统侧戴维南等值电路参数的估计方法研究
张 坤1, 戴传凯2, 孙媛媛1, 尹志明3
(1. 山东大学电气工程学院, 山东 济南 250061;2. 国网潍坊供电公司, 山东 潍坊 261021;3. 国网北京市电力公司培训中心, 北京 100041)
电力系统中PCC点系统侧戴维南等值电路参数的准确估计对电网的安全稳定分析具有重要意义。本文首先根据系统的戴维南等值电路模型,分析了等值电路参数估计的难点在于克服系统侧和负荷侧参数同时波动的影响。进而提出利用偏最小二乘回归法列写回归方程估计系统侧的等值电源和阻抗参数。为提高准确性,文中基于变电站的电压、电流实测数据,结合电压和负荷的波动概率,提出了数据选择的指标,筛选出系统侧保持恒定而负荷侧有较大波动的数据。同时基于实测数据的分析对数据选择指标的取值规律进行了研究。本文方法可有效估计出正序、负序以及谐波频率下系统侧的戴维南等值电路参数,实际算例分析验证了所提方法的有效性。
戴维南等值参数; 偏最小二乘法; 数据筛选; 基波分量; 谐波
1 引言
电力系统中公共耦合点(Point of Common Coupling, PCC)处的系统侧戴维南等值电路参数在电压稳定性分析、无功功率补偿器和无源滤波器的设计等诸多方面均有着重要的应用[1-4]。对电力系统PCC点上游侧的系统戴维南等值电路参数进行准确的估计具有重要的理论意义和应用价值。
目前,关于系统侧戴维南等值参数的研究主要分为两类[5]:干预法和非干预法。干预法向系统注入干扰电流或投切负荷,通过节点的电压电流变化来估计系统侧的等值参数[6]。非干预法利用稳态时系统侧和负荷侧所存在的自然扰动估计系统侧的等值参数[7]。为获取准确的系统参数估计值,干预法需要较强的干扰源,因而会对系统的电能质量造成不良影响。非干预法不需要外加激励源,仅依靠系统中存在的自然波动[8,9],操作简单、易于实现,其关键在于如何选择出合适的数据。目前关于非干预法的研究进展如下:基于PCC点电压、电流的波动量对系统侧的稳态阻抗参数进行估计,原理简单、应用广泛[10,11];基于回归分析的方法对系统侧的等值参数进行辨识,具有较高的准确性[12,13];利用小波分析对扰动信号进行处理或根据电力电子装置的开关变化引入电量的波动计算系统的等值阻抗[14,15],这些研究都是该领域非常有益的进展。实际上,将参数估计方法应用于现场数据时,选择出符合参数估计要求的数据并克服异常数据的干扰,是影响算法结果准确性的关键。
本文基于偏最小二乘回归法,对系统侧的戴维南等值参数估计进行了研究。分析了戴维南等值电路参数估计的关键是克服稳态时系统侧和用户侧参数同时波动的影响,针对系统中多个自变量存在相关性时利用PCC点数据对参数估计时会造成误差的问题,采用偏最小二乘回归法列写回归方程,通过求解回归系数估计出系统戴维南等值参数,从而对PCC点的信息进行有效辨识,减小干扰数据对参数估计的不良影响。为提高准确性与可靠性,基于实测数据,提出了数据选择指标,筛选出系统侧基本不变而用户侧有较大波动的最优数据,抑制了系统中存在的噪声。将所提方法用于多个变电站的采样数据,对该时间段内系统侧在基波(正序和负序)、谐波频率下的戴维南等值参数进行了估计,并总结出了数据选择指标取值的一般性规律。
2 戴维南等值参数估计基础
当系统处于稳态时,其戴维南等值电路的参数基本恒定。PCC点的电压、电流所存在的微小变化是由系统侧和负荷侧的波动共同造成。对系统侧等值阻抗参数的估计一般利用PCC点的波动量进行,分析电路如图1所示,其中ES和ZS分别表示系统侧的等值电源和阻抗,ZL表示用户侧的等值阻抗,PCC点的电压U和电流I可通过测量得到。假设系统侧电源的波动量为ΔES,负荷波动等效为负荷阻抗的波动量ΔZL。在t1~t2时间内,PCC点电压和电流的波动量分别为ΔU和ΔI。

图1 系统侧戴维南等值电路Fig.1 Thevenin equivalent circuit
结合图1,根据系统侧和用户侧波动前后PCC点电压和电流的变化可得:
(1)
(2)
对式(1)、式(2)进行整理可得:
(3)
(4)
PCC点的电压和电流波动量之比为:
(5)
由式(5)可知,若该时间段内当ΔES趋近于0,有
(6)
此时由PCC点电压和电流的波动量计算得到的是系统阻抗的负值。相反,若该时间段内ΔZL趋近于0,有
(7)
此时计算得到的是负荷阻抗。因为实际电力系统中,系统和负荷的运行状态存在不确定性[16],使得系统阻抗的估计难度增加,所以克服系统PCC点不良数据的干扰是有效估计出系统侧等值参数的重要前提。
3 系统戴维南等值参数的估计算法
系统PCC点所测得的数据均为相量,包含电压、电流的幅值与相角信息。因此,对于非纯阻性的系统与负荷阻抗可通过复数方程进行分析。用于分析的戴维南等值电路如图2所示,其中ES、RS和XS分别为系统侧的等值电压、电阻和电抗,等值电压的相角为δ。

图2 戴维南等值分析电路Fig.2 Thevenin equivalent analysis circuit
为便于分析,以PCC点的电流I∠0°为参考相量,电压为U∠φ,基于图2电路可得如下方程:
ES∠δ=(RS+jXS)I∠0+U∠φ
(8)
式(8)为复数方程,将其实部与虚部分开整理可得:
(9)
式中,Ux和Uy分别为PCC点电压的实部和虚部;ESx和ESy分别为系统电压的实部与虚部。式(9)中已知变量为I、Ux、Uy,待求的未知变量为ESx、ESy、RS、XS。在实际计算中,要解得系统参数至少需要三组PCC点的电压、电流测量数据,并且这三组数据需要满足系统侧不变、负荷侧波动的条件。基于三组数据可建立六个方程。因不需要同步采样数据,因此这六个方程中包含八个未知数(三组ESx、ESy和一组RS、XS),同时,利用系统侧参数不变条件还可得到两个关于系统电压幅值相等的方程。因此基于测量得到的三组数据将建立含8个未知数的8个方程,对该方程组联立求解,即可得到系统的等值参数。
通过以上分析可知,求解方程式(9)计算系统侧的等值参数需要对测得的数据进行筛选,以消除不良数据的影响,同时得到符合条件的数据,回归分析是解决该问题的有效方法。回归分析模型中,二元回归法对数据统计特性的一致性要求较高;稳健回归法通过加权处理去除掉奇异值,但是缺少对变量相关性的分析。偏最小二乘回归[17-19]是一种有效的多元统计数据分析方法,该方法常用于研究因变量对多自变量的回归建模。相对于传统的多元线性回归模型,它能够在自变量存在严重多重相关性的条件下进行回归建模,更易于辨识系统信息与噪声,并具有每一个自变量回归系数更容易解释的特点。本文采用该方法对系统等值参数进行估计。
分别在自变量集合X(X=[x1,x2,…,xp]n×p,p为自变量个数,n为样本数)和因变量Y(Y=[y1,y2,…,yq]n×q,q为因变量个数) 集合中提取成分t和u(t为x1,x2,…,xn的线性组合,u为y1,y2,…,yq的线性组合)。在提取这两个成分时,为了回归分析的需要,有下列要求:①t和u应尽可能多地携带其各自数据表中的变异信息;②t和u的相关程度能够达到最大。然后分别实施X对t的回归以及Y对t的回归。
如果回归方程已达到满意的精度,则算法终止;否则将利用X被t解释后的残余信息以及Y被t解释后的残余信息进行第2轮的成分提取。如此往复,直到能达到一个较满意的精度为止。具体过程如下:
记自变量的标准化矩阵为E0,因变量的标准化矩阵为F0。根据回归分析的要求可得:
(10)
式中,θ为目标函数,要求取得最大值;ω和c分别为对应两矩阵最大特征值的单位特征向量。
首先,从F0中提取成分u1,u1=F0c1,‖c1‖=1;从E0中提取成分t1,t1=E0ω1,‖ω1‖=1。由于F0只是一个变量,所以c1是一个常数,u1=F0;根据式(10),有
(11)
分别实施E0和F0对t1的回归:
(12)

(13)
(14)
利用偏最小二乘法可有效估计出系统的戴维南等值参数,但是实际系统中存在各种噪声的干扰,所以必须辅以合理的数据选择指标,对实测数据进行筛选,提高系统等值参数估计的准确性和可靠性。
4 数据选择分析
本节根据变电站的实测数据,分析电压和电流的波动特性,并提出数据选择指标。用于分析的实测数据采集于加拿大某市14.4 kV变电站。使用NI DAQ pad-9174数据采集板对变电站二次侧的电压和电流数据进行连续采样,每1秒钟采集6个周波,每个周波256个点。对实测数据进行傅里叶分析得到其正、负序分量以及各次谐波分量。基于对多个变电站的采样数据样本分析,根据数据的概率分布特性,从以下两方面提出数据的选择指标。
4.1 电压波动
由第2节分析可知,基于未经筛选的PCC点实测数据进行参数估计,得到的结果将包含过多的异常值,缺乏足够的参考价值。实际中系统侧的波动是客观存在的,需要将系统侧电压的波动限制在合理的范围内,使之最大化地满足理论推导条件。

(15)
(16)
式中,m为实测数据的样本容量;k1为波动系数。样本标准差反映了某时间段内数据的波动程度,k1的取值与系统侧波动量有关,由如下方法确定。
定义系统电压的波动率FLE为:
(17)
PCC点的电压波动特性与系统侧等值电源的波动特性基本保持一致,因此对实测的PCC点电压数据进行分析,可得其波动率概率曲线,如图3所示。可见,系统侧电压保持较小波动率的概率较高。波动率的概率密度曲线反映了波动率的分布情况,且不同的PCC点电压的波动概率曲线不同。根据数据自身的波动率概率曲线确定波动范围可提高筛选指标的适用性与有效性。在实际电力系统中,由于系统运行方式[21]和上游侧负荷波动等干扰因素,系统侧参数不可能维持恒定不变,而参数估计结果表明,当电压波动率小于0.4%时,可基本认为系统侧不变。k1的值为此概率曲线下该波动率范围对应的概率。

图3 电压波动率概率曲线Fig.3 Voltage fluctuation rate probability curve
所分析的实测电压数据各波动率区间的数据概率密度如表1所示,其中数据概率密度为该区间的数据量与数据总量的比。电压波动率在区间0~0.4%的数据量占总数据量的约43.10%,在区间0~0.8%的数据量占总数据量的约67.78%,说明系统侧参数保持基本恒定的时间较长。为保证数据筛选的准确性,k1的取值需满足系统侧保持不变的要求,通过分析与验证,k1的取值为0.40~0.44时有较好的筛选效果。
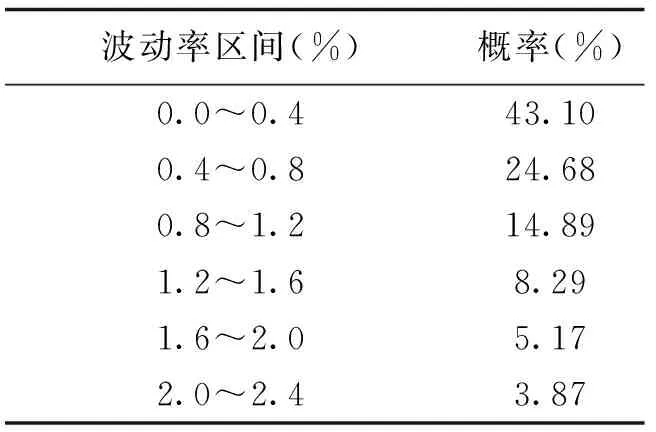
表1 电压波动率概率表Tab.1 Probability of voltage fluctuation rate
4.2 负荷阻抗波动
电力系统中,负荷的波动是随机且呈非线性变化的。负荷的波动导致戴维南等值电路模型中等效的负荷阻抗发生变化。从选择合适数据进行系统侧参数估计的角度,负荷阻抗的波动不宜过小。从求解方程组的角度分析(如文中第3节所述),假设系统侧保持不变,当负荷阻抗波动很小时,PCC点的电压电流波动量也很小,此时方程组中的各方程接近非独立方程,无法求解出系统参数的准确解。因此负荷阻抗的波动范围也应加以合理的限定。根据指标FLE选择出系统侧基本不变的数据后,再从中选择出负荷侧有明显波动的数据。等效的负荷阻抗可由PCC点的实测电压、电流数据计算得出,即
(18)

(19)
(20)
式中,m为样本容量;k2为波动系数;n为每次迭代所用数据点个数。类似地,定义负荷电阻的波动率FLR为:
(21)

图4 负荷的等值阻抗变化图Fig.4 Load equivalent impedance pattern
由实测数据画出的负荷电阻和负荷电抗的波动率概率曲线如图5所示。负荷阻抗波动率的概率曲线总体上不是单调变化的,且负荷电抗的波动率小于负荷电阻。表2给出了负荷阻抗波动率的概率密度分布,可知负荷电阻波动率在区间0.6%~2.4%内的概率密度较大。

图5 负荷阻抗波动率概率曲线Fig.5 Load impedance fluctuation rate probability curve
表2 负荷阻抗波动率概率表
Tab.2 Probability of load impedance fluctuation rate

负荷电阻波动率区间(%)概率(%)负荷电抗波动率区间(%)概率(%)0.0~0.620.840.0~0.234.660.6~1.225.910.2~0.428.821.2~1.826.710.4~0.619.581.8~2.418.150.6~0.89.872.4~3.06.800.8~1.04.703.0~3.61.591.0~1.22.37
为有效剔除异常数据,同时保证负荷侧有一定的波动,负荷阻抗波动率范围选取图5中负荷电阻波动率概率较大的部分1.2%~2.0%。k2的取值方法与k1类似,为所选波动率区间对应的概率。首先,根据负荷阻抗波动率概率曲线确定阻抗波动率区间。当负荷波动较小时,据文中第2节方法进行估计,计算所得的结果是不准确的,当负荷波动较大时,此时的波动不是系统的自然扰动,而是倒闸操作等所引起[22],此部分数据也不能用于估计系统的参数。因此根据阻抗波动率的分布,选取其中概率较大,波动适中的数据。其次,确定所选负荷阻抗波动率区间的概率值, 由此概率值确定k2的值。
通过分析与验证,k2的取值区间为0.35~0.37时可满足数据选择要求。负荷阻抗XL波动范围的选择与RL方法相同。经过k1、k2两指标筛选后的PCC点数据可满足式(12)的计算条件。
5 实测数据验证
基于某市多个14.4 kV变电站的实测数据,利用本文所提方法对变电站母线系统侧的戴维南等值电路参数进行估计,验证所提方法的可靠性。首先对变电站母线的电压和电流进行测量,对所测数据进行傅里叶分析和对称分量变换,求得电压和电流的各序分量和各次谐波分量;再基于第4节所述数据选择方法筛选出系统侧基本保持不变而负荷侧又合理波动的数据;进而根据偏最小二乘法回归方程,对系统侧的等值参数ES、RS、XS进行估计。对每1s内的估计结果取平均值作为该时刻的系统等值参数,最终得到该系统在某一时间段内的系统参数值。
5.1 基波正序系统参数估计
变电站母线的基波正序电压和电流幅值变化如图6所示。基波正序的系统参数估计结果如图7所示。系统参数随时间变化存在着微小波动,这是因为实际系统中的等值电源不可能保持绝对恒定,这与电力系统的实际动态波动是相符的。对计算结果取平均值可作为该时间段内系统参数的估计值。对其他另外三个变电站母线的实测数据也采用同样的方法进行数据选择并估计出系统侧的等值参数,结果如表3所示。

图6 变电站1的PCC点基波正序电压和电流幅值变化图Fig.6 Fundamental frequency positive sequence voltage and current magnitude pattern at PCC of substation 1

图7 基波正序系统参数估计值Fig.7 Fundamental positive sequence system parameters estimation
表3 基波正序系统参数估计均值(50s)
Tab.3 Estimation of fundamental positive sequence system parameters mean value (50s)

ES/kVδ/(°)RS/ΩXS/Ω变电站115.4973.440.712.15变电站215.4072.380.782.03变电站315.4273.560.911.95变电站415.4774.220.852.21
5.2 基波负序系统参数估计
本文所提方法也适合于系统负序和谐波阻抗的估计。三相基波负序分量的大小主要取决于系统的三相不平衡度。变电站1的PCC点负序电压电流幅值如图8所示。用本文方法筛选后的数据估计结果基本保持稳定,没有误差较大的异常值,如图9所示。各变电站的系统等值参数估计值如表4所示。

图8 变电站1的PCC点基波负序电压电流幅值变化图Fig.8 Fundamental negative sequence voltage and current magnitude pattern at PCC of substation 1

图9 基波负序系统参数估计值Fig.9 Fundamental negative sequence system parameters estimation
5.3 5次谐波系统参数估计
以5次谐波为例,应用本文所提方法对系统侧在谐波频率下的等值参数进行估计。对PCC点的数据进行FFT分析,得出5次谐波的电压电流,如图10所示。变电站1所在的5次谐波等值参数估计结果如图11所示。不同变电站的5次谐波系统等值参数估计值如表5所示。

表4 基波负序系统参数估计均值(50s)Tab.4 Estimation of fundamental negative sequence system parameters mean value (50s)

图10 变电站1的PCC点5次谐波电压电流幅值变化图Fig.10 5th harmonic voltage and current magnitude pattern at PCC of substation 1
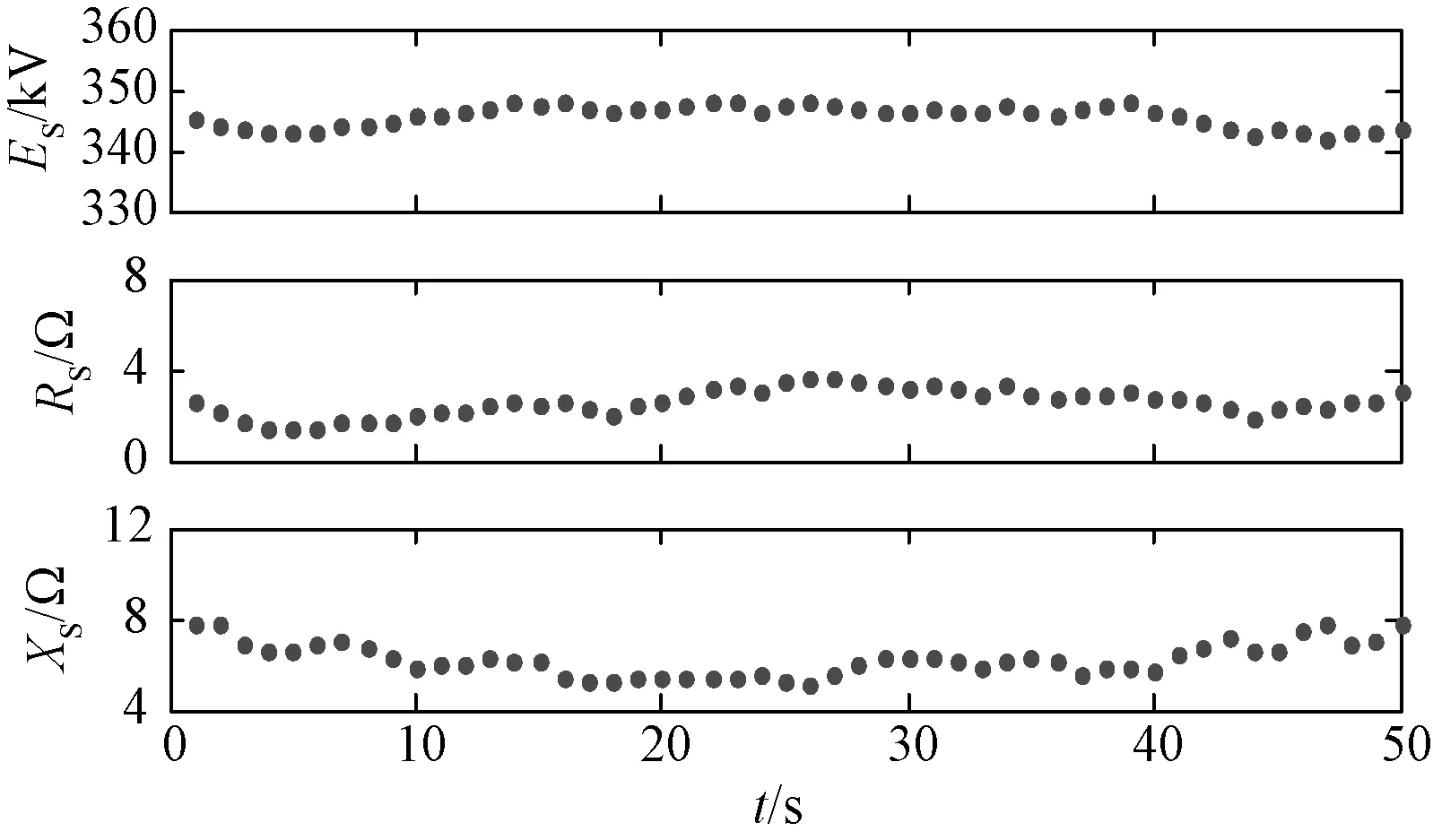
图11 5次谐波系统参数估计值Fig.11 5th hamonic system parameters estimation
表5 5次谐波系统参数估计均值(50s)
Tab.5 Estimation of 5thharmonic system parameters mean value (50s)

ES/Vδ/(°)RS/ΩXS/Ω变电站1345.76-22.912.586.24变电站2350.53-20.552.797.38变电站3349.26-21.372.447.06变电站4345.01-25.622.916.73
5.4 基波正序波动系数取值参考
波动系数是数据选择指标中的关键参数,是根据数据波动特性计算得到的,对系统参数估计精度有着直接影响,因此研究其波动系数具有一定的意义。波动系数k1、k2、k3分别对应系统电压、负荷电阻和负荷电抗。定义波动系数目的是初步选出系统侧基本不变而负荷侧存在波动的数据,结合文中第4节所提出的波动率,通过大量数据分析可知,当k1、k2、k3对应的波动率区间分别为0~0.4%、1.2%~2.0%、0.2%~0.6%时,所选数据基本符合算法估计要求。基于本文所用的14.4kV变电站的多组采样数据,分别根据以上波动率区间计算其波动系数,结果如表6所示。

表6 基波正序波动系数Tab.6 Fundamental positive sequence fluctuation factor
由表6可知,各组数据的波动系数k1、k2、k3的取值范围大约为0.40~0.44、0.35~0.37、0.32~0.38,在同一电压等级下,由波动率区间计算出的波动系数取值相差不大,具有较强的规律性。以上所述研究思路也可拓展至其他电压等级的系统,针对不同的电压等级,可根据该波动率区间计算波动系数,避免同一电压等级下波动系数的反复计算,提高参数估计的运算效率。
6 数据选择方法的估算结果对比
对于非干预法,有效地处理PCC点测量数据所含噪声与奇异值的干扰是精确估计系统等值参数的关键。文献[23]基于变电站实测数据,采用高斯-牛顿法求解计算系统戴维南等值参数。对于数据中存在的噪声与干扰,文献[23]提出“判别式法”对实测数据进行筛选。该方法主要原理如下:首先对方程式(9)左右两边取平方并将上下两式相加,然后代入三组PCC点的电压和电流数据,整理可得:
(22)
方程组式(22)中共有ES、RS、XS三个未知量,对其进行整理可以消掉ES、XS,得到一个关于RS的一元二次方程。当Δ≥0(Δ=b2-4ac,ax2+bx+c=0)时,该方程组有实数解。图12和图13给出了利用本文所提的数据选择方法和利用文献[23]所使用的判别式法进行参数估计的结果,其中图12为变电站1的基波正序阻抗估计结果,图13为5次谐波阻抗的估计结果。
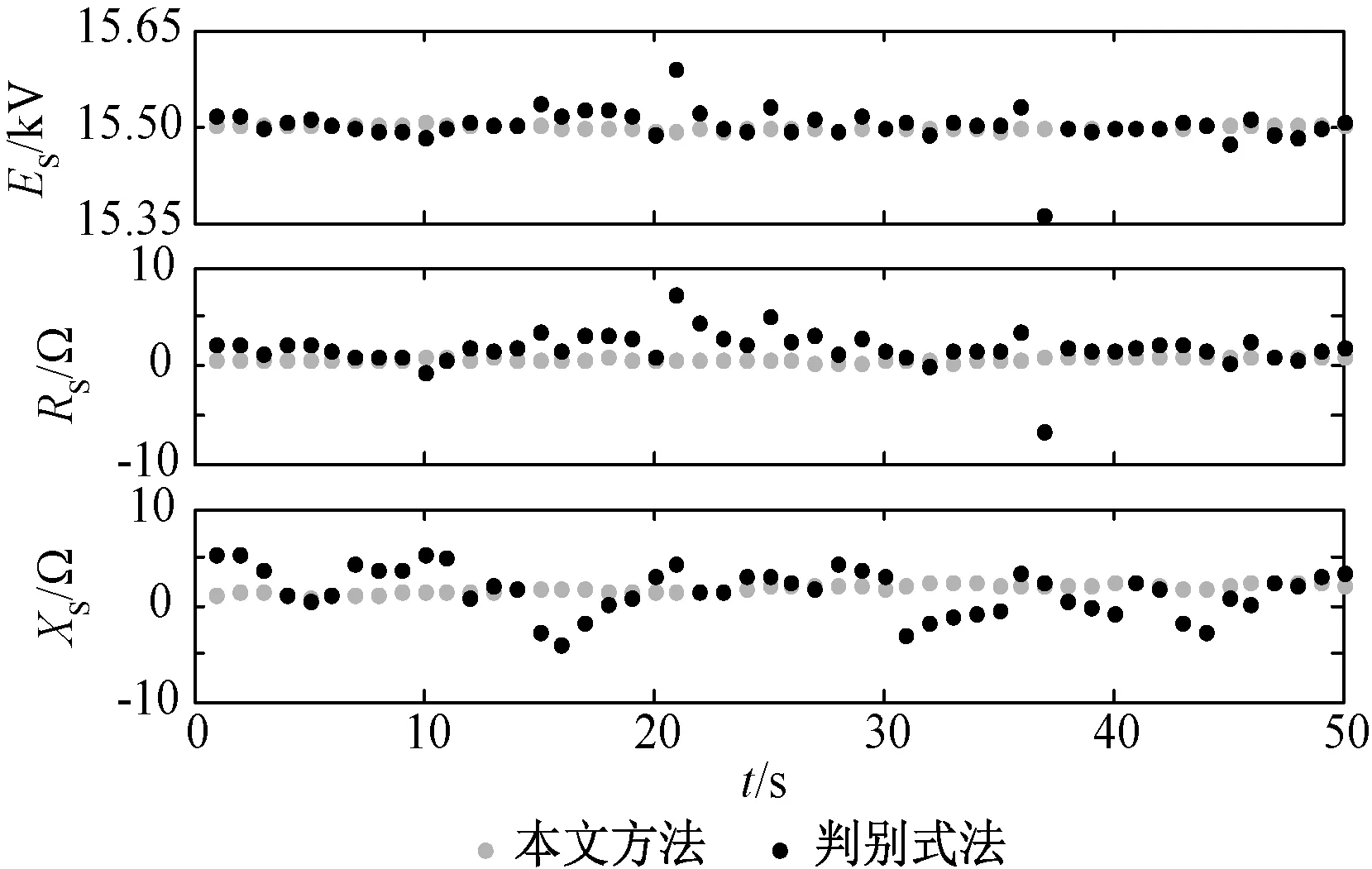
图12 基波正序参数估计结果比较Fig.12 Fundamental positive sequence parameters comparison

图13 5次谐波参数估计结果比较Fig.13 5th harmonic system parameters comparison
可见,判别式法的估计结果波动较大,且存在不合理的异常值,而本文所提方法的系统参数估计结果没有异常值。主要原因是判别式法仅考虑到实测数据是否有实数解,未考虑系统阻抗的估计精度,所以该方法筛选后的系统参数估计结果误差较大。同时由于判别式法在对数据进行筛选的过程中要对一元二次方程是否有实解进行判定,相比本文所使用的回归估计法要复杂,因此计算时间也要长。算例分析结果也验证了这点。本文所用的实测数据1s采样6个周波,50s的采样数据作为一组进行系统参数估计,因此每组数据共包含300个采样周波,计算中对1s内的估计结果取平均值作为该时刻系统参数估计值。研究表明,判别法处理一组实测数据的处理时长大约为3min,而本文方法约为1.5min。因此本文所使用的方法在数据处理所需时间上也优于判别式法。
7 结论
本文提出了基于偏最小二乘回归法估计系统侧的戴维南等值参数的方法,该方法将等值参数的求解转换为计算回归模型中的回归系数,抑制了稳态时系统自然波动对参数估计的影响,对PCC点的数据进行了有效辨识;结合变电站母线的实测数据分析,提出了能够选择出系统侧基本保持恒定而负荷侧有较大波动的数据筛选指标;基于多个变电站的实测数据,对其正序、负序以及谐波等值电路的参数进行了估计,验证了本文所提方法的有效性。文中进一步根据各变电站的参数估计结果,总结了基波正序分量筛选指标中关键参数的取值规律,为实际应用提供了一定的参考价值。下一步将针对噪声干扰研究相应的辨识方法,进一步提高谐波和负序系统等值电路参数的估计精度。
[1] Y Wang, C Wang, F Lin, et al. Incorporating generator equivalent model into voltage stability analysis [J]. IEEE Transactions on Power Systems, 2013, 28 (4): 4857-4866.
[2] Milosevic B, Begovic M. Voltage-stability protection and control using a wide-area network of phasor measurements [J]. IEEE Transactions on Power Systems, 2003, 18 (1): 121-127.
[3] 颜伟, 文一宇, 余娟, 等 (Yan Wei, Wen Yiyu, Yu Juan, et al.). 基于戴维南等值的静态电压稳定广域切负荷控制策略 (A wide-area load shedding strategy based on Thevenin equivalence and considering static voltage stability) [J]. 电网技术 (Power System Technology), 2011, 35 (8): 88-92.
[4] 刘文霞,吴方权 (Liu Wenxia, Wu Fangquan). 风场群接入系统的静态电压稳定分析 (Static voltage stability analysis of power systems with wind farm groups) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2014, 33 (6): 13-17.
[5] Kim I, Aggarwal R.K. A study on the on-line measurement of transmission line impedances for improved relaying protection [J]. International Journal of Electrical Power & Energy Systems, 2006, 28 (6): 359-366.
[6] C S Indulkar, K Ramalingam. Estimation of transmission line parameters from measurements [J]. Electrical Power and Energy Systems, 2008, 30(5): 337-342.
[7] L He, C Liu. Parameter identification with PMUs for instability detection in power systems with HVDC integrated offshore wind energy [J]. IEEE Transactions on Power Systems, 2014, 29 (2): 775-784.
[8] M Ciobotaru, V Agelidis, R Teodorescu. Line impedance estimation using model based identification technique[A]. Proceedings of the 2011 - 14th European Conference on Power Electronics and Applications (EPE 2011) [C]. 2011. 1-9.
[9] R Langella, A Testa. A new method for statistical assessment of the system harmonic impedance and of the background voltage distortion [A]. 9th International Conference on Probabilistic Methods Applied to Power Systems[C]. Stockholm, Sweden, 2006. 1-7.
[10] 刘秀玲, 王洪瑞 (Liu Xiuling, Wang Hongrui). 电网谐波阻抗的测量及其修正(Measurement and correction of network harmonic impedances) [J]. 电力系统及其自动化学报 (Proceedings of the CSU-EPSA), 2007, 19 (2): 55-59.
[11] 王诗超, 沈沉, 李洋, 等 (Wang Shichao, Shen Chen, Li Yang, et al.). 基于波动量法的系统侧谐波阻抗幅值估计精度评价方法 (A fluctuation quantity based method to evaluate estimation precision of harmonic impedance amplitude at system side) [J]. 电网技术 (Power System Technology), 2012, 36 (5): 145-149.
[12] F Giuseppe, L Arturo, R Mario. Constrained Least Squares Methods for parameter tracking of power system steady-state equivalent circuits [J]. IEEE Transactions on Power Delivery, 2000, 15 (3): 1073-1080.
[13] 康婕, 解绍峰, 刘晓菊, 等 (Kang Jie, Xie Shaofeng, Liu Xiaoju, et al.). 基于支持向量基的谐波阻抗估计方法 (Assessing the harmonic impedance based on support vector machine) [J]. 电力系统保护与控制 (Power System Protection and Control), 2010, 38 (22): 131-135.
[14] 蒋文林, 郭玉恒, 薛东江, 等 (Jiang Wenlin, Guo Yuheng, Xue Dongjiang, et al.). 基于小波的畸变波形同步分层谐波阻抗估计 (Assessing harmonic impedance by synchronously delaminated distortion waves based on wavelet) [J]. 电力自动化设备 (Electric Power Automation Equipment), 2005, 25 (2): 33-36.
[15] A Yakov, H Jing, A Keith, et al. New techniques for measuring impedance characteristics of three-phase AC power systems [J]. IEEE Transactions on Power Electronics, 2009, 24 (7): 1802-1810.
[16] 马丽叶, 卢志刚, 刘佳, 等 (Ma Liye, Lu Zhigang, Liu Jia, et al.). 计及负荷不确定性的电网参数分析和优化 (Analysis and optimization of network parameters considering load uncertainty) [J].电网技术 (Power System Technology),2012, 36 (12): 146-152.
[17] 张付生, 汪鸿,韩悌,等 (Zhang Fusheng, Wang Hong, Han Ti, et al.). 基于偏最小二乘回归分析的短期负荷预测(Short-term load forecasting based on partial least-squares regression) [J]. 电网技术 (Power System Technology),2003,27 (3):36-40.
[18] 王惠文(Wang Huiwen). 偏最小二乘回归方法及其应用(Partial least-squares regression - Method and applications) [M]. 北京:国防工业出版社(Beijing: National Defend Industry Press),1998.
[19] 华回春,贾秀芳,张韶光 (Hua Huichun, Jia Xiufang, Zhang Shaoguang). 谐波责任定量评估的邻域多点测量方法 (Neighborhood multi-point measurement method for harmonic contribution determination) [J]. 电网技术 (Power System Technology), 2014, 38 (2): 502-508.
[20] GB 4883-1985, 数据的统计处理和解释 - 正态样本异常值的判断和处理(Statistic interpretation of data - Detection and handling of outlying observation in normal sample) [S].
[21] 高海翔,王小宇,刘锋,等 (Gao Haixiang, Wang Xiaoyu, Liu Feng, et al.). 未来电网运行形态研究 (Operation morphology design for future power grids) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2014, 33 (1): 58-65.
[22] 吴晓梅,缪希仁 (Wu Xiaomei, Miao Xiren). 低压系统多层级短路故障早期检测辨识研究 (Research on early detection of short-circuit fault in multi-level low voltage system) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2015, 34 (9): 38-43.
[23] S A Arefifar, W Xu. Online tracking of power system impedance parameters and field experiences [J]. IEEE Transactions on Power Delivery, 2009, 24 (4): 1781-1788.
Thevenin equivalent circuit parameter estimation analysis for PCC upstream system
ZHANG Kun1, DAI Chuan-kai2, SUN Yuan-yuan1, YIN Zhi-ming3
(1. School of Electrical Engineering, Shandong University, Jinan 250061, China; 2. State Grid Weifang Electric Power Company, Weifang 261021, China; 3. State Grid Training Center of Beijing Electric Power Company, Beijing 100041, China)
The accurate estimation of the Thevenin equivalent circuit parameters for the PCC upstream systems is of great importance to the power system security and stability analysis. Based on the Thevenin equivalent circuit model, firstly, the paper pointed out that the main challenge for the system equivalent circuit parameter estimation is to overcome the impact of the synchronous variations of the system side and load side parameters. Then the partial least square method is applied to establish the regression equations in order to acquire the parameters of the system side equivalent source and impedance. Moreover, through the analysis of the fluctuation probability of the PCC voltages and the load impedance based on the measured substation data, new data selection indices are proposed in order to improve the accuracy of parameter estimation. With the help of the indices, the constant system data and the considerable variation load data can be selected out. Simultaneously the variation laws for the data selection indices are further analyzed. Based on the method proposed, the Thevenin equivalent circuit parameters for the system side under the positive sequence, negative sequence and harmonic conditions can be estimated efficiently. And the practical examples analysis verifies the validity of the method.
Thevenin equivalent circuit parameter; partial least square; data selection; fundamental frequency component; harmonics
2016-04-28
国家自然科学基金项目(51577108)、 山东省优秀中青年科学家科研奖励基金项目(BS2013NJ005)
张 坤(1989-), 男, 山东籍, 硕士研究生, 研究方向为电能质量分析; 戴传凯(1990-), 男, 山东籍, 助理工程师, 硕士, 研究方向为电能质量分析。
TM74
A
1003-3076(2017)04-0007-09

