优化教学方式 促进整体发展
谢小丽
在初中数学教学过程中,我们发现,学生的学习效果有明显的差异。有的学生能够妥善应对各个知识模块的出现与变化,而有的学生便显得有些力不从心,甚至陷入了基础不牢又要面对新知识,因而继续“基础不牢”的恶性循环。在具体教学中,教师除了要关注学习能力较强学生的学习状态,更要把精力多投注在学习有困难的学生身上。这部分学生的学习状态好坏,才能体现数学教学水平的高低,更关乎整个班级学习水平的提升与否。因此,教师有必要从全体学生现状着眼,找到适合整体发展的教学方式。
一、营造和谐学习氛围,激发学生学习兴趣
想要强化班级学习有困难学生的学习效果,最根本的是要将这部分学生的学习兴趣激发起来,让他们从心里爱上数学。因此,在课堂上营造出一个和谐的学习氛围,是促进他们发展的第一步。想要实现这个教学效果有很多种途径,教师可以根据当前教学内容的特点分别运用。
例如,在开始对方程内容进行教学之前,我先向学生展示了这样一个问题:某服装制造厂共有24名工人,专门负责制作同一品牌的运动服和运动裤,每人每天可以完成3件运动服或5件运动裤的制作。(1)为了让制作出来的运动服和运动裤能够配套,应当怎样对工人进行安排,才能够使得每天制作出的运动服与运动裤的数量相等?(2)若每件运动服可以产生收益30元,每件运动裤可以产生收益16元,为了让该服装制造厂每天可以产生不低于2100元的收益,最少需要多少工人来制作运动服?这种贴合实际生活的问题,很快吸引了学生的注意力,并让大家在寻找答案的兴趣当中,产生了对方程知识的学习期待。接下来的教学也就得以顺利地展开了。
初中阶段的学生仍然比较喜好新鲜生动的事物,想要将他们的关注热情激发起来,并不是一件困难的事情。教师们只要注意观察学生的喜好,并能够将之巧妙融入课堂教学的设计当中去,就能让学生对数学知识的学习产生兴趣。如果能够在课堂教学开端便将这种积极的氛围营造出来,自然可以为学生的整体知识学习奠定心理基础。
二、积极总结学习规律,提高学生学习效率
面对数量繁多的知识内容,学习效率止步不前也是让很多初中学生感到困惑的地方。学习效率无法提升,一方面,会让学生投入更多的学习精力,增大课业负担;另一方面,收获的学习效果与投入的学习精力不成正比,也会严重削弱学生的学习自信,造成学习困难。因此,教师一定要想办法从提高学习效率的角度对学困生提供帮助。
例如,在学习对角平分线的内容时,学生遇到了这样一道题目:如下图所示,∠AOB是直角,∠BOC为30°,OM和ON分别是∠AOC和∠BOC的角平分线。(1)∠MON的大小是多少?(2)如果∠AOB的大小为α,其他条件没有变化,则∠MON的大小是多少?(3)如果(2)中∠BOC的大小为β,其他条件没有变化,则∠MON的大小是多少?(4)从上述三个问题的思考当中,你能总结出什么规律呢?在这个问题中,多条角平分线和多个角穿插在一起,让很多学生感到思路十分凌乱。然而,具体到这道题目的解答当中,并不是那么复杂的。思维的关键在于以整体的眼光来看待其中的关键角,并以角平分线所分出的相等角加以替换,实现最终求解,并不需要将每一个角的大小分别求出。就此,我带领学生总结出了整体的规律方法,明显简化了思维过程。
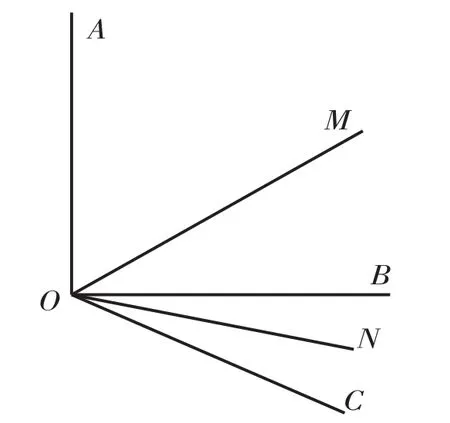
想要准确快捷地完成数学学习,只靠用蛮力是不行的,最重要的是要从中找到规律和方法。这就像是解决数学学习问题的一把万能钥匙,握住了它,就可以在面对诸多类似模式的不同问题时普遍适用。如此一来,学生只需要掌握几种固定的思想方法,便可以有效处理数量庞大的数学问题。这显然能够让初中数学学习事半功倍。
三、巧妙拓展学习形式,激发学生学习自觉
数学学习活动,说到底还是学生自己的事。无论教师一方如何下力气,如果学生没有从内心产生接受知识的愿望,学习效果仍然不会理想。因此,将学生的主观学习能动性激发出来,也是从根本上扭转相对落后学生的学习现状的有效途径。让学生产生学习自觉性的方法有很多,拓展课堂教学中的学习形式是很有效的一种。
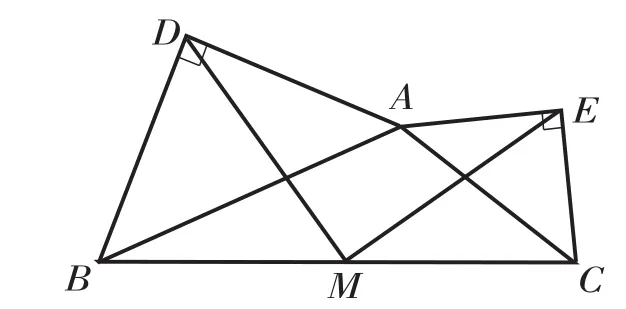
例如,在教学三角形的基本性质时,为了调动学生的思维积极性,我设计了这样几个教学步骤进行灵活拓展:(1)如右图一所示,在△ABC中,AB=AC,分别以这两条边为斜边向该三角形的外侧做等腰直角三角形,DF⊥AB于F,EG⊥AC于G,M是BC中点,连结MD、ME,则在结论“AB=2AF=2AG”“MD=ME”“此图呈轴对称”“MD⊥ME”中,哪些是正确的?(2)如右图二所示,以任意三角形中的AB与AC边为斜边,向其外侧做等腰直角三角形,M是BC中点,连结MD、ME,则MD与ME之间有何关系?(3)如右图三所示,以任意三角形中的AB与AC边为斜边,向其内侧做等腰直角三角形,M是BC中点,连结MD、ME,则△MEC是何种三角形?从基础知识出发的连续拓展提问,紧紧抓住了学生的思维节奏,并让大家十分乐于投入到这种逐步深入的思考当中。

(图一)
(图二)
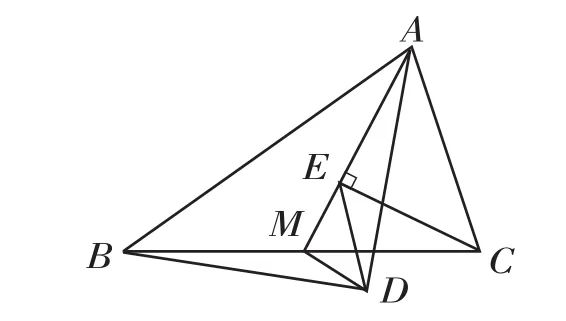
(图三)
通过丰富课堂上的教学形式,学生不仅感受到了数学学习的乐趣,更在亲身参与知识探究的同时,体验到数学方法产生于运用的真实触感。几次训练下来,学生逐步迈入了条理化思维的轨道,并初步建立起了独立分析数学问题的自信,将数学学习作为自己的主动意愿。如此一来,学困生在整个学习过程中的角色已经开始向主动转变了。
四、适时查找学习疏漏,完善学生学习体系
当然,造成学生学习困难的一个关键原因还在于知识掌握过程当中出现的漏洞过多。这就如同被蝼蚁侵蚀的大坝,如果漏洞太多,大坝自身的建造体积再大也无济于事。因此,想要完善学困生的学习体系,还应适时查找并填补学习过程当中的疏漏之处。
例如,为了强化学生对于直角三角形概念与性质的理解,我给出了如下四个条件:(1)某三角形的三条边长之比为;(2)某三角形的三条边长之比为1∶2∶3;(3)某三角形的三个内角度数之比为3∶4∶5;(4)某三角形一条边上的中线是这条边长的一半。在这四个条件所描述的三角形中,哪些是直角三角形?学生原本认为自己已经将直角三角形的知识掌握到位了,但经过这个问题的考察,发现了许多自己并未发现的知识细节。这正是知识学习的弱点所在。发现了这些疏漏之后,学生很自觉地开始回头重温直角三角形的基本内容,意识到了夯实知识基础的重要性。
学习漏洞的产生不可避免,重要的是我们能不能及时发现并妥善处理好这些漏洞。特别是对于学困生来讲,更需要教师从旁协助引导,帮助他们发现学习当中出现的薄弱环节,并带领他们加以纠正,强化学习成效。
在初中数学教学中,教师要做到“首尾兼顾”,既要重视班级中领头学生的能力提升,更要关注学困生。造成学生学习困难的原因有很多,想要促进学困生发展,切入点也是很多的。只有从影响学习效果的多个方面同步入手,才能从根本上完善学困生知识体系的建立,最终推动数学教学效果稳步提升。

