基于随机森林的异步电动机转子断条故障诊断
史干东,吴文军,张玉鸿,史丽萍
(1.中国矿业大学,徐州 221008;2.国网四川省电力公司,成都 610041)
0 引 言
异步电动机转子断条故障是常见电机故障之一,它将导致电动机运行性能下降,严重时电机会因此无法驱动负载而出现堵转、停转,甚至烧坏电机,威胁工业生产的可靠性和安全性,同时增加生产成本[1]。因此对该故障及早进行检测和诊断颇为重要。
基于定子电流特性分析是异步电动机转子断条故障在线诊断的常用方法。研究表明,定子电流中包含电机的故障特征,因而通过提取定子电流故障特征可以准确地检测电机故障[2]。例如当异步电动机定子电流中出现(1+2s)f1频率分量(f1为供电频率,即定子电流基频分量,s为转差率)时,电机则发生转子断条故障,因此在判断转子断条故障时可以以该边频分量作为特征向量[3]。
在异步电动机转子断条故障检测中,FFT是最常用的电流特性分析方法。但是当电机负载比较小时,转差率s非常低,边频分量(1+2s)f1极其接近基频f1,同时边频分量的幅值较基频很小且由于噪声干扰,这就导致边频分量极易被淹没,频谱泄露在所难免,此时基于FFT的定子电流特征分量提取方法的灵敏度便会大打折扣[4]。
为此,文献[4]使用混合骨干微粒群优化算法获得基波参数后构造出基波表达式,并将其从原始信号中剔除,以突出故障特征频率成分,但此方法过程繁琐,计算量大;文献[5]采用Hilbert变换把基波成分转换成直流信号从而使故障特征更加明显,但存在交叉项问题。
目前神经网络[6-7]、支持向量机[8-9]等为电机状态识别主流方法。神经网络具有自适应学习能力,但是其在样本训练时容易陷入局部最优,同时支持向量机也存在训练速度较慢的问题,尤其是故障特征量较多时,该方法占用系统较多资源,不利于在线故障诊断。不仅如此,以上两种方法都只是基于单一分类器的故障诊断方法,因而正确率较低。
本文针对异步电动机转子断条故障诊断中的故障特征量提取和故障识别问题,首先采用Park矢量模平方函数方法提取转子断条时的故障特征量,然后以其作为输入量训练随机森林形成分类器群,识别故障模式,以实现异步电动机转子断条故障的准确诊断。
1 Park矢量模平方函数
当异步电动机转子发生断条故障时,定子电流中会出现边频分量fbb=(1+2ks)f1(为简化起见,令k=1),故定子三相电流(ia,ib,ic)可以用下列形式表达[10],即:
ia=Ifcos(ωt-α)+Idlcos[(1-2s)ωt-βl]+
Idrcos[(1+2s)ωt-βr]
(1)
ib=Ifcos(ωt-α-2π/3)+
Idlcos[(1-2s)ωt-βl-2π/3]+
Idrcos[(1+2s)ωt-βr-2π/3]
(2)
ic=Ifcos(ωt-α+2π/3)+
Idlcos[(1-2s)ωt-βl+2π/3]+
Idrcos[(1+2s)ωt-βr+2π/3]
(3)
式中:If,α为基波电流f1的幅值、初相位;Idl,βl为左边频分量(1-2s)f1的幅值、初相位;Idr,βr为右边频分量(1+2s)f1的幅值、初相位。
将式(1)、式(2)和式(3)代入式(4)和式(5),则Park矢量的两个分量变为[11]:
idlcos[(1-2s)ωt-βl]+
idrcos[(1+2s)ωt-βr]}
(4)

idlsin[(1-2s)ωt-βl]+
idrsin[(1+2s)ωt-βr]}
(5)
Park矢量模平方函数:
3ifidlcos(2sωt-α+βl)+
3ifidrcos(2sωt+α-βr)+
3idlidrcos(4sωt+βl-βr)
(6)
因此,Park矢量模平方函数含有的成分:一个直流分量,两个频率分别为2sf1和4sf1的交流分量。其中,4sf1频率分量为最高频率分量。该方法可以凸显故障特征,能够很好地将边频交流分量与电源基频分量区分开来,消除传统基于FFT的电机电流频谱分析方法的一些局限性。
2 特征量提取
故障特征的准确提取是运用随机森林算法进行异步电动机故障识别的关键之一。以Park矢量模平方函数方法提取故障特征时,断条故障特征频率2sf1和4sf1远离基频而靠近0,故能避免边频分量“湮没”问题。同时为避免电机气隙偏心对故障识别正确率的影响,将0~20 Hz频段作为断条故障模式识别的特征频段。然后对0~20 Hz频段进行量化处理(量化单位1 Hz),得到20个量化值。其具体方法参考文献[11]。然后用式(6)中的直流分量去除这20个量化值进行“归一化”处理,并将此结果作为异步电动机转子断条故障的特征矢量,亦即随机森林的输入量。图1为异步电动机在正常情况和转子断条故障下的A相定子电流波形,图2、图3分别为电机正常状态和断条故障时的特征矢量。
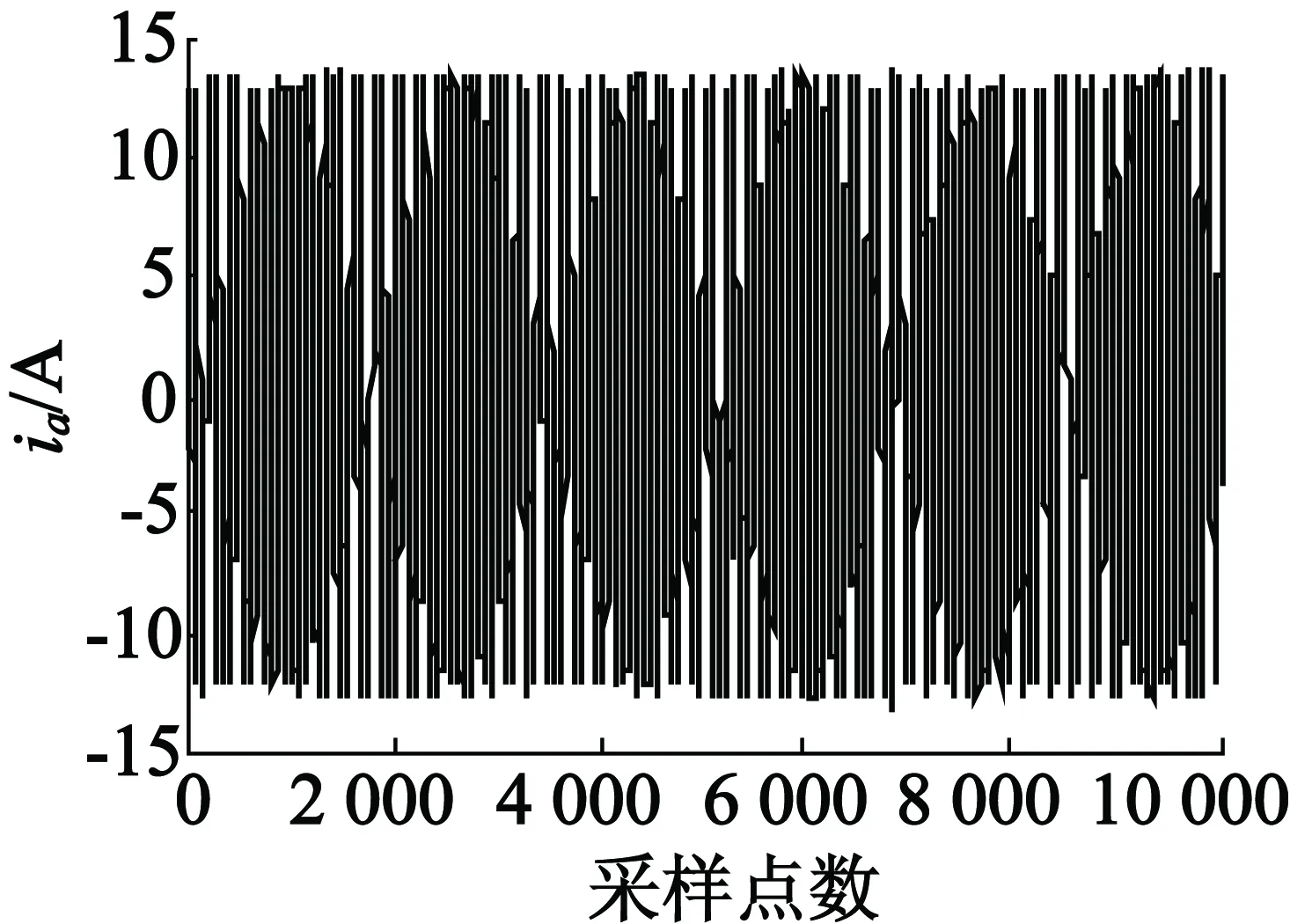
(a) 正常电机
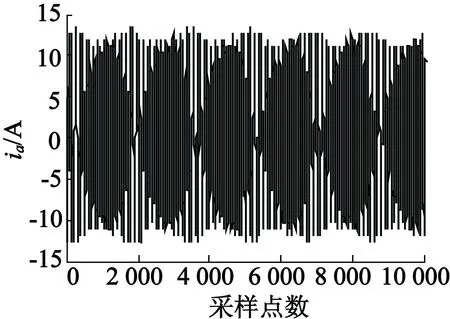
(b) 转子断条故障

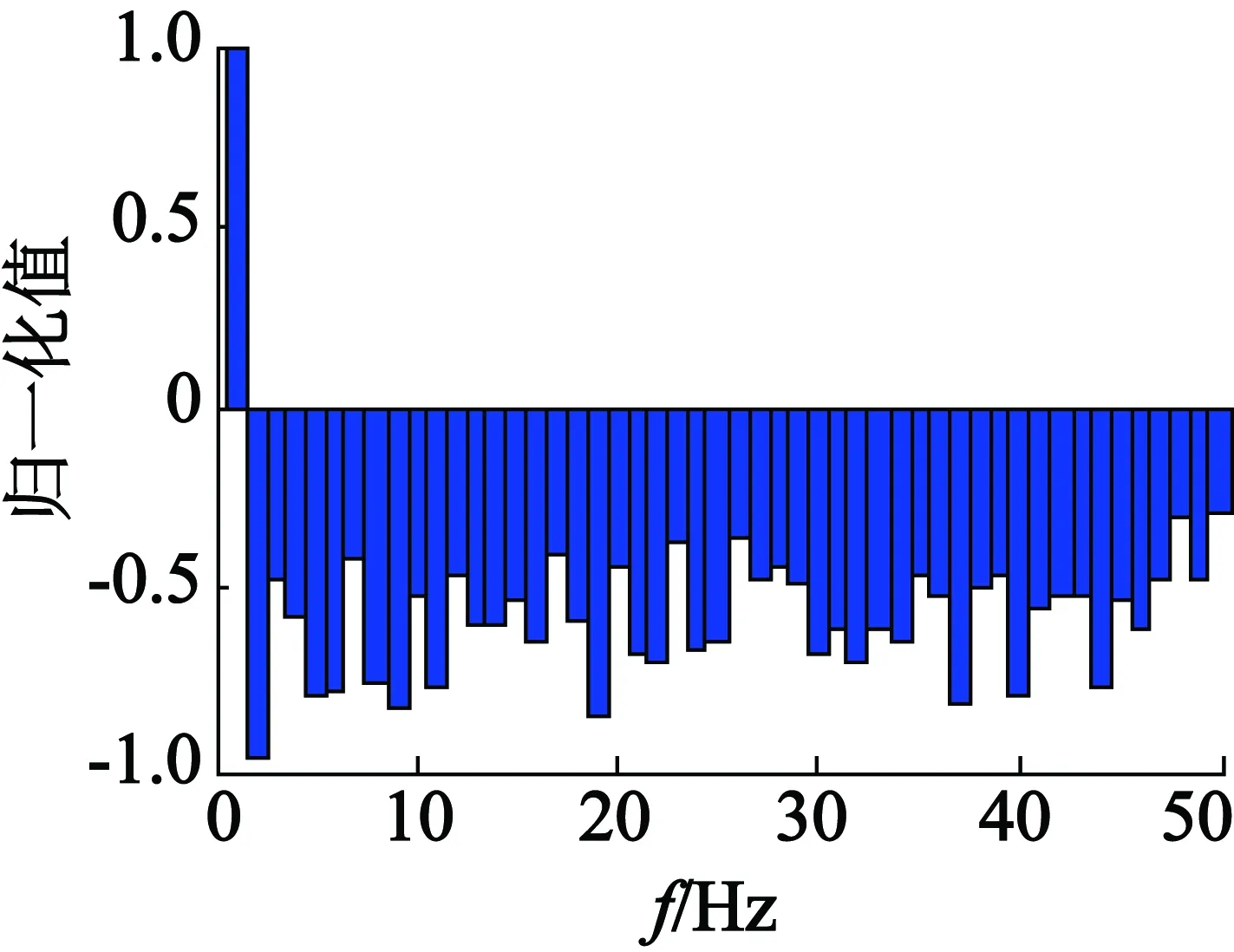
图2 正常电机特征矢量

3 随机森林算法
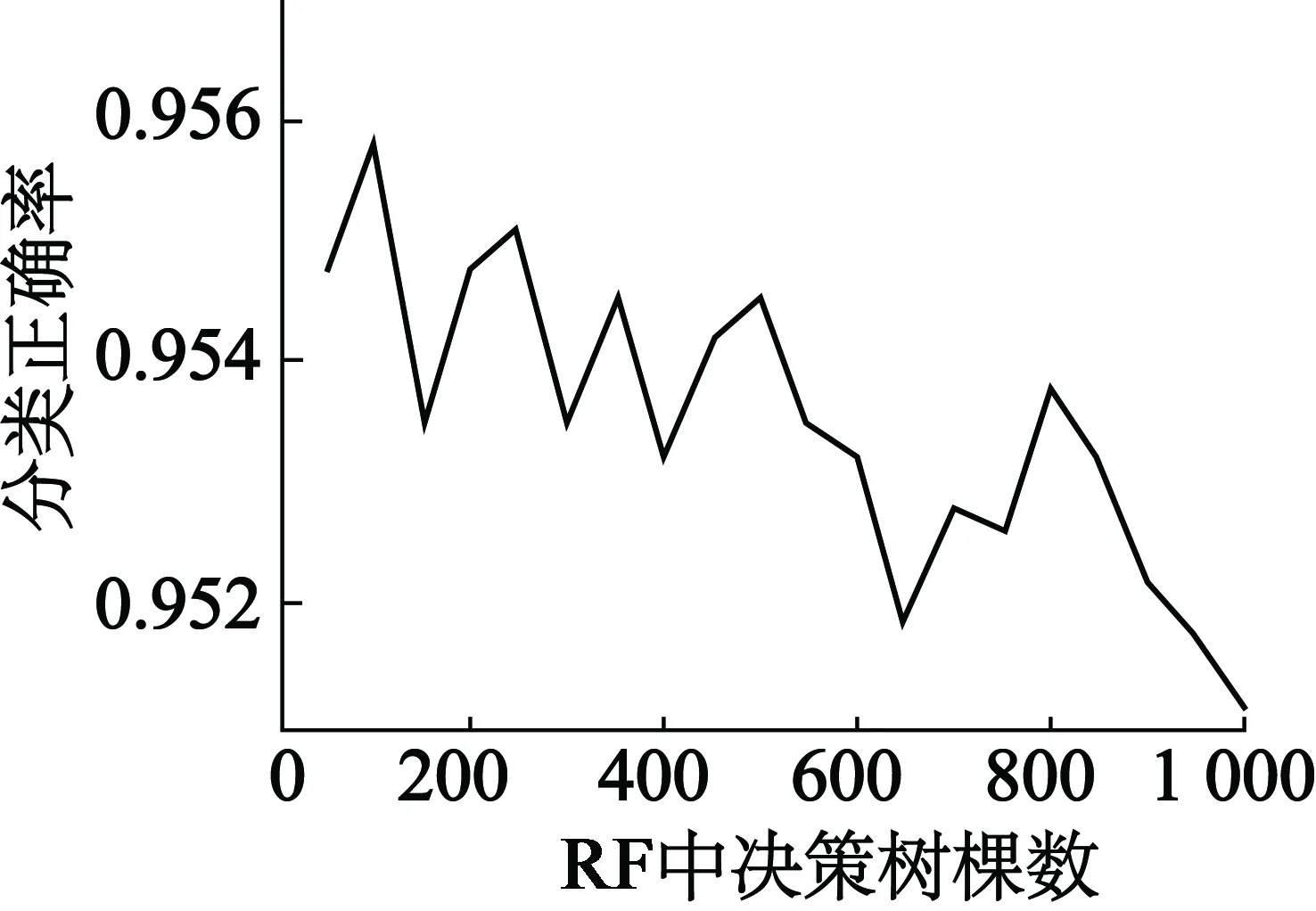
随机森林(以下简称RF)算法[12]结合了Breimans的“Boot Strap Aggregating”思想和H.O.的“random subspace”方法[13]。该方法的实质是一个分类器群,即包含了多棵决策树的分类器,所有决策树随机形成,从而形成RF,森林中的树之间没有关联。诊断时,将测试数据输入RF,然后让每一棵决策树独自进行诊断分类,即“投票”,最后综合投票结果,将所有决策树中分类结果最多的那类为最终结果。RF的步骤如下[14](设样本的特征值个数为M,且0 1) 自助重采样。从训练数据集中采用有放回采样的方法,随机抽取k个样本(k为决策树的数目),形成新的训练样本集,具体方法参考文献[15]。 2) 决策树生成。利用自助重采样得到的k个训练样本集创建对应的单棵决策树。单棵决策树的生成方法:从M个特征值中随机选取m个特征值作为当前节点的分裂特征集,然后根据节点不纯度最小的原则对该节点进行分裂。 3) 为使每个节点不纯度最小,对单棵决策树不进行剪枝,保证其完整生长。 4) 投票。对于测试数据集,利用单棵决策树进行测试,得到对应的类别,从而RF得到多个结果。然后采用“投票”的方法,将单个决策树中输出类别最多的结果作为测试数据集的最终所属类别。 RF中决策树的数量对分类器的性能影响很大,本文确定RF中包含决策树数量为100。 图4为该文所提方法的整个流程图。 图4 转子断条故障诊断方案 实验电机为一台Y132M-4型感应电机,其主要技术参数如表1所示。 表1 实验电机主要技术参数 选取具有代表性的正常电机(故障类别为0)和断条故障(故障类别为1)的三相电流数据各150组,按照上述的方法提取特征矢量,组成训练数据集,创建RF。另外再选取40组正常电机和30组断条故障电机三相电流数据,提取特征矢量,作为测试数据集。其中,30组断条故障电机数据为转子断条1根情况下,分别以电机轻载、半载和满载时,在不同时间节点各取10组数据,然后提取特征矢量组成测试数据。由于电机在轻载、半载和满载时特征频率2sf1和4sf1均在0~20 Hz频段以内,故电机在额定负载转矩以内运行时不会影响特征矢量的提取,本文的方法有效。图5为测试数据集的混淆矩阵。 图5 混淆矩阵 由图5可以看出,在测试集的70个样本中,一共有3个样本被判断错误(1个正常状态被错判为故障状态,2个故障状态被错判为正常状态),总的正确率为95.7%。当训练样本增加的时候,RF的正确识别率还有一定的提高。这表明RF用于异步电动机断条故障诊断具有良好的性能。 另外,为了便于比较,本文同时采用相同的数据集训练BP神经网络,形成故障诊断模型。神经网络输入层节点数为20,隐含层节点数为10,输出层节点数为2。训练中,学习率设为0.05,目标误差为0.000 04。将测试数据集输入创建的BP神经网络,其结果如表2所示。 表2 不同识别方法的性能比较 表2结果说明:与BP神经网络相比,RF具有更高的正确识别率,且缩短了训练和分类时间,为电机在线故障诊断提供可能,因而具有更好的实用价值和市场前景。 RF中决策树的棵数对算法的泛化能力具有较大影响,因此合理确定树的棵数对故障识别的准确率至关重要。为了分析决策树棵数对算法性能的影响,作如下处理:确定决策树棵数以后,创建100个RF模型,取所有森林准确率的平均值作为当前决策树棵数下的分类准确率,从而降低了随机性的影响。图6为不同决策树棵数对电机故障正确识别率的影响。由图6易知,当RF所含决策树数目在100左右时算法性能最佳,且此时也有利于缩短程序运行时间,为异步电动机断条故障的在线诊断提供可能。 图6 决策树棵数对算法性能的影响 本文首先利用Park矢量模平方函数方法使异步电动机转子断条故障特征频率远离基频,便于故障特征量的凸显及准确提取。然后再利用RF自动识别电机断条与否。RF因为包含了多棵决策树,不仅增加了其泛化能力,也进一步提高了故障识别的准确率。同时,RF算法简单,在训练过程中无需耗费大量时间用于参数搜索和优化,降低了计算量。与传统的BP神经网络、支持向量机等方法相比,该方法缩短了训练时间,提高了故障识别的正确率,避免了传统方法在模型建立时的随机性、盲目性。实例验证表明,该方法用于异步电动机转子断条故障诊断具有良好的性能,取得较好的效果。 [1] 刘振兴,尹项根,张哲,等.基于瞬时功率信号频谱分析的鼠笼式异步电动机转子故障在线诊断方法[J].中国电机工程学报,2003,23(10):148-152. [2] 马宏忠,胡虔生,黄允凯,等.感应电机转子绕组故障仿真与实验研究[J].中国电机工程学报,2003,23(4):107-112. [3] DELEROI W,DELEROI W.Broken bar in a squirrel-cage rotor of an induction motor[J].1984,67(3):141-149. [4] 王攀攀,史丽萍,张勇,等.采用一种混合骨干微粒群优化算法的感应电机转子断条故障诊断[J].中国电机工程学报,2012,32(30):73-81. [5] 马宏忠,姚华阳,黎华敏.基于Hilbert模量频谱分析的异步电机转子断条故障研究[J].电机与控制学报,2009,13(3):371-376. [6] 管春,周雒维,卢伟国.基于多标签RBF神经网络的电能质量复合扰动分类方法[J].电工技术学报,2011,26(8):198-204. [7] 王红君,刘冬生,岳有军.基于小波分析和神经网络的电机故障诊断方法研究[J].天津大学学报,2009,40(1):69-73. [8] 魏于凡.支持向量机在智能故障诊断中的应用研究[D].北京:华北电力大学,2007. [9] 杨俊燕,张优云,赵荣珍.支持向量机在机械设备振动信号趋势预测中的应用[J].西安交通大学学报,2005,39(9):950-953. [10] 侯新国,吴正国,夏立.基于Park矢量模平方函数的异步电动机转子故障检测方法研究[J].中国电机工程学报,2003,23(9):137-140. [11] 张建文.电气设备故障诊断技术[M].北京:水利水电出版社,2006:154-160. [12] RANDOM L B.Random forests[J].Machine Learning,2001,45(1):5-32. [13] HO T K.Random subspace method for constructing decision trees[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,1998,20(8):832-844. [14] 王小川.MATLAB神经网络43个案例分析[M].北京:北京航空航天大学出版社,2016:256-264. [15] BREIMAN L.Bagging predictors[J].Machine Learning,1996,24(2):123-140.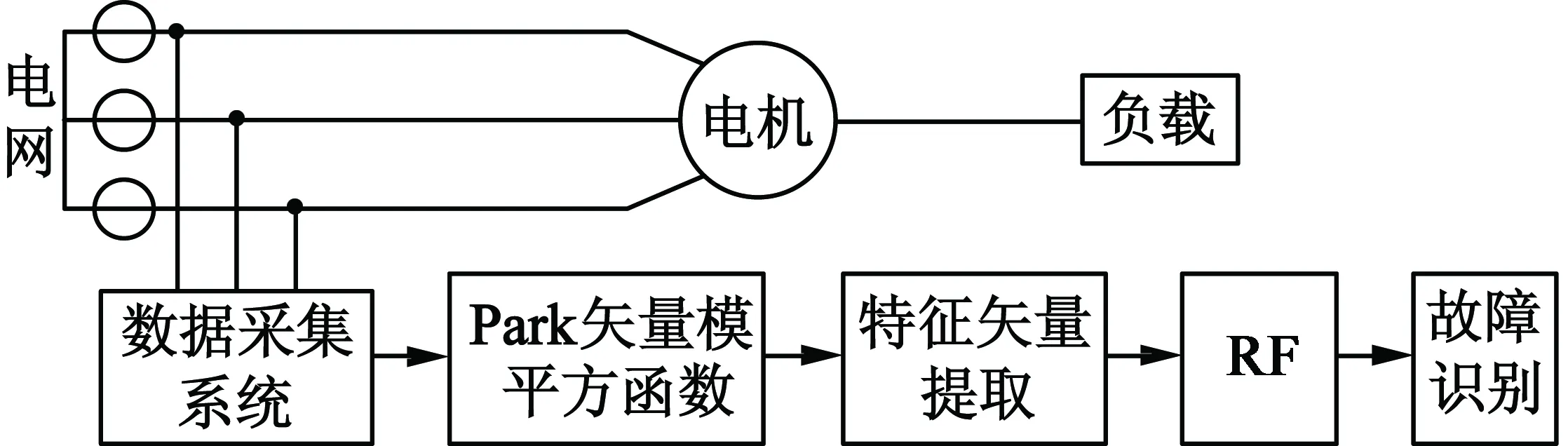
4 实例验证



5 RF算法性能分析
6 结 语

