装甲装备贵重、低消耗可修复备件两级库存配置建模与仿真
(1. 陆军装甲兵学院装备保障与再制造系, 北京 100072; 2. 61377 部队, 广东 深圳 518017)
可修复备件是指通过采用经济可行的技术手段可恢复原有功能的备件[1]。随着装备的升级换代和部队换件修理的广泛展开,在装甲装备保障费用中,价格昂贵而又不经常消耗的可修复备件所占比重越来越大[2]。该类备件通常在装备战斗力生成过程中发挥着关键作用,且一般生产周期较长,因而需预先储备一定数量的库存;但由于其价格昂贵且技术含量高,过量储备既费财力又易因积压而失效。通过完善贵重可修复备件保障机制,使故障件得以及时修复和有效再利用,对降低备件库存数量、节约备件保障经费、提高备件保障效率和效益具有重要意义。
与不可修复备件相比,可修复备件涉及故障件的回收与修复等,因此,其库存控制问题更为复杂。SHERBROOKE[3]最早提出的METRIC(Multi-Echelon Technique for Recoverable Item Control)模型是可修复备件库存控制的理论基础,应用十分广泛。罗祎等[4]基于该模型建立了三级库存体系的备件配置模型;阮旻智等[5]增加了备件体积和质量约束,建立了面向任务的舰船携行备件配置模型;聂涛等[6]研究了该模型在K-N冗余雷达系统备件供应优化中的应用。然而,上述研究在建模时均基于“无限修复能力”这一假设,即故障件在修复时不存在排队等待的情况,这会导致模型计算结果出现一定误差。因此,文献[7-9]作者放宽了无限修复能力假设,基于排队论对METRIC模型进行了修正,但大都只考虑了有限修复能力对“在修复数量”这一随机变量均值的影响,而未考虑对其方差的影响。另外,上述研究成果大都假设备件完全修复、不存在报废,且多以装备使用可用度作为保障效能评价指标,不符合装甲装备保障实际,也未通过有效的方法对模型的准确性进行验证。
为了解决上述问题,笔者对装甲装备贵重、低消耗可修复备件的“基地-部队”两级供应保障机制进行描述;综合考虑有限维修渠道、报废率等因素,建立备件配置模型,并运用边际分析法进行求解。最后,通过算例分析验证模型的可信性和有效性。
1 备件保障机制描述
根据经济订货批量模型(Economic Ordering Quantity,EOQ),采取(s,S)库存策略时年度费用CT(包括产品价格费用、订货费用和库存持有费用)的计算公式为
(1)
式中:D为产品年需求量;CP为产品单价;Q为每次订货批量;CO为每次订货固定费用;H为单位产品年库存持有费用(通常设定为产品单价CP与常数k的乘积)。对式(1)求Q的导数,并令其为0,得到年度费用最低时的最佳订货批量
(2)
图1为EOQ模型中产品最佳订货批量,反映了CO=0.5,k=0.1时,Q*随D和CP变化的趋势。可以看出:当D< 2件且CP> 2万元时,Q*值会接近于1。也就是说,当产品价格很高、消耗率很低时,每消耗1件备件就需要1次订货。结合可修复备件保障实际,每当换件修理消耗1件库存,应立即向上级申请1件补给,同时,上交故障件进行修复。这种方式可最大限度地减少可修复备件库存配置数量,降低保障费用,同时,缩短故障件的修复周期,提高可修复备件的利用率。

图1 EOQ模型中产品最佳订货批量
根据上述分析,装甲装备贵重、低消耗可修复件的“基地-部队”两级保障运行机制如图2所示。

图2 装甲装备贵重、低消耗可修复件两级保障机制
基地级保障机构由基地仓库和基地维修机构组成,部队级保障机构由部队仓库和部队维修机构组成。当部队装备发生故障,定位到故障部件后,若故障比较简单,则可借助厂家直修、战区巡修或部队检修等形式进行现场快速修复;否则,从部队仓库中调拨备件进行换件维修,若库存量为0,则等待库存补给到达后再进行换件维修。从装备上拆下的故障件上交基地仓库,同时向基地仓库申请1件备件。基地仓库接到申请后,从本级仓库中调拨1件备件供应该部队仓库,若库存数量为0,则等待库存补给到达后再行供应。基地仓库接到故障件后,根据修复能力和修复范围,分为战区修理大队、大修工厂或生产厂家3种情况进行修复,修复后的备件存入基地仓库;若不能修复,则该故障件报废,由基地仓库向厂家订购1件新品以维持整体库存水平。
2 备件库存配置建模
Palm定理是METRIC模型的理论基础,它假设故障件的修理时间相互独立,即维修机构具有无限的修复能力,故障件修复时不需要排队等待。然而,在实际工作中,当故障件修复时间较长时,忽略排队等待时间,会明显低估备件短缺量,从而影响模型的准确性。因此,笔者引入M/M/c排队模型,在有限修复能力下,建立考虑报废率的可修复件库存配置模型。
2.1 模型假设
为便于分析和计算,首先对备件保障过程作如下假设:
1) 每次装备功能失效都是由单一部件故障引起的;
2) 基层各项备件需求相互独立,均服从稳态泊松分布;
3) 故障件立即送修,且修复如新;
4)修复故障件所需子级备件充足,无短缺;
5)不存在串件拼修和横向调剂供应。
2.2 模型构建
在“基地-部队”两级保障机制下,部队备件满足率取决于备件库存配置数量和待接收备件数量。设某基地下的部队仓库数为I,对某型装甲装备共J项可修复备件进行库存配置,则在有限修复能力下,部队仓库i(i=1, 2,…,I)的第j(j=1, 2,…,J)项备件某一时刻的待接收数量Xij由以下2部分构成:
(3)
式中:λij和rij分别为部队仓库i的第j项备件的故障率和现场可修复概率;Oi为部队仓库i从发出备件申请到接收备件的时间。
基地仓库第j项备件的需求率为
(4)
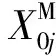
(5)
(6)

(7)
(8)
(9)
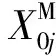
(10)
综合式(7)、(8)、(10)可知:X0j的均值和方差分别为
(11)
(12)
记Pr(x0j)为X0j的概率分布,根据常见的离散分布统计特性,若D(X0j)/E(X0j)≈1,则Pr(x0j)选择泊松分布;若D(X0j)/E(X0j)>1,则Pr(x0j)选择负二项分布;若D(X0j)/E(X0j)<1,则Pr(x0j)选择二项分布。若基地仓库第j项备件库存配置数量为S0j,则其短缺数B(S0j)的均值和方差分别为
(13)
D[B(S0j)]=E[B2(S0j)]-E2[B(S0j)],
(14)
(15)

(16)
fij2D[B(S0j)]。
(17)
式中:fij=λij(1-rij)/λ0j,为基地仓库第j项备件需求量中来自部队仓库i的备件所占比例。
综合式(3)、(16)、(17),Xij的均值和方差分别为
(18)
(19)
记Pr(xij)为Xij的概率分布,同样可根据常见的离散分布统计特性确定其分布类型。
目前,常见的可修复备件库存配置模型大都以装备使用可用度作为备件保障效能评价指标。但我军装甲装备在动用过程中遵循“滚动式循环动用”原则,并根据摩托小时储备将装备分为战备车和教练车,其中教练车又分为控制用车、一般用车和重点用车。各类装备实行区别动用和战教轮换,重点用车动用频繁,易发生故障;战备车和控制用车基本不动用,装备完好性较好。因此,利用装备使用可用度来衡量所有装备的可用性是不合理的。
针对这一情况,笔者选用备件满足率作为备件保障效能评价指标。备件满足率是指需要备件时不缺件的概率[10],可根据备件库存配置数量和供应渠道概率分布计算得出。若部队仓库i第j项备件库存配置数量为Sij,则其备件满足率为
(20)
进一步可得系统备件满足率为
(21)
一般情况下,备件库存配置建模的目标是在满足规定的备件满足率的前提下,使备件库存配置费用最低。因此,备件配置模型可描述为
(22)
式中:C为备件配置费用;cj为第j项备件的单价;φ为设定的保障效能指标最低值。
3 模型求解
边际分析法是求解METRIC模型最常用的方法。与遗传算法等群智能优化算法相比,边际分析法过程简单、结果稳定,不会丢失最优解,在解空间规模不是特别大的情况下非常适用。因此,笔者选用该方法来求解模型。
式(22)中的决策变量为记录基地和部队仓库各项备件库存量的(I+1)×J维矩阵
(23)
该模型的边际分析法求解过程如下:
1) 初始化决策变量S=0。
2) 通过不断地迭代执行边际分析(在每次迭代过程中,遍历决策变量矩阵的每个位置),依次计算其边际效益值
(24)
式中:O为与S结构相同且第i行第j列值为1、其他位置为0的0-1矩阵。
3) 将最大的边际效益值max(Δij)所对应的决策变量S中位置Sij的值加1,即Sij=Sij+ 1。
4) 根据式(21)计算系统备件满足率F,若F≥φ,则停止迭代,决策变量S所表示的方案即为最优备件配置方案;否则,返回步骤2),继续迭代。
4 备件保障过程仿真
通过仿真对装甲装备贵重、低消耗可修复备件两级供应保障过程进行动态模拟,统计相关保障效能指标,并与模型计算结果进行比较,验证模型的准确性和可行性。基于Agent的建模与仿真(Agent-Based Modeling and Simulation,ABMS)方法是随着分布式人工智能技术的发展而逐渐兴起的一种建模技术。其中Agent是系统仿真模型的基本组成单元,可理解为具有自治性、社会性、主动性和反应性等智能特征的个体,能够适应环境变化,并主动执行任务[11]。ABMS通过Agent之间、Agent与环境之间的交互和协作,可更加真实地还原系统的结构和运行情况,因而被广泛地应用于复杂系统建模与仿真研究中。“基地-部队”两级保障机制下备件保障过程仿真Agent的层次结构如图3所示。
ABMS是一种典型的面向对象的建模仿真方法,因而面向对象方法中的分析、设计与实现技术都可被借鉴到ABMS中,如统一建模语言(Unified Modeling Language,UML)等[12]。时序图是UML动态模型图之一,与Petri网等形式化语言相比,它可更加直观地展示系统中Agent间交互行为发生的先后顺序以及触发交互行为的事件或消息。备件保障过程仿真Agent时序图如图4所示。

图3 “基地-部队”两级保障机制下备件 保障过程仿真Agent的层次结构
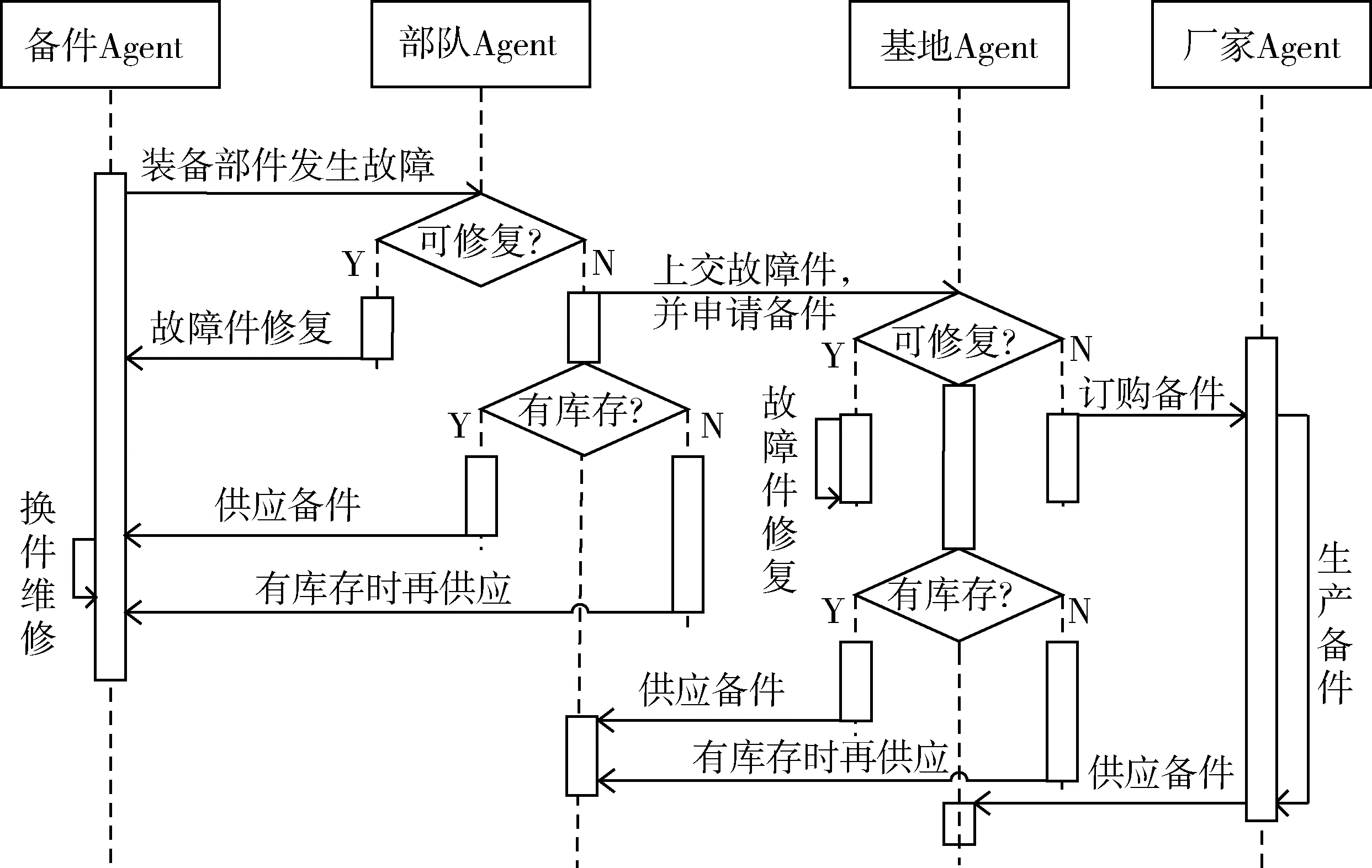
图4 备件保障过程仿真Agent时序图
5 算例分析
5.1 算例求解
现对由Z战区及其下属2个旅(1旅和2旅)组成的两级备件供应保障系统进行库存配置。2个旅向Z战区申请备件所需时间分别为O1=0.04 a,O2=0.08 a。某型装备在2个旅的列装数量均为50台,该型装备的中小修用备件约有1 000项,从中选取来自4个子系统的12项需求率低、价格高的可修复备件进行库存配置,其参数设置如表1所示。
设定φ=0.90,运行边际分析法求解模型,经过91次迭代后,得到备件最佳库存配置优化结果及备件满足率如表2所示,系统备件满足率F=0.904,备件配置费用C=309.4万元。由库存配置结果可以看出:各项备件均以战区集中储存为主,旅基本不储或少量储存。与各旅分散储存相比,战区集中储存的备件可供各旅共同使用,因而以更少的备件实现相同的保障效果。
为了分析有限修复能力对库存配置模型准确性的影响,利用标准VARI-METRIC模型[3]和文献[1]的修正模型,分别计算1旅(i=1)的备件库存配置方案对应的备件满足率,结果如表3所示。可以看出:不考虑修复能力的影响会高估备件满足率;且与文献[1]模型相比,本文的库存配置模型对有限修复能力影响的修正效果更加明显。

表1 备件参数设置
注:时间单位为年(a);价格单位为万元。

表2 备件库存配置优化结果

表3 1旅仓库备件满足率F1j对比
5.2 仿真验证
Anylogic是一款新兴的、基于JAVA语言的系统建模仿真平台,同时支持离散事件系统建模、系统动力学建模、基于Agent的建模等多种建模方式;提供了友好的可视化界面,通过简单的编程即可实现复杂的逻辑功能;支持普通仿真、蒙特卡罗仿真、优化仿真、比较运行、敏感性分析等多种仿真实验。因此,笔者选择Anylogic平台对第5.1节算例进行仿真。仿真系统框架如图5所示。

图5 仿真系统框架
部队备件满足率是本文库存配置模型的核心指标,故将其作为检验模型准确性的统计变量。根据定义,备件满足率为备件库存数量不小于0的时间与仿真运行时间之比。在Anylogic中设置2种实验类型进行仿真:
1) 设置实验类型为普通仿真,观察备件保障过程中各项系统指标的实时变化情况。设仿真时间单位为月,即每秒推进1个月。在仿真过程中,1旅仓库前3项备件(j=1,2,3)的库存数量和备件满足率的实时变化情况分别如图6、7所示。可以看出:每当备件发生短缺时,其满足率随即变小。

图6 1旅仓库备件库存数量实时变化曲线
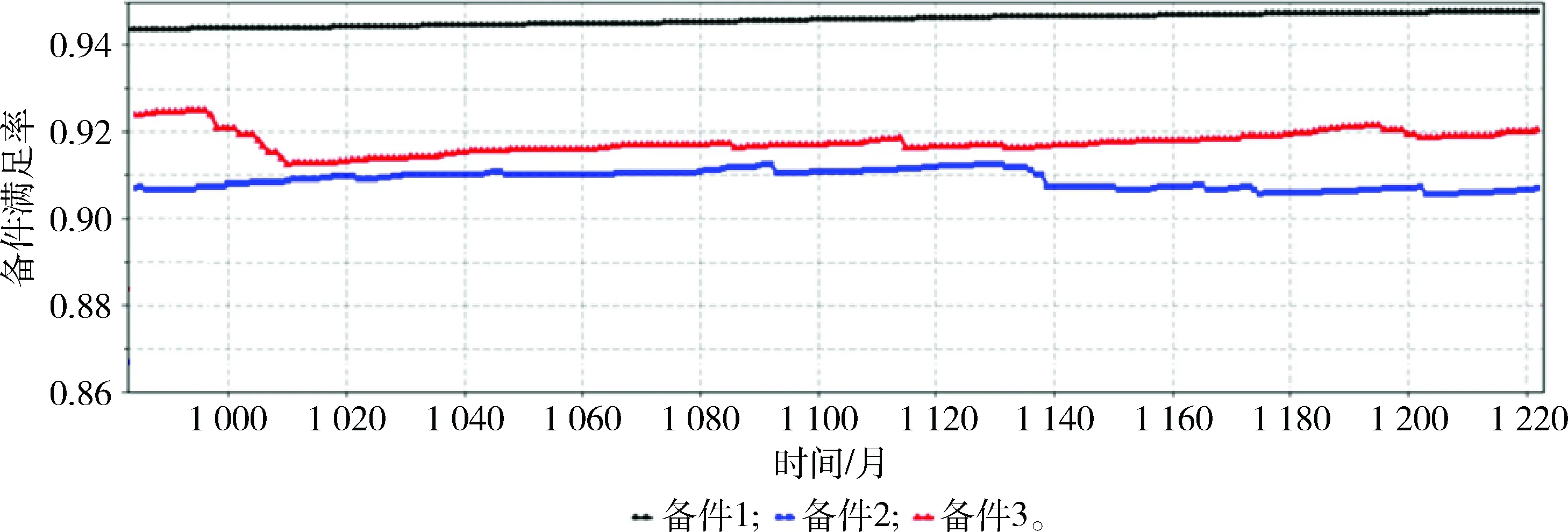
图7 1旅仓库备件满足率实时变化曲线
2) 设置实验类型为蒙特卡罗仿真,验证模型准确性。设置仿真次数为100次,每次仿真运行周期P=1 200月;为了消除初始状态对系统指标的影响,只对后1 000个月进行统计分析。分别统计2个指标的仿真样本均值和标准差,利用终止型序贯程序法[13]得到置信度为90%的置信区间,如表4所示。

表4 仿真样本统计分析结果
将仿真得到的置信区间与表2、3中模型计算的备件满足率进行对比可知:模型计算结果都落在了置信区间内,且与标准VARI-METRIC模型和文献[1]模型计算结果相比,本文提出的库存配置模型的计算结果更接近仿真样本均值。
6 结论
笔者以装甲装备贵重、低消耗可修复备件为研究对象,综合考虑报废率、有限修复能力等因素,建立了两级库存配置模型,设计了模型的求解算法,并通过仿真验证了模型的可信性和有效性。通过研究发现:对于该类备件,应以基地仓库集中储存为主,部队仓库基本不储或少量储存;且修复能力的有限性对该类备件库存配置模型的可信性和有效性有一定的影响,在建模时应予以考虑。本文的研究成果对提高装甲装备备件保障效益、完善备件保障机制具有一定的参考意义。
参考文献:
[1] 张帅,李军亮,吕卫民,等.有限维修能力下舰载机可修复件库存优化模型[J].北京航空航天大学学报,2015,41(6):1034-1041.
[2] 王慎,李庆民,王文斌,等.面向两级可修复备件库存系统的动态管理模型[J].计算机集成制造系统,2015,21(3):788-799.
[3] SHERBROOKE C C.Optimal inventory modeling of system: multi-echelon techniques [M].2nd ed.Boston:Artch House,2004:35-42.
[4] 罗祎,阮旻智,袁志勇.多级维修供应下可修复备件库存建模与优化[J].系统工程理论与实践,2013,33(10):2623-2630.
[5] 阮旻智,傅健,周亮,等.面向任务的作战单元携行备件配置优化方法研究[J].兵工学报,2017,38(6):1178-1185.
[6] 聂涛,盛文.K:N系统可修复备件两级供应保障优化研究[J].系统工程与电子技术,2010,32(7):1452-1455.
[7] LAU H C,SONG H.Multi-echelon repairable item inventory system with limited repair capacity under non-stationary demands [J].International journal of inventory research,2008,1(1):67-92.
[8] 徐立,李庆民,胡毅钧,等.有限维修能力下多级保障系统装备时变可用度评估及保障方案优化[J].国防科技大学学报,2017,39(1):128-136.
[9] YOON H, JUNG S, LEE S.The effect analysis of multi-echelon inventory models considering demand rate uncertainty and limited maintenance capacity [J].International journal of operational research, 2015, 24(1):38-58.
[10] 张志华,应新雅,费广玉.串联系统备件满足率分配及配置优化[J].系统工程理论与实践,2015,35(11):2987-2992.
[11] 白金鹏,李天.面向指标论证的战斗机突防效能评估[J].航空学报,2016,37(1):122-132.
[12] 李雄,蒲玮,唐亚林.基于UML的战时装备维修保障行动建模研究[J].计算机测量与控制,2016,24(1):143-145.
[13] 隽志才,孙宝凤.物流系统仿真[M].北京:电子工业出版社,2007:166-168.

