四色定理的简单证明

曹晟

【摘要】四色定理的本质就是在平面或者球面上无法构造五个或者五个以上两两相连的区域，通过对问题的逻辑思维抽象，可以在二维空间内证明.而对四色定理本身的研究，也会因不同的思维模式促进新思想理论的产生，进而推进数学事业的发展.

【关键词】四色；三角形；拓扑

一、四色定理思考过程

四色定理作为世界数学三大猜想之一，于1976年6月，在美国伊利诺斯大学的两台不同的电子计算机上，用了1200个小时，作了100亿判断，结果没有一张地图是需要五色的，最终证明了四色定理，轰动了世界.

但是这种证明并不是一位数学爱好者真正想要的，这个问题本身不应该用到这么复杂的计算手段，而是存在一种简单的书面证明，可以以一种直观、便于交流的方式去体现四色定理的正确性.同时，我一直认为利用图形来解决这个问题是最好的方法，也是最简单的方法，随后我做了如下思考：能否脱离地图本身的限制，将地图上各个区域之间的逻辑关系在另一个二维平面内展现出来？

对此，我进行了如下的逻辑抽象变换：

1.将地图上不同的区域用不同的点来表示.

2.点与点之间的连线用来表示地图上两区域之间的相邻逻辑关系，所以，线与线之间不可交叉，否则就超越了二维平面，而这种平面我们可以暂时称它为逻辑平面，它只反应区域之间的关系，并不反应实际位置.

通过以上的变换处理，可以将对无穷尽的实际位置的讨论，变为有条理、可归纳的逻辑关系的讨论，从而提供了简单书面证明的可行性.

二、四色定理证明过程

现在设有一对相邻区域A和B，若染色，只需A，B两种颜色即可，但若想用到第三种颜色，则需要在二维平面内画出另一区域，使其同时与A，B两区域相邻，如图1.

这种情况使用了A，B，C三种颜色，且必须要用三种颜色，同理，若想用到第四种颜色，就必须创造出第四个区域使其在二维平面内同时与A，B，C三个区域相邻，如图2.

这个地图一共使用了四种颜色，那么是否可以用到第五种颜色还需进一步讨论.现在，我要用以下两步把这个图形抽象出来.

当平面内只有A，B这两个相邻区域时，可如图3表示.

此时只需A，B两种颜色.若必须用到第三种颜色时，创造C点，必须同时与A，B相连，如图4.

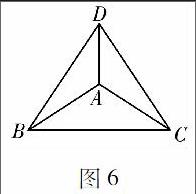
现在二维平面被△ABC分成了两部分，若必须用到第四种颜色时，需在△ABC内或△ABC外找一点D，使之同时与A，B，C三点相连，且不可相交.如图5、图6.

图5图6

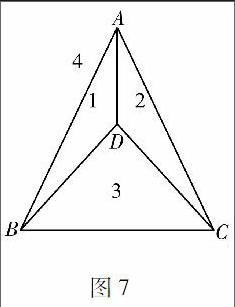
图7可以看出，当点D与A，B，C三点相连时，虽然D点所处区域不同，但A，B，C，D四个点的点线关系结构并未发生变化.

上面这个图形的点线关系，代表了所有必须要用到四种颜色的地图的最简关系，换句话说，也就是所有必须要用到四种颜色的地图，都可以抽象出这个结构图形，我们暂且称它为四色分割三角形.

现在，这个图形将二维平面分成了1，2，3，4四个区域，接下来讨论第5个点E的情况，若想用到第五种颜色，则必须使点E同时与A，B，C，D四个点相连，且不可以交叉，那么根据区域的不同，只存在以下四种情况.

1.点E处在1区域时，由于限定条件，E点只能与A，B，D三点相连，那么，可以用C点颜色来涂E，不需要第5种颜色.

2.点E处在2区域时，由于限定条件，E点只能与A，C，D三点相连，那么，可以用B点颜色来涂E，不需要第5种颜色.

3.點E处在3区域时，由于限定条件，E点只能与B，C，D三点相连，那么，可以用A点颜色来涂E，不需要第5种颜色.

4.点E处在4区域时，由于限定条件，E点只能与A，B，C三点相连，那么，可以用D点颜色来涂E，不需要第5种颜色.

综上所述，在二维平面内不存在点E可以构造五个或者五个以上两两相连的区域.